Passive Morphological Adaptation for Obstacle Avoidance in a Self-Growing Robot Produced by Additive Manufacturing

Abstract

This article presents strategies for the passive path and morphological adaptation of a plant-inspired growing robot that can build its own body by an additive manufacturing process. By exploiting the soft state of the thermoplastic material used by the robot to build its structure, we analyzed the ability of the robot to change its direction of growth without the need for specific cognition and control processes. Obstacle avoidance is computed by the mechanics from the body–environment interaction. The robot can passively adapt its body to flat obstacles with an inclination of up to 50° with resulting reaction forces of up to ∼10 N. The robot also successfully performs penetration and body adaptation (with 30° obstacle inclination) in artificial soil and in a rough unstructured environment. This approach is founded on observing plant roots and how they move and passively adapt to obstacles in soil before they actively respond followed by cell division-based growth.

Introduction

Underground penetration and exploration technologies have a long history and can be exploited in many sectors, such as agriculture, for example, to define soil water content¹; geology, for example, for terrain seismic profiling² and underground characterization³; and the oil and gas industry⁴ or construction, for example, for mapping and maintenance of underground utility service infrastructures⁵ and tunneling.⁶

Autonomous solutions, which can monitor the surrounding environment, make decisions, and adjust their behavior for improving penetration and exploration, could help make the process faster, more reliable, cheaper, and safer for humans and underground infrastructures.⁷ However, robotic solutions for such applications are still very limited,^8–13 due to the strong constraints imposed on the movement of autonomous systems below ground by the physics of such a cluttered environment (i.e., high pressure and friction, stratifications with different soil impedance, and rocks).

Ideally, a robotic system moving in soil should be able to adapt its actions to unpredictable constraints, avoiding or navigating around obstacles or sensitive objects, for example, to prevent damaging underground pipes or objects of the cultural heritage. However, they have a limited possibility of perception compared to aboveground robots, which for instance can take advantage of vision. Thus, within the soil, a possible strategy for movement and exploration is for the morphology of the body to adapt itself to the soil structure.

Morphological adaptation in artificial solutions has been particularly exploited in the field of soft-bodied robotic systems,^14,15 where soft materials are adopted for the deformation of soft artificial bodies, for moving through small gates^16,17 or navigating cluttered environments, for example, by exploiting the passive buckling ability of soft inflatable structures in a robot, without the use of a sensory perception or bending control.¹⁸ Material properties or soft actuators are used for enhancing robot abilities.¹⁹ In fact, the adaptation provided by soft materials and actuators can effectively improve robot behaviors while decreasing the control complexity.^20,21 The exploitation of morphological adaptation in soft robotics is often grounded on the observation of soft-bodied animals²² and plants,²³ considering the importance of body–environment interaction for robot design and control.^24,25

For soil penetration and exploration, plant roots can be used as a model to design and develop new technological solutions.²⁶ To survive, plants have to carefully and efficiently direct their growth mediating different environmental cues,^27–29 while mechanically interacting with the environment³⁰ and negotiating obstacles.³¹ For instance, experiments have shown that, in the presence of obstacles, plant roots partially inhibit other stimuli (e.g., gravity) as a strategy to follow the surface of the barrier and get round the obstacle.³² The active response to obstacles, that is, impeded soil or barriers, is called thigmotropism, which is mediated by specific transients of Ca²⁺ signals triggered when the root is mechanically stimulated, thereby obtaining the repulsive directed growth.³³ Plants adopt several strategies to manage hard soil and overcome obstacles. Growth from the root tip is one of these strategies since the cell division and elongation at the apical level help reducing the lateral friction required to move in soil.³⁴ However, the active differential growth is anticipated by a passive cell wall deformation in the root tip, which is induced by a mechanical perturbation.³⁰ Additionally, the adaptation to mechanical stimulation can be enabled by buckling and radial expansion. Buckling consists of a passive bending below the mature region of the root,³⁵ obtained in thin roots that grow in weak soil medium when they meet a stronger soil medium. This passive bending might help finding a new way to avoid obstacles.³⁶ Radial expansion happens in root tip, together with a decrease of cell elongation, to help in propagating cracks in extremely hard soil.^37,38

On the basis of our observations of plant roots, in previous works, we proposed autonomous artificial robots for soil penetration³⁴ and exploratory activities.³⁹ Our self-growing robot grows by the addition of new material at its tip, thus drawing inspiration from the growth strategy of plants. We implemented this strategy by integrating a customized three-dimensional (3D) printer-like mechanism in the robotic root and using a thermoplastic filament (polylactic acid [PLA]) as a structural material.¹³ The robot grows through an additive manufacturing process, which results in a miniature system that tunnels through the soil. The PLA changes its viscoelastic properties when heated and becomes soft and malleable above 150° so that it can be molded.⁴⁰ Controlled differential deposition of a thermoplastic material at the opposite sides of the body enables the robot to bend in any direction.^13,41 These works focused mainly on the design and development of a 3D printer root-like robot and on active control strategies for material deposition. Moreover, the bioinspired control implemented in the previous version imitates the active tropism-based strategies of plant roots, mediated by sensory feedback.³⁹

The present work focuses on the ability of our plant root-like robot to imitate the passive behavior and morphological adaptation of a natural root while growing. Specifically, we demonstrate that the robot can avoid obstacles by exploiting the PLA behavior at high temperatures, without the use of a specific sensory perception or a bending control.

The main goals of this article are to (1) understand how the interaction with the surrounding environment can contribute to passively shaping the robot body exploiting a few seconds of the material malleability and (2) characterize this behavior by isolating the contribution in adaptation induced by body material properties from other possible yet complementary contributions (e.g., tip shape and material).

This capability contributes to enhancing the compliance of the robot with the environment, facilitating soil penetration with a passive adjustment of the direction of growth (e.g., to avoid underground infrastructures), while simplifying its movement control.

In the Growing Robot section, we introduce our self-growing robot. In the Experimental Protocol section, we describe the experimental protocol and give the results in the Results and Discussions section. The conclusions are drawn in the Conclusions section.

Materials and Methods

Growing robot

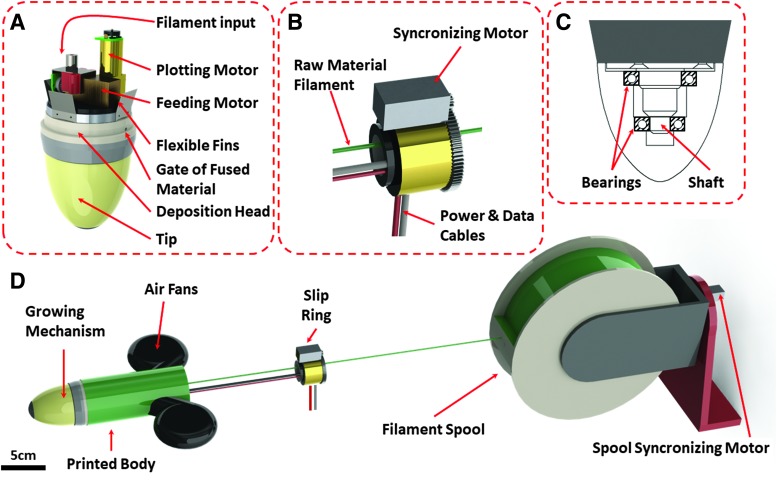
We have described our self-growing robotic root in previous works.¹³ In brief, the robot is equipped with a miniaturized and customized 3D printer inside its tip, which is used to actuate the forward movement by a material layer-by-layer deposition. The robot thus creates its own body in a tubular shape (Fig. 1A).

FIG. 1.

(A) Schematic view of the growing robot with feeding mechanism to automatically prevent the twisting of PLA filament with wires for power and communication. (B) Tip section view with two bearings for decoupling the tip from the rotation of the deposition mechanism. (C) Detailed view of the growing mechanism. (D) Close view of the hollow slip ring to avoid cable twisting. PLA, polylactic acid. Color images are available online.

We have subsequently improved the root-like robot and increased its degree of autonomy. In the previous version of the robot, the continuous rotation of the plotting unit twisted the filament of raw material with the power and data cables, which, after some cycles of deposition, interrupted the feeding, deposition, and communication actions. The new version of the robot now uses a hollow slip ring (MT2586 by Moflon Technology Co.), which decouples the rotation of the plotting disk from the power source and PC connection and, at the same time, enables the raw material filament to easily pass through the slip ring hole (Fig. 1B). We have also introduced another couple of spool gears at the container zone to counteract the accumulated torsion in the raw material filament by synchronizing the rotation of the spool with the plotting unit speed.

The tip is now connected to the deposition head by means of two ball bearings and a solid shaft (Fig. 1C). This design decouples the tip from the rotation of the deposition head. The rotational freedom of the tip prevents the tip from rolling when it comes across an obstacle, which would otherwise affect the accuracy of our study on obstacle avoidance by additive manufacturing.

The flexible fins in Figure 1A keep the 3D printer fixed to the built body and permit it to slide inside the structure without rotational slippage. To set the coordination of the plotting system with the printed body, we adopted a magnetic encoder in the deposition head with magnets placed in the internal side of the internal fins, which sets the zero point of the plotting at each cycle.

Finally, we have improved the cooling system, by adopting two fans that inject air up to the internal part of the robot through 3D printed channels, oriented at 50° in the direction of the tip, and installed at the sides of the robot (Fig. 1D). The cooling system prevents the electronics from overheating and becoming damaged. The overall assembly is shown in Figure 1D.

Experimental protocol

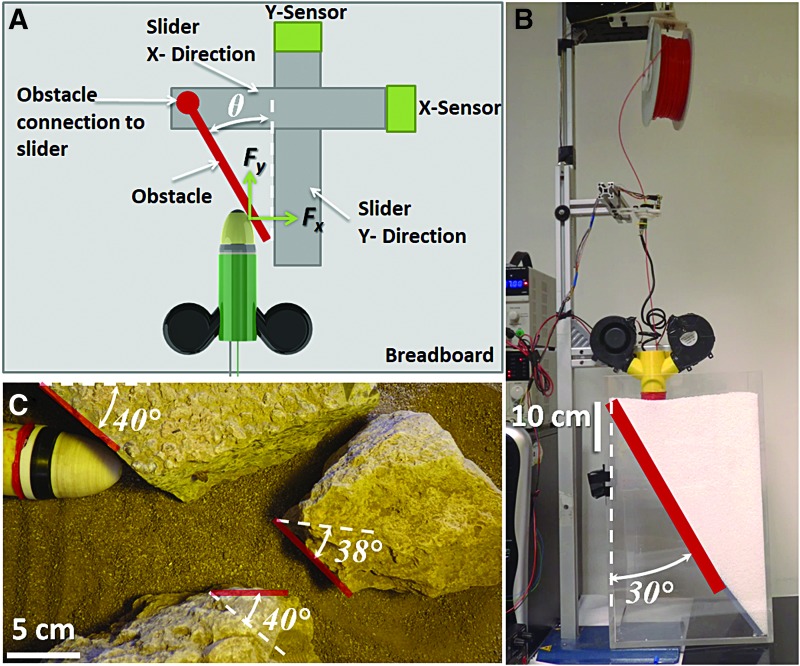
Our newly designed robotic root was placed above an optic breadboard (MB4545/M from Thorlabs) where we installed an ad hoc setup with an orientable obstacle connected to a multiaxis sensor system (Fig. 2A). The system consists of two monoaxial load cells (0–5 kg, CZL635; Phidgets, Inc.), each connected to a low friction slider (XR25C/M; Thorlabs) interconnected with the obstacle, to guarantee the isolation of x- and y-axis force direction (F_x and F_y). The angle of the obstacle can be mechanically regulated from 0° to 90°. The load cells are connected by two custom amplifiers (INA122P from Texas Instruments) to a data acquisition board (NI USB-6218; National Instruments) and acquired using NI Signal Express 2015 with a sampling rate of 100 Hz. The obstacle was in PMMA with a surface roughness of 0.25 μm Rz. We chose an obstacle with a very low friction to decouple the study of growing material adaptation from the study of tip–obstacle interaction. In fact, the tip–obstacle interaction is more related to the shape, material, and roughness of both the tip and obstacle and thus not strictly related to the deformability of the material of the body structure.

FIG. 2.

(A) Schematic view of the load cells and sliders connection with the obstacle. (B) Setup to test the robotic root in an artificial soil (polyoxymethylene granules, with a diameter of 4 mm) with an obstacle at 30°. The container had an inside dimension of 28 × 28 × 42 cm W × L × H, up to the soil surface, and the obstacle was placed diagonally. (C) Real unstructured environment reconstruction with rocks at different angles and sandy terrain. In (C), the barrier angles have been evaluated considering tip direction at the instant of incidence (white dashed lines). (A) Used to characterize body structural material behavior when facing an obstacle, purposely using a smooth surface. (B, C) Additional tests to verify the feasibility of our system to move in more articulated environments. Color images are available online.

The robot was programmed to only grow straight at a 20°/s constant plotting velocity and an ∼8 mm/s constant feeding velocity. The filament is ∼1.7 mm thick in input to the extruder and the heating temperature is 250°C. These settings result in a growth speed of 3–4 mm/min in air. This version of the growing robot does not include any sensors nor any specific control for obstacle detection and bending of the system.

We defined the setting parameters on the basis of our previous experiments.^13,41 We only changed the heating temperature, increasing it to 250°C to allow a better adhesion among subsequent layers, thus improving the strength of the structure and the polymer flow.

The growth evolution was recorded with a camera fixed to the breadboard and placed on top of the obstacle. The resulting video was used for postprocessing to extract tip orientation and robot path by thresholding using a MATLAB script.

The whole assembly for characterizing the passive adaptation of our root-like robot is presented in Figure 2A.

We performed and extracted data from four different trials with an inclination θ of the obstacle at 20°, 30°, 40°, and 50°, with five repetitions each. From the experiments, we extracted the force (F) exercised by the system on the obstacle as the Euclidean norm of the forces applied on the sensors (F_x and F_y). After the quantitative analysis and characterization, the system was also qualitatively evaluated in an artificial granular soil (made from polyoxymethylene granules, with a diameter of 4 mm), placing an obstacle at ∼30° (Fig. 2B), and letting the robotic root grow inside the soil until reaching and interacting with the obstacle. This underground environment is more difficult to navigate with respect to the air since the robot needs to exercise on average 47.2 ± 4.8 N at 20 cm of depth when penetrating in such soil. We also tested more complex surfaces and paths by simulating an unstructured environment in air, using sandstone rocks and sand to qualitatively validate the robot's ability to perform passive adaptation also with non-flat and highly irregular surfaces (Fig. 2C).

Results and Discussions

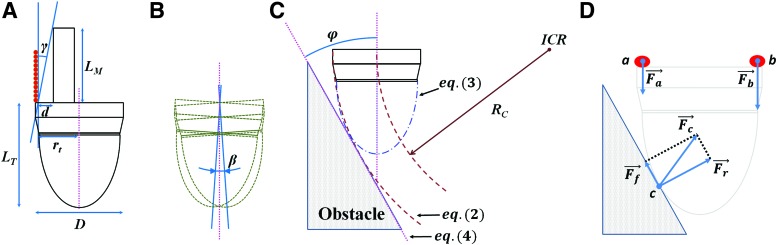
The main result was that the robot successfully adapted its path to the presence of obstacles at different angles (Fig. 3). The robot adjusted its direction of growth to the maximum barrier angle of 50°. This limit is imposed to prevent the components of the 3D printer from colliding at the backside of the system with the inner side of the built structure. In fact, there is a maximal curvature that the robot can actuate that has a minimum bending radius of 98.2 mm. The limit curvature radius can be found by analyzing the geometrical parameters of the system (Fig. 4A): length of the taller component assembled in the growing mechanism L_M, distance of the tallest component from the internal side of the built structure d, and distance from the center of the tip to the internal side of the structure r_t. These parameters provide the minimum radius from the relation:

FIG. 3.

The growing robot (whose tip diameter is 48 mm at its largest) after four trials of obstacle avoidance with 20°, 30°, 40°, and 50° of inclination θ with a flat barrier. Color images are available online.

FIG. 4.

(A) Main parameters of tip and growing mechanism: tip diameter D = 48 mm; tip length LT = 62 mm (h = 22 mm and e = 40 mm); length of the taller component assembled in the growing mechanism LM = 48 mm; distance of the taller component from the internal side of the built structure d = 10 mm; and distance of the tip center from the internal side of the built structure rt = 22 mm. (B) Tip oscillation induced during the circular deposition of material. Amplitude of this oscillation depends from material thickness; in our case, with a filament of 1.7 mm diameter, the amplitude β is ∼2°. (C) Drawing of the tip facing the obstacle with maximum angle φ, characterized by a curvature of the growing robot with minimum radius RC = 98.2 mm (ICR is the center of rotation). (D) Close view of the tip–obstacle interaction with the forces involved. When considering a simple 2D model, the extruder can be localized in either of the two points: a, where a force F_a should be exercised to extrude the material, or b, where the extrusion force is F_b. The tip enters in contact with the obstacle at a certain point c, where the friction force F_f and the reaction force F_r are localized and contribute in the resulting force Fc. 2D, two-dimensional. Color images are available online.

$$R_C=\frac{d^2+{L_M}^2}{2d}-r_t.$$ (1)

The limit barrier angle is the result of a combination of three main mechanical and geometrical constraints. First, due to the mechanical design of the deposition head, the whole assembly of internal components, affecting the minimum curvature radius, also creates an angle $\gamma ={tan}^{-1}\left(d∕L_M\right)$ with the straight direction (Fig. 4A), which in our design corresponds to 11.8°.

Second, since the deposition head moves circularly while extruding the material, the tip oscillates (Supplementary Video S1), which create a virtual cone with an angular aperture of $\beta$ (Fig. 4B). This oscillation is due to the thickness of the material and the root diameter, which in our system is ∼2°, when growing straight. Thanks to this embodied oscillatory circular movement (also known in plants as circumnutation),^42,43 the tip can potentially note in advance the presence of the obstacle and adjust its path, by touching the obstacle before the deposition zone comes in contact with it. The length of the tip (L_T), together with the amplitude of this oscillation ($\beta$), thus help adapt the shape of the body to the obstacle.

Third, the tip length (L_T) and shape can be used to find the common tangent between the tip and the circle of maximal curvature achievable by the system (with minimum curvature radius). This tangent also corresponds to the line lying on the obstacle surface (Fig. 4C).

Finding the tangent line entails the following three equations:

$${\left(x-\left(R_C+D\text{/}2\right)\right)}^2+y^2={\left(R_C+D/2\right)}^2,$$ (2)

$$\frac{{\left(x-D\text{/}2\right)}^2}{r_t^2}+\frac{{\left(y-h\right)}^2}{e^2}=1,$$ (3)

$$y=mx+q.$$ (4)

Equation (2) corresponds to the equation of the circle, where ICR is the center of rotation and the radius is $R_C+D/2$ (Fig. 4C). Equation (3) describes the tip, which is approximated with an ellipse, and Equation (4) describes a generic line. The tangent line to Equations (2) and (3) is found by imposing the tangency condition on both curves with the line lying on the obstacle. With the parameters of our system (Fig. 4), Equation (4) has $m=-1.42$ and $q=-38.7$, and the angle $\phi$ (Fig. 4C) is in our case 35.1°. The three contributions ($\gamma$, $\beta$, and $\phi$) impose a maximum obstacle angle $\overline{\theta }$ negotiable by our system equal to $\gamma +\beta ∕2+\phi$ = 47.9°.

This geometrical evaluation was partially confirmed by the experiments. Our robot was able to overcome the obstacle with a 100% success rate up to 40° angle, and the obstacle at 50° with 60% success rate (three times over five trials). This slightly overperformed achievement ($\overline{\theta }<$ 50°) was probably induced not only by a small misalignment of the tip but also by the fact that the robot changes the ICR of the curvature at each cycle when it adapts to the obstacle, producing a heterogeneous curvilinear structure, which avoids contact between internal components and the body.

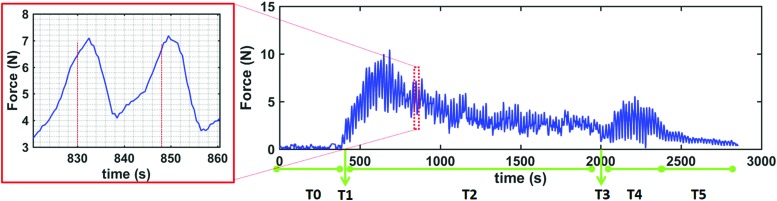
With the proposed setup (Fig. 2A), we monitored the forces exerted by the robotic root when in contact with the obstacle. Figure 5 shows an example of the contact forces acquired when the robotic root was facing an obstacle at θ = 50°. The graph highlights the various phases of contact. The robotic root initially approaches the obstacle with its tip (T1), and this first contact is identified with a jump in the forces which start to increase. Then, after a maximum peak (∼10 N), the tip starts to align to the obstacle and the force tends to decrease till T3, which is followed by a second rapid increase (T4) determined by the contact of the deposition module with the obstacle. The photos of the experiments in the final configuration (Fig. 3) show the adjustment of the root morphology until the robotic tip is aligned with the obstacle. Forces at this last stage (T5) tend to stabilize around a higher level, with respect to the initial phase (in no-contact condition [T0]), since the deposition head remains in contact with the obstacle.

FIG. 5.

Example of the forces acquired with θ = 50° from the multiaxis system. Each interval of time Ti identifies no-contact (T0) or contact of specific part of the robotic head: (T1) first contact of the tip with the obstacle, (T2) sliding of the obstacle along the surface of the whole tip; (T3) point of passage between tip and deposition head; (T4) contact of the obstacle with the deposition head; (T5) the robot has reached an almost parallel position of the head with respect to the obstacle. The zoom on the left shows a typical oscillation of the forces with a period of 18 s, corresponding to one single cycle of deposition. Color images are available online.

Force analysis during tip–obstacle interaction involves many system parameters: the tip length, shape, and material affect the friction forces; the extrusion temperature affects the body material flow and behavior; the plotting speed affects the cooling time before compression; the feeding speed, which combined with the plotting speed, influences the amount of material extruded in a unit of time; the environmental temperature also affects the material cooling time; and finally, the internal tip temperature, which changes during the growing process, and the mature body length.

A complete evaluation of the forces involved in the process of growth, taking into account all these elements, would include a study of the thermal properties and a thermofluid dynamic analysis. But such an analysis goes beyond the aim of this article and will be investigated in the future work. However, for the purposes of the current work, the obstacle negotiation can be approached as a two-dimensional problem, where two main conditions can occur. First, the extruder is close to the obstacle (point a in Fig. 4D), in this case, the opposite side of the body is assumed to work as a revolute joint. Second, the extruder is at its farthest point from the obstacle (point b in Fig. 4D), in this case, the revolute joint is located at the side of the body close to the obstacle.

To enable the growth, the extruded material has to overcome the torque associated with the resulting force (${\vec{F}}_c$), obtained by the contribution of the reaction force ($\overrightarrow{F_r}$) and the friction force (${\vec{F}}_f$). When the extruder is in point a, the major contribution derives from ${\vec{F}}_f$, which we decided to limit in our setup and thus ${\vec{F}}_a$ tends to be small. However, when the extruder is in point b, the tip is physically constrained by the obstacle and a completely rigid system will be locked. However, due to some flexibility in the overall setup (induced by joints in the tip and in the multiaxis sensor system), the robot still has some maneuverability. For plotting to be successful, the material thus has to generate a force (${\vec{F}}_b$) that can overcome a torque generated by the reaction force ($\overrightarrow{F_r}$). The greater the reaction torque, the smaller will the resulting thickness of the plotted material.

This oscillatory behavior between a minimum and a maximum force (F) was confirmed in our experiments (Fig. 5) where oscillation lasted one growth time step (18 s) (inset Fig. 5). The continuous oscillation of the head is due to the circular deposition of the filament actuated by the plotting mechanism. This oscillation, whose amplitude relates to the inclination of the tip with the obstacle, can be used in soil. However, it could be mitigated under the pressure of the soil itself when attempting to identify the presence and the position of an obstacle with respect to the point of deposition in the robot. The difference between the maximum and minimum F is expected to be small in homogeneous soil, but to increase in the presence of heterogeneity.

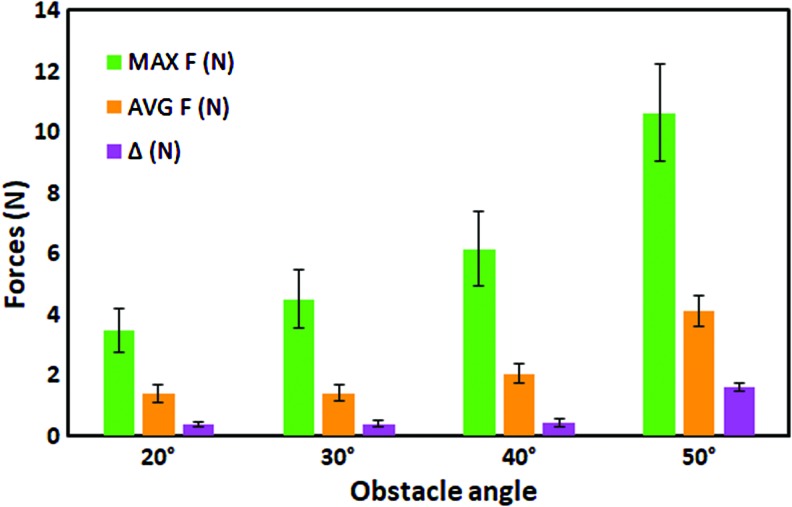
The maximum resulting force (F), measured on the obstacle by the two load cells of the setup, increases with the angle (Fig. 6, green bars) up to 10.6 ± 1.6 N for 50°. Another interesting result is the average force measured during the interaction between the tip and the obstacle, which also slightly increases with the angle and varies from 1.38 to 4.12 N for angles from 20° to 50° (Fig. 6, orange bars).

FIG. 6.

Results of force measurements from tip–obstacle interaction at different angles: in green, the maximum force measured; in orange, the average force measured during the interaction; in violet, the average oscillation of the force measured. Color images are available online.

Finally, we also plotted (Fig. 6, violet bars) the amplitude of the oscillations ($\Delta$) measured during the tip–obstacle interaction. This value is calculated as:

$$\Delta =\frac{\sum \left|F\left(T\right)-F\left(t\right)\right|}{N},$$ (5)

where t is the time of the minimum peak, T is the time of the maximum peak, and N is the number of oscillations. In this case too, $\Delta$ tends to slightly increase with the angle; however, the effect of the barrier angle is more relevant with a limit value of θ = 50° for all the three values (max, avg, and $\Delta$).

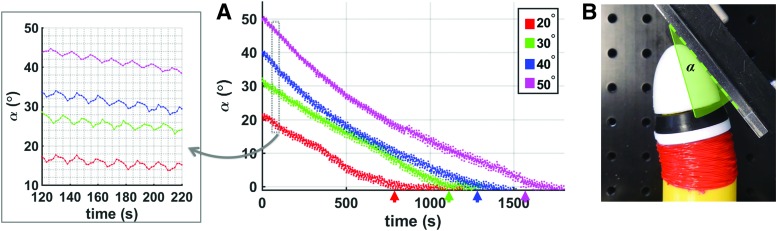
Figure 7A shows the orientation of the root tip with respect to the obstacle (represented by the $\alpha$ angle, Fig. 7B). For $t=0$, $\alpha$ is maximal and the tip has started making contact with the obstacle; when $\alpha \cong 0$, the tip is configured parallel with the obstacle. As expected, the alignment time varies with the inclination of the obstacle (colored arrows below the x-axis in Fig. 7A show when the initial alignment began).

FIG. 7.

(A) α Angle along time, from the first time of contact, with the obstacle at different inclination. Colored arrows indicate the instant of initial alignment (tip and obstacle are parallel, α = 0). The inset at the left bottom side shows a close view of the oscillatory behavior obtained by the rotary motion of the growing mechanism. (B) The reference α angle: the inclination of the tip with respect to the obstacle. Color images are available online.

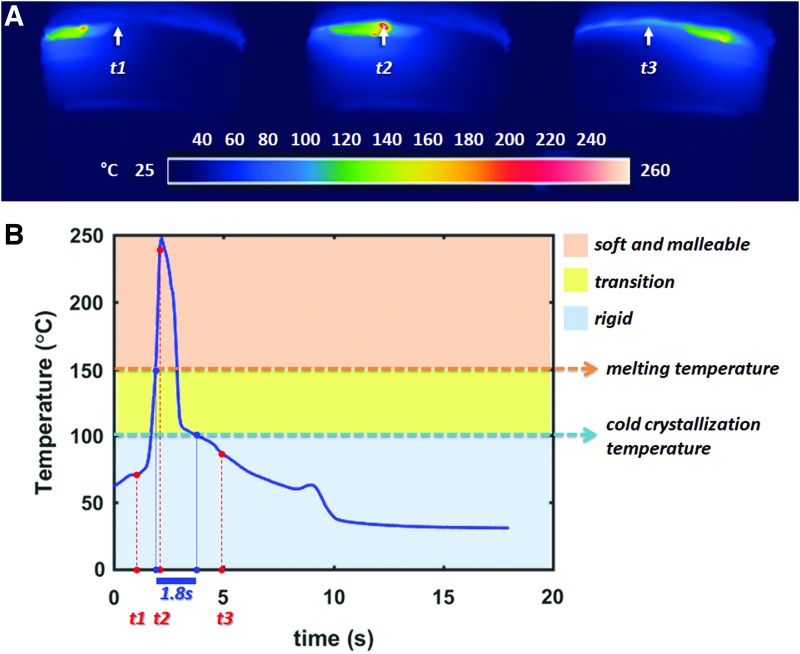
As we had hypothesized, the flexibility of the material at the deposition zone and the flexibility of the plotted zone before solidification are keys for the robot's passive adaptation. Figure 8A highlights that PLA at the extruder reaches a temperature of 250°C, far above its melting temperature, which is typically 150°C, and this leads to its transition into the soft phase.⁴⁰ Figure 8B shows the evolution of the temperature for a single fixed point in the structure in one cycle of deposition. The temperature decreases below 100°, which typically defines the cold crystallization temperature,⁴⁰ in a few seconds (1.8 s), which represents the time frame for molding the material. This short cooling time (less than one cycle—18 s) also confirmed the assumption of using the opposite side of the extruder as a revolute joint, since it is in its solid state.

FIG. 8.

(A) Sequence of material deposition obtained with IR thermal camera (A325sc; FLIR Systems). (B) Temperature profile of a fixed point along the structure, from time of extrusion, for a single cycle of deposition (18 s). The point is highlighted with white arrows in (A) and corresponding time (t1, t2, and t3) in (B). (B) Also shows critical temperatures and material phases of PLA34. Color images are available online.

By exploiting the soft state of PLA, bending can be achieved not only with control over the deposition parameters but also due to how the material can change form in reaction to external loads before complete solidification. Also, based on the heat transfer and dissipation conditions of the surrounding area, and on the deposition speed, the melted polymer at the deposition zone can solidify in different ranges of time. There is thus a transition zone between the completely melted polymer and the solid state of the polymer that starts at the exit gate of the extruder and holds until it has reached the old and solid part of the structure (Fig. 8).

The flexibility of the transition zone (extended for ∼36° of the circular deposition in the air) enables the growing robot to passively adapt to environmental constraints. For example, in the case of soil with high impedance, the flexibility of the transition zone results in a structure with a very thick wall that gives the system greater structural strength, which is needed to resist the high soil pressure (as demonstrated by the weight lifting test).⁴¹ However, in the presence of an obstacle, for example rocks, a lateral load causes an asymmetric deformation of the material: one side of the robot is compressed (in the transition region opposite the obstacle) under the reaction force exerted by the interface with the barrier, squeezing the material. On the opposite side, the polymer is easily released. This results in a curved tubular structure that bends toward the thin side.

Due to this principle, different morphologies (Fig. 3) are obtained, even though the control was the same for all experiments (i.e., straight growth) and the growth speed remained constant all the time (3–4 mm/min). The interaction with the environment defines the final morphology of the robot's body and its behavior in relation to the thickness and symmetry of the layers.

Finally, we tested how well the robotic roots penetrate artificial soil and avoid a 30° obstacle, obtaining a successful 16 cm penetration into the soil with the desired bending (Supplementary Video S1).

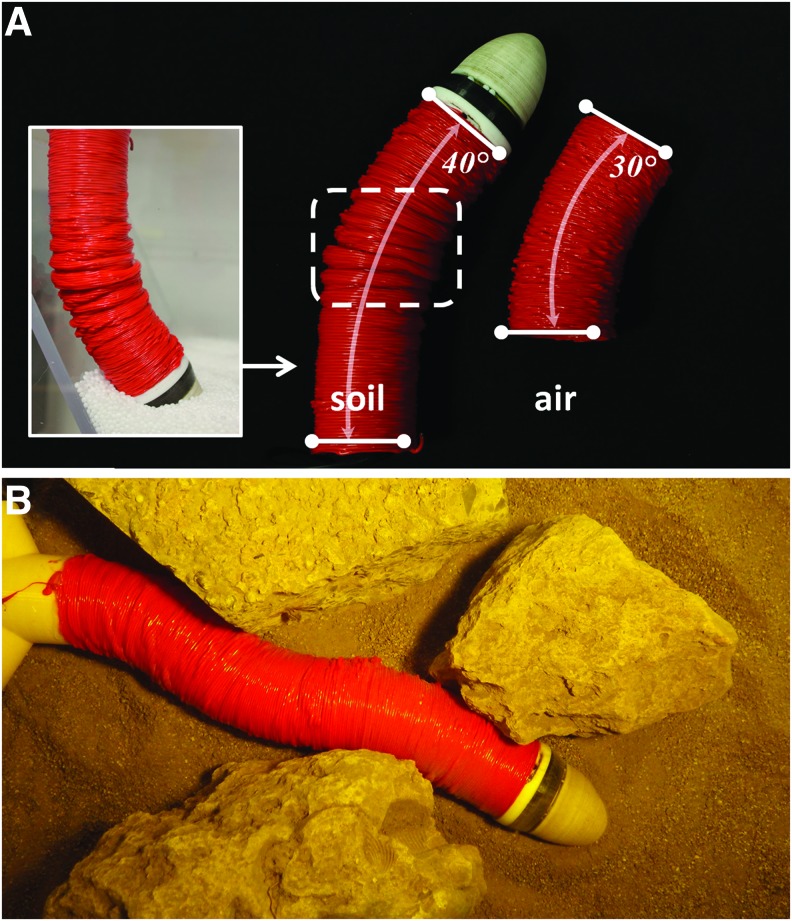
As shown in Figure 9A, the structures obtained from the robot growing in air and soil with the same barrier angle have a completely different shape and curvature. In fact, the presence or absence of soil around the robot affects heat dissipation; thus, in the soil, the deposited PLA remains malleable for longer. This slower heat dissipation, combined with the pressure imposed by soil and barrier, produces an irregular enlargement of the structure when the tip is still inclined with respect to the obstacle (Fig. 9A in the dashed rectangle). When the tip is aligned with the obstacle, the structure becomes more regular again and geometrically similar to the one obtained in air.

FIG. 9.

(A) A comparison between the structure obtained by the robotic root growing into artificial soil (polyoxymethylene granules, with a diameter of 4 mm) with an obstacle at 30° (left and inset), and the structure obtained growing in air and facing the obstacle with θ = 30° with the setup in Figure 2A. The result is shown after soil removal. Dashed white rectangle highlight the region of deformation produced by the impact with the obstacle in soil. (B) The final S shape resulting from navigation in unstructured environment with rough barriers. Color images are available online.

Generally, the structure produced in soil has a thicker body wall (external root diameter on average of 56 mm) with a stronger layer adhesion, which results in a stronger body with respect to the one grown in the air (with an external root diameter on average of 47 mm). This wall thickening recalls the radial expansion obtained in plant roots when growing in an impeding medium.^37,38,44 In addition, we obtained a final curvature in the structure of 40° (instead of 30°), probably induced by an uneven top layer distribution of the granules. This behavior suggests that when the robotic root moves in soil, it tends to follow the most convenient direction in terms of resistive force; in fact, the root was growing toward the direction of the shallower soil, thus having a lower lithostatic pressure.

We also tested our system in a real unstructured environment letting it grow for 27 cm between rocks over an uneven sandy terrain (Fig. 9B and Supplementary Video S1). The robot was able to move and adapt its body to the presence of small hills and rough obstacles, and in the final stage had an irregular S shape.

These results demonstrate that the robot can passively adapt its path and morphology to obstacles, even with different degrees of roughness (from flat to irregular surfaces) and impeded environments.

Conclusions

We have shown the ability of a plant-inspired growing robot to passively adapt its body morphology, and consequently to dynamically adjust its path, when higher resistance (a barrier) is found in the medium where it moves. The adaptation is obtained thanks to the change in the properties of the PLA material, going from solid to its soft phase, when it is heated at 250°C and extruded with a velocity of ∼8 mm/s. In this phase, the material is ductile and can take any shape. Thus, when facing an obstacle, the tip of the robot is subjected to a lateral force that squeezes the material on the opposite side of the barrier because of the compression exerted on that side, obtaining a thinner height, while printing a thicker height on the side of the obstacle (due to the resulting smaller compression force).

The intelligence of the system comes from its mechanics, with no need for a specific control for obstacle avoidance. This behavior passively computed by the body in response to environmental interaction, which is also called “intelligence by mechanics” or “morphological computation,”²⁵ is a desired feature in robots moving in unstructured environments as it enables a safer interaction between the robot and the environment while lightening the control.^45,46

Our robot demonstrates several plant-like behaviors^38,47,48 in terms of adaptation of the robotic root morphology to environmental physical constraints. First, the robot has a passive structural failure, or buckling, caused by the mechanical perturbation obtained in interaction with obstacles. Second, this structural deformation causes a passive repulsive response to the obstacle. Third, the highest impedance faced by the robot when growing in soil causes a radial expansion in the robot's body.

Likewise in plants, the active thigmotropism can be anticipated by an autonomous mechanical adaptation of the body, which is obtained at least until a minimum threshold level of stress,⁴⁷ after which complex internal processes have a stronger influence on controlling the bending.^30,31,47

From a robotic perspective, our system, as in the natural model, exploits material properties, body dynamics, and interaction with the environment to perform a complex task, such as obstacle avoidance, without a cognitive process. The experiments on the force applied by the robot and measured using the multiaxis setup demonstrated that it is also possible to identify the presence of an obstacle when there is a sudden increase in force, and its position, by localizing the direction of the point of maximum force during one cycle of growth.

By observing the behavior of plant roots in a natural environment, we can improve the movement of our robot in soil by merging passive and active responses to touch in our robotic root, thus further decreasing the interaction forces. In fact, by integrating a multiaxis force sensor in the tip, it would be possible to detect when resistance forces rise above a certain threshold limit and consequently prevent a possible break of the system by changing the strategy for penetration.

Additional analyses in real and different types of soil are needed to better define the behavior of forces and the ability of our system to adapt. The interaction between different degrees of roughness in the obstacle and the tip material would produce different reaction forces and consequently a different behavior that need to be more extensively and quantitatively analyzed. However, this study helped us to characterize the behavior of the robot body–structural material in interaction with the external environment and above all highlighted how the system can passively shape its body, with a consequent reduced complexity in the adopted control strategy.

Further steps will include a design and analysis of the shape and material of the tip to improve the interaction between the tip and the obstacle, thus facilitating navigation in a cluttered environment.

Authors' Contributions

A.S. designed and fabricated the robot, designed the experiments, and fabricated the setup. E.D.D. and A.M. designed and performed the experiments and processed the results. A.S., E.D.D., and A.M. analyzed and discussed the results, and wrote the article. B.M. conceived and oversaw the research, discussed the results, and revised the article.

Author Disclosure Statement

There are no competing financial interests.

Funding Information

This study was partially funded by the RoboCom++ project (FLAG-ERA Joint Transnational Call 2016), by SMASH—Smart Machines for Agricultural Solutions Hightech (Tuscany-Italy POR FESR 2014-2020), and by the European Union's Horizon 2020 Research and Innovation Programme under Grant Agreement No. 824074 (GrowBot project).

Supplementary Material

Supplementary Video S1