Figure 1. Common PK-PD models.
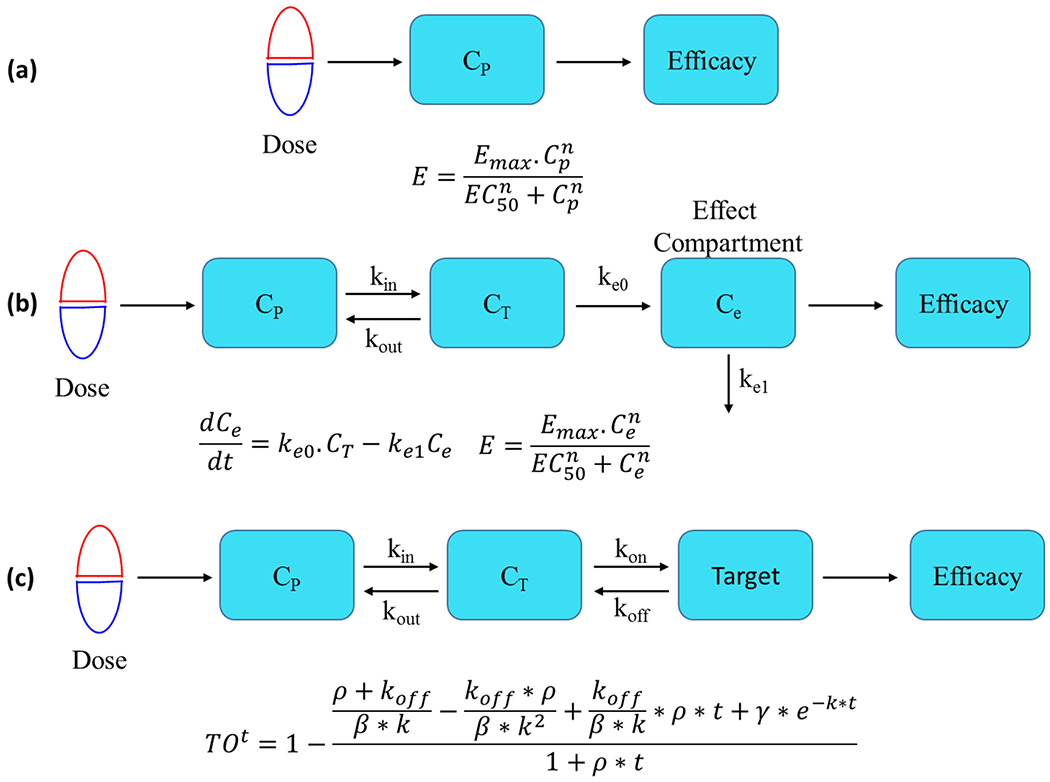
(a) A simple Hill-based direct link-direct response model. CP is the concentration of drug in plasma, and drug concentration and response are connected by a sigmoidal Emax model where E is the observed efficacy, Emax is the maximum efficacy and n is the Hill coefficient that describes the steepness of the response. (b) A Hill-based model with an effect compartment. Cp, CT and Ce, are the drug concentrations in plasma, target tissue and effect compartment, respectively. kin and kout are the first order rate constants for the distribution of drug from the plasma to the tissue and drug release from the tissue to the plasma, respectively, and keo and ke1 are first order rate constants for drug entering and leaving the effect compartment which is included to compensate for the temporal dissociation between concentration and response, and thus to account for hysteresis. In the absence of hysteresis, the effect compartment is excluded from the model. In the sigmoidal Emax model, Ce is the drug concentration in the effect compartment. (c) A target occupancy (TO)-based model that includes a term for the rate of target turnover (ρ). The model has two dynamic sections including a PK term that defines the time-dependent change in drug concentration in plasma/tissue, and a binding kinetics term that controls the time-dependent change in target occupancy (TO) as a function of drug concentration at the target site. Drug-target complex formation is assumed to occur in a single step where kon is the second order rate constant for binding and koff is the first order rate constant for dissociation. TOt is the fractional target occupancy as a function of time (t), where ρ is the rate of target turnover, where Km is the Michaelis-Menten constant and [S] is the substrate concentration, where [I] is the inhibitor concentration and , is the apparent equilibrium inhibition dissociation constant for the one-step binding mechanism, and .
