Figure 3.
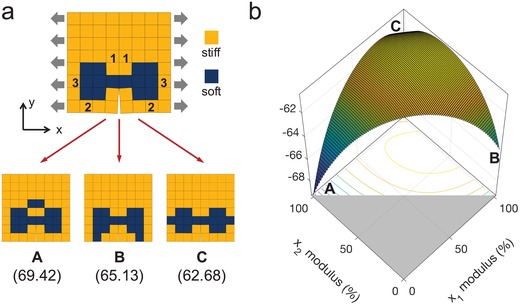
A composite design problem with a volume fraction constraint under Mode I fracture. a) An 8 by 8 composite system made up of stiff and soft base materials. Stiff and soft materials are shown in yellow and blue, respectively. The composite on the top is the optimal design with a volume fraction of 21.875% for high toughness. The composites on the bottom are three possible designs with a volume fraction of 25%, denoted by Composite‐A, Composite‐B, and Composite‐C. The numbers below indicate the corresponding toughness values; b) The optimization surface and contour plot of the composite design problem with a volume fraction constraint of 25%. The horizontal axes represent the modulus ratios of Element‐1 and Element‐2 and are denoted by x 1 and x 2, respectively. The modulus ratio of Element‐3, denoted by x 3, is a dependent variable as the summation of x 1, x 2, and x 3 is 200% due to the volume fraction constraint. The vertical axis represents the objective value, which is set to be the negative of the toughness. Composite‐A, Composite‐B, and Composite‐C represent the three boundary points in the optimization surface.
