Network explanations and explanatory directionality

Abstract

Network explanations raise foundational questions about the nature of scientific explanation. The challenge discussed in this article comes from the fact that network explanations are often thought to be non-causal, i.e. they do not describe the dynamical or mechanistic interactions responsible for some behaviour, instead they appeal to topological properties of network models describing the system. These non-causal features are often thought to be valuable precisely because they do not invoke mechanistic or dynamical interactions and provide insights that are not available through causal explanations. Here, I address a central difficulty facing attempts to move away from causal models of explanation; namely, how to recover the directionality of explanation. Within causal models, the directionality of explanation is identified with the direction of causation. This solution is no longer available once we move to non-causal accounts of explanation. I will suggest a solution to this problem that emphasizes the role of conditions of application. In doing so, I will challenge the idea that sui generis mathematical dependencies are the key to understand non-causal explanations. The upshot is a conceptual account of explanation that accommodates the possibility of non-causal network explanations. It also provides guidance for how to evaluate such explanations.

This article is part of the theme issue ‘Unifying the essential concepts of biological networks: biological insights and philosophical foundations’.

1. Network explanations and evaluations of model aptness for explanation

We are often interested not only in prediction but in understanding what is responsible for the behaviour, pattern or phenomenon that we are interested in; we are interested in explanations. Scientific explanations based on network models bring to the surface foundational questions about the nature of scientific explanation.

On the one hand, many applications of network models appear explanatory while not providing causal mechanistic information. For example, Huneman [1] and Kostić [2] both argue that network models are sometimes genuinely explanatory but not by providing information about causal processes. Instead, they argue, network models sometimes derive their explanatory power from topological properties of the network model. Kostić [2, pp. 80–81] gives an example of explanation using Watts & Strogatz’s [3] small-world graph model and the spread of infectious disease.

In topological explanation, the explanatory relation (the relation between the explanans and explanandum) stands between a physical fact or a property and a topological property. In the Watts & Strogatz [3] example, we have seen that the explanation of the physical fact is a function of the system topology, i.e. in this example, small-world topology shortens the path lengths between the whole neighbourhoods, and neighbourhoods of neighbourhoods and in that way the infectious disease can spread much more rapidly.

These types of examples push towards regarding network models as explanatory of physical facts in ways that do not fit with taking explanations to provide information about causal dynamical or mechanistic interactions.

On the other hand, a common way to distinguish mere predictions from explanations is to distinguish between mere correlations and causation. In particular, many philosophical accounts of scientific explanation of physical facts rely on the directionality of the causal relation (from cause to effect but not vice versa) to account for the directionality of explanation and to distinguish mere prediction from explanation.¹ Once we allow non-causal network explanations of physical facts we face the difficulty of distinguishing explanatory from non-explanatory network model applications in some way that allows us to recover the distinction between mere prediction and explanation. Craver [6, p. 707] stresses this challenge (taking it to push against recognizing network explanations as a type of non-causal explanation).²

The problem of directionality and the puzzle of correlational networks signal that, at least in many cases, the explanatory power of network models derives from their ability to represent how phenomena are situated, etiologically and constitutively, in the causal and constitutive structures of our complex world.

This article presents an alternative way of addressing the problem of directionality. Instead of focusing on directed notions, such as causation, I will suggest a solution focused on taking into account background knowledge about the network model's conditions of application. That is, I will focus on the conditions that have to hold in order for the model to aptly be applied to the system of interest. This removes one source of worry about non-causal network explanations. They do not require a new directed metaphysical notion akin to causation where it can be unclear what this relation is and how we can evaluate whether it holds.

2. Assumptions about explanation

I will work with the assumption that explanation is distinguished from prediction by providing information about what the explanatory target (the explanandum) depends on. That is, explanations offer information about what would have happened in non-actual circumstances as well as information about what can be predicted to hold given the actual circumstances. This focus on counterfactual information is in common with several accounts of causal explanation (notably, [4]). On its own, this focus on dependence does not yet provide us with a solution to the problem of directionality. In Jansson [8], I argued that we can provide a solution to the problem of directionality when it comes to law-based explanations by focusing on the law’s conditions of application. This solution does not, however, cover the types of non-causal explanations that we seem to find in network explanations where topological properties are doing the explanatory work. To start to cover such network explanations, I need to say a little more about the schematic structure of explanatory models of physical facts that I am working with. I take the process of giving a model explanation to have as a target a dependence external to the model (type 4) and to have three steps that are of interest when capturing the directionality of network explanations (dependence of types 1–3) (figure 1).³

Figure 1.

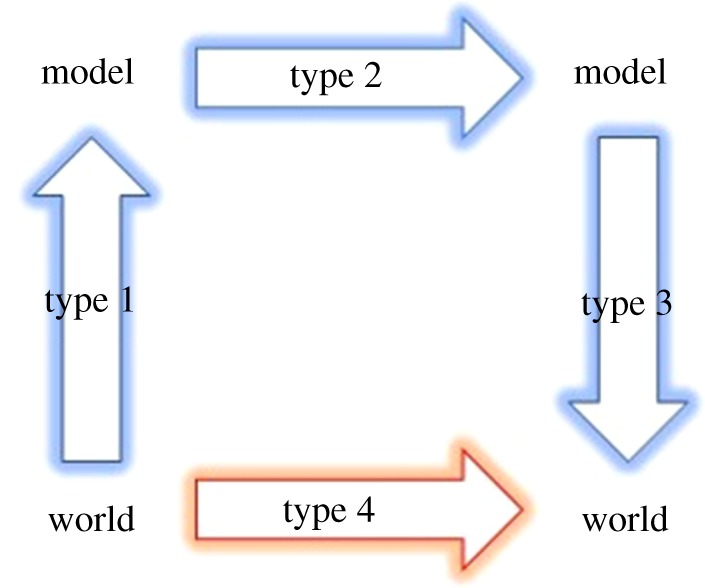
A simplified modelling schema showing four types of dependence. Types 1–3 are dependencies involved in the modelling process while type 4 is the dependence that is the target of the model. The arrows run from dependee to depender (the depender depends on the dependee). (Online version in colour.)

First, we can ask how features of the model selected vary with features of the explanatory target (type 1). Here, the model’s conditions of application are crucial. When we are selecting a model for some particular explanatory target, we typically confront questions about whether or not a particular model is apt. For example, in order to judge whether a particular type of pendulum can aptly be modelled for some purpose by using a simple pendulum model we need to answer questions such as: Is the pendulum forced? Is the amplitude of swing small? Is the mass of the pendulum rod negligible? Is the friction at the pivot low?, etc. Once we decide that a simple gravitational pendulum model is an apt model of the target, these considerations are typically no longer explicitly represented in the model itself. Second, we can ask how features explicitly represented in the model chosen depend on other features similarly explicitly represented (type 2) (figure 1). For example, in the simple pendulum model, the period is a function of the length of the pendulum rod and the acceleration due to gravity at the location of the pendulum. Third, we can ask how features of the target system can be expected to vary when features of the model do (type 3).

If we are willing to grant my starting assumption that explanation is a matter of providing information both about what can be predicted to hold given the actual circumstances and information about what would have held had circumstances been different, then there are multiple sources of information about such dependencies in the three steps outlined above. If we are interested in dependencies of type 4 but are approaching them via a modelling processes then all of types 1–3 are needed.

It is tempting to take only the dependencies explicitly represented in the explanatory model (type 2) to matter. However, this would be a mistake on the view outlined above. In this article, I will be particularly interested in how dependencies that capture what it takes for the model to be an appropriate model for the problem at hand (type 1) enter into explanations by the model. In order to take the dependencies internal to model (type 2) to have succeeded in capturing part of what the explanatory target depends upon, those dependencies have to be capable of being embedded in a fuller account of the dependencies of the explanatory target. When the explanatory target is sensitive to variations in the conditions that make the application of the model apt, then we might take the dependencies internal to the model (type 2) to be part of a broader account of what the explanatory target depends upon. This broader account of what the explanatory target depends upon includes considerations of what the model aptness depends upon (type 1). If, however, the explanatory target does not depend on the conditions that make the model apt, then we have no reason to view the dependencies within the model itself (type 2) as a partial story of the full dependencies of the explanatory target. There is now no reason to take the internal dependencies (type 2) to be part of a modelling schema that considers type 1–3 dependencies relative to the explanatory target.⁴

This is not to deny that when the conditions which make the model apt hold, we can have reason to take the model to be predictively accurate. However, being predictively accurate in the actual circumstances does not show that we have a model capable of being trusted to answer questions about what the explanatory target would have been like had circumstances been different. To do this, we require reliable dependence information throughout (from types 1 to 3).

For example, consider again the case of modelling a particular type of pendulum by using a simple pendulum model. Let us say that the explanatory target is the period of the pendulum. Here, the simple pendulum model can be explanatory. The model itself details the dependence of the period on, for example, the length of the pendulum rod. In addition, the explanatory target, the period of the pendulum, is sensitive to violations of the conditions that make the model apt. For example, in general, had the friction at the pivot not been negligible then the period of the pendulum would have been different, etc. The same does not hold for the intuitively predictive but non-explanatory application of the simple pendulum model to calculate the length of the pendulum rod. Within the simple pendulum model, the length can be expressed as a function of the period and the acceleration due to gravity. This is what allows the model to be predictively successful in calculating the length of the pendulum rod when the conditions for the model to be apt are fulfilled. However, the length of the pendulum rod is not sensitive to whether or not the conditions of aptness for the model are fulfilled. For example, we do not have reason to think that had the friction at the pivot not been negligible then the length of the pendulum rod would have been different.

3. Direction without a directed relation

The suggestion that I have outlined above is one that allows us to recover the directionality of explanation without postulating any particular directed relation that is responsible for the directedness of explanation of a certain type. An otherwise common response is to argue that the directedness of the causal relation (from cause to effect) is responsible for the direction of causal explanation. This approach leaves the directionality of non-causal explanations unaccounted for unless we can postulate a similar directed notion in the case of non-causal explanations. There are several suggestions that do this. For example, Pincock [9] ([1,2] also have versions of such proposals) postulates a type of sui generis directed relation of dependence from the more abstract to the less abstract in order to account for a type of non-causal explanation while Lange [10] makes use of a distinction between strengths of necessity.⁵ In the case of network explanations, Craver [6, p. 701] suggests that they sometimes require a directed non-causal notion of constitution.

Network properties are explained in terms of nodes and edges (and not vice versa) because the nodes and edges compose and are organized into networks. Paradigm distinctively mathematical explanations thus arguably rely for their explanatory force on ontic commitments that determine the explanatory priority of causes to effects and parts to wholes.

The suggestion that I am making in this article differs from all of these approaches in that it does not start from the postulation of some metaphysical asymmetric relation that is used to account for the direction of explanation. Rather, the directionality in explanatory applications of network models to physical facts is identified either from within the model or from an asymmetry in the sensitivity of the explanatory target to the conditions they have to obtain in order for the model to be aptly applied. There are several advantages to this approach. First, the problem of identifying the direction of explanation is transformed from a metaphysical problem where we face the challenge of how we can determine whether the appropriate relation holds, to an epistemic one. When there is a dispute over the direction of explanation (if any) for a particular case, we do not immediately need to settle metaphysical questions over which relation holds.⁶ Of course, this is not to say that it is always easy to determine the direction of explanation (if any), but the type of questions that we have to answer are theoretically and, sometimes, directly empirically tractable.

Second, it allows for a unified treatment of causal and non-causal explanations of physical facts. This is important when we are dealing with explanations from connected models that cross the causal/non-causal divide, and particularly so in cases where a multiscale model covers scales that are typically treated very differently. For example, Pedersen et al. [12] summarize such challenges in modelling an avian compass as a distinctively quantum process. The proposed model of avian navigation is radically multiscale because it involves both distinctively quantum notions such as entanglement and distinctively higher scale notions such as bird behaviour. Shrapnel [13, pp. 409–410] articulates the difficulty of recovering the directionality of explanation in these cases.

Many philosophers believe that scientific explanations display an asymmetry derived from underlying causal structure [5,14,15]. From this perspective, the explication of the phenomena listed above provides clear support for the existence of quantum causation. The philosophical literature, however, contains considerable skepticism concerning objective quantum causal structure [16–18]. Typically, those who eschew quantum causation derive their arguments from analysis of the correlations that appear in EPR type experiments, the problem being that while the measurement results in such experiments are clearly strongly correlated, they are thought not to be so in virtue of underlying causal structure.

The need to capture directionality in multiscale explanatory models has been part of the motivation to develop quantum causal models (QCMs).⁷ However, these models come with challenges, particularly when combined with other causal models in order to provide multiscale explanatory models.⁸

This article explores an option that avoids imposing uniformity by exporting causal frameworks for explanation to (intuitively) non-causal cases. In the next section, I will argue that the approach which focuses on conditions of apt model application is promising in addressing directionality in non-causal cases.

4. Königsberg’s bridges

In §§1 and 2, I argued the need for criteria for determining when a model appropriately captures the direction of explanation and highlighted some of the advantages of doing this in terms that are neither directly causal nor given by a metaphysical analogue to causation. I think that attention to the sensitivity of the explanatory target to violations of the conditions of application of the model are a promising source for recovering this directionality in non-causal terms.⁹ However, network explanations seem particularly problematic for the prospect of allowing us to recover the directionality of explanation without some sui generis notion of a directed relation between mathematical properties and physical phenomena.

Let me illustrate the problem and the suggested solution with the familiar case of Königsberg’s bridges and the graph-theoretic explanation of the impossibility of making a tour of the (historical) Königsberg by crossing each and every of its seven bridges exactly once and returning to the starting point. Below is Pincock’s description of the explanation of the impossibility of touring Königsberg in the way described above that appeals to the graphs in figure 2.

Figure 2.

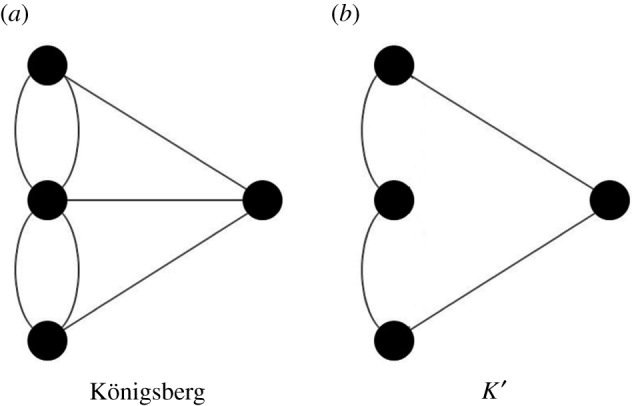
The two graphs relevant to Pincock’s explanation. (a) Königsberg, (b) K′.

[A]n explanation for this is that at least one vertex has an odd valence. Whenever such a physical system has at least one bank or island with an odd number of bridges from it, there will be no path that crosses every bridge exactly once and that returns to the starting point. If the situation were slightly different, as it is in K′, and the valence of the vertices were to be all even, then there would be a path of the desired kind. [22, p. 259]

In this case, it is possible to run inferences in both explanatory and (intuitively) non-explanatory directions. The appeal to the existence of a vertex with an odd valance seems explanatory of the impossibility to do the suggested round tour. However, the impossibility to do the suggested round tour also allows us to infer the existence of a vertex with an odd valance (given that the graph is connected). However, it does not seem to explain the existence of such a vertex. If we want to accommodate this difference in explanatory directionality in a non-causal way, we need to locate a difference that is not visible as a difference in implication when the model’s conditions of application are fulfilled.

Some aspects relevant to explanatory directionality can be recovered from within the model itself and so hold whether or not the model has a physical fact as the explanatory target. For example, while the graph determines the valence of the vertices, the valence of the vertices do not (in general) determine the graph. This contributes to the directionality mentioned in Jansson & Saatsi [11]; merely fixing that the bridge system in question cannot be toured in the suggested way does not fix the bridge system to any particular configuration but fixing the bridge system to a particular configuration does determine its round-tourability.

However, this is not enough for a full solution to the directionality of explanation in this case. The issue facing us now is that the non-tourability (in the suggested way) of the bridge system in question does fix the existence of at least one vertex with an odd valance and vice versa. If this was the full story then we would get the result that the non-tourability of Königsberg explains the existence of at least one vertex with an odd valence. This suggests that directionality from within the model is not the only source of explanatory directionality.

My suggestion is that this is where we need to consider the conditions of application of the model. Within a dependence account of explanation, we are interested in information about what the explanatory target depends on. When we are explaining physical facts, some information about how the target would have been different had other conditions been different can be expected to come from within the explanatory model itself. However, once we recognize that explanatory models typically have limited areas of application, part of what the explanatory target depends on is likely to be captured in the conditions of application. While we typically do not have a perfect understanding of the conditions of application, we can generally articulate such conditions (at least in outline). When we do so, we are, on this view, providing a better understanding of what the explanatory target depends upon and, thereby, providing more detailed explanations.

The model’s conditions of application provide an avenue for recovering directionality of explanation beyond what is explicitly covered in the explanatory model itself. We can have good reason to take a particular target to depend on the conditions of application of the model in question and to take the model to be an explanatory one. Alternatively, we can have good reason to take a particular target to fail to depend on the conditions of application and the model to fail to be an explanatory model even while maintaining that the model is (when the conditions of application do hold) inferentially reliable. To illustrate this, consider our case of making use of a graph-theoretic model to explain the non-tourability of Königsberg by the existence of at least one vertex with an odd valance. At first glance, it is easy to overlook the conditions that make the application of the model appropriate because they are so readily available. Nonetheless, the model in question is only appropriate under the assumption that the bridges are the only way to travel between the different parts of Königsberg, are such that they are possible to cross at will, etc. If such conditions hold and the graph-theoretic model is appropriate to use, then we can support the inference both from the existence of a vertex with an odd valance to the non-tourability of the bridge system and vice versa. However, only the round-tourability of the bridge system depends on the conditions of application. The tourability of the bridge system is, in general, sensitive to whether or not these conditions hold. Whether it is possible to make the described round tour depends on whether the bridges are the only permitted way of travelling between the different parts of Königsberg, whether they can be traversed, etc. However, the valance of the vertices is not sensitive to these conditions of application. The valences of the vertices in the graph-theoretic representation of the bridge system are the same whether or not we could also travel between two parts of town via boat or whether a bridge was blocked. The valences of the vertices is determined by the graph. Although we can appropriately make inferences in both directions when the conditions of application hold (from the non-tourability of Königsberg to the existence of at least one vertex with an odd valance and vice versa), the target is only sensitive to the conditions of application in one direction. Granting that we take explanation to differ from mere prediction in providing information about dependencies, the application of the graph-theoretic model can explain the non-tourability of Königsberg’s bridge system in terms of the existence of a vertex with an odd valence, but not vice versa.

The reason that conditions of application of the model are easily overlooked in this case is that there are closely related explananda that are less directly about a physical system such as Königsberg’s bridges and, when pushed, eventually not about a physical system at all but about the mathematical graph.¹⁰ For example, Lange [24, p. 14] takes the explanandum to rule out the use of boats.

Likewise, the ‘law’ that a network lacking the Euler feature is non-traversable has no conditions of application but helps to explain why Jones failed in attempting to traverse Königsberg’s bridges. Jansson might reply that the law’s conditions of application include (for instance) that the bridges are the only way to get from one Königsberg island to another region of land—that there are no ferryboats, for instance. After all (on this suggestion), had there been ferryboats, then it would have been possible to traverse all of the bridges, each exactly once, simply by crossing a bridge and then taking a ferryboat to the start of the next bridge. (And if there had been ferryboats, then the bridge arrangement would have been no different—exactly the asymmetry that Jansson emphasizes.) However, this suggestion fails to save Jansson’s proposal: the absence of ferryboats is not a condition of the law’s application because the explanandum is the impossibility of traversing (or the failure to traverse) each bridge exactly once by a continuous, landlocked path (etc.). To use ferryboats to ‘traverse’ the bridges would be cheating. So even if there had been ferryboats, it would have been impossible to traverse the bridges in the requisite way. The law has no conditions of application to the relevant sort of bridge traversal.

What Lange is suggesting is that there is an explanandum (or maybe the right explanadum) that rules out the use of alternative means of travelling between the landmasses of Königsberg. I agree that this is a perfectly legitimate explanandum but it does not remove the need for conditions of application of the explanatory model. After all, it is still an assumption here that the bridges are such that they can be crossed, etc. If they are not then the graph theoretic treatment of the actual bridge system again fails to be apt for the question at hand. To avoid any conditions of application we could try to abstract even further and define the explanandum of interest to be whether a system with the layout of Königsberg’s bridge system could be traversed in the suggested way setting aside any actual physical obstacles to undertake such a tour. However, this type of explanandum is best understood as a question directly about what explains the non-traversability (in a mathematical sense) of the graph typically associated with Königsberg’s bridge system rather than a question about the possibility of making a certain journey across the physical Königsberg.

Here, I have been focusing on explanations of physical facts and strictly speaking intra-mathematical explanations (where both the explanans and the explanandum are mathematical) fall beyond the scope of what I have tried to address. There are good reasons to treat them differently. To have a potential intra-mathematical explanation, we would expect to look at the details of the proofs for the two directions and whether they are explanatory or not. This will be a completely different explanation from the explanatory model that merely makes use of graph theory that we have discussed so far. However, it will bring out further assumptions that were previously hidden by our focus on a specific bridge system. In particular, the proofs hold under the assumptions that we are dealing with connected systems (the graph associated with Königsberg’s bridge system is connected). Whether a graph has an Eulerian cycle (in the case of an application to a specific bridge system, whether it is round-tourable in the way specified earlier) is sensitive to whether or not the graph is connected. However, whether a graph has only even vertices is not sensitive to whether the graph is connected or not.

The case that I have discussed so far is deliberately simple. However, I hope to have shown how several difficult philosophical issues about non-causal explanation arise even for simple cases. In general, it is not simple to determine the appropriate conditions of application of a model or a law and whether the target is sensitive to violations of those conditions. For example, the question of whether symmetries explain conservation laws, conservation laws explain symmetries, or neither explains the other, can be treated in a similar way but here the assessment involves questions about dependence that we do not have immediate access to.¹¹ In the next section, I will consider how conditions of application play a role in determining directionality in a less straightforward, but much discussed, case of explanation by network models.

5. Small-world network models

In this section, I would like to consider an objection to my account similar to the one raised by Lange to the Königsberg’s bridges case in the previous section. For some uses of network model explanations, it might seem that there are no particular conditions of application. Rather, the system under investigation might be thought to simply instantiate the relevant network properties.

Certain ways of talking fit well with such a view. For example, it is common to find discussions that refer to the small-world properties or architecture of physical systems. For example, Watts & Strogatz [3, p. 442] conclude their article by noting that ‘[a]lthough small-world architecture has not received much attention, we suggest that it will probably turn out to be widespread in biological, social and man-made systems …’. Of course, such ways of talking do not in and of themselves commit authors to any specific view about the relationship between the explanatory model and the explanatory target.¹² However, if we take the above ways of talking at face value then it is tempting to take the explanatory target system to simply instantiate the relevant network (or topological) properties. For example, I take this view to be the one expressed by, for example, Huneman [27, p. 119] when writing that ‘… in topological explanations, the topological facts are explanatory, and not the various processes that in nature instantiate variously these properties’.

In combination with a dependence view of explanation the consequence of such a view is that we should expect to find all the relevant explanatory counterfactuals simply by paying attention to dependence of type 2 (the dependencies internal to the model) because the explanatory target systems simply instantiate the relevant network (or topological) properties. I have suggested that we need to pay attention to what makes it apt to apply the relevant models in order to understand the directionality of the explanations of physical facts given using these models. This means that I think that we have reason to resist taking the explanatory target systems to simply instantiate the relevant network properties.

To see what this looks like in practice, let us consider an example from Watts and Strogatz [3].¹³ Watts & Strogatz [3] start with a regular ring lattice with a fixed number of vertices and a fixed number of edges per vertex. This ring lattice is then rewired with a probability p (so that p=0 leaves the perfectly regular ring lattice intact and p=1 results in a random network). The characteristic features of the resulting networks understood as a function of p is the clustering coefficient (informally the ‘cliquishness’ of the graph) and the characteristic path length (capturing the average number of edges that have to be traversed in order to reach any node in the network). Small-world networks are characterized by low characteristic path lengths and high clustering. Watts & Strogatz [3] make use of these notions to understand how the structure of networks influences the dynamics of disease spread. In particular, they find that the infectiousness of the disease (modelled as the probability that an infected individual infects a given healthy neighbour) required in order for the disease to infect half of the population decreases rapidly for small p. Informally, as we move away from a perfectly regular ring lattice, the infectiousness required in order for a disease to end up affecting half the population goes down rapidly. Finally, for diseases that are sufficiently contagious to infect the entire network population, the time to complete infection of the population closely follows the characteristic path length. The conclusion drawn is that even intuitively minor deviations from perfectly regular networks has a dramatic effect on the spread of infectious diseases. Moreover, the dynamics is taken to be able to be understood via the network structure.

Thus, infectious diseases are predicted to spread much more easily and quickly in a small world; the alarming and less obvious point is how few short cuts are needed to make the world small.

Our model differs in some significant ways from other network models of disease spreading. All the models indicate that network structure influences the speed and extent of disease transmission, but our model illuminates the dynamics as an explicit function of structure […], rather than for a few particular topologies, such as random graphs, stars and chains. [3, 442]

On one way of understanding this discussion, it seems be an assertion that in order to understand some aspects of disease spread all we need is understanding of certain network properties. However, I think that this conclusion should be resisted.

Watts & Strogatz [3] are clear that their discussion is focused on a certain highly idealized model of disease spread. In order to take the dynamics of disease spread to depend on the highly mathematical features of network structure we also need to, on my account above, worry about how the dynamics of disease spread depends on these idealizations. As in the case of Königsberg’s bridges, I think that these conditions of application hold the solution to account for why we are inclined to, and correct to, take the structure to possibly explain the dynamics of disease spread in the cases where the model applies but not vice versa. If we ignore the conditions of application, we again face a situation where we can make inferences in seemingly non-explanatory directions. For example, we could make the inference from the functional form for the time for global infection to the functional form for the characteristic path length. Yet, this inferences does not look explanatory.

Without invoking some special notion of mathematical, abstract, metaphysical, etc., dependence we can now try to identify the direction of explanation by asking questions about the dependence of the explanatory target on the conditions of application. For example, Watts & Strogatz’s [3, p. 441] idealized model assumes that we introduce a single sick individual into an otherwise healthy population and that infected individuals are removed after one unit of time (by death or immunity). Are properties of network structure, say the functional form for the characteristic path length, sensitive to when these modelling assumptions hold or not? The answer is that the relevant properties of network structure are completely insensitive to whether or not we are dealing with a homogeneous population of healthy individuals (barring the sole infected individual). This simply is not something that features such as the characteristic path length capture. Is the explanatory target, the dynamics of disease spread, sensitive to changes in these assumptions? The answer is very plausibly yes. For example, if we do not start from a homogeneous healthy population (with the exception of the one infected individual) then we can expect the dynamics of disease spread to look different. For example, consider the effect on the spread of a new strain of an infectious disease if the population has previously been infected with an earlier strain of the disease which provides immunity to the new mutation. As Leventhal et al. [28, p. 7] note, ‘the initial strain modifies the residual network of susceptibles’ and the spread of infectious disease should be expected to be sensitive to this. Leventhal et al. [28] argue that here heterogeneity in contact structure suppresses the spread of a new strain.

If we take the explanation of the dynamics of disease spread provided by Watts & Strogatz [3] to simply be one where the dynamics is understood purely in terms of the network structure then this looks like a potential challenge to their conclusions. However, on my view this would be the wrong conclusion to draw. Rather, the broader understanding of the simplified model (including the conditions of application) is what allows us to identify as explanatory certain inferences that we can make when the model applies (taking other inferences to be non-explanatory). Because the explanatory target of the dynamics of disease spread is sensitive to violations of the conditions of application the Watts & Strogatz [3] model can be regarded as explanatory by providing part of the story about what infectious disease spread depends upon.

If my argument in this article is correct, understanding the assumptions and limitations of network models is not only important in order to avoid mistakenly applying the models in cases where they fail to apply. To understand how the target phenomena depend on the assumptions of the network models is key to understanding why the inferences drawn using network models sometimes count and sometimes fail to count as explanatory at all.

6. Conclusion

I have argued that if network explanations are (sometimes) examples of a broader class of non-causal explanations then the challenge of addressing long-standing problems of distinguishing prediction from explanation that are otherwise resolved in causal terms require new solutions in these cases. Many philosophical suggestions postulate directed metaphysical notions to address this problem. I have argued that an account of scientific explanation that includes the conditions of model aptness as part of the explanation can address the problem of directionality without facing the same difficulties as competing approaches.

Data accessibility

This article has no additional data.

Competing interests

I declare I have no competing interests.

Funding

No funding has been received for this article.