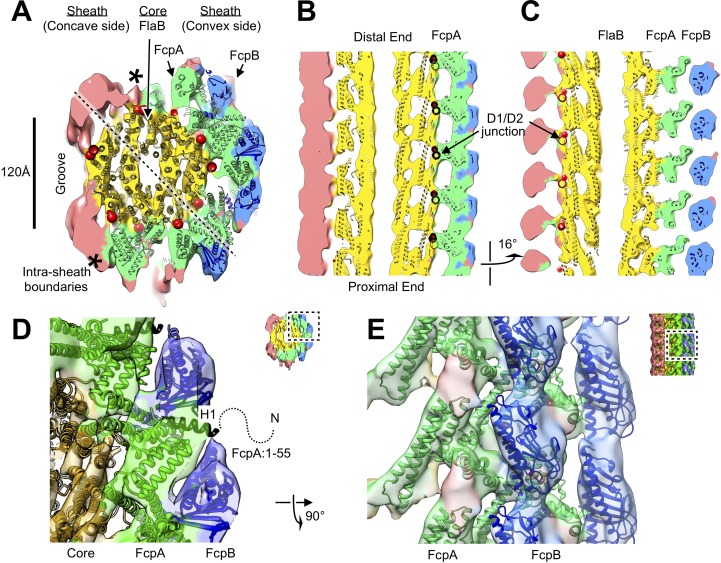
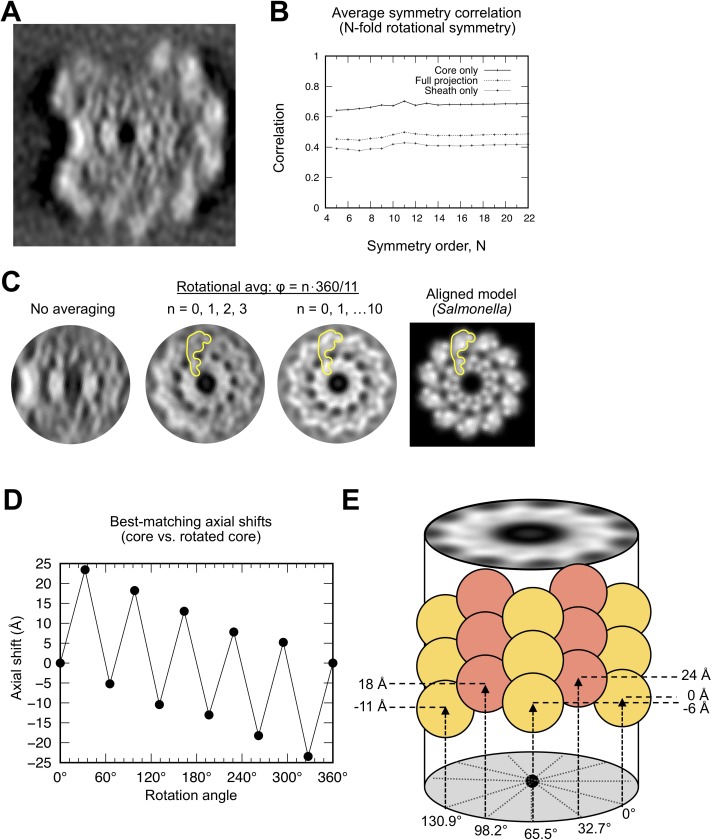
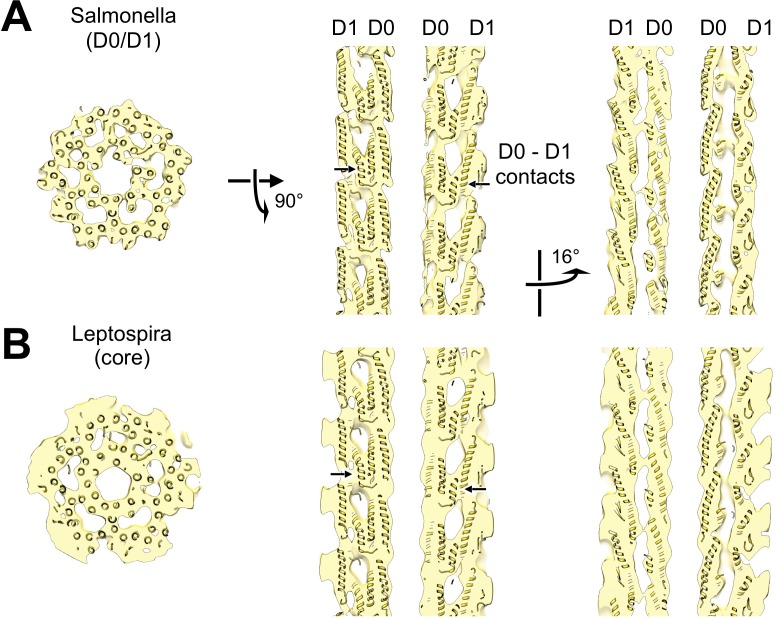
Figure 3. Atomic model of the core and sheath regions of the L. biflexa flagellar filament obtained by docking X-ray crystal structures into the cryo-EM map.
(A) Cross-sectional slice of the filament density map isosurface with fitted models of the pseudo-symmetric core assembly (yellow ribbons) and two sheath components, FcpA and FcpB, which localize to the filament outer curvature. Six FcpA protofilaments (green ribbons) directly contact the core and support an outer layer consisting of four FcpB protofilaments (blue ribbons). Asterisks denote boundaries between FcpA and inner curvature density (red). Red markers denote the location of the junction between the modeled D1 α-helical domain of FlaB and the species-specific insertion that substitutes for the D2/D3 outer domains found in Salmonella spp. FliC (flagellin) but not in Leptospira spp. FlaB. (B) Longitudinal slice through the filament center, corresponding to the dashed line in A, showing the central channel surrounded by the core and sheath layers. The major interface region between FcpA and the core coincides with this insertion. (C) A 16° rotated view of the map in B showing core-sheath contacts at the site of the FcpB insertions on the opposite side of the filament (concave side); identity of the sheath protein (red) is unassigned. (D) Close-up cross-sectional view of the averaged filament map showing X-ray model fits of FcpA and FcpB in the outer curvature sheath region. (E) Close-up view of the averaged filament map rotated 90° relative to the view in D showing X-ray model fits.
Figure 3—figure supplement 1. Structure model of Leptospira FlaB by homology modeling and sequence alignment.
(A) Schematic of aligned sequences of Salmonella FliC (top) and Leptospira FlaB (bottom), indicating assignments for subdomains D0 and D1. (B) Axial view of the Salmonella flagellar filament structure (left) and side view of the component FliC structure (right; PDB ID 1UCU Yonekura et al., 2003) depicting the locations of subdomains D0-D3. (C) Corresponding views of the modeled Leptospira FlaB core assembly.
Figure 3—figure supplement 2. Centroid angular positions of fitted FcpA and FcpB models match an 11-protofilament pseudo-helical lattice.
(A) Filament cross-sectional view showing centroid positions of fitted FcpA models (green spheres) and their angular position (green lines) with respect to the middle of the central channel (white sphere). Overlaid are predicted angular positions (black dashed lines) for symmetric helical lattice sites of the given symmetry type (n = 10, 11, or 12 protofilaments). Root mean squared angular deviations between centroid and symmetric angular positions (σ) are smallest for the 11-protofilament case. (B) Plots of FcpB centroid positions, as in A, indicating best agreement with an 11-protofilament binding pattern.
Figure 3—figure supplement 3. Identification of six similarly arranged FcpA protofilaments in the flagellar filament sheath.
(A) Schematic depicting locations of symmetry-related ‘slab’ volumes defined within the filament sheath layer, and corresponding docked FcpA sites. Volume slabs are rotated in progressive increments of 360°/11 = 32.7° about an axis tangent to a curve running through the filament center (which corresponds to the filament helical axis, for a straightened filament). (B) Two-dimensional projections (left column) of the slab volumes in A, revealing six rows (‘PF1’ – ‘PF6’) of distinctive ‘V’-shaped features consistent with the size and shape of FcpA monomers (green outlines) docked onto the core surface. V-shaped features are absent (red dashed outlines) from symmetry-related locations in remaining volume slabs (‘PF7’ – ‘PF11’), indicating a discontinuity in the corresponding pseudo-helical array of FcpA molecules identified by computational docking studies (Figure 3). In the middle column, density features are aligned with each other by applying axial shifts corresponding to the pseudo-helical lattice parameters, and circular masks are applied to isolate features corresponding to non-overlapping regions of individual FcpA subunits. The right column shows consensus averages of identified ‘FcpA’ sites, used as references for cross correlation comparison with the masked areas in the middle column. To avoid spuriously high cross-correlation values, the reference image for each protofilament is resampled to exclude the identified ‘FcpA’ site from that same protofilament, if present. Cross-correlation scores between protofilament regions and the references reveal a strong resemblance of the six identified FcpA sites to the consensus features (cross-correlation ≥0.69). In contrast, cross-correlation of the remaining five sites to the references is much lower (≤0.39), suggesting that FcpA is either absent or binds in a very different configuration. Note that the much lower correlation between PF7-PF11 sites and the references (B), compared with the PF1-PF6 sites, cannot be explained by artifacts due to the ‘missing cone’ of Fourier data in the subtomogram average (due to preferred sample orientation); the range of axial rotations spanned by the PF1–PF6 sites is more than 180°, encompassing all possible orientations of the missing cone. Thus, missing cone artifacts seen in any FcpA subunits bound to PF7-PF11 would be comparable to those in PF1-PF7.
Figure 3—figure supplement 4. Asymmetry of inner and outer sheath density features in wild-type Leptospira filaments.
(A) Comparison of sheath density features for different lateral cross sections of the wild-type Leptospira subtomogram average, related by pseudo-helical symmetry. The core region is delineated by gold dashed lines; bounds for FcpA and FcpB regions are denoted by green and blue dashed lines, respectively. For sites on the outer curvature where we identified occupancy for both FcpA and FcpB (top two panels), two distinct density layers are observed corresponding to the two components. Note the presence of radial spoke-like features as well as large, characteristic voids (dark regions) corresponding to the FcpA layer. For sites on the inner curvature (fourth and fifth panels), sheath density features have a distinctly more globular character (note the absence of spoke-like features or large voids). For the FcpA site where the FcpB locus was vacant (third panel, ‘No FcpB’), the features are ‘smeared’ in the horizontal direction due to resolution anisotropy (see Figure 2—figure supplement 5). However, note that characteristic features of the FcpA/FcpB sheath layer located on the opposite side of the core can still be distinguished in this panel (compare the right-hand sides of panel 3 and panels 4–6)– thus indicating that individual subunit features can still be resolved, consistent with the estimated range of anisotropic resolution values (worst resolution in the sheath ~8–35 Å; see Figure 2—figure supplement 5). (B) Axial cross-section of the wild-type Leptospira subtomogram average, with arrows indicating the cross-section directions for the six panels in A. Gold, green and blue dashed lines denote the identified core, FcpA and FcpB regions for our model.
Figure 3—figure supplement 5. Symmetry analysis of the Leptospira core indicates an 11-protofilament architecture.
(A) Projected filament cross section of a 52Å-long segment of the wild-type L. Biflexa flagellar filament. (B) Plot of the averaged cross-correlation between the image in A and N rotated copies of itself, corresponding to rotations of 1*360°/N, 2*360°/N, … (N-1)*360°/N about the filament center. Thus, for an image containing an 11-fold symmetric feature, the averaged cross-correlation value will be highest for symmetry order N = 11. Systematically varying N in this calculation reveals a maximum corresponding to 11-fold radial symmetry, matching the symmetry of the Salmonella flagellum. Cross-correlations were computed for the entire image (‘full projection’) as well as masked sub-regions corresponding to the core (‘core only’) and sheath (‘sheath only’). All three of these calculations yield a maximum score for N = 11. (C) The 11-fold symmetry operator identified in B was used to average the projected map, reducing the effects of the missing wedge and substantially improving molecular features. Leftmost panel shows the original core region, center-left panel shows the result of adding four symmetry-related copies (N = 11; Φ = 0*360°/11, 1*360°/11, 2*360°/11, 3*360°/11) and center-right panel shows the result of adding 11 symmetry-related copies (resulting in an 11-fold symmetric image). Features in the averaged images (yellow shape) resemble the projected D0/D1 subdomain within a projected Salmonella flagellar filament cross section (rightmost panel; synthetic image derived from PDB ID 3A5X). (D) Results of three-dimensional cross-correlation analysis between the wild-type sub-tomographic average volume and rotated copies of itself. For each rotation value (Φ=0*360°/11, 1*360°/11, … 11*360°/11), a volume copy was rotated about an axis running through the center channel and masked to exclude all but the core region of a single 52 Å axial repeat. A 3D cross-correlation map was then computed between the resulting volume and the original reference, and the axial shift described by the top-scoring peak was plotted for each Φ rotation value. The resulting graph describes a staggered pattern of helical subunit positions closely matching the 11-start helical symmetry observed in several other reported bacterial flagella structures (Namba et al., 1989; Wang et al., 2017). The estimated pseudo-helical parameters (~26 Å helical pitch,~5.5 subunits per turn) closely match helical parameters established for several other flagellar filaments (i.e. Salmonella:~25.5 Å – 27 Å helical pitch, 5.4x – 5.5x subunits per turn).
Figure 3—figure supplement 6. Structural homology between the D0/D1 core region from a synthetic map of the Salmonella flagellar filament and the core region of our wild-type Leptospira flagellar filament subtomogram average volume.
(A) Axial and lateral cross sections of the Salmonella flagellar filament from an atomic model (Yonekura et al., 2003) rendered at 12 Å resolution. (B) Corresponding cross sections of the aligned Leptospira flagellar filament subtomogram average volume, after 11-fold symmetry averaging.