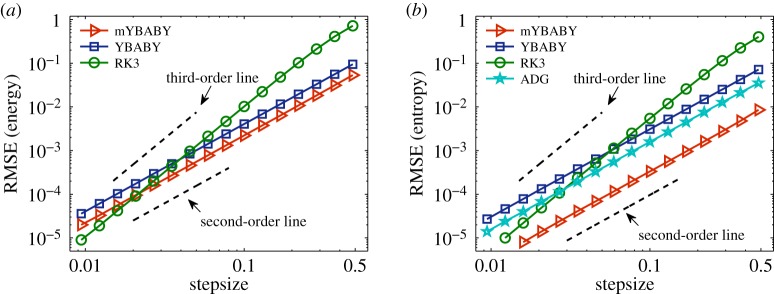
Figure 2.

Double logarithmic plot of the root-mean-square error (RMSE) (4.1) in the total energy (3.1) (a) and entropy (b) against stepsize by comparing the two split GENERIC integrators introduced in this article with the third-order Runge–Kutta (RK3) method and the average discrete gradient (ADG) method, which conserves the total energy exactly (i.e. up to machine precision) and thus is only included in comparisons of the entropy production, with a damping rate of γ = 0.01 and a total simulation time of T_s = 200 in a standard setting of a damped harmonic oscillator as described in §4a. The stepsizes tested began at h = 0.0094 and were increased incrementally by 30% until around h = 0.5. Note that, with this set of parameters, the damped harmonic oscillator is ‘underdamped’ (i.e. the position of the particle oscillates around zero with the amplitude exponentially decreasing to zero) and the associated period is T_p ≈ 2π. Dashed black lines represent the second- and third-order convergence as indicated. (Online version in colour.)