Abstract
Terahertz (THz) imaging and optical coherence tomography (OCT) provide complementary information with similar length scales. In addition to OCT’s extensive use in ophthalmology, both methods have shown some promise for other medical applications and non-destructive testing. In this paper, we present an iterative algorithm that combines the information from OCT and THz imaging at two different measurement locations within an object to determine both the depth of the reflecting layers at the two locations and the unknown refractive index of the medium for both the OCT wavelengths and THz frequencies. We validate this algorithm using a silicone test object with embedded layers and show that the depths and refractive index values obtained from the algorithm agreed with the measured values to within 3.3%. We further demonstrate for the first time that OCT and THz images can be co-registered and aligned using unsupervised image registration. Hence we show that a combined OCT/THz system can provide unique information beyond the capability of the separate modalities alone, with possible applications in the medical, industrial and pharmaceutical sectors.
1. Introduction
Optical coherence tomography (OCT) and terahertz (THz) imaging both provide the potential for sub-surface characterization of materials and biological tissue that may advance medical, pharmaceutical and industrial applications [1–3].
OCT is sensitive to the gradient of the refractive index at near-infrared wavelengths which, in biological specimens, depends on scattering from structural arrangements of cells and organelles [4], whereas THz imaging, which uses much longer wavelengths, is much more dependent on absorption mechanisms than scattering [5,6]. THz can detect, for example, variations in hydration [7–9] while OCT offers clear indications of the structure and morphology of the specimen [3]. Furthermore, THz imaging and OCT both provide 3D information over a similar size, scale and depth; both provide diagnostic information correlated to histopathology [10,11] and both can use the same ultrafast laser source for signal generation. The complementary nature of the two imaging techniques and their common use of ultrafast laser systems poses the intriguing question: could they be combined into a single imaging system?
There are several common applications where the two techniques are currently being researched or applied separately. The penetration depth of THz and OCT, which are both on the scale of millimeters or less in most materials, including biological tissues, tends to guide the nature of these applications. Some of the areas showing potential are near-surface (epithelial) or intra-operative cancer imaging [12–15], skin hydration changes [16,17], corneal hydration [18,19], pharmaceutical quality control [20,21] and cultural heritage [22–27]. There are possible applications where combining the techniques and overlaying complementary properties of structure and morphology from OCT with functionality and hydration properties from THz imaging, may lead to improved diagnostic sensitivity and specificity. For example, in ophthalmology, this could lead to an improvement in the assessment of certain eye diseases such as Fuch’s dystrophy [28], a degenerative condition of the corneal endothelium which causes swelling of the cornea; or the combined technique could aid clinical decisions regarding corneal grafts [29].
Previous researchers have proposed that imaging a sample using THz and OCT may be of benefit for diagnosis [30]; however, as yet there have been no studies that combined the two. For example, Chernomyrdin et al. [14] used both OCT and THz to examine malignant brain tissue, but did so separately and did not use either OCT to inform the THz properties, or vice versa. They do propose ‘multiplexing the information’ without providing methods to do so. Taylor et al. [31] discuss the potential of using THz and OCT for imaging the cornea to provide structure and hydration, but again, do not discuss the way in which the OCT and THz data can be combined to inform each other, and enhance the information that can be obtained. This study is the first where the information from OCT and THz has been combined to provide enhanced information that is not available using either technique independently.
In this study, we present an algorithm for using the time-of-flight information obtained from OCT and THz images of the same areas as a way to determine the depth of a layer within an object and the refractive index values at THz frequencies and OCT wavelengths. The algorithm uses measurements of OCT and THz at two locations within the object with two different depths to give the depths of the layers and the refractive index values. The algorithm was tested on OCT and THz images of a silicone test object with titanium dioxide (TiO2) scatterers as contrast agents to create reflecting layers at different depths. Silicone has been used previously as a tissue-equivalent test object for OCT [32,33] and we verify its use with THz imaging in this study. The aim was to evaluate the algorithm to determine the accuracy with which it can provide both depth and refractive indices and examine factors that affect its performance.
Further, we demonstrate for the first time that OCT and THz images can be processed to give quantitatively accurate distance information using this algorithm. The images can then be co-registered to overlay the complementary OCT and THz information. Finally, we show that it is possible to determine the depths of layers at other locations in the images using the information obtained from the algorithm, assuming a uniform refractive index throughout the medium. The ability to overlay co-registered THz and OCT images and establish the depths of layers and properties of the materials may support clinical and non-destructive testing assessments for improved pathological decisions, and improved non-destructive characterization of materials.
2. Methods
2.1. Development of the tissue-equivalent test object
A test object was developed that provided tissue-equivalent contrast at optical wavelengths and was an appropriate material in terms of absorption and refractive index for THz imaging. Silicone is frequently used in OCT imaging as a test object due to its low scattering properties and its high transparency in the near-infrared. To test whether silicone was suitable as a THz test object material, we used THz spectroscopy to determine its refractive index (see section 2.1.2). The silicone test object was formed by mixing a silicone base liquid with a hardener according to the manufacturer’s recipe (ELASTOSIL RT 601 A/B, Wacker Chemie AG, Germany) [34].
2.1.1. Embedded objects using a contrast agent
Titanium dioxide (TiO2) powder, which is frequently used as a scattering agent at near-infrared wavelengths [35], was tested to determine whether it could create a refractive index boundary that could be detected using THz imaging. After testing a variety of concentrations, it was found that 2% by weight gave absorption and refractive index changes that were detectable with both THz and OCT. The TiO2 powder was added to silicone at 2% concentration to form a layer approximately 1 mm thick. After setting, a square shape and an approximate rectangle shape were cut from the TiO2 layer. The surfaces of both the square and the rectangle were not flat but had shapes that changed across the profile to provide a variety of depths. These shapes were then embedded into the silicone test object before it set at a depth of just over 1 mm. The final dimensions were 26.6 mm × 27.4 mm × 3 mm (Fig. 1(a) ).
Fig. 1.
(a) Photograph of the front surface of the silicone main test object. The white areas are the embedded highly-scattering silicone-TiO2 contrast objects. Areas A, B and C were the locations where the depth of the silicone back interface was calculated and represent the full thickness of the test object. Areas D and E were the locations where the depth of the embedded square was calculated. The red dotted line represents the profile region along which the depth profile of the rectangle was calculated. (b) An en-face THz image, which takes the absolute value of the integral of the reflected THz pulse over a time range of 12 ps for each time-domain waveform and assigns that value to the pixel to form the 2D image and (c) several of the OCT en-face images manually stitched together. The image property used for each pixel in the OCT image was the maximum of the log intensity of the signal returned from the embedded objects.
In a combined system, we would envisage THz imaging with normal incidence [36] or very near normal incidence [37] similar to the OCT set up. However, for this study, the THz imaging system used had a 30° angle of incidence and a larger scanning range of 20 mm, compared to 5 mm for the OCT system. For these reasons, we designed a test object with multiple embedded objects that were similar in size to the field of view of the THz system. For OCT imaging the test object was moved after each image acquisition so that relevant sections could be imaged with OCT that overlapped with the THz image. The regions of the test object that were imaged using both THz and OCT are shown in Fig. 1(a), while Fig. 1(b) and Fig. 1(c) show the THz and OCT en-face images of the test object, respectively.
2.1.2. Refractive index of the silicone test object at THz frequencies
The refractive index of the silicone test object was measured at THz frequencies using a commercial THz time domain system (TeraPulse4000, Teraview Ltd, Cambridge, UK). This system was used for both spectroscopy and imaging of the test object. The system provides a broadband pulse with a range of frequencies 0.06 - 4 THz. Since the refractive index of silicone varies as a function of THz frequency, the measured refractive index was determined using a weighted mean refractive index to represent the bulk properties of silicone across this frequency range. The weighting was based on the spectral amplitude of each frequency component of the pulse, as determined by spectral analysis. The bulk refractive index for the silicone across this frequency range determined, by transmission spectroscopy on a piece of silicone with known thickness, was 1.53 ± 0.08.
2.1.3. Refractive index of the silicone test object at OCT frequencies
OCT measurements were performed using a fiber-based, swept-source polarization-sensitive (PS) OCT system with a standard bench-top configuration. The light source used was a wavelength-swept laser (Axsun Technologies, Bellerica, MA, USA), centered at 1310 nm, with a full sweep range of 130 nm at a 50 kHz sweep rate [38,39]. For comparison of the refractive index obtained for the algorithm for the OCT wavelengths, a calibrated refractive index of the silicone was measured by using a known thickness of several millimeters and measuring the optical path length. The refractive index was found to be 1.43 ± 0.04, which agrees with published values of 1.4 [32]. Small differences may arise based on the formulation of the silicone.
2.2. Imaging the test object
2.2.1. THz imaging of the silicone test object
We used the imaging module of the Terapulse4000 to collect a 3D data set from the test object. The imaging module raster scans a THz pulse over a defined area (x, y) in which each pixel contains the reflected time-domain signal (amplitude and phase). The THz pulse was incident on the sample at 30° and focused into the sample using f2 optics. The THz images were scanned over an area of 20 mm by 20 mm with a sample spacing of 0.2 mm. The front surface of the test object (the surface at which the THz was incident) was placed at the focal point and then the z-position of the test object was focused by maximizing the reflected signal from the embedded square TiO2 object which is approximately 1 mm deep within the silicone. Thus a three-dimensional dataset (x, y, t) is obtained where the third dimension is time which, if the refractive index of the sample is known, can be converted into a spatial dimension. A reference measurement is acquired from a flat gold coated mirror, and is deconvolved from the sample pulse prior to further analysis of the signal. Table 1 compares THz imaging characteristics to OCT.
Table 1. Comparison of the OCT and THz imaging systems.
| Imaging System | Wavelengths | Frequency | Lateral Resolution | Axial Resolution |
|---|---|---|---|---|
| OCT imaging | 1310 nm | 229 THz | 25 µm (@1310nm) | ∼11 µm (@1310nm) |
| THz imaging | 5000 µm – 75 µm | 0.06 THz – 4 THz | ∼75 µm (@ 3 THz) | 30 µm (@ 3 THz) |
2.2.2. OCT imaging of the silicone test object
The OCT system had a field of view of 5 mm by 5 mm. The angle of incidence for the OCT system was perpendicular to the surface of the test object. The test object was mapped in the x-y direction in steps of 5 µm. In the z-direction, 1152 pixels were obtained corresponding to an optical path length of 8 mm in air. Due to the smaller field of view for OCT, the test object was imaged at several locations around the boundaries of the embedded square and rectangle (see Fig. 1(c)). The intensity value obtained from processing the OCT images is used for all images and data analysis. The resulting processed images were used to calculate the thickness of the silicone and the depth of the embedded object.
2.3. Image analysis and registration
2.3.1. Determining depth and refractive index values for normal incidence of OCT and THz
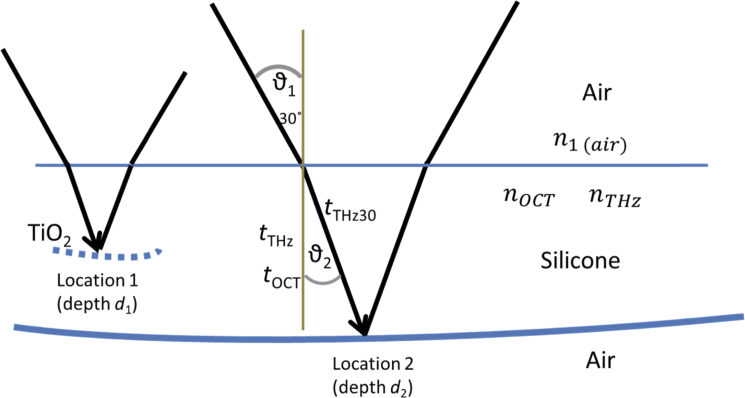
Given two locations, 1 and 2, with unknown depths d1 and d2, (as illustrated in Fig. 2 ) we can calculate d1 and d2, and the unknown refractive indices, nOCT, and nTHz of the material using OCT and THz measurements at these two locations. THz and OCT measurements at each of the locations 1 and 2, provide four known values, tOCT1, tOCT2, tTHz1, tTHz2, where t represents the ‘time-of-flight’ for the time travelled by the electromagnetic radiation for the OCT measurement and the THz measurement to the reflecting surface within the material, assuming normal incidence. In the measurements performed, the THz signal was not normally incident on the silicone, and the method to account for this is given in section 2.3.2. These four values can be used to solve four simultaneous equations that relate to the depth d1 and d2 and the refractive index in the optical regime (nOCT) and the THz range (nTHz). The simultaneous equations were obtained as follows:
| (1) |
| (2) |
| (3) |
| (4) |
Fig. 2.
Illustration of the THz pulse incident on the front surface of the silicone at 30° and refracted due to the refractive index nTHz before being reflected from the embedded TiO2 layer at location 1 and silicone back interface at location 2. The angle ϑ2 is unknown in this case since it depends on nTHz, and nTHz is assumed to be unknown. The time-of-flight for a normally incident THz pulse is shown as tTHz, while the measured time-of-flight of the THz pulse, incident at 30° is tTHz30.
Rearranging Eq. (1)–(4) gives four simultaneous equations with four unknowns:
| (5) |
| (6) |
| (7) |
| (8) |
Solving these four simultaneous equations yields the depths d1 and d2 of the two locations, and the refractive index nOCT and nTHz for both OCT wavelengths and THz frequencies. For this study the equations were solved using Matlab’s (Matlab, version 14, Mathworks, Natick USA) fsolve function.
2.3.2. Correction of THz time-of-flight for non-normal THz incidence
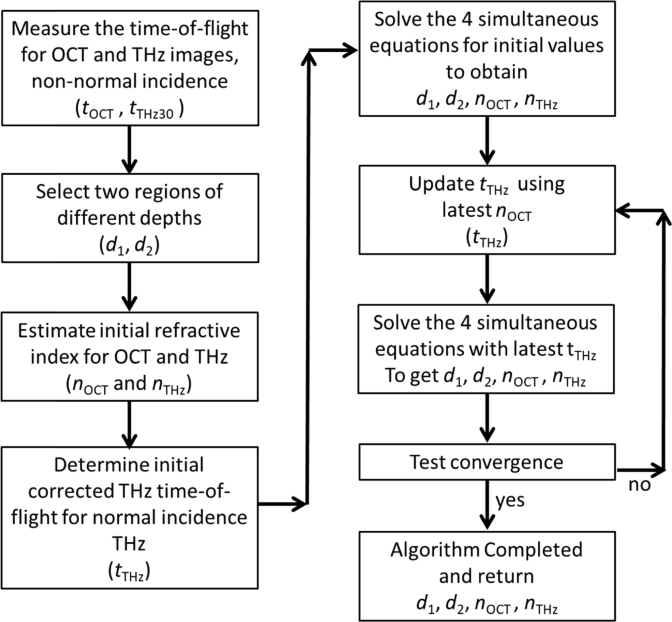
Unlike the OCT signal, which is at normal incidence to the surface, the THz pulse is incident at an angle of 30° (ϑ1). The implication of this is that the measured time-of-flight for the THz pulse, tTHz30 must be corrected to obtain the time-of-flight for normally incident THz radiation, tTHz before being input into Eq. (6), (7) and (8). In order to use Snell’s law to determine tTHz at normal incidence, the angle ϑ2 must be known (Fig. 2). However, determining ϑ2 requires knowledge of the refractive index, which we assume is not known in this case. Instead an iterative approach can be used to estimate ϑ2 using an initial first guess for nTHz that then allows tTHz to be calculated from tTHz30 with knowledge of tOCT and an initial guess for nOCT. This updated tTHz is then used in Eq. (6)–(8) to determine the next iteration of depth values and the refractive index values nOCT and nTHz. The updated nTHz and nOCT are used to improve the determination of tTHz from tTHz30. The procedure is repeated iteratively until the values of tTHz, and subsequently d1, d2, nOCT and nTHz converge to a desirable limit. The mathematical relationship between tTHz and tTHz30 is shown in Eq. (9)–(12), and the full algorithm is shown schematically in Fig. 3.
Fig. 3.
Schematic flowchart of the iterative algorithm to determine the depth and refractive index values from two locations using OCT and THz images, accounting for the angle of incidence of the THz pulse if it is non-normal. The algorithm assumes initial values for the refractive index at OCT wavelengths and THz frequencies and successively updates these and determines the depth of the layers simultaneously.
From Snell’s law we have
| (9) |
where nair = 1 and ϑ1 for the THz pulse is 30°.
Using the trigonometric relationships and substituting for ϑ2 we obtain
| (10) |
Given that the depth of a location is the same for THz as it is for OCT, we have
| (11) |
Substituting Eq. (11) into (10), we determine the series for tTHz
| (12) |
Equation (12) can be solved iteratively by inputting an initial first guess for the nOCT and using the iterative previous value of tTHz(n) as well as the known value of tOCT measured from the two locations. The solution tTHz was successively updated until an acceptable convergence was reached, defined arbitrarily as the limit in which the change from the previous value was less than 0.0001 ps. In the study we performed, this was typically after 4-5 iterations. As mentioned previously, the adjusted value for tTHz was then used to solve Eq. (5)–(8) and the procedure repeated, using the updated refractive index for THz and OCT in Eq. (11) and (12) until the refractive index and depth from Eq. (5)–(8) converge. The flow of the full algorithm is given in Fig. 3.
2.3.3. Calculation of layer depths in the silicone using combined THz and OCT
The iterative method of obtaining the depth and refractive index outlined in sections 2.3.1 and 2.3.2 was applied to measurements on the silicone object using five different regions labelled A, B, C, D and E in Fig. 1. Regions A, B and C had no buried layers, so the reflected signal at depth represented the full depth of the silicone and could be compared with a measured depth. Regions D and E had the embedded TiO2 square shape that led to reflections with shorter times-of-flight so it could be used to test the efficacy of the algorithm with a range of depth locations. All regions were 2.5 mm by 2.5 mm in the x-y direction. The actual thickness of the silicone at locations A, B and C was measured using a micrometer. The micrometer thickness measurements were repeated ten times in each of the three locations A, B and C and then averaged to give a mean measured silicone thickness at each location with a standard deviation of the mean.
To measure the depth of the embedded square, the test object was sliced into sections and viewed under a microscope at eight times magnification. By calibration of the microscope image, the distance from the front surface of the silicone to the front surface of the embedded square could be determined at 10 locations within region D and region E. These were averaged and a standard deviation obtained. The mean calculated depths and the refractive index values determined from the algorithm for these ten unique pair combinations are given in Table 2 compared to the measured values for all regions A-E along with a percentage difference between the two.
Table 2. Values of the depth and refractive index calculated from the iterative algorithm for each of the ten unique pair combinations for the 5 locations A, B, C, D and E. The mean of each value is calculated and presented with the standard deviation. These calculated values are compared to the measured values and the percentage difference between the measured and calculated is given in the bottom row of the table.
| Pair | Depth at location (mm) | Refractive index | |||||
|---|---|---|---|---|---|---|---|
| A | B | C | D | E | n OCT | n THz | |
| [A, B] | 3.137 | 2.966 | 1.423 | 1.493 | |||
| [A, C] | 3.115 | 3.145 | 1.428 | 1.509 | |||
| [A, D] | 3.132 | 1.299 | 1.418 | 1.502 | |||
| [A, E] | 3.116 | 1.296 | 1.418 | 1.517 | |||
| [B, C] | 2.954 | 3.155 | 1.430 | 1.499 | |||
| [B, D] | 2.975 | 1.305 | 1.420 | 1.487 | |||
| [B, E] | 2.960 | 1.302 | 1.419 | 1.502 | |||
| [C, D] | 3.145 | 1.291 | 1.427 | 1.510 | |||
| [C, E] | 3.129 | 1.289 | 1.427 | 1.525 | |||
| [D, E] | 1.292 | 1.297 | 1.408 | 1.524 | |||
| Mean Calculated Value | 3.125 ± 0.011 | 2.964 ± 0.009 | 3.143 ± 0.011 | 1.297 ± 0.011 | 1.296 ± 0.010 | 1.422 ± 0.007 | 1.507 ± 0.013 |
| Measured Value | 3.05 ± 0.04 | 2.87 ± 0.05 | 3.08 ± 0.06 | 1.26 ± 0.04 | 1.27 ± 0.04 | 1.43 ± 0.04 | 1.53 ± 0.08 |
| Difference (%) | 2.5% | 3.3% | 2.1% | 2.9% | 2.0% | −0.6% | −1.5% |
2.3.4. Factors affecting the performance of the algorithm
To understand the limitations and performance of the algorithm, we examined several factors that influenced the outcome of the final values. These were the depth of the locations, the refractive index values used for the initial guess, and the number of iterations for convergence. The effect of depth was examined by using a range of five depths, two shallower around 1 mm, and three deeper around 3 mm.
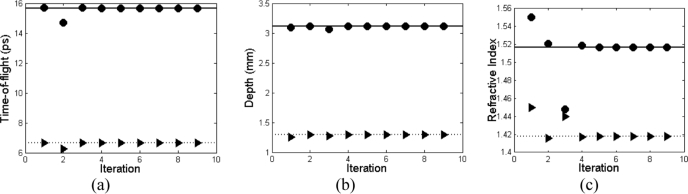
To understand the influence of refractive index initial starting values, we tested the algorithm with a range of starting points of nOCT ranging from 1.3-1.5, and nTHz from 1.4-1.7, which represented a range either side of the expected values. The results for this range of starting refractive index initial estimates are given in Table 3 . To observe the speed with which the algorithm converges with each iteration, we present a case study for pair-combination [A, E] where the values at each stage of the iteration are shown in Fig. 4 for 9 iterations compared to a line showing the convergence value.
Table 3. The impact of the initial starting values of the refractive index for OCT (nOCT) and THz (nTHz) on the outcome of the algorithm for the case example of pair combination [A,E]. A percentage difference was calculated for each value compared to the measured value. Note that the measured values for d1 and d2 are 3.05 mm and 1.27 mm respectively for regions A and E. The measured refractive index for nOCT is 1.43, and measured refractive index for THz, nTHz, is 1.53.
| Initial starting values | Difference between algorithm and measured depth (%) | Difference between algorithm and measured refractive index (%) | |||
|---|---|---|---|---|---|
| nOCT initial | nTHz initial | d 1 | d 2 | n OCT | n THz |
| 1.300 | 1.500 | 7.7 | 3.2 | −5.9 | −6.7 |
| 1.300 | 1.600 | 7.7 | 3.2 | −5.9 | −6.7 |
| 1.300 | 1.700 | 7.7 | 3.2 | −5.9 | −6.7 |
| 1.400 | 1.500 | 3.9 | 1.6 | −2.5 | −2.7 |
| 1.400 | 1.600 | 3.9 | 1.6 | −2.5 | −2.7 |
| 1.400 | 1.700 | 3.9 | 1.6 | −2.5 | −2.7 |
| 1.450 | 1.500 | 2.2 | 0.9 | −0.9 | −0.8 |
| 1.450 | 1.550 | 2.2 | 0.9 | −0.9 | −0.8 |
| 1.450 | 1.600 | 2.2 | 0.9 | −0.9 | −0.8 |
| 1.450 | 1.700 | 2.2 | 0.9 | −0.9 | −0.8 |
| 1.500 | 1.400 | 0.5 | 0.2 | 0.8 | 1.0 |
| 1.500 | 1.500 | 0.5 | 0.2 | 0.8 | 1.0 |
| 1.500 | 1.600 | 0.5 | 0.2 | 0.8 | 1.0 |
| 1.500 | 1.700 | 0.5 | 0.2 | 0.8 | 1.0 |
Fig. 4.
Plots showing the convergence of the algorithm over 9 iterations for (a) the THz time-of-flight for region A (circles) and region E (triangles). A full line is plotted at tTHz = 15.665 ps and dotted line at tTHz = 6.647 ps showing the convergence value. (b) The depth determined from each iteration of the algorithm for region A (circles) and region E (triangles) with the full line at d1 = 3.116 mm, and dotted line at d2 = 1.296 mm. (c) The refractive index from the algorithm after each iteration for nTHz (circles) and nOCT (triangles), with a full line at nTHz = 1.517 and nOCT = 1.418 showing convergence.
2.3.5. Calibration and co-registration of the OCT and THz image information
The outcome from the algorithm is a set of four pieces of information: d1 and d2, nOCT, and nTHz. By assuming the medium is uniform prior to the embedded layers, the OCT and THz images can then be scaled according to these refractive index values. These ‘calibrated’ images provide the possibility of overlaying the images by co-registration since they are on equivalent distance scales. To test this, 2D cross-sectional OCT and THz images, known as B-scan images, were co-registered using Matlab’s imregconfig and imregister commands. The ‘multimodal’ option was selected, which maximizes the mutual information between the two images, ignoring the incommensurate intensities of the two modalities, using a one-plus-one evolutionary optimization configuration. Rigid registration was selected since the scale was determined and calibrated by the refractive index. The co-registered OCT and THz B-scan images are shown in Fig. 5 and Fig. 6 together with the photograph of the arrangement and the individual THz and OCT B-scans.
Fig. 5.
(a) Side-view photograph of the test object showing the embedded square silicone-TiO2 test object. THz and OCT were incident on the top surface. (b) B-scan from the OCT image of the test object, showing a scattered signal from the top surface of the test object and increased scatter from the embedded square. (c) B-scan THz image showing reflections from the top surface of the test object, the top surface of the embedded square, and the bottom surface of the test object. (d) The co-registered overlay of the THz and OCT images showing the agreement between the two imaging methods, where the OCT image is in ‘hot’ colourmap for contrast.
Fig. 6.
(a) Side-view photograph of the test object showing the embedded rectangular test object. THz and OCT were incident on the top surface. (b) OCT B-scan image, along the profile shown by the red dotted line in Fig. 1, showing a reflection from the top surface of the test object and increased scatter from the embedded rectangle. (c) B-scan THz image showing reflections from the top surface of the test object, the top surface of the embedded rectangle, and the bottom surface of the test object. (d) The co-registered overlay of the THz and OCT B-scan images showing the agreement between the two imaging methods, where the OCT image is in ‘hot’ colourmap for contrast.
As a further step to test the co-registration of the images, the depth of the embedded rectangle was determined over a profile that was 1 mm wide along the direction shown in Fig. 1(a) by the red dotted line. The depths extracted from the OCT and THz images along this profile were combined to give a depth profile, shown in Fig. 7.
Fig. 7.
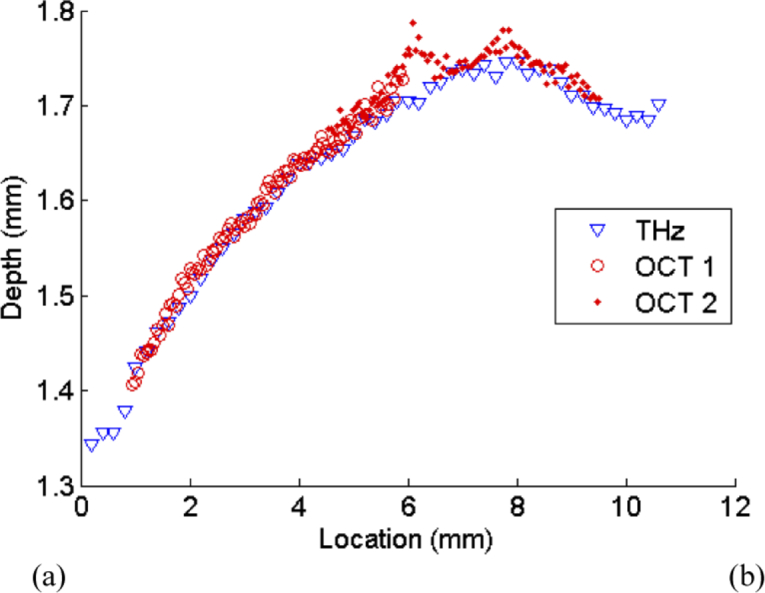
(a) Graph showing the depth of the embedded rectangle along the profile marked in Fig. 1 with a red dotted line. The depth of the layer identified from the THz image is shown as blue triangles, while the depth obtained with OCT images is shown as red circles. ‘OCT 1’ represents the data from the left hand OCT image in Fig. 6(b), while ‘OCT 2’ represents the data from the right hand OCT image
3. Results
The results for the algorithm are presented in Tables 2, 3 and Fig. 4. Table 2 gives the values output by the algorithm for the range of pair locations used in this study compared to the appropriate measured value. Table 3 displays the manner in which the initial starting values for the refractive index of OCT and THz affect the algorithm. Figure 4 demonstrates the convergence of the algorithm over 9 recorded iterations, for the example, pair combination of [A, E], showing how the values converge in under 6 steps.
Figures 5 and 6 show the B-scans for the THz and OCT images of regions in the embedded square and rectangle. The OCT images co-registered by automated image registration are overlaid on the THz images to show the agreement in the two imaging modalities in Fig. 5(d) and Fig. 6(d).
Given the way the phantom was made, the rectangular inclusion was not parallel with the surface. We took advantage of this to determine how accurately the depth of features that were not used to calibrate the algorithm could be determined. The depths were first calibrated using measurements taken from areas A-E as described above, and the results of the algorithm were then applied to the varying depth of the top surface of the rectangle. These depth profiles, taken from the THz and two OCT images are compared in Fig. 7 and show good agreement over depths ranging from 1.3–1.8 mm.
4. Discussion
Overall the algorithm to extract depths and refractive index values using OCT and THz imaging measurements at two unknown depth locations performed well. The mean depth of the silicone test object and depth of the embedded layers calculated from the algorithm agreed within 3.3% of the measured depths. The refractive index values agreed even more closely, within 1.5%. Interestingly the depths from the algorithm were slightly overestimated compared to the measured depth. This corresponded with the refractive index calculated from the algorithm being slightly lower than the measured values.
It might be expected that the wider the depth range, the better the results. However, this was not observed with the analysis. For example, the algorithm gave the same depth for region C when the pair combination of [A, C] and [C, D] were used. The difference in measured depth between regions A and C is 30 µm, while the difference in depth between regions C and D was measured as 1.82 mm. This robustness to the depth of the two locations is promising for the technique to be used with samples that only exhibit a small but detectable variation of depths, for example in skin layers.
The refractive index obtained from the algorithm for OCT was 1.422, which compared favorably to the measured value of 1.43. The difference was just 0.6%. Similarly, for THz frequencies, the mean refractive index obtained from all the pair combinations was 1.507 compared to the value of 1.53 determined from the THz spectroscopy measurements. The difference, in this case, was 1.5%.
The results were almost invariant to the initial nTHz value, as can be seen from Table 2, but did depend on the initial value of nOCT. This may be because nOCT is used in both the determination of the corrected tTHz as well as the solution of the four simultaneous equations. The outcome for depth and refractive index was constant if nTHz varied from 1.5 - 1.7. However, for nOCT ranging from 1.3 - 1.5, the calculated values differed from the measured ones by between 7.7% and 0.2% for the example pair [A, E].
The two examples of co-registration shown in Fig. 5(d) and Fig. 6(d) demonstrates very good visual agreement between the OCT and THz B-scans images. This indicates the scaling of images for the refractive index calculated from the algorithm works well, assuming the medium is uniform, to establish the images on equivalent distance scales that then enables the overlay of the images. This similarity is supported by the fact the images can be co-registered using an automated, unsupervised, rigid registration algorithm, after this scaling.
As a further demonstration of the ability of the algorithm to improve the characterization of the samples, Fig. 7 clearly shows that the profile of the rectangle agrees closely for both the OCT and THz images. This analysis shows that despite even with THz incident on the sample at 30°, by accounting for the known angle of incidence the algorithm still operates successfully.
Using this algorithm, it is possible to combine OCT and THz images to overlay the complementary information they provide. OCT in the past has assumed to be able to extract thickness, with the refractive index assumed from the literature or measured for the material. Potentially this algorithm could be used with OCT alone at two different wavelengths; however, the advantage of combining with THz is that the hydration properties may be obtained that informs the functionality not just structure, and this may be of value to clinicians. Using this algorithm, it may be possible to confirm these thickness measurements. This may be of value, for example, in corneal applications, confirming the thickness of the cornea as well as providing enhanced information from the THz that is sensitive to pathology. This may also advance the combined OCT/THz modality in applications for the skin and breast cancer margin detection, as well as in industry, for non-destructive testing and quality control purposes. The next step to achieving this would be examining how the algorithm operates with multiple layered structures and with layered gradients such as that found in the skin.
5. Conclusion
OCT and THz give different and complementary information that may improve diagnostic and characterization capabilities beyond just using one of the modalities alone. We showed through the use of a silicone test object with TiO2-silicone embedded layers that the THz and OCT images may be used to extract structural information of the object, as well as a refractive index using an iterative algorithm. This method overcomes the challenges of unknown refractive index values and the impact these have on the uncertainty in calculating layer depth.
The algorithm we presented solves four simultaneous equations for four unknowns using OCT and THz measurements at two locations. The outcome of the algorithm is the depth of the two locations as well as the refractive index for the OCT wavelength and THz frequencies. Quantitatively, the thicknesses and depths determined from the image agreed very closely to within 3.3% with the measured values. Refractive index values obtained from the algorithm agreed to within 1.5% of the measured values. The refractive index calculation was more dependent on the initial estimate of the refractive index of OCT wavelengths than THz possibly because of the more significant role this plays in the algorithm.
We presented overlaid THz and OCT images based on these refractive index values that aligned well and showed, for the first time, that THz and OCT images could be automatically scaled and co-registered with unsupervised methods, even without knowing the refractive index in either regime. This allows the complementary information from the OCT structure and THz hydration sensitivity to be overlaid to potentially enhance diagnostic capabilities in applications where the two show promise.
Acknowledgements
We thank Qingyun Li for advising on the operation of OCT, sharing processing code and discussing general OCT questions.
This research was supported by the Australian Government through the Australian Research Council’s Discovery Projects funding scheme (DP1096514, DP150100635). VPW is supported by the Australian Research Council via a Future Fellowship (project number FT180100683) funded by the Australian Government. MH was funded through NHMRC grant 1141552, http://purl.org/au-research/grants/nhmrc/1141552. BC acknowledges funding through the Brain Pool Program from the National Research Foundation of Korea (NRF) funded by the Ministry of Science and ICT (2019H1D3A2A02101784).
Funding
Australian Research Council10.13039/501100000923 (DP1096514, DP150100635, FT180100683); National Health and Medical Research Council10.13039/501100000925 (1141552); National Research Foundation of Korea10.13039/501100003725 funded by the Ministry of Science, ICT and Future Planning10.13039/501100003621Ministry of Science and ICT (2019H1D3A2A02101784).
Disclosures
This work is the subject of an Australian Provisional Patent Application (No. 2019903145).
References
- 1.Huang D., Swanson E. A., Lin C. P., Schuman J. S., Stinson W. G., Chang W., Hee M. R., Flotte T., Gregory K., Puliafito C. A., Fujimoto J. G., “Optical coherence tomography,” Science 254(5035), 1178–1181 (1991). 10.1126/science.1957169 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Grischkowsky D., Keiding S., van Exter M., Fattinger C., “Far-infrared time-domain spectroscopy with terahertz beams of dielectrics and semiconductors,” J. Opt. Soc. Am. B 7(10), 2006–2015 (1990). 10.1364/JOSAB.7.002006 [DOI] [Google Scholar]
- 3.Brezinski M. E., Tearney G. J., Bouma B. E., Izatt J. A., Hee M. R., Swanson E. A., Southern J. F., Fujimoto J. G., “Optical Coherence Tomography for Optical Biopsy,” Circulation 93(6), 1206–1213 (1996). 10.1161/01.CIR.93.6.1206 [DOI] [PubMed] [Google Scholar]
- 4.Pan Y., Birngruber R., Engelhardt R., “Contrast limits of coherence-gated imaging in scattering media,” Appl. Opt. 36(13), 2979–2983 (1997). 10.1364/AO.36.002979 [DOI] [PubMed] [Google Scholar]
- 5.Kindt J. T., Schmuttenmaer C. A., “Far-Infrared Dielectric Properties of Polar Liquids Probed by Femtosecond Terahertz Pulse Spectroscopy,” J. Phys. Chem. 100(24), 10373–10379 (1996). 10.1021/jp960141g [DOI] [Google Scholar]
- 6.Pickwell E., Wallace V. P., “Biomedical applications of terahertz technology,” J. Phys. D: Appl. Phys. 39(17), R301–R310 (2006). 10.1088/0022-3727/39/17/R01 [DOI] [Google Scholar]
- 7.Heyden M., Ebbinghaus S., Havenith M, “Terahertz Spectroscopy as a Tool to Study Hydration Dynamics,” in Encyclopedia of Analytical Chemistry, Meyers R. A., ed. (Wiley, 2010). [Google Scholar]
- 8.Taylor Z. D., Singh R. S., Bennett D. B., Tewari P., Kealey C. P., Bajwa N., Culjat M. O., Stojadinovic A., Lee H., Hubschman J., Brown E. R., Grundfest W. S., “THz Medical Imaging: in vivo Hydration Sensing,” IEEE Trans. Terahertz Sci. Technol. 1(1), 201–219 (2011). 10.1109/TTHZ.2011.2159551 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Sun Q., Parrott E. P. J., He Y., Pickwell-MacPherson E., “In vivo THz imaging of human skin: Accounting for occlusion effects,” J. Biophotonics 11(2), e201700111 (2018). 10.1002/jbio.201700111 [DOI] [PubMed] [Google Scholar]
- 10.Berry E., Handley J. W., Fitzgerald A. J., Merchant W. J., Boyle R. D., Zinov’ev N. N., Miles R. E., Chamberlain J. M., Smith M. A., “Multispectral classification techniques for terahertz pulsed imaging: an example in histopathology,” Med. Eng. Phys. 26(5), 423–430 (2004). 10.1016/j.medengphy.2004.02.011 [DOI] [PubMed] [Google Scholar]
- 11.Fitzgerald A. J., Wallace V. P., Pinder S. E., Purushotham A. D., O’Kelly P., Ashworth P. C., “Classification of terahertz-pulsed imaging data from excised breast tissue,” J. Biomed. Opt. 17(1), 016005 (2012). 10.1117/1.JBO.17.1.016005 [DOI] [PubMed] [Google Scholar]
- 12.Fitzgerald A. J., Wallace V. P., Jimenez-Linan M., Bobrow L., Pye R. J., Purushotham A. D., Arnone D. D., “Terahertz Pulsed Imaging of Human Breast Tumors,” Radiology 239(2), 533–540 (2006). 10.1148/radiol.2392041315 [DOI] [PubMed] [Google Scholar]
- 13.Woodward R. M., Cole B. E., Wallace V. P., Pye R. J., Arnone D. D., Linfield E. H., Pepper M., “Terahertz pulse imaging in reflection geometry of human skin cancer and skin tissue,” Phys. Med. Biol. 47(21), 3853–3863 (2002). 10.1088/0031-9155/47/21/325 [DOI] [PubMed] [Google Scholar]
- 14.Chernomyrdin N. V., Dolganova I., Beshplav S.-I., Komandin G., Reshetov I. V., Potapov A. A., Tuchin V., Zaytsev K., Alexandrova P. V., Malakhov K., Nikitin P. V., Kosyr’kova A. V., Musina G., Differentiation of healthy and malignant brain tissues using terahertz pulsed spectroscopy and optical coherence tomography (2019), p. 5.
- 15.Vakoc B. J., Fukumura D., Jain R. K., Bouma B. E., “Cancer imaging by optical coherence tomography: preclinical progress and clinical potential,” Nat. Rev. Cancer 12(5), 363–368 (2012). 10.1038/nrc3235 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Wang J., Sun Q., Stantchev R. I., Chiu T.-W., Ahuja A. T., Pickwell-MacPherson E., “In vivo terahertz imaging to evaluate scar treatment strategies: silicone gel sheeting,” Biomed. Opt. Express 10(7), 3584–3590 (2019). 10.1364/BOE.10.003584 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Crowther J. M., Sieg A., Blenkiron P., Marcott C., Matts P. J., Kaczvinsky J. R., Rawlings A. V., “Measuring the effects of topical moisturizers on changes in stratum corneum thickness, water gradients and hydration in vivo,” Br. J. Dermatol. 159, 567–577 (2008). 10.1111/j.1365-2133.2008.08703.x [DOI] [PubMed] [Google Scholar]
- 18.Bennett D. B., Taylor Z. D., Tewari P., Singh R. S., Culjat M. O., Grundfest W. S., Sassoon D. J., Johnson R. D., Hubschman J.-P., Brown E. R., “Terahertz sensing in corneal tissues,” J. Biomed. Opt. 16(5), 057003 (2011). 10.1117/1.3575168 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Pircher M., Götzinger E., Leitgeb R., Fercher A. F., Hitzenberger C. K., “Measurement and imaging of water concentration in human cornea with differential absorption optical coherence tomography,” Opt. Express 11(18), 2190–2197 (2003). 10.1364/OE.11.002190 [DOI] [PubMed] [Google Scholar]
- 20.Fitzgerald A. J., Cole B. E., Taday P. F., “Nondestructive analysis of tablet coating thicknesses using terahertz pulsed imaging,” J. Pharm. Sci. 94(1), 177–183 (2005). 10.1002/jps.20225 [DOI] [PubMed] [Google Scholar]
- 21.Lin H., Dong Y., Markl D., Williams B. M., Zheng Y., Shen Y., Zeitler J. A., “Measurement of the Intertablet Coating Uniformity of a Pharmaceutical Pan Coating Process With Combined Terahertz and Optical Coherence Tomography In-Line Sensing,” J. Pharm. Sci. 106(4), 1075–1084 (2017). 10.1016/j.xphs.2016.12.012 [DOI] [PubMed] [Google Scholar]
- 22.Adam A. J. L., Planken P. C. M., Meloni S., Dik J., “TeraHertz imaging of hidden paint layers on canvas,” Opt. Express 17(5), 3407–3416 (2009). 10.1364/OE.17.003407 [DOI] [PubMed] [Google Scholar]
- 23.Seco-Martorell C., Lopez-Dominguez V., Arauz-Garofalo G., Redo-Sanchez A., Palacios J., Tejada J., Goya’s artwork imaging with Terahertz waves (2013), Vol. 21, pp. 17800–17805. [DOI] [PubMed] [Google Scholar]
- 24.Cheung C. S., Spring M., Liang H., “Ultra-high resolution Fourier domain optical coherence tomography for old master paintings,” Opt. Express 23(8), 10145–10157 (2015). 10.1364/OE.23.010145 [DOI] [PubMed] [Google Scholar]
- 25.Iwanicka M., Kwiatkowska E. A., Sylwestrzak M., Targowski P., Application of optical coherence tomography (OCT) for real time monitoring of consolidation of the paint layer in Hinterglasmalerei objects, SPIE Optical Metrology (SPIE, 2011), Vol. 8084. [Google Scholar]
- 26.Targowski P., Rouba B., Góra M., Tymińska-Widmer L., Marczak J., Kowalczyk A., “Optical coherence tomography in art diagnostics and restoration,” Appl. Phys. A 92(1), 1–9 (2008). 10.1007/s00339-008-4446-x [DOI] [Google Scholar]
- 27.Gibson A., Piquette K. E., Bergmann U., Christens-Barry W., Davis G., Endrizzi M., Fan S., Farsiu S., Fitzgerald A., Griffiths J., Jones C., Li G., Manning P. L., Maughan Jones C., Mazza R., Mills D., Modregger P., Munro P. R. T., Olivo A., Stevenson A., Venugopal B., Wallace V., Wogelius R. A., Toth M. B., Terras M., “An assessment of multimodal imaging of subsurface text in mummy cartonnage using surrogate papyrus phantoms,” Heritage Sci. 6(1), 7 (2018). 10.1186/s40494-018-0175-4 [DOI] [Google Scholar]
- 28.Eghrari A. O., Gottsch J. D., “Fuchs’ corneal dystrophy,” Expert Rev. Ophthalmol. 5(2), 147–159 (2010). 10.1586/eop.10.8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Güell J. L., El Husseiny M. A., Manero F., Gris O., Elies D., “Historical Review and Update of Surgical Treatment for Corneal Endothelial Diseases,” Ophthalmol. Ther. 3(1-2), 1–15 (2014). 10.1007/s40123-014-0022-y [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Woodward R. M., Wallace V. P., Pye R. J., Cole B. E., Arnone D. D., Linfield E. H., Pepper M., “Terahertz pulse imaging of ex vivo basal cell carcinoma,” J. Invest. Dermatol. 120(1), 72–78 (2003). 10.1046/j.1523-1747.2003.12013.x [DOI] [PubMed] [Google Scholar]
- 31.Taylor Z. D., Garritano J., Sung S., Bajwa N., Bennett D. B., Nowroozi B., Tewari P., Sayre J. W., Hubschman J. P., Deng S. X., Brown E. R., Grundfest W. S., “THz and mm-Wave Sensing of Corneal Tissue Water Content: In Vivo Sensing and Imaging Results,” IEEE Trans. Terahertz Sci. Technol. 5(2), 184–196 (2015). 10.1109/TTHZ.2015.2392628 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Lamouche G., Kennedy B. F., Kennedy K. M., Bisaillon C.-E., Curatolo A., Campbell G., Pazos V., Sampson D. D., “Review of tissue simulating phantoms with controllable optical, mechanical and structural properties for use in optical coherence tomography,” Biomed. Opt. Express 3(6), 1381–1398 (2012). 10.1364/BOE.3.001381 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Bruin D. M. M. D., Bremmer R. H., Kodach V. M., Kinkelder R. D., Marle J. V., Leeuwen T. G. V., Faber D. J., “Optical phantoms of varying geometry based on thin building blocks with controlled optical properties,” J. Biomed. Opt. 15(01), 1–10 (2010). 10.1117/1.3277668 [DOI] [PubMed] [Google Scholar]
- 34.Kennedy B. F., Hillman T. R., McLaughlin R. A., Quirk B. C., Sampson D. D., “In vivo dynamic optical coherence elastography using a ring actuator,” Opt. Express 17(24), 21762–21772 (2009). 10.1364/OE.17.021762 [DOI] [PubMed] [Google Scholar]
- 35.Curatolo A., Kennedy B. F., Sampson D. D., “Structured three-dimensional optical phantom for optical coherence tomography,” Opt. Express 19(20), 19480–19485 (2011). 10.1364/OE.19.019480 [DOI] [PubMed] [Google Scholar]
- 36.Brunner F. D. J., Schneider A., Günter P., “A terahertz time-domain spectrometer for simultaneous transmission and reflection measurements at normal incidence,” Opt. Express 17(23), 20684–20693 (2009). 10.1364/OE.17.020684 [DOI] [PubMed] [Google Scholar]
- 37.Cassar Q., Al-Ibadi A., Mavarani L., Hillger P., Grzyb J., MacGrogan G., Zimmer T., Pfeiffer U. R., Guillet J.-P., Mounaix P., “Pilot study of freshly excised breast tissue response in the 300–600 GHz range,” Biomed. Opt. Express 9(7), 2930–2942 (2018). 10.1364/BOE.9.002930 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Li Q., Karnowski K., Noble P. B., Cairncross A., James A., Villiger M., Sampson D. D., “Robust reconstruction of local optic axis orientation with fiber-based polarization-sensitive optical coherence tomography,” Biomed. Opt. Express 9(11), 5437–5455 (2018). 10.1364/BOE.9.005437 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Walther J., Li Q., Villiger M., Farah C. S., Koch E., Karnowski K., Sampson D. D., “Depth-resolved birefringence imaging of collagen fiber organization in the human oral mucosa in vivo,” Biomed. Opt. Express 10(4), 1942–1956 (2019). 10.1364/BOE.10.001942 [DOI] [PMC free article] [PubMed] [Google Scholar]