Revisiting van der Waals Radii: From Comprehensive Structural Analysis to Knowledge‐Based Classification of Interatomic Contacts

Abstract

Weak noncovalent interactions are responsible for structure and properties of almost all supramolecular systems, such as nucleic acids, enzymes, and pharmaceutical crystals. However, the analysis of their significance and structural role is not straightforward and commonly requires model studies. Herein, we describe an efficient and universal approach for the analysis of noncovalent interactions and determination of van der Waals radii using the line‐of‐sight (LoS) concept. The LoS allows to unambiguously identify and classify the “direct” interatomic contacts in complex molecular systems. This approach not only provides an improved theoretical base to molecular “sizes” but also enables the quantitative analysis of specificity, anisotropy, and steric effects of intermolecular interactions.

Seeing trees behind the forest! A method based on the line‐of‐sight concept to efficiently eliminate the background from randomly distributed contacts and analyze intermolecular interactions within diverse extended structural datasets is presented. This approach allowed to more specifically define the vdW parameters from the bulk structural data and to identify atom‐type specific vdW radii with clear physical meaning.

1. Introduction

Van der Waals (vdW) radii (R _vdW) are one of the cornerstones of contemporary chemistry. The visual perception and basic analysis of chemical structures and architectures are strongly related to the concept of vdW radii, which provides the basic definition of the atomic “sizes”. Even though this concept has little physical grounding, it is easily interpretable and therefore widely used in the theoretical chemistry, particularly in design of force fields (in the Lennard‐Jones parameter form),1 dispersion corrections,2 and COSMO‐RS‐type solvate models.3 These models operate – directly or indirectly – by the intermolecular interatomic distances, which are regarded as corresponding to the minimum energy of atom‐atom interactions, and are usually defined as a function of the sum of vdW radii. However, it has been noted4, 5 that the sum of R _vdW for available vdW sets including the most widely used one tabulated by Bondi6 consistently underestimate the position of the energy minimum by as much as 0.3–0.4 Å. An illustrative example is a C₂Cl₆ crystal with the shortest r(Cl ⋅⋅⋅ Cl)=3.65 Å that exceeds significantly the 2R _vdW ^B°^ndi (Cl)=3.50 Å. The latter can only be achieved at a very high pressure of ca. 1.2 GPa.7 Moreover, about 2.0 % (>4000) of unique organic molecular crystals in the Cambridge Structural Database (CSD)8 do not contain intermolecular contacts shorter than the sum of R _vdW ^B°^ndi (see the first section of Supporting Information for details). The question arises: why are all bonds in these crystals longer than the distance, which is usually considered as the most probable, in other words, closest to the energy minimum of the respective interatomic potential?

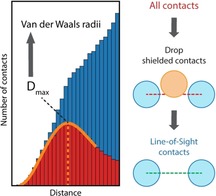
This inconsistency is rooted in the indirect nature of the approaches used to obtain the vdW parameters from experimental structural datasets. Conventionally, R _vdW are derived from the position of the vdW peak in the distributions of contact distances between nonbonded atoms (Figure 1a,b).6, 9, 10 Such distributions represent a superposition of a gaussian curve due to the vdW peak, and a rapidly growing function due to the randomly distributed contacts (Figure 1a). Because the position of the vdW peak maximum (D _max) is often hidden within the dataset for other contacts (Figure 1b), the sum of vdW radii is normally taken as the half‐height of the vdW peak distance, D _half instead of the D _max (Figure 1a). However, D _max has a clearer physical meaning as corresponding to the most probable distance for the considered interaction.4 On the contrary, D _half‐based vdW radii are qualitative, as the interpretation of their sum is not straightforward. It should be mentioned here that the relation between statistical distributions and energy surfaces is not straightforward and cannot be quantitatively determined without introducing arbitrary and unwarranted assumptions.11 However, low‐energy regions of molecular potential energy surfaces can be recognized and mapped from distributions of observed structures, thus D _max can be considered an approximation of the “minimum energy position”.4, 11

Figure 1.

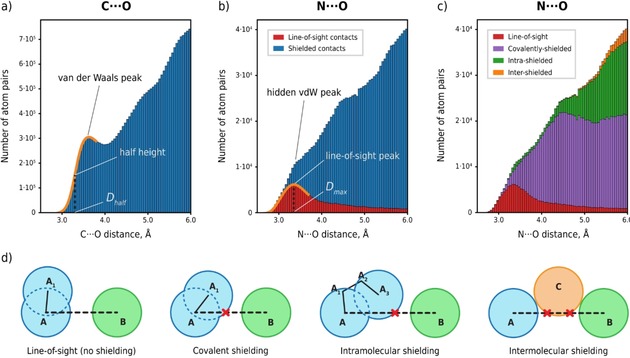
Distance distributions for all C ⋅⋅⋅ O (a) and N ⋅⋅⋅ O (b,c) intermolecular contacts from molecular crystals in CSD. The contacts between atom pairs are classified as the line‐of‐sight and various shielded contacts (d). The respective contributions to the overall contact distance distributions of r(N ⋅⋅⋅ O) are presented in parts (b,c).

Although alternative knowledge‐based12 approaches to derive R_vdW were proposed, similar to the original Bondi's strategy they fail to extract the most probable interatomic distances from the structural data. In addition to statistical approaches, several ab initio computational ways to derive atomic sizes and R_vdW have been proposed.13, 14 However, the real systems are much more complex than the computational models. As a result, such computational approaches provide only qualitative radii values and their use for the analysis of real extended systems therefore necessitates further investigations to ensure an adequate connection with the experimental results.

In this work, we introduce a new method to define the D_max and, accordingly, to compute D _max‐based vdW radii (R _max) for almost any intermolecular interaction directly from diverse structural datasets. The key idea is to eliminate the background from randomly distributed contacts using the Line‐of‐Sight15 concept. It considers a pair of atoms as interacting only when they “see” each other (Figure 1d) because no other atom in the structure intrudes between them or, in other words, shields them from one other. This concept allows one to redetermine vdW parameters from the bulk structural data and provide an opportunity to find atom‐type specific D _max‐based vdW radii for elements in different chemical environments with clear physical meaning. It should be noted that intermolecular interactions cannot be reduced to atom‐atom interactions16 and energy decomposition schemes should rather be applied for a detailed analysis.17 Nevertheless, our approach is in fact a statistical way to localize the most probable geometries of intermolecular interactions, which is independent of the interpretation of the results in terms of atom‐atom interactions. We argue that R _max can be used to improve the accuracy of computational approaches directly or indirectly involving consideration of the size of molecules. It will be useful for the analysis of intermolecular interactions in combination with quantum chemistry methods.

2. Results and Discussion

We propose to implement the Line‐of‐Sight15 concept (LoS) to eliminate the background from randomly distributed contacts, which is equivalent to classification of contacts into corresponding and noncorresponding to interatomic interactions. Thus, we start with understanding the physical meaning of this procedure. LoS concept considers the atoms as interacting only when they “see” each other (Figure 1d) because no other atom in the structure intrudes between them or, in other words, shields them from one another (for the exact definition see the SI). We identify three main types of contact shielding, namely, the covalent, intra‐ and intermolecular shielding depending on the type of shielding atom (Figure 1d), with only the covalent shielding having the characteristic distances comparable to those of the D _max. A representative example of the contributions from the LoS and shielded contacts for the complete dataset of N ⋅⋅⋅ O contacts is illustrated in Figure 1c.

To qualitatively validate and illustrate this concept, we carried out a detailed conformational and bonding analysis on a model H₃N ⋅⋅⋅ CH₃F system (Figure 2) by means of density functional theory (DFT) calculations (B3LYP/6‐311++G(d,p)). The ab initio electron density‐based noncovalent interaction surface (NCIS) method18 was employed to detect and estimate the intermolecular interactions. Basic geometric considerations within the LoS model imply the N ⋅⋅⋅ C interaction for a configuration with ∠N ⋅⋅⋅ C−F of 180° and ∠N ⋅⋅⋅ C−H of ∼70°. The decrease of ∠N ⋅⋅⋅ C−F would result in the gradual shielding of the N ⋅⋅⋅ C contact by the H atoms and ultimately vanishing the N ⋅⋅⋅ C interaction at ∠N ⋅⋅⋅ C−F∼155–160° and ∠N ⋅⋅⋅ C−H∼45–50°, depending on the assumed R _vdW. The NCIS analysis supports these predictions (Figure 2). The NCIS has a pronounced maximum between the N and C atoms in linear H₃N ⋅⋅⋅ CH₃F. Upon bending the geometry, the NCIS redistributes towards the N ⋅⋅⋅ H area evidencing strengthening of the respective N ⋅⋅⋅ H contact with a concomitant weakening of the initial N ⋅⋅⋅ C interaction (Figure 2). These data show that the shielding does not fully eliminate the original two‐atom contact but rather decreases its contribution to the overall intermolecular interaction. On contrary, the LoS contacts are dominated by their respective diatomic contributions that makes them perfectly suitable for the statistical analysis of the intermolecular contacts. Note that strictly speaking the LoS approach cannot be used as a criterion of significance of intermolecular interactions. The presented results and analysis are not sufficient to unambiguously evaluate whether only LoS contacts give rise to significant intermolecular interactions.

Figure 2.

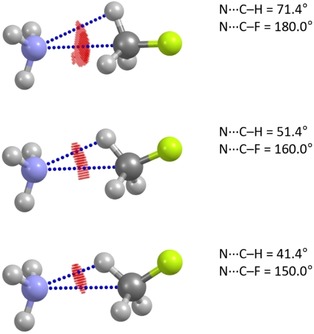
Dependence of NCI surface (isosurface value is set to 0.5) in the H₃N ⋅⋅⋅ H₃CF system on N ⋅⋅⋅ C−F angle and N ⋅⋅⋅  (H)C shielding.

The LoS concept was next used to determine the vdW radii for the main group elements from the structural data in the Cambridge Structural Database (CSD).8 We processed 224 001 unique CSD entries, from which more than 40 000 000 intermolecular LoS contacts were obtained and analyzed. An iterative procedure was employed, in which at the 0^th iteration, the LoS was defined with Bondi's R _vdW.6 The LoS contact distance distributions were used to determine D _max values for all possible A ⋅⋅⋅ B atom pair contacts, while the D _max values were used to compute the vdW radii, R _vdW, for all elements in the dataset by means of least‐squares minimization of the function [Eq. (1)]:

$${\displaystyle f=\Sigma {}_{\mathrm{A}···\mathrm{B}}w(\mathrm{A}···\mathrm{B})·[D{}_{\max }(\mathrm{A}···\mathrm{B})-R{}_{\mathrm{vdW}}\left(\mathrm{A}\right)-R{}_{\mathrm{vdW}}\left(\mathrm{B}\right)]{}^2}$$ (1)

where the outer summation is carried out over all selected A ⋅⋅⋅ B contacts, and w(A ⋅⋅⋅ B) is a weight defined as the root square of the number of LoS contacts shorter than D _max. This weight function was chosen to eliminate bias caused by the determination of D _max values of distributions based on a small number of contacts from the vdW radii. However, the use of the degenerate weight function (w(A ⋅⋅⋅ B)=1) gives almost the same R _vdW values with the largest deviation of 0.02 Å. Because the contact shielding depends on vdW radii, the R _vdW values obtained at the first step were used to recalculate the contact shielding parameters and determine the D _max values for all atom pairs. This procedure was repeated iteratively until convergence of 0.001 Å was reached for all R _vdW.

For some atom pairs, it was not possible to accurately locate D _max due to the imperfect shape of the gaussian peak in the LoS distribution. This can be attributed to one of the following three scenarios, namely, (1) a small total number of contacts, (2) the analyzed contact type consists of several contact subtypes characterized by different D _max values, resulting in a significant broadening of the vdW peak, and (3) significant dependence of the D _max on the contact geometry, which also widens the vdW peak. Addressing the second scenario by splitting the contact type into subtypes reduces the number of contacts and therefore often gives rise to the first scenario. As a result, we were able to obtain D _max for type‐specific contacts with C (C_sp2 and C_sp3) and O (O_sp2 and O_sp3) atoms only. On the contrary, for B, P, and As we were not able to accurately obtain D _max for any contact type. It should be noted that for N, S, and Se, which have several common atom types, we were able to identify one atom type, namely, the N_sp3, S_sp3 and Se_sp3, as other types of these elements exhibit a significant dependence on contact geometry (the second scenario).

Applying the R _vdW search procedure to the selected contact types has revealed that for some contacts D _max significantly deviates from the sum of the atomic type‐specific R _vdW (Table S1). Such deviations are observed either when the contact corresponds to a potentially specific interaction (e. g. hydrogen or halogen bond) or the interacting atoms are possibly sterically hindered. Such contacts were not used to determine R _vdW as our final goal was to obtain R _vdW corresponding to weak nonspecific interactions that were not affected by secondary effects. The contacts used for R _vdW determination are marked with ‘+’ sign in the second column of Table S1. The R _vdW values determined using this procedure (R_max) are listed in Table 1 and compared with the respective values from the most popular vdW radii sets (R _half).

Table 1.

Van der Waals radii of elements typical for organic compounds.

Atom	Van der Waals radii [Å]					Atom or contact type[a]
	R half			R QM 14	R max
	Bondi6	R.&T.9	Alv.10
H	–	–	–	1.54	1.21	C−H ⋅⋅⋅ X, X≠H
	1.20	–	1.20		1.29	C−H ⋅⋅⋅ H−C
C	1.70	1.75	1.77	1.90	1.87	Csp2
	–	–	–		1.91	Csp3, (C−Me)
N	1.55	1.61	1.66	1.79	1.76	Nsp3 ([R/H]3N)
O	1.52	1.56	1.50	1.71	1.74	Osp3 (ROH/R2O)[b]
	–	–	–		1.65	Osp2 (C=O)[c]
F	1.47	1.44	1.46	1.63	1.55	C−F
S	1.80	1.79	1.89	2.14	1.95	R2S
Cl	1.75	1.74	1.82	2.06	1.91	C−Cl
Se	1.90	–	1.82	2.24	2.04	Z2Se
Br	1.85	1.85	1.86	2.19	2.00	C−Br
I	1.98	2.00	2.04	2.38	2.17	C−I

[a] Atom types used for determination of van der Waals radii in this work. If there are several radii for one element, the first row lists “default” R_vdW for the current element that can be compared with the values from other vdW radii sets. R and Z in formulae stands for C‐bonded and any monovalent substituents, respectively. [b] Water molecules were excluded as D _max of the respective interactions were systematically different from those for ROH/R₂O. [c] Carboxylates and charged atoms were excluded from the datasets as the D _max of the corresponding interactions were systematically different from those for uncharged atoms, which is apparently due to the increased electrostatic contribution.

The results in Table 1 reveals that the LoS model yields vdW radii consistently exceeding the values obtained by D _half‐based approaches by as much as 0.10–0.20 Å resulting in the increase of the sum of R _vdW by 0.2–0.4 Å. This is attributed to the transition of the analysis from the rather arbitrary D _half parameters to more specific and rigorously defined D _max values. We argue that R _max are more physically sound as they directly reflect the most probable contact distance, whereas R _half appear to correspond to strongly shortened interactions, which are usually denoted as “specific” in the chemical literature.

Interestingly, the vdW radii estimates from quantum chemical calculations for isolated atoms (R _QM) by Rahm et al.,14 defined as the average distance from the nucleus to a point where the electron density falls to 0.001 a.u., also exceed R _half (Table 1). The comparison with the data obtained in this work shows that these theoretical R_QM values cohere well with R _max for C, N, O, and F, whereas they quite uniformly exceed R _max for S, Se, Cl, Br and I by 0.15–0.20 Å. This implies that the electron density parameters for weak interactions at the most probable distance depend only weakly on the interacting elements.

Furthermore, our data analysis allows identifying the contact‐angle dependencies in vdW radii. A representative example is the interhalogen interactions C−Hal₁ ⋅⋅⋅ Hal₂−C, Hal=Cl, Br, I (X‐bonds, XBs), which are usually classified as types I and II.19 Type I XBs are characterized by ∠C−Hal₁ ⋅⋅⋅ Hal₂≈∠C−Hal₂ ⋅⋅⋅ Hal₁ and are usually nonspecific and weak, whereas type II XBs are characterized by ∠C−Hal₁ ⋅⋅⋅ Hal₂≈90° and ∠C−Hal₂ ⋅⋅⋅ Hal₁≈180° and are usually strong and shorter than type I XBs due to the σ‐hole interaction.20 Therefore, our approach can specifically be used to discriminate the respective noncovalent interactions and obtain different R _max(Hal) values for 90° and 180° C−Hal ⋅⋅⋅ X angles (see for examples Figures S3–27–29, 49–51, 64–66, 73–75). It should also be noted, that different R _max values were obtained for H atoms from H ⋅⋅⋅ H and H ⋅⋅⋅ X, X≠H contacts (1.21 Å and 1.29 Å, respectively). This should be considered when analyzing interactions between aliphatic tails.

It should be noted, that R _max are in fact a condensed representation of the analyzed contacts and therefore can be instrumental for the more detailed analysis of noncovalent interactions and statistical definition of qualitative structural features of chemical systems. For example, specific interactions and sterically hindered contacts can be automatically identified by D _max substantially deviating from the sum of the respective vdW radii. Let us consider two representative examples of CH ⋅⋅⋅ O and C ⋅⋅⋅ O contacts, for which the D _max are, respectively, shorter or longer than the sum of R _max.

CH ⋅⋅⋅ O contacts show D _max values shorter by 0.14 Å than the sum of R _max. This deviation is much larger than that (<0.02 Å) detected for the related CH ⋅⋅⋅ N and CH ⋅⋅⋅ F interactions (Table S1). The CH ⋅⋅⋅ O contacts are shorter by 0.18 Å than CH ⋅⋅⋅ N and very similar to CH ⋅⋅⋅ F (Figure 3a), although an opposite trend can be seen in the C_sp2 ⋅⋅⋅ O/N/F contacts (Figure 3b). Such deviation of D _max from the sum of R _max implies that CH ⋅⋅⋅ O contacts are highly specific and their structure‐forming role is more significant than that of the other CH ⋅⋅⋅ X contacts, including CH ⋅⋅⋅ F, despite the similar electrostatic nature of these contact types.22

Figure 3.

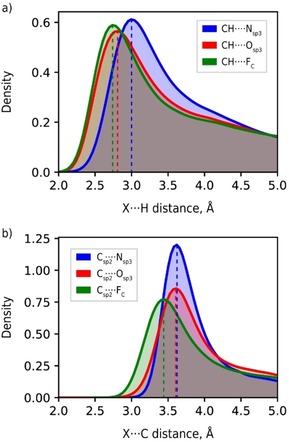
Distance distribution of C−H ⋅⋅⋅ X (a) and C_sp2 ⋅⋅⋅ X (b) line‐of‐sight contacts for X=N, O, F. Gaussian kernel density estimation21 is used instead of histograms for the purpose of clarity.

The C_CR4 ⋅⋅⋅ O contacts formed by quaternary carbon exceed by 0.30 Å the corresponding R _max sum, which, in turn, cohere well with the D _max values for the C ⋅⋅⋅ O contacts formed by primary (C_Me) and tertiary (C_HR3) carbon atoms (Figure 4). Such a shift of the C_CR4 ⋅⋅⋅ O vdW peak is in line with the expected significant steric repulsions between the neighbors of the interacting carbon atom and the oxygen atom and indicates significant steric hinderance of C_CR4 atoms. This means that the concept of vdW radii should be applied with a special care when dealing with the atoms in confined tetrahedral or octahedral environments (e. g. Si, Bi, most of d, f‐elements, and other elements considered by Alvarez in Ref. [10]), which would show an increased effective size due to the unaccounted steric effects. The corresponding D _max values will merely indicate the position of the first maximum of the radial distribution function and make little sense in terms of noncovalent interactions. Only the atoms in an “open” environment such as trigonal, square planar or square pyramidal configurations can be used to determine R _vdW from contact distance distributions without shielding effects to be crucial. Even for the extended dataset considered herein these conditions were fully satisfied only for the 10 elements, which data are summarized in Table 1.

Figure 4.

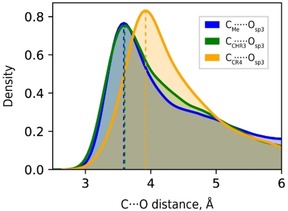
Distance distribution of C ⋅⋅⋅ O_sp3 line‐of‐sight contacts for different carbon types. Gaussian kernel density estimations used instead of histograms for the purpose of clarity.

These examples illustrate that despite all advantages, the element‐defined R _max radii still fail to generally define the most probable distances of intermolecular interactions. The preferred and more accurate approach is to directly utilize D _max values determined for the given atom pair contact rather than the sum of vdW radii. In this way, the structural analysis will automatically account for the specificity of the analyzed interactions, their anisotropy, and the impact of steric effects. We have developed an algorithm and implemented it in a script (deposited at the GitHub23) that allows searching the CSD for intermolecular contacts with certain geometry (ConQuest output) with their subsequent classification as line‐of‐sight or shielded contacts (Figure 5). The produced datasets can readily be used for the determination of the D _max using any standard table processing or data analysis software. Such D _max values obtained for specific contacts with a certain geometry can be used to create high‐throughput geometry‐based descriptors of intermolecular interactions, applicable e. g. to high‐throughput screening of heterogeneous catalysts.24

Figure 5.

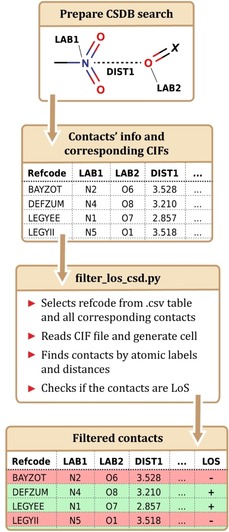
Description of developed workflow for non‐LoS contacts filtration.

Although the described approach is statistical, it can be used for the analysis of specific systems. In this case, one needs to compare the length of an intermolecular contact with D _max of the distribution of the corresponding contacts. Detailization of the environment of interacting atoms and interaction geometry eliminates the bias caused by differences in the nature of atoms and anisotropy of the interaction. As a result, one can localize the most probable geometry of the specific condensed system using experimental structural data. The same outcome can be achieved by analyzing potential energy surface by means of quantum chemical modeling, however, its application to condensed systems is qualitative and not straightforward.25

As a representative example of the approach we provide the analysis of the short F ⋅⋅⋅ F contact in crystalline pentafluorobenzoic acid (PFBA, CSD refcode PFBZAC01).26 It is 2.63 Å long, and both C−F ⋅⋅⋅ F are equal to 155°. This is much shorter than the sum of the element‐specific R _max (3.10 Å) suggesting that such a contact should be forced and potentially repulsive in nature. However, this conclusion does not hold when atom‐type specific radii are utilized for the analysis. The interatomic contact cannot anymore be regarded as an ultrashort one when considering D _max for linear F ⋅⋅⋅ F contacts (2.90 Å), or, even more specifically, the aromatic C₃F₃ fragments (2.78 Å). (Figure 6). Unfortunately, further refinement of the fluorine‐containing fragments is currently not possible due to the small amount of available structural data. However, given that the fluorine environment in PFBA is more electronegative than in more common C₆F₅ groups, we can assume that the most probable r(F ⋅⋅⋅ F) in PFBA is even smaller than 2.78 Å. This implies that such “ultrashort” contact is the intrinsic characteristics of the molecule itself and the role of the packing features for their occurrence is only minor if any.

Figure 6.

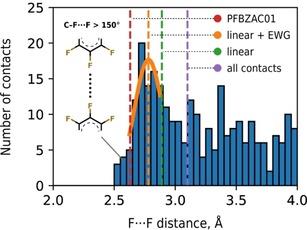
Distance distribution for linear (C−F ⋅⋅⋅ F>150°) intermolecular F ⋅⋅⋅ F contacts between two electron‐withdrawing (EWG) fragments. From left to right: red dashed line denotes the shortest F ⋅⋅⋅ F intermolecular distance in PFBZAC01; orange line stands for D _max of linear F ⋅⋅⋅ F contacts between two aromatic fragments; green and purple lines stand for D _max of linear and all F ⋅⋅⋅ F contacts, respectively.

3. Conclusions

In summary, a new approach for automated analysis and classification of noncovalent interactions has been developed. The key feature of the reported methodology is the filtration of the direct interatomic contacts from the other background structural features based on the LoS concept. The validity of this approach has been confirmed by density functional theory calculations. The LoS concept was used to recompute R _vdW for light elements, which turned out to be substantially larger than those currently accepted by the chemistry community. Our analysis reveals that the underestimations of the “atomic sizes” noted earlier for most tabulated vdW radii (R _half) is solely related to the deficiencies of the datasets used for their determination. The R _max introduced here are free from statistical bias and are based on clear physical grounds. We anticipate the high practical utility of R _max, and particularly, their atom type‐specific variations for improving of molecular sizes in different chemical methods and approaches, and for the analysis of intermolecular interactions on a wide variety of systems including the experimental structural databases and the results of theoretical calculations on molecular and condensed systems relevant to various fields of chemistry and material sciences. The current LoS approach implemented now in the relevant software enables the quantitative analysis of specificity, anisotropy and steric effects of intermolecular interactions while benchmarking databases as well as studying specific systems.

Computational Methods

Version 5.39 with 4 updates (up to August 2018) of CSD8 was used for selection of organic crystals containing H(D), B, C, N, O, F, Si, P, S, Cl, As, Se, Br and I atoms. Disordered, erroneous, polymeric, pressurized, powder structures and experiments with R‐factor >0.075 were removed from consideration. 224 001 selected crystals were used for search of unique intermolecular contacts A ⋅⋅⋅ B with distance D(A ⋅⋅⋅ B) up to 7.0 Å. C−H, N−H and O−H bond lengths were normalized to CCDC/ConQuest defaults: C−H: 1.089 Å, N−H: 1.015 Å, O−H: 0.993 Å. Acetylenic C_sp−H bond lengths were normalized to 1.06 Å (neutron diffraction: ACETYL05, RALDEN01, XEHLEB, ZULDEP01), and S−H bond lengths were normalized to 1.34 Å (microwave data: H₂S,27 neutron diffraction: NALCYS02). For each contact the following information were collected: (1) contact geometry, (2) chemical nature of contact atoms, (3) shielding atom, and (4) contact shielding value. A total of c.a. 640 000 000 contacts were found, more than 40 000 000 of which was LoS depending on used vdW radii (41 346 551 for the final version from Table 1). These data were used further to build and analyze the distribution of distances of various contacts and is available for download.28

Obtained line‐of‐sight A ⋅⋅⋅ B contacts were used to plot histograms of contact distance distributions for all possible A, B atom type pairs (Table S1). Primary analysis of these distributions combined with chemical common sense allowed to select atom types and, therefore, contacts used for the van der Waals radii determination. The main requirements were: (1) there are enough contacts to determine D _max so that line‐of‐sight contacts distribution contains a line‐of‐sight peak that is similar to the Gaussian function; (2) contact corresponds to non‐specific interaction; (3) influence of steric effects on A ⋅⋅⋅ B distance can be excluded; (4) addition of the contact to the list of contacts used for van der Waals radii determination does not change any radius significantly (>0.05 Å). This selection is subjective to a certain degree, however, it's well suited for our final goal which was to obtain R _vdW corresponding to weak nonspecific interactions that are not affected by any effects. Selected contact types were used for R _max determination and are marked with ‘+’ sign in the second column of Table S1. Using the data of Table S1 together with the data on intermolecular contacts28 allows one to reproduce this work, or to choose another set of contact types to determine another version of R _max.

Quantum chemical calculations were performed with the Gaussian 16 rev. B.0129 program at the B3LYP/6‐311++G(d,p) level of theory. The NCIS analysis was performed with the Multiwfn package.30 Geometry of the H₃N ⋅⋅⋅ CH₃F complex was obtained by merging optimized NH₃ and CH₃F molecules into the staggered C_3v structure with D(N ⋅⋅⋅ C)=3.0 Å. The N ⋅⋅⋅ C−F angle was changed so that the H₃N ⋅⋅⋅ CH₃F complex retains the N ⋅⋅⋅ (H)C−F symmetry plane. NCI surface (0.5 isosurface value) dependence on N ⋅⋅⋅ C−F angle remains unchanged with D(N ⋅⋅⋅ C) increasing.

Supporting information

As a service to our authors and readers, this journal provides supporting information supplied by the authors. Such materials are peer reviewed and may be re‐organized for online delivery, but are not copy‐edited or typeset. Technical support issues arising from supporting information (other than missing files) should be addressed to the authors.

Supplementary

I. Y. Chernyshov, I. V. Ananyev, E. A. Pidko, ChemPhysChem 2020, 21, 370.