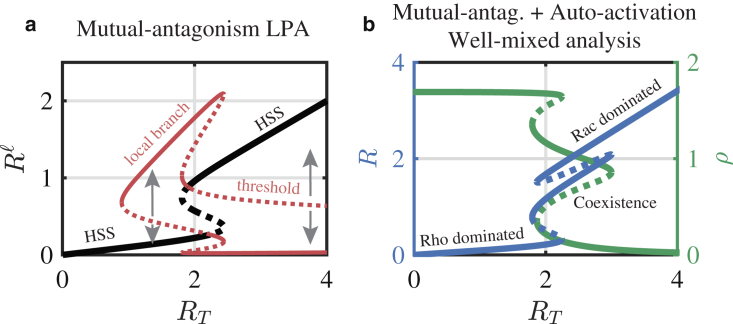
Figure 3.

Bistability, tristability, and polarization. (a) LPA bifurcation analysis of the mutual antagonism model (a = 0, similar to results in (43)) is shown. The global (black curve) and local solution branches (red curve) are shown along with their stability (solid, stable; dashed, unstable). A region of well-mixed bistability is enclosed in a larger region where stimulus induced polarization is possible (via a perturbation across a threshold). Gray arrows illustrate how a local perturbation $R^{\ell }$ may induce a response. A perturbation from the HSS may drive system to the local branch or may be insufficient to induce a response. In the former case, the LPA predicts that the perturbation will grow to the local branch driving pattern formation. Note also that as the parameter R_T changes, the global branch changes stability at the points where the local branch bifurcates, indicating the possibility for spontaneous pattern when the HSS becomes linearly unstable. Parameters are b = 1, c = 0, s = 0.5, n = 3, and ρ_T = 2. (b) Well-mixed bifurcation analysis of the mutual antagonism and autoactivation model (a > 0) is shown. Tristability is possible with both autoactivation and mutual antagonism. The middle branch is referred to as the coexistence HSS, with both Rac and Rho activity are at moderate levels. Parameters are a = 1.8, b = 4, c = 0, s = 0.5, n = 3, and ρ_T = 2. To see this figure in color, go online.