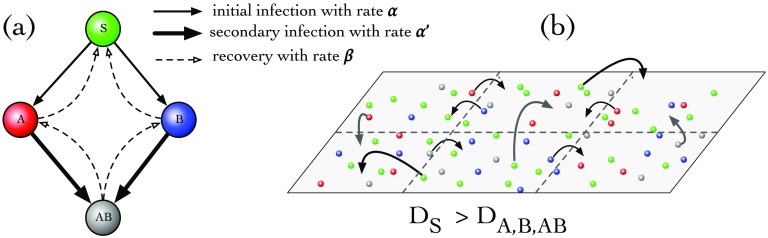
FIG. 1.

The model of interacting contagions. (a) Mean-field model (without space): Consider two infections, A and B, that circulate in a population. Four states are then possible for host individuals: susceptible S, partially infected A or B, and the coinfected state AB. In the contagion process, S becomes partially infected (A/B) with an initial infection rate $\alpha$ by contacting the infected; the partially infected individuals can be further be infected by the other infection to be doubly infected (AB) with the secondary infection rate ${\alpha }^{\prime }$. All infected individuals recover with rate $\beta$. (b) Spatially interacting contagions: When subpopulations are coupled through their spatial neighborhood, the diffusion captures the local mobility of individuals and thus also the infections they carried. Generally, the mobility of a given individual depends on its state; e.g., in epidemic spread, susceptible people statistically move faster than infected individuals, who might prefer to stay at home or in the hospital for recovery. Mathematically, this is captured by $D_S>D_{A,B,AB}$ within the RD framework described by Eq. (2).