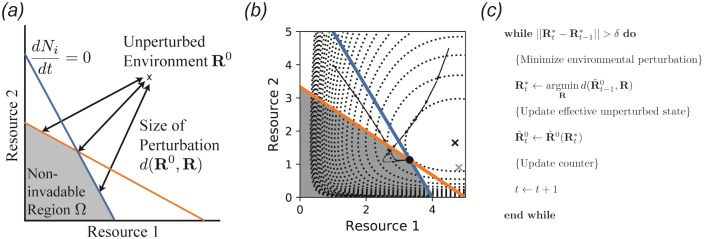
Fig 5. An expectation-maximization algorithm for finding noninvadable stationary states.

(a) Noninvadable states by definition can only exist in the region Ω of resource space where the growth rate dN_i/dt of each species i is zero or negative. Here, the blue and orange lines represent the combinations of resource abundances leading to zero growth rate for two different consumer species, so the noninvadable region is the space beneath both of the lines. Within this region, a recently discovered duality implies that the stationary state R* locally minimizes the dissimilarity d(R⁰, R) with respect to the fixed point R⁰ of the intrinsic environmental dynamics [23, 24]. (b) Metabolic byproducts move the relevant unperturbed state from R⁰ (gray ‘x’) to ${\tilde{\mathbf{R}}}^0\left(\mathbf{R}\right)$ (black ‘x’), which is itself a function of the current environmental conditions. Dotted contour lines represent $d({\tilde{\mathbf{R}}}^0\left({\mathbf{R}}^{*}\right),\mathbf{R})$, and arrows are two trajectories of the population dynamics starting from the unperturbed environmental state with two different sets of initial consumer population sizes. See main text and Appendix for model details and parameters. (c) Pseudocode for self-consistently computing R* and ${\tilde{\mathbf{R}}}^0\left({\mathbf{R}}^{*}\right)$, which is identical to standard expectation-maximization algorithms employed for problems with latent variables in machine learning.