Fig. 2. Micromechanics model illustrating similar flexural stiffness in an ultrathin, high-modulus tube as in a thicker, low-modulus tube.

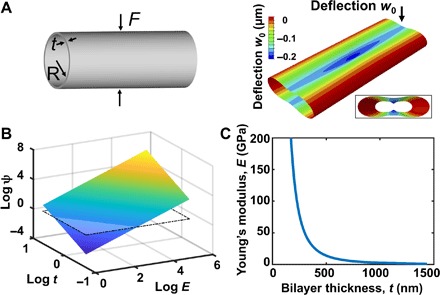
(A) Left: Schematic of a thin long elastic tube compressed by two equal and opposite radial loads. Right: Finite element snapshot showing the deflection of the tube when a force of 13.2 μN is applied to a tube with a thickness of 1.2 μm. The inset shows the front view of the deformed cylindrical shell. The deflection was enlarged 500 times for visualization. (B) 3D natural log plot of flexural stiffness (ψ; unit: N/m), for tubes with a range of Young’s moduli (E; 1 to 200 GPa) and wall thicknesses (t; 0.5 to 2 μm). The inserted plane shows the flexural stiffness calculated on the basis of Eq. 2, using values from hSMPA (t = 30 μm and E = 500 kPa). The plot shows that a tube composed of a thin wall with a high modulus can have the same compliance as a thicker tube with a low modulus. (C) Analytical predictions of the combination of the wall thickness (t) and Young’s modulus (E) for tubular constructs that yield the same flexural stiffness (ψ) as biological hSMPA (t = 30 μm and E = 500 kPa). The plot illustrates that tubes with wall thicknesses below ~500 nm can be composed of stiff wall materials and yet achieve the same flexural stiffness as thick-walled tubes composed of ultrasoft materials such as hydrogels or the cells and extracellular matrix of native blood vessels.