Fig. 3. Perturbation of the ZEBS in 1-UC FeSe by temperature, a neighboring Fe adatom, and different tunneling barriers.

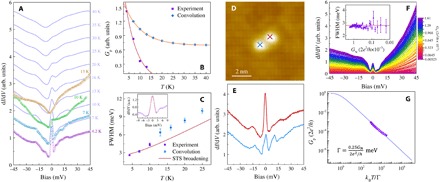
(A) Temperature dependence of the experimental tunneling spectra (open symbols) measured upon the Fe-adatom center in Fig. 2A and the convoluted 4.2-K spectra (solid curves) by Fermi-Dirac distribution function at higher temperatures (both vertically offset for clarity). (B) ZBC, G_p, plotted as a function of temperature (solid symbols) extracted from (A). (C) FWHM of the ZBCP (solid symbols) in the experimental and convoluted spectra of (A). The solid curve is the spectral energy resolution combining both instrumental and thermal broadening, $\mathrm{∆}E=\sqrt{{(2.5e V_{\text{mod}})}^2+{(3.5 k_{\mathrm{B}}T)}^2}$. Inset: Exemplifying the Gaussian fitting to the ZBCP, which defines the FWHM and error bars standard deviations adopted throughout. (D) Topographic image of an Fe-adatom dimer (8 nm × 8 nm; set point: V = 0.1 V, I = 500 pA). (E) Tunneling spectra (vertically offset for clarity) taken upon the Fe adatoms in (D). (F) Tunneling barrier conductance G_N dependence of the ZEBS spectra (4.2 K), where G_N is parameterized as the tunneling conductance (G_N = I/V). Inset: FWHM of the ZBCP in the main-panel spectra under different G_N. The solid curve is ΔE at 4.2 K. (G) Scaling analysis of G_p of the tunneling spectra of (F). Solid curve, calculated G_p for the MZM at different k_BT/Γ according to Eq. 1; solid symbols, experimental G_p plotted as a function of G_N rescaled as k_BT/Γ to match the calculated curve, yielding $\mathrm{\Gamma }=\frac{0.25{\mathit{G}}_{\mathrm{N}}}{2e^2/h} \text{meV}$.