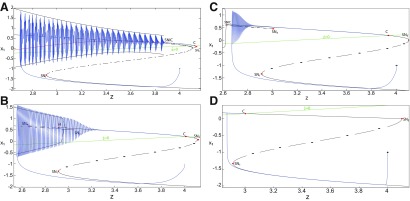
Figure 16.

Stabilizing the equilibrium point of the nonoscillatory state and DB. The Epileptor model remains in the ictal nonoscillatory state after a fast discharges period. We plot a (z, x₁) bifurcation diagram for different values of m, x₀ and I_ext2. A–C, I_ext2 = 0.45, m  =  0 and x₀ = −0.9 (A), I_ext2 = 0, m = −0.5, and x₀ = −0.8 (B), and I_ext2 = 0, m = −1, and x₀ = −0.8 (C). The equilibrium point C is a stable focus for A–C. The Epileptor stabilizes its equilibrium point C after transient seizure-like fast discharges, which disappear through a SNIC bifurcation (A) and a through Hopf bifurcation (B). The branches description for A–C is provided in Figures 5, 7, and 8, respectively. D, We plot a (z, x₁) bifurcation diagram with respect to z for m = −8 and I_ext2 = 0. The Z-upper (dashed), Z-middle (dash-dotted), and Z-lower (solid) branches consist of stable nodes, saddles, and stable nodes, respectively. Let x₀ = −0.6, the z-nullcline ($\dot{z}=0$) intersects the Z-upper branch at C, which is a stable node. The Epileptor model remains in DB after a transient NS. For all deterministic simulations: I.C = [−1 −5 4 0 0 0.01]. r  =  0.00095 and T_s = [0:0.001:2000] for A; r  =  0.002 and T_s = [0:0.001:2000] for B; r  =  0.001 and T_s = [0:0.001:2000] for C; and r  =  0.00005 and T_s = [0:0.001:3000] for D.