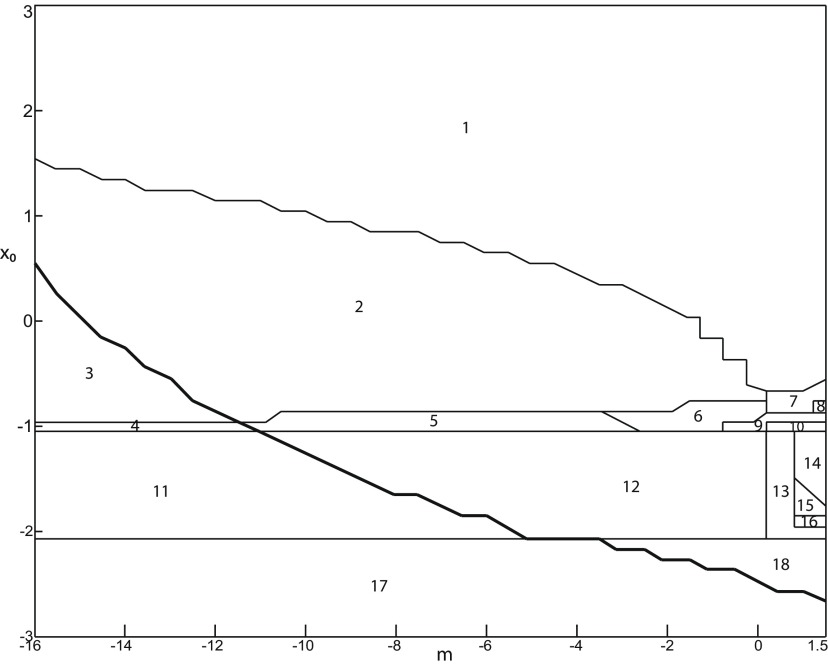
Figure 32.

The Epileptor parameter space of equilibrium points and periodic orbits with respect to the parameters m and x₀ ($I_{ext2}=0.45$). There are 18 areas separated by a SNPO bifurcation (bold line). LC exists above and it does not exist below. The z-nullcline intersects the (z, x₁) curve at different equilibrium points. The equilibrium point is an unstable focus for areas 1 through 3. The equilibrium points are a stable node, an unstable focus and a saddle in areas 4 and 5. The equilibrium points are a stable focus, an unstable focus, and a saddle in area 6. The equilibrium points are one saddle and two unstable foci in area 7. The equilibrium points are a saddle, an unstable focus, and an unstable node in area 8. The equilibrium points are one unstable focus and two saddles in area 9. The equilibrium points are three saddles in area 10. The equilibrium point is a saddle for areas 11 through 16. The equilibrium point is a stable node in areas 17 and 18. In areas 1, 7, 8, 9, 10, and 14, only LC exists. Area 2 presents bistability of LC and SLC. In area 3, only SLC exists. In area 4, only a nonoscillatory state exists. In areas 5 and 6, LC and a nonoscillatory state coexist. Only SLE exists in area 11, and coexists with LC in areas 12 and 13. SLE occurs through a fold/circle bifurcation in areas 11 and 12, and through a fold/homoclinic bifurcation in area 13. NS exists in area 17 and coexists with LC in area 18. In areas 15 and 16, LC coexists with a chaotic state which is periodic in area 15, and it does not in area 16.