Whitening of odor representations by the wiring diagram of the olfactory bulb

Abstract

Neuronal computations underlying higher brain functions depend on synaptic interactions among specific neurons. A mechanistic understanding of such computations requires wiring diagrams of neuronal networks. We examined how the olfactory bulb (OB) performs ‘whitening’, a fundamental computation that decorrelates activity patterns and supports their classification by memory networks. We measured odor-evoked activity in the OB of a zebrafish larva and subsequently reconstructed the complete wiring diagram by volumetric electron microscopy. The resulting functional connectome revealed an overrepresentation of multisynaptic connectivity motifs that mediate reciprocal inhibition between neurons with similar tuning. This connectivity suppressed redundant responses and was necessary and sufficient to reproduce whitening in simulations. Whitening of odor representations is therefore mediated by higher-order structure in the wiring diagram that is adapted to natural input patterns.

Neuronal activity patterns evoked by natural stimuli are transformed in the brain to extract relevant information. At early processing stages, activity patterns often contain correlations and intensity variations that originate from the statistics of natural scenes and from the tuning of sensory receptors¹. This statistical structure complicates the classification of sensory inputs because it does not usually reflect behaviorally relevant stimulus categories². For example, visual scenes may be dominated by a large number of pixels representing sky while the biologically most important information is conveyed by a small subset of pixels representing specific objects (e.g., a hawk or a sparrow). Hence, correlations in sensory inputs can complicate meaningful pattern classification and object recognition. This problem can be alleviated by whitening, a fundamental transformation in signal processing that decorrelates patterns and normalizes their variance. Whitening is therefore often used early in a pattern classification process to remove undesired correlations and to optimize the use of coding space³.

In the visual and auditory systems, whitening of individual neurons’ responses to natural stimuli supports efficient coding by redundancy reduction^4–7. Efficient pattern classification, however, requires whitening of activity patterns across neuronal populations. This form of whitening occurs in the olfactory bulb (OB)^8–10 where axons of olfactory sensory neurons expressing the same odorant receptor converge onto discrete glomeruli. Odors evoke distributed patterns of input activity across glomeruli that can overlap substantially when odorants share functional groups^11–13. The variance (contrast) of these glomerular activity patterns varies dramatically as a function of odor concentration. The output of the OB is transmitted to higher brain areas by mitral cells (MCs), which receive sensory input from individual glomeruli and interact with other MCs cells via multisynaptic interneuron (IN) pathways (Fig. 1a). Unlike glomerular inputs, activity patterns across MCs become rapidly decorrelated during the initial phase of an odor response^8,14–18 and their variance depends only modestly on stimulus intensity^10,19. Neuronal circuits in the OB therefore decorrelate and normalize population activity patterns, resulting in a whitening of odor representations. Pattern decorrelation predicted learning in odor discrimination tasks^9,16, consistent with the assumption that whitening facilitates pattern classification. However, it remains unclear how this transformation is achieved by interactions between neurons in the OB network.

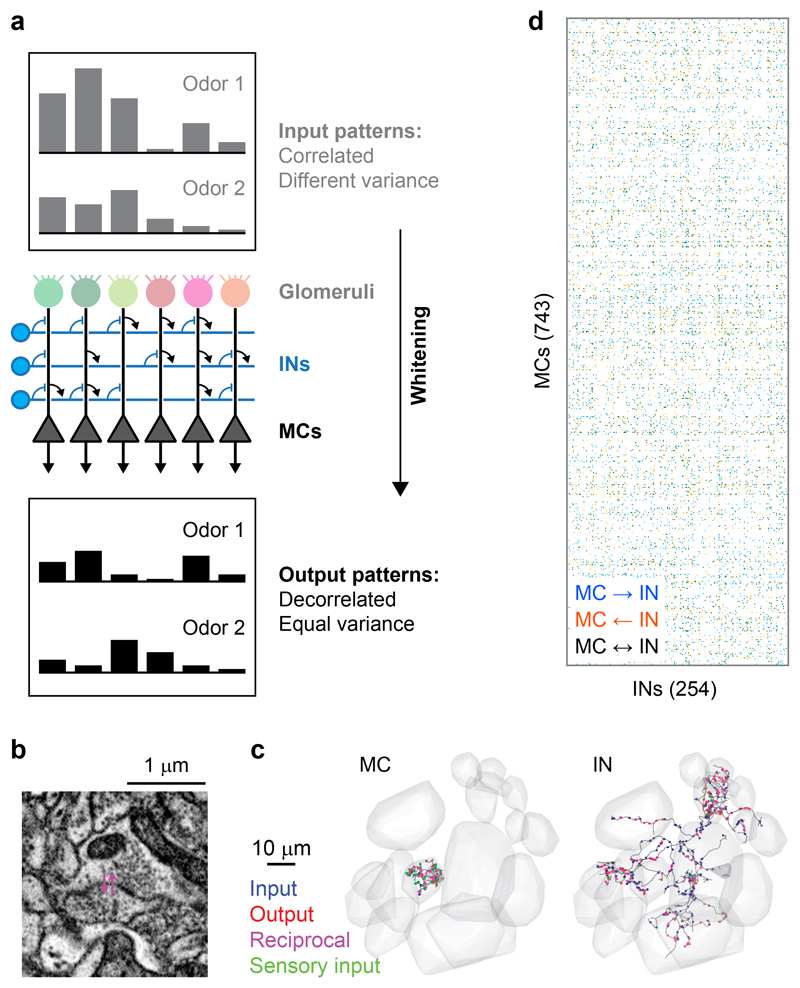
Fig. 1. Neuronal organization and computations in the OB.

a, Schematic illustration of whitening in the OB. Top: correlated input patterns with different variance. Bottom: decorrelated output patterns with similar variance. Center: Highly simplified illustration of the OB circuit. MCs receive excitatory input from a single glomerulus and interact via inhibitory INs. Whitening requires multisynaptic interactions between specific subsets of MCs that are mediated by INs and defined by the wiring diagram. Interactions between INs and top-down inputs to the OB are not shown. b, Example of a reciprocal synapse between a MC and an IN. c, Reconstructions of a MC (left) and an IN (right). Gray volumes show glomeruli, dots depict synapses, colors denote synapse class (unidirectional non-sensory input [blue], unidirectional output [red], reciprocal [magenta], input from sensory neurons [green]). d, Simplified representation of the wiring diagram between MCs and INs (binarized connection strength). Colored matrix elements show MC→IN synapses (blue), MC←IN synapses (orange), and reciprocal synapses (black).

Efficient whitening can be achieved by transformations that are adapted to the correlation structure of input patterns¹. Such adaptive whitening requires prior knowledge about inputs and tuning-dependent connectivity between specific cohorts of neurons. Hence, whitening of sensory representations is thought to depend on an evolutionary memory of stimulus space that is contained in the wiring diagram of neuronal circuits. This hypothesis is difficult to test in the OB because tuning and functional connectivity cannot be inferred from topographical relationships between neurons^11,20–22. Moreover, because interactions between MCs are multisynaptic via INs, relevant inhibitory interactions cannot be visualized by transsynaptic tracing across a single synapse.

Adaptive whitening and other memory-based processes are likely to depend on higher-order features of neuronal connectivity that cannot be detected by sparse sampling of pairwise connections. We therefore used a “functional connectomics” approach that combines population-wide neuronal activity measurements with dense reconstructions of wiring diagrams, taking advantage of the small size of the larval zebrafish brain. We first measured odor responses of neurons in the OB by multiphoton calcium imaging and subsequently reconstructed the synaptic connectivity among all neurons by serial block-face scanning electron microscopy (SBEM)^23–26. We found that higher-order features of multisynaptic connectivity specifically suppress the activity of correlated MC ensembles in a stimulus-dependent manner, resulting in a decorrelation and variance normalization. The wiring diagram of the OB is therefore adapted to the correlation structure of its inputs and mediates a whitening operation based on contrast reduction rather than contrast enhancement.

Results

Reconstruction of the wiring diagram and mapping of neuronal activity

We previously reconstructed the skeletons of 1’003 neurons in an SBEM image stack of the OB from a zebrafish larva (4.5 days post fertilization), accounting for 98% of all neurons in the OB, and classified them as MCs (n = 745), INs (n = 254) and “atypical projection neurons” (n = 4)^25,26. We now annotated the synaptic connections of these neurons to reconstruct the full wiring diagram of the OB. Human annotators followed each of the reconstructed skeletons and manually labeled all input and output synapses (Fig. 1b,c). Subsequently, synapses of INs were annotated again by different annotators. Hence, each synapse involved in MC-IN-MC connectivity motifs should have been encountered at least three times. To obtain a conservative estimate of the wiring diagram with few false positives we retained only those synapses that were annotated at least twice by independent annotators.

Each synapse was assigned a unitary weight so that the total connection strength between a pair of neurons equaled the number of synapses. The resulting wiring diagram contained 19,874 MC→IN synapses, 17,524 MC←IN synapses (Fig. 1d), and 13,610 synapses between INs. We also observed contact sites between MCs associated with the same glomerulus where plasma membranes showed strong staining but these sites usually lacked vesicles. We did therefore not consider synaptic connections between MCs. Axons of sensory neurons frequently made synapses onto MCs but synapses onto INs were rare (Extended Data Fig. 1a)²⁶.

On average, connected pairs of MCs and INs made 3.1 MC→IN synapses and 2.9 MC←IN synapses per pair, and pairs of connected INs made 2.6 synapses per direction. A hallmark of synaptic connectivity in the adult OB are reciprocal dendrodendritic synaptic connections between the same MC-IN pair. In the larval OB, 52% of MC→IN synapses and 51% of MC←IN synapses were associated with a synapse of opposite direction, usually within 2.5 μm, between the same pair of neurons (Fig. 1b). Hence, reciprocal synaptic connectivity is prominent already in the larval OB of zebrafish.

Prior to preparation of the OB sample for SBEM we measured neuronal activity by multiphoton imaging of the calcium indicator GCaMP5, which was expressed under the pan-neuronal elavl3 promoter²⁷. Somata observed in electron microscopy were mapped onto the light microscopy data using an iterative landmark-based affine alignment procedure followed by manual proofreading (Fig. 2a,b; Extended Data Fig. 1b). Somatic calcium signals evoked by four amino acid odors (10^-4 M) and four bile acid odors (10^-5 M) were measured sequentially in six optical planes (Fig. 2a-c; Extended Data Fig. 2) and temporally deconvolved to estimate odor-evoked firing rate changes²⁸. The dynamics of neuronal population activity was then represented by time series of activity vectors for each odor stimulus (232 MCs and 68 INs).

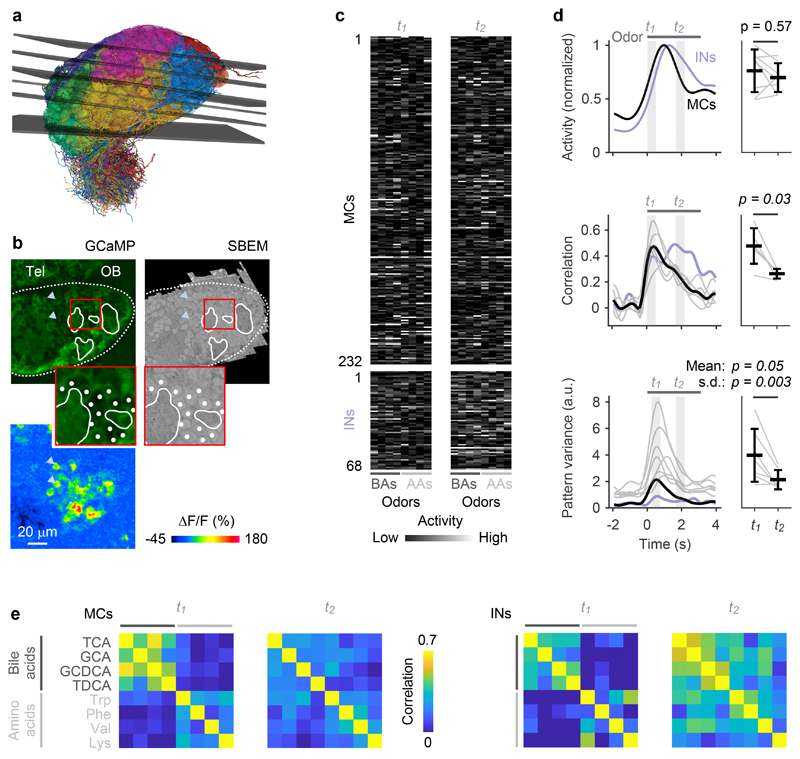
Fig. 2. Odor-evoked population activity in the OB.

a, Mapping of the six optical image planes selected for calcium imaging onto the EM-based reconstructions of neurons. Thickness of planes shows range of drift between trials. b, One optical image plane showing raw GCaMP5 fluorescence (left) and the corresponding oblique slice through the EM image stack (right). Dashed line outlines ipsilateral brain hemisphere; continuous white outlines show glomerular neuropil. Tel, telencephalon; OB, olfactory bulb. Region outlined by the red square is enlarged; white dots depict somata in corresponding locations. Bottom left: fluorescence change evoked by an odor stimulus in the same field of view. Arrowheads depict locations of two responsive somata in different images. The alignment of EM images with optical images was repeated in all n = 6 image planes with similar results. c, Activity (deconvolved calcium signals) of MCs (n = 232) and INs (n = 68) in response to four bile acids (BAs) and four amino acids (AAs) during two time windows, t₁ and t₂. d, Left: time courses of odor-evoked activity (n = 8 odors), pattern correlation (Pearson; n = 6 bile acid pairs) and pattern variance (n = 8 odors). Activity was determined by low-pass filtering and deconvolution of somatic calcium signals. Horizontal bar indicates time of odor stimulation. Black: mean measures across MCs. Gray: individual odors (variance) or odor pairs (correlation). Light blue: mean measures across INs. Correlation was measured only between activity patterns evoked by bile acids because patterns evoked by amino acids were dissimilar already at response onset. Right: Mean measures for MCs during t₁ and t₂ (activity, correlation, mean variance: two-sided Wilcoxon rank-sum test; s.d. of variance: F-test with df1 = df2 = 7 degrees of freedom; F = 14.0). Black markers and error bars show mean ± s.d.; gray lines show individual datapoints. e, Matrices showing Pearson correlations between activity patterns across MCs (left; n = 232) and INs (right; n = 68) at t₁ and t₂. Odors: TCA, taurocholic acid; GCA, glycocholic acid; GCDCA, glycochenodeoxycholic acid; TDCA, taurodeoxycholic acid; Trp, tryptophan; Phe, phenylalanine; Val, valine; Lys, lysine.

Decorrelation and contrast normalization of activity patterns across MCs have been characterized previously in the OB of adult zebrafish^8,14,15 and mice^16–18 where >90% of neurons are GABAergic INs. In the larval OB, in contrast, INs account for only 25% of all neurons²⁶. Most of these INs are likely to be periglomerular and short axon cells because INs with the typical morphology of granule cells appear only later in development. We therefore asked whether the core circuitry present in the larval OB already performs computations related to whitening.

Correlations between activity patterns evoked by different bile acids were high after stimulus onset and decreased during the subsequent few hundred milliseconds (Fig. 2d,e). Patterns evoked by amino acids, in contrast, were less correlated throughout the odor response, which was expected because most amino acids had dissimilar side chains. Further analyses of pattern decorrelation therefore focused on activity patterns evoked by the four bile acids while other analyses included all eight odors. To quantify pattern decorrelation we computed the mean difference in pairwise Pearson correlations between a time window shortly after response onset (t₁) and a later time window (t₂) that was chosen so that the mean population activity across MCs was not significantly different from t₁ (Fig. 2d; p = 0.57, Wilcoxon rank-sum test). Pattern correlations across MCs, however, were significantly lower at t₂ than at t₁ (p = 0.03, Wilcoxon rank-sum test), demonstrating that MC activity patterns were reorganized and decorrelated. Activity across INs followed the mean MC activity with a small delay and did not exhibit an obvious decorrelation during the early phase of the odor response (Fig. 2d). These findings are consistent with observations in the adult OB²⁹. The natural time course of olfactory input to the OB of zebrafish larvae is likely to be slow because animals live in slow waters close to the substratum³⁰ and because the temporal resolution of their olfactory sensory neurons is low³¹. We therefore assume that the dynamics of odor-evoked population activity in the OB is fast compared to the kinetics of natural sensory inputs.

The contrast of MC activity patterns, as measured by the variance of activity across the population, increased shortly after stimulus onset and peaked slightly later than pattern correlation. Subsequently, variance decreased and became more uniform across odors, as reflected by a significant decrease in the standard deviation (s.d.) of the variance across odors between t₂ and t₁ (Fig. 2d; p = 0.003, F-test; t₁ was slightly shifted relative to the time window for correlation analysis to cover the peak of the variance). Hence, MC activity patterns in the larval OB became decorrelated and contrast-normalized, consistent with the whitening of odor representations in the adult OB.

Whitening can facilitate pattern classification but may also introduce noise. We therefore quantifed the reliability of odor classification using a template matching procedure based on single-trial responses and found that classification success, as well as the separation of correct and incorrect classifications, were slightly higher at t₂ than at t₁ (Extended Data Fig. 3). Hence, pattern decorrelation did not compromise the reliability of odor identification by a simple classifier but facilitated pattern separation.

Computational consequences of connectivity

While contrast normalization can be achieved by global scaling operations such as divisive normalization³², pattern decorrelation requires interactions between distinct subsets of neurons⁹. In theory, pattern decorrelation could be achieved by large networks with sparse and random connectivity³³ but this architecture is inconsistent with the low number of INs in the larval OB. Smaller networks can decorrelate specific input patterns when their connectivity is adapted to the covariance structure of these inputs, suggesting that decorrelation in the OB is an input-specific transformation of odor representations that is encoded in the wiring diagram. In order to explore this hypothesis we first asked whether whitening can be reproduced by implementing the wiring diagram in a network of minimally complex single-neuron models (Fig. 3a).

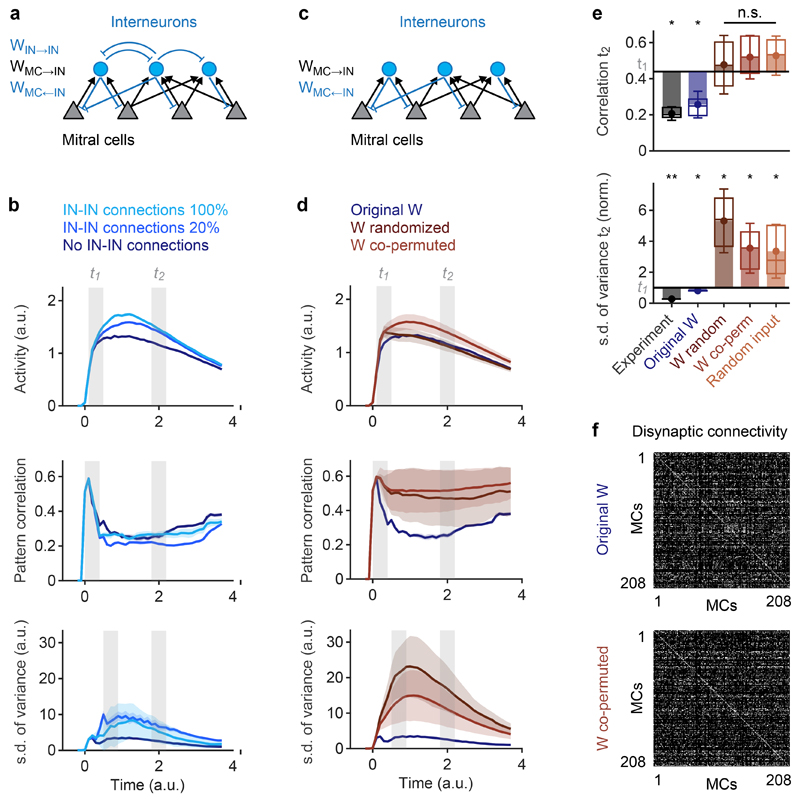
Fig. 3. Whitening depends on connectivity.

a, Architecture of the simulated network. Sensory input was targeted to MCs but not to INs. b, Time courses of simulated odor-evoked activity, pattern correlation (Pearson) and the s.d. of pattern variance obtained with different IN-IN connection strengths (100%, 20%, 0%). 100% corresponds to the same strength as MC←IN connections. Measures were calculated across all n = 208 MCs. c, Simulated network without IN-IN connections. d, Time courses of simulated activity, pattern correlation (Pearson) and s.d. of pattern variance obtained with different wiring diagrams (no IN-IN connections). Measures were calculated across all n = 208 MCs. Blue: original wiring diagram obtained by circuit reconstruction. Dark red: fully randomized connectivity. Light red: co-permutation of feed-forward (MC→IN) and feed-back (MC←IN) connectivity. Shaded areas show s.d. across permutations. e, Pattern correlation and s.d. of pattern variance at t₂. Horizontal black lines show mean experimental values at t₁; s.d. of pattern variance is normalized to the experimental value at t₁. Statistical comparisons of correlation and s.d. of variance were performed using a two-tailed t-test and an F-test, respectively. Dots show means, error bars show s.d., filled bars show difference to corresponding values at t₁, box plots show median, 25% percentile, and 75^th percentile. For experimental results and simulations using the reconstructed wiring diagram, variability was measured across odor pairs (correlation; bile acids only; n = 6) or individual odors (s.d. of variance; n = 8). Significance tests compare values at t₂ to experimental values at t₁ (correlation: two-sided Wilcoxon rank-sum test; s.d. of variance: F-test with df1 = df2 = 7 degrees of freedom). For other simulation results, variability was measured across n = 50 different network simulations (repetitions). Significance tests compare repetitions to the mean value observed experimentally at t₁ (two-tailed t-test with 49 degrees of freedom). *, p < 0.05; **, p < 0.01; ***, p < 0.001; n.s., not significant. P-values: correlation: 0.03, 0.04, 0.81 (t = 0.23), 0.51 (t = 0.66), 0.42 (t = 0.81); s.d. of variance: 0.003 (F = 14.0), 0.04 (F = 5.2), 0.01 (t = 2.56), 0.03 (t = 2.19), 0.03 (t = 2.18). f, Top: disynaptic connectivity matrix between all MCs included in activity measurements and simulations (W_MC→IN * W_MC←IN; Methods). Grayscale represents number of disynaptic MC-IN-MC connections (normalized). Bottom: example of a disynaptic connectivity matrix with the same order of MCs after co-permuting W_MC→IN and W_MC←IN.

We first simulated a network of threshold-linear rate neurons with 208 MCs, representing all recorded MCs with input and output synapses, and 234 INs, representing all connected INs. Connections between individual neurons were given by the wiring diagram. Excitatory sensory input into MCs was defined by the odor-evoked activity pattern at t₁. INs received no sensory input because synapses from sensory neurons onto INs were rare (Extended Data Fig. 1a). All connections made by neurons of the same type (MC or IN) had the same weight scaling. The time course of stimuli consisted of a fast initial rise followed by a slow decay³³, approximating the response time course of olfactory sensory neurons in zebrafish⁸. Because connectivity was fixed, the final network model had only six degrees of freedom (thresholds, synaptic weight scaling factors and time constants of each neuron type).

Correlations between simulated population responses to bile acids increased rapidly and subsequently decreased. Consistent with experimental observations, the mean correlation decreased significantly between two time windows t₁ and t₂ that were chosen so that the mean activity was not significantly different (Fig. 3b). The variance (contrast) of activity patterns and its standard deviation across stimuli peaked slightly later than the correlation and decreased thereafter (Fig. 3b). Correlations between IN activity patterns remained higher than correlations between MC activity patterns throughout the odor response (Extended Data Fig. 4a). Hence, simulation results were in good agreement with experimental observations.

To examine the contribution of IN-IN connections to the observed pattern transformations we modified the strength of IN-IN synapses from 100% (same strength as MC←IN connections) to 0% (no IN-IN connections). Reducing IN-IN connection weights slightly decreased the mean activity, consistent with a disinhibitory effect of IN-IN connections, and slightly decreased pattern variance and its s.d.. Pattern decorrelation, however, remained almost unaffected (Fig. 3b). IN-IN connectivity was therefore omitted in further simulations for simplicity (Fig. 3c).

To exclude the possibility that pattern decorrelation by simulated networks reflects a chaotic process we examined responses to inputs with biologically realistic amounts of noise (Methods). While activity patterns representing different odors became decorrelated, correlations between noisy representations of the same stimuli remained high (Extended Data Fig. 4b), demonstrating that pattern decorrelation did not reflect an amplification of noise.

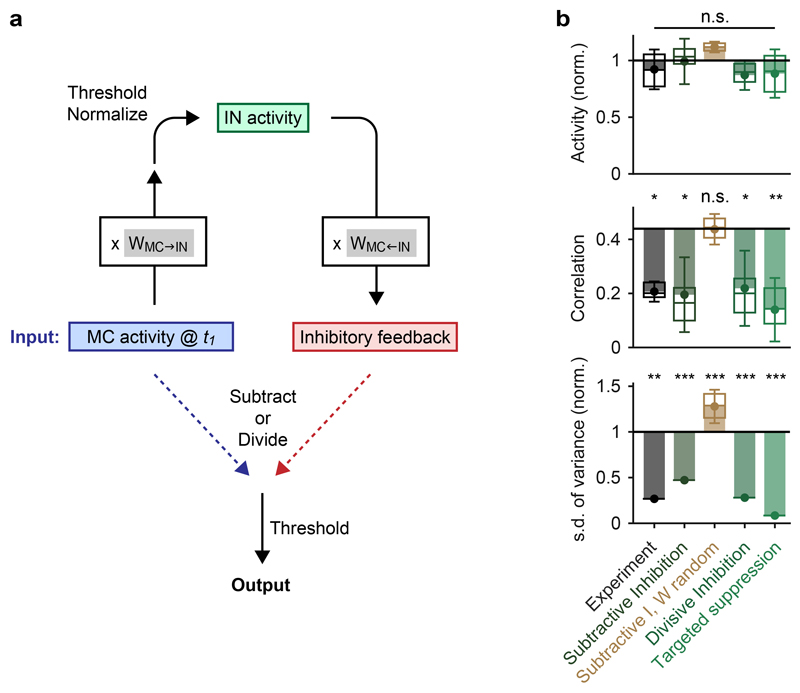
Randomizing the wiring diagram by independent shufflings of the feed-forward connectivity matrix W_MC→IN and the feedback connectivity matrix W_MC←IN abolished pattern decorrelation and contrast normalization (Fig. 3d,e). Hence, whitening depended on the wiring diagram. To corroborate this conclusion we examined whether the reorganization of activity patterns underlying whitening can be predicted from connectivity without an explicit simulation of network dynamics. Activity patterns at t₁ were multiplied with the feed-forward connectivity W_MC→IN, normalized, and thresholded to generate a hypothetical pattern of IN activity. This activity pattern was then multiplied with the feed-back connectivity W_MC←IN to predict the pattern of feedback inhibition onto MCs. The feedback pattern was either subtracted from the MC activity at t₁ (subtractive inhibition), or the MC activity pattern at t₁ was divided by the pattern of feedback inhibition neuron-by-neuron (divisive inhibition; Extended Data Fig. 5a). This simple algebraic procedure reproduced both pattern decorrelation and variance normalization, independent of whether inhibition was subtractive or divisive (Extended Data Fig. 5b). Whitening was again abolished when connectivity matrices were randomized. These results confirm that the wiring diagram contains information essential for whitening.

We next performed more specific manipulations to explore how whitening depends on higher-order structure in the wiring diagram. In simulations without IN-IN connections, we first applied the same shufflings to MC→IN connections (W_MC→IN) and to MC←IN connectivity (W_MC←IN). This co-permutation of feed-forward and feedback connectivity shuffles the off-diagonal elements in the disynaptic connectivity matrix (lateral inhibition) but preserves the overall distribution of disynaptic MC→IN→MC connection strengths and the on-diagonal elements (self-inhibition; Fig. 3f). Similar to the independent randomization of W_MC→IN and W_MC←IN, co-permutation of W_MC→IN and W_MC←IN abolished whitening (Fig. 3d,e). Moreover, whitening was abolished when input channels were permuted to produce novel input patterns with the same statistical properties and correlations (Fig. 3e). These results show that whitening is mediated by higher-order features of multisynaptic connectivity that are adapted to patterns of sensory input.

Higher-order structure of connectivity

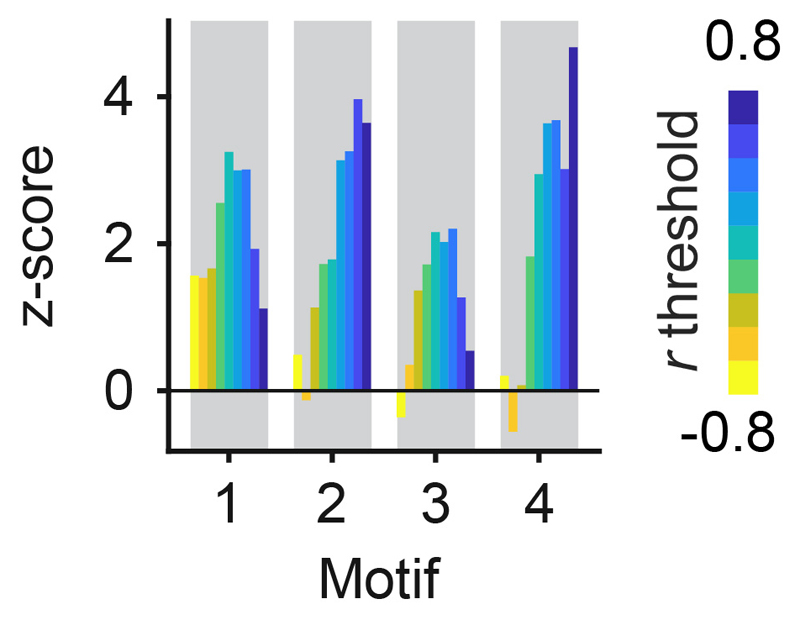
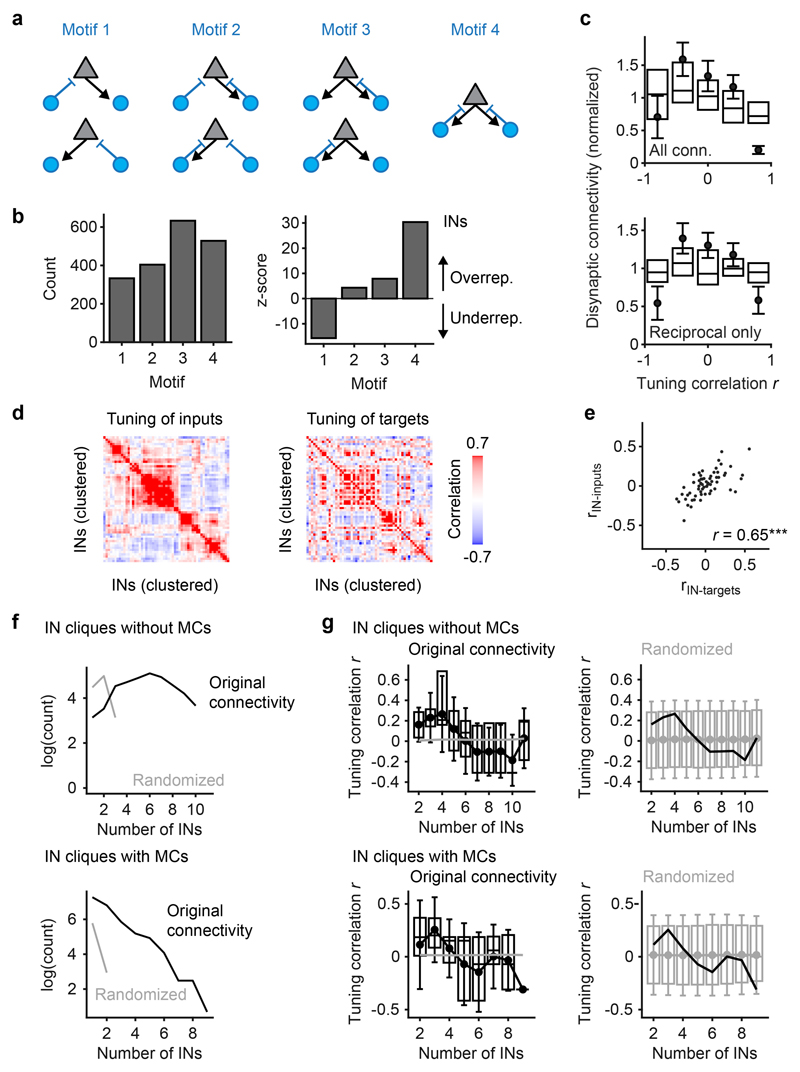
The shortest synaptic path between two MCs associated with different glomeruli is a disynaptic interaction via one IN (MC-IN-MC). To identify properties of the wiring diagram that mediate whitening we therefore analyzed MC-IN-MC triplets. There are seven possible triplet configurations that represent four topological motifs (Fig. 4a). We found that the motif containing no reciprocal connection (motif 1) was underrepresented whereas the other motifs were overrepresented in comparison to randomized networks (Fig 4b). The strongest overrepresentation was observed for motif 4, which contains reciprocal connections between both MCs and the IN. Hence, MC-IN-MC triplets frequently contained reciprocal connections.

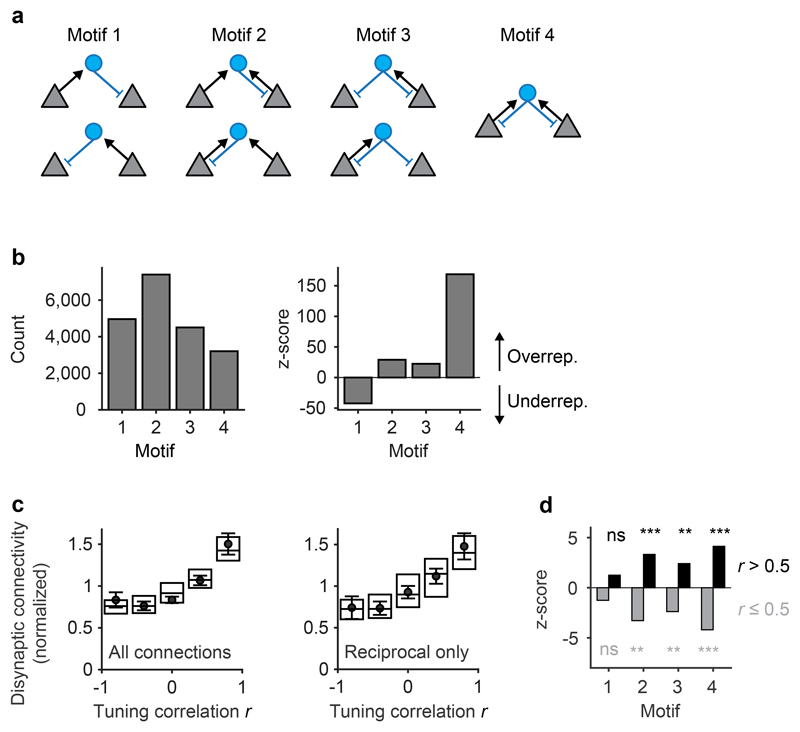
Fig. 4. Tuning-dependent disynaptic connectivity in the OB.

a, Classes of triplet connectivity motifs between MCs and INs. b, Left: number of connectivity motifs found in the wiring diagram (considering only MCs with activity measurements; n = 232). Right: z-score quantifying over- or under-representation of motifs as compared to 10,000 independent randomizations of the wiring diagram. c, Left: disynaptic connections between responsive MCs as a function of tuning similarity, normalized to the mean (n = 2,162 neuron pairs; Methods; number of neuron pairs per bin: 298, 368, 416, 502, 578). Dots and error bars show mean ± s.e.m. when tuning curves were determined using all eight odor stimuli. Box plots show median, 25^th percentile and 75^th percentile across results when tuning curves were determined by all possible combinations of four odors. Right: same analysis including only reciprocal connections (motif 4; n = 2,162 neuron pairs). d, Over- and under-representation of connectivity motifs among MC pairs with high tuning correlation (Pearson; r > 0.5; black) and among the remaining pairs (r ≤ 0.5; gray). Z-scores were determined by comparison against 10,000 shufflings of the tuning correlation matrix (one-tailed permutation test, n = 10,000 permutations, no adjustments for multiple comparisons). *, p < 0.05; **, p < 0.01; ***, p < 0.001; n.s., not significant. P-values for motif counts: 0.1117, 0.1105, 0.0015, 0.0014, 0.0122, 0.0109, 0.0001, 0.0004.

To determine whether disynaptic connectivity between MCs depends on their tuning we constructed an input tuning curve for each MC from the responses to the eight odors at t₁. We then quantified the Pearson correlation between the input tuning curves of MC pairs and the number of disynaptic MC-IN-MC connection paths across all motifs. The mean number of disynaptic connections increased with the input tuning correlation (Fig. 4c, left). MCs with similar tuning were more likely to be connected through motifs with reciprocal connections, particularly motifs 2 and 4 (Fig. 4d; Extended Data Fig. 6). Consistent with this observation, the correlation between tuning similarity and disynaptic connectivity of MC pairs remained strong when only reciprocal connections were considered (Fig. 4c, right). Hence, triplets mediate interactions preferentially between MCs with similar tuning, and these interactions frequently contain reciprocal connections.

As for MC-IN-MC connections, motifs with one or two reciprocal connections were also overrepresented in IN-MC-IN triplets but no simple relationship was apparent between input tuning and disynaptic IN-MC-IN connectivity (Extended Data Fig. 7a-c). In addition, we found that the tuning of synaptic inputs and outputs of individual INs was significantly correlated and that large sets of fully reciprocally connected neurons (“maximal cliques”) were strongly overrepresented in the wiring diagram (Extended Data Fig. 7d-g). These observations further demonstrate that the connectivity among OB neurons is not random but governed, at least in part, by functional response properties.

Mechanism of whitening

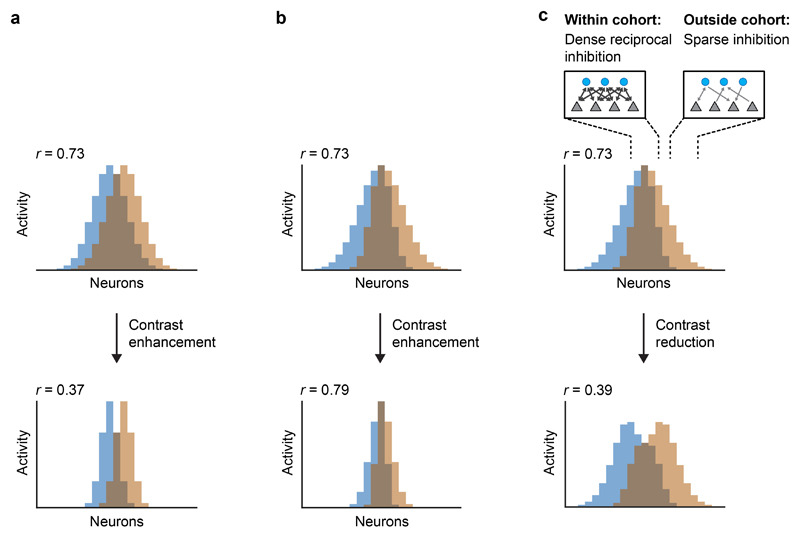
Unidirectional lateral inhibition between functionally related neurons sharpens tuning curves and enhances pattern contrast in the retina³⁴ and elsewhere (Fig. 5a, left). In idealized networks with reciprocal connectivity, in contrast, inhibition does not amplify asymmetries in inputs and self-inhibition is usually stronger than lateral inhibition (assuming equal synaptic strength; Fig. 5a, right). Hence, reciprocal triplet connectivity should primarily down-regulate, rather than sharpen, the activity of neurons in connected cohorts. As illustrated in Extended Data Fig. 8, computational effects of contrast enhancement (by unidirectional connectivity) or suppression of cohorts (by partially reciprocal connectivity) depend on the properties of input patterns. Contrast enhancement can decorrelate inputs when stimulus-specific information is contained in strong responses because strong responses are emphasized while weak responses are suppressed^4,34. However, when strong responses are non-specific, contrast enhancement fails to decorrelate patterns because it enhances non-informative responses while suppressing weaker, potentially informative responses. Under these conditions, patterns may be decorrelated by the selective suppression of strongly active cohorts, which can, in principle, be achieved by cohort-specific reciprocal inhibition (Extended Data Fig. 8).

Fig. 5. Disynaptic connectivity underlying feature suppression.

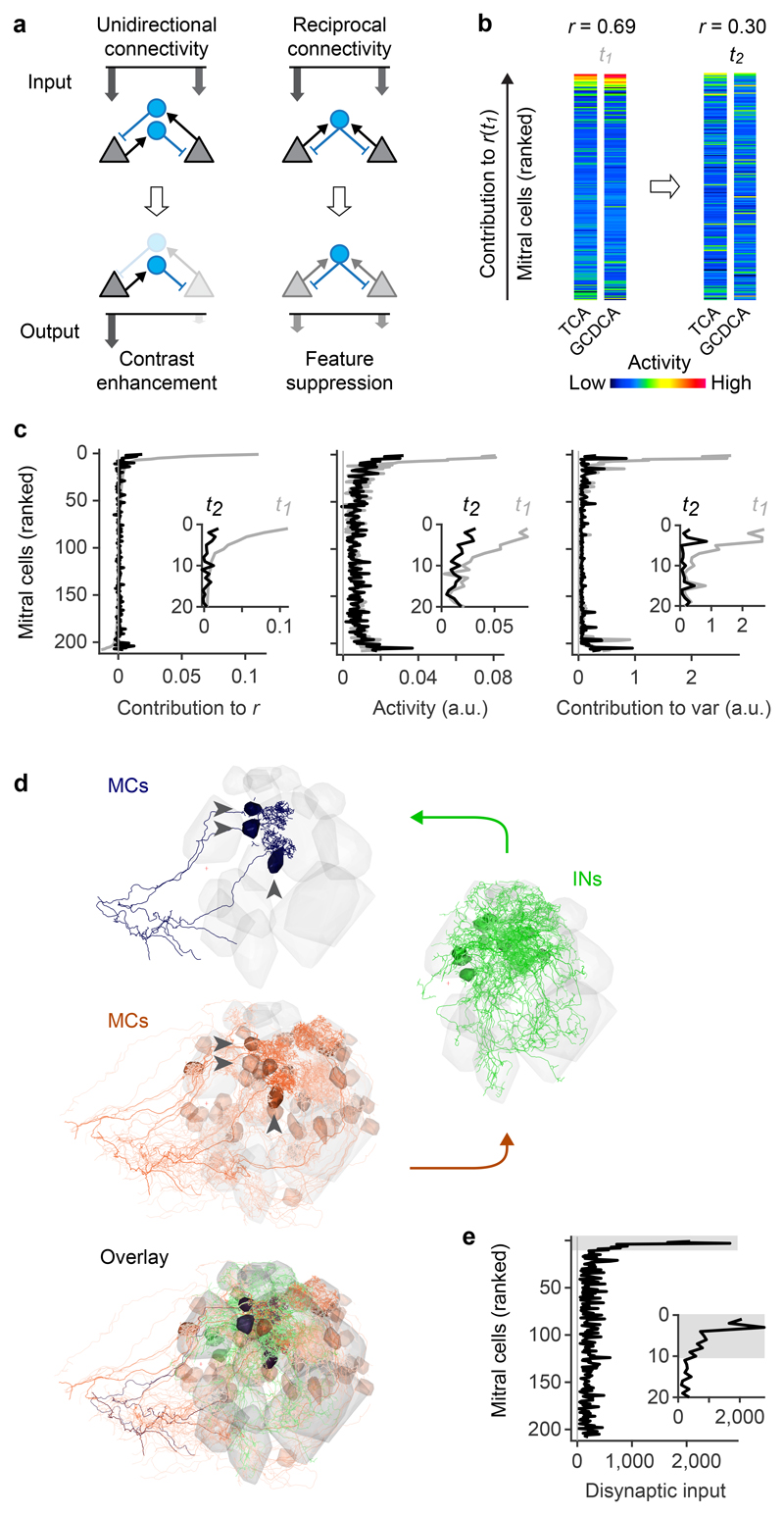
a, Schematic illustration of contrast enhancement by unidirectional lateral inhibition (left) and down-scaling of cohort activity by reciprocal inhibition (right; feature suppression). Arrow length and grayscale indicate activity. b, Example of MC activity patterns evoked by two bile acids (TCA, GCDCA) that were decorrelated between t₁ and t₂. MCs are ranked from top to bottom by their individual contribution to the pattern correlation r at t₁ (r_i,t1; Pearson correlation). c, Left: average contribution of MCs to all pairwise correlations between activity patterns evoked by bile acids at t₁ and t₂. MCs were ranked by r_i,t1 for each pair of patterns as in b. Sorted vectors of correlation contributions were then averaged over odor pairs. Center, right: Mean bile-acid evoked activity of MCs and mean contribution of MCs to pattern variance. MCs were sorted by r_i,t1 and averaged as in the left panel. Gray and black curves show correlation contribution, activity, and variance contribution at t₁ and t₂, respectively (same sorting of individual neurons by r_i,t1 for all curves). Insets enlarge the top part of the curves (20 MCs with highest r_i,t1). d, Example of disynaptic retrograde tracing of functional cohorts in the wiring diagram. Blue: three MCs with highest r_i,t1 for the odor pair shown in b (“starter MCs”). Green: 12 INs with largest number of synaptic inputs to the starter MCs. Red: 48 MCs with largest number of disynaptic inputs to the starter MCs. Transparency represents the number of synaptic connections. Note that the MCs with strong disynaptic connectivity to the starter MCs include the starter MCs themselves, consistent with pronounced reciprocal connectivity among functionally related MC cohorts. e, Disynaptic MC-IN-MC connectivity as a function of correlation contribution at t₁ (r_i,t1; same ranking of MCs as in b and c). For each pair of bile acids, the 10 MCs with the highest r_i,t1 were selected as starter cells. Disynaptic inputs from all MCs were then represented in a vector and averaged over odor pairs. Note strong overrepresentation of disynaptic connectivity within the cohort of starter cells (gray shading).

To examine the basis of pattern correlations in the OB we analyzed population activity patterns evoked by bile acids at t₁. For each pair of patterns, we quantified the contribution r_i,t1 of MC i to the Pearson correlation r and ranked MCs by their r_i,t1 (see example in Fig. 5b; rankings differed between odor pairs). Ranked measurements of correlation contribution, activity and variance contribution of individual MCs were then averaged over odor pairs (Fig. 5c). For each odor pair, pattern correlations at t₁ were dominated by high contributions from a small fraction of MCs that were also strongly active (Fig. 5c, center and left). Hence, correlated odor representations overlapped primarily in strongly responsive MCs at t₁, consistent with observations in the adult OB⁹.

We then examined the changes in the activity of individual neurons underlying the decorrelation and contrast normalization between t₁ and t₂. The activity of MCs with large r_i,t1 was significantly lower at t₂ than at t₁ (Fig. 5b,c). The mean activity of MCs that did not strongly contribute to the initial correlation, in contrast, remained similar. As a consequence, the contribution of MCs with large r_i,t1 to the overall correlation decreased, resulting in a substantial decorrelation of population activity patterns between t₁ and t₂. Pattern decorrelation can therefore be attributed, at least in part, to the selective inhibition of MC cohorts that dominated the initial pattern correlations. MCs with high r_i,t1 also made strong contributions to pattern variance at t₁ (Fig. 5c) because their activity was substantially higher than the population mean. Because the selective inhibition of these cohorts between t₁ and t₂ changed the activity of these MCs towards the population mean, the inhibition of these MCs also decreased pattern variance and its s.d. across odors. Pattern decorrelation and contrast normalization can therefore be attributed to a common mechanism that targets inhibition to specific MC cohorts and results in contrast reduction rather than contrast enhancement.

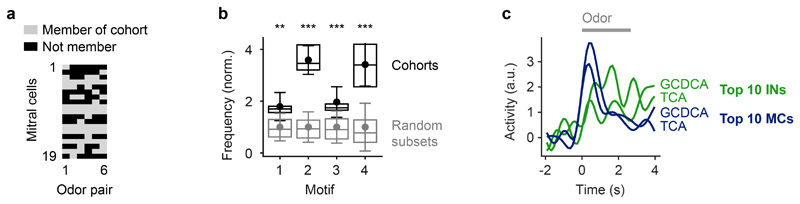
The selective suppression of activity in cohorts of co-responsive MCs cannot be achieved by global changes in subtractive or divisive inhibition because inhibition within cohorts needs to be stronger than the mean inhibition across the population in response to defined sets of odors. To explore how such stimulus- and ensemble-specific inhibition is generated by specific wiring we defined functional cohorts of MCs for each pair of bile acid stimuli as the 10 MCs with the highest r_i,t1 (Extended Data Fig. 9a). We then determined the disynaptic MC inputs to these cohorts by retrograde tracing through the wiring diagram across two synapses. Inputs to MCs within a cohort were strongly biased towards MCs of the same cohort (Fig. 5d,e). Consistent with this finding, the density of MC-IN-MC triplets, particularly motifs 2 and 4, was significantly higher within cohorts than among randomly chosen MC subsets (Extended Data Fig. 9b). Hence, cohorts of MCs are not only functional ensembles defined by similar initial responses but also anatomical ensembles with a high density of disynaptic MC-IN-MC connections.

The dense disynaptic connectivity implies that MCs in a cohort will be strongly inhibited when the cohort is activated as a whole. Indeed, the activity of MC and the associated presynaptic INs in a cohort evolved in opposite directions during an odor response (Extended Data Fig. 9c). As a consequence of cohort-specific connectivity, inhibition of MCs within a cohort will be stronger than the mean level of inhibition. The specific suppression of activity underlying whitening can thus be attributed to dense reciprocal connectivity within cohorts that are activated by specific sets of odors. Cohorts therefore function as “feature detectors”, where a “feature” is a molecular stimulus property that efficiently activates many MCs in the ensemble. When a feature is present, the activity of the corresponding MC cohort is down-regulated by feedback inhibition and the representation of the feature in population activity patterns is suppressed, which reduces correlations between related patterns. Pattern decorrelation can therefore be explained by a mechanism that involves “feature suppression” through specific connectivity. Features may correspond to functional groups that promote high correlations of afferent activity patterns because they activate overlapping sets of odorant receptors. This hypothesis predicts that MCs within functional cohorts exhibit similar input tuning to suppress the representation of such features. Indeed, the mean correlation between tuning curves of MCs at t₁ was significantly higher within cohorts (r = 0.56 ± 0.40; mean ± s.d.) than across all MCs (r = 0.01 ± 0.38; p < 10^-84; Wilcoxon rank-sum test).

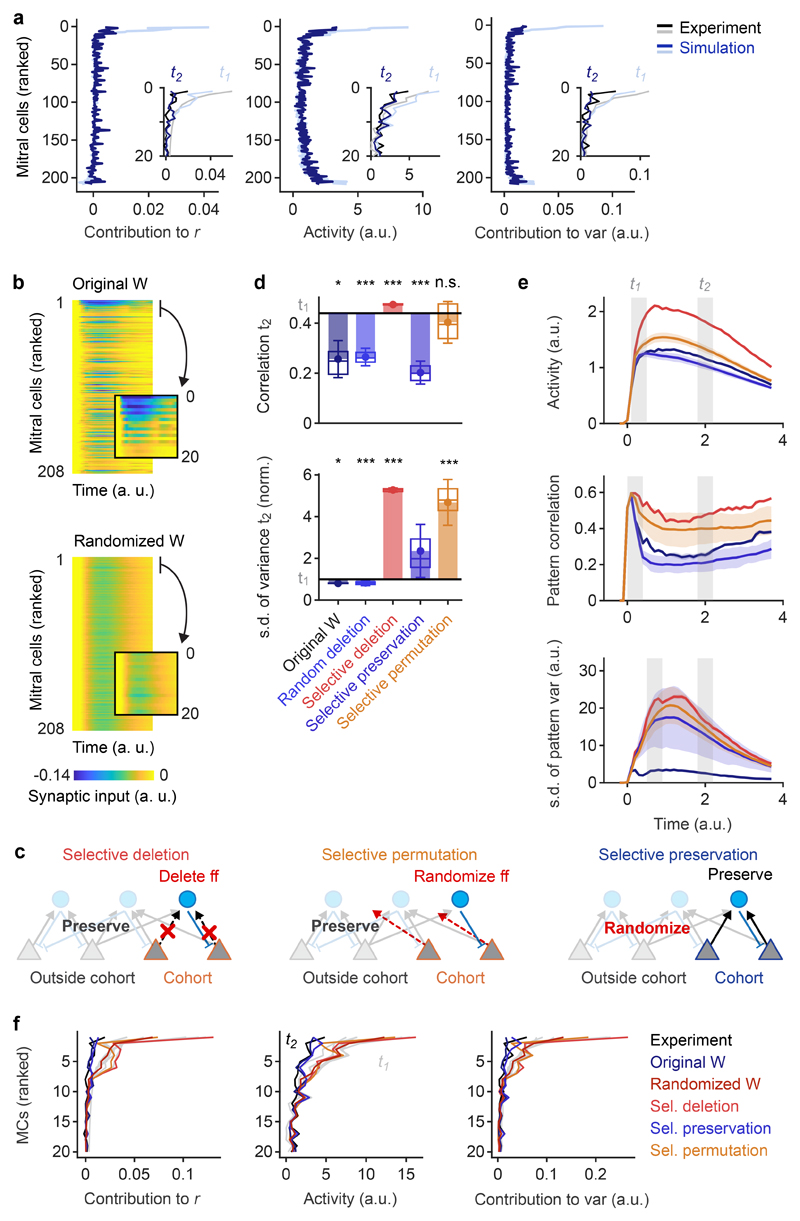
Feature suppression decreases pattern correlations by the selective inhibition of MCs with high activity and large contributions to initial correlations. To confirm that this mechanism can account for whitening in the OB we set the activity of MCs in functional cohorts (10 MCs with the highest r_i,t1 pair at t₁) to the population mean for each odor pair. As predicted, this “targeted suppression” of functional cohorts resulted in decorrelation and variance normalization (Extended Data Fig. 5b). To further dissect the mechanism of feature suppression we took advantage of simulations. We first ranked simulated MCs by their r_i,t1 for bile acid-evoked activity patterns in experiments (same ranking as in Fig. 5c). As observed experimentally, simulated MCs with large r_i,t1 were strongly inhibited between t₁ and t₂ while the mean activity of other MCs remained unchanged (Fig. 6a). Direct analysis of inhibitory inputs to individual MCs confirmed that MCs with large r_i,t1 received substantially more inhibition than other MCs. This specific targeting of inhibition to MCs with large r_i,t1 was abolished when connectivity was randomized (Fig. 6b). Simulations therefore precisely reproduced the activity changes in individual neurons that resulted in whitening, implying that simulations recapitulated the underlying mechanism. Moreover, these results further show that decorrelation and whitening of inputs cannot be achieved by global inhibition but rely on interactions among specific subsets of neurons.

Fig. 6. Mechanism of whitening analyzed by targeted manipulations of the wiring diagram.

a, Mean correlation contribution, activity, and variance contribution of MCs responding to bile acids at t₁ (light blue) and t₂ (dark blue) in simulations (correlation contribution: n = 6 bile acid pairs; activity and variance contribution: n = 8 odors). MCs were ranked by the correlation contribution r_i,t1 observed in experimental data as in Fig. 5c. Insets enlarge the top parts of the curves (20 MCs with highest r_i,t1) and compare simulation results to experimental data (gray, black) for the same 20 MCs. b, Simulated synaptic inputs as a function of time during stimulus presentation for all MCs. For each odor pair, MCs were ranked by the correlation contribution r_i,t1 in experimental data as in a and Fig. 5c. Ranked matrices were normalized and averaged over odor pairs. Inset: synaptic inputs to the 20 MCs with highest r_i,t1. Top: original wiring diagram; bottom: randomized wiring diagram. c, Schematic: selective deletion, selective permutation and selective preservation of MC cohort connectivity in simulations. d, Pattern correlation (Pearson) and s.d. of pattern variance (normalized) at t₂ observed in simulations under different conditions. Horizontal black lines show mean values at t₁. Dots show means, error bars show s.d., filled bars show difference to corresponding values at t₁, box plots show median, 25% percentile, and 75^th percentile. For simulations using the original wiring diagram, variability was determined across odor pairs (correlation; bile acids only; n = 6) or individual odors (s.d. of variance; n = 8). Significance tests compare values at t₂ to experimental values at t₁ (correlation: two-sided Wilcoxon rank-sum test; s.d. of variance: F-test with df1 = df2 = 7 degrees of freedom). For other simulation results, variability was measured across n = 50 different network simulations (repetitions). Significance tests compare repetitions to the mean value observed experimentally at t₁ (two-tailed t-test with 49 degrees of freedom). *, p < 0.05, ***, p < 0.001; n.s., not significant. P-values: correlation: 0.04, 10^-5 (t = 5.0), 10^-13 (t = 10.5), 10^-5 (t = 5.1), 0.67 (t = 0.4); s.d. of variance: 0.04 (F = 5.2), 10^-7 (t = 6.3), 10^-45 (t = 53.8), 0.07 (t = 1.84), 10^-4 (t = 4.22). e, Time courses of mean activity, mean pattern correlation (bile acid pairs) and the s.d. of pattern variance in simulations using different wiring diagrams. Shaded area shows s.d. across different permutations (n = 50). f, Mean correlation contribution, activity, and variance contribution of the 20 MCs with the highest r_i,t1 observed experimentally and in simulations using different wiring diagrams. MCs were ranked by r_i,t1 observed in experimental data as in a and in Fig. 5c (same ranking under all conditions). Gray: t₁; Colored: t₂ (mean over 50 repetitions for all permutations).

We next performed selective manipulations of the wiring diagram. We first selected the MCs with the highest r_i,t1 for each pair of bile acid stimuli (MC cohorts; 19 MCs in total; Extended Data Fig. 9a) and deleted their connections onto INs (11% of all MC→IN connections; Fig. 6c, “selective deletion”). As a control, we deleted the same fraction of feedforward connections of random subsets of MCs. While random deletions had almost no effect, the selective deletion of feed-forward connections from MC cohorts abolished pattern decorrelation and variance normalization (Fig. 6d,e). Ranking of MCs by their r_i,t1 in experimental data demonstrated that the activity of MCs with high r_i,t1 was not substantially reduced between t₁ and t₂ when MC→IN connections originating from cohorts were deleted. As a consequence, these MCs continued to make large positive contributions to pattern correlation and variance at t₂ (Fig. 6f). The selective deletion of MC→IN connections from functional cohorts therefore abolished whitening because it disrupted feature suppression. To corroborate this result we redirected feed-forward connections of MCs within cohorts to randomly selected IN targets, which perturbs the connectivity of cohorts without changing the total number of connections in the network. This manipulation (Fig. 6c “selective permutation”) also abolished whitening (Fig. 6d,e) and eliminated the specific inhibition of MCs with high r_i,t1 at t₂ (Fig. 6f), as observed for the “selective deletion” of connections.

Finally, we randomized all connections except for those between the 19 cohort MCs and their IN partners (“selective preservation”; Fig. 6c). We found that pattern decorrelation remained intact (Fig. 6d,e), contrary to the loss of decorrelation after full randomization of the wiring diagram (Fig. 3d,e). Variance normalization was partially reduced, as expected because cohorts were selected based on bile acid but not amino acid patterns. The activity of MCs with high r_i,t1 was strongly reduced at t₂ (Fig. 6f), demonstrating that pattern decorrelation and partial variance normalization were generated by feature suppression. Specific manipulations of the wiring diagram therefore demonstrate that whitening is mediated by disynaptic interactions that suppress the activity of correlation-promoting MC cohorts.

Discussion

We used a functional connectomics approach in a small vertebrate to explore the mechanism of whitening in the OB. Whitening is a computation related to object classification and associative memory that requires specific transformations of neuronal activity patterns. Such computations are thought to rely on specific wiring diagrams that are adapted to relevant inputs. Consistent with this notion, we found that whitening is achieved by specific multisynaptic interactions that cannot be described by general topographic principles or by the first-order statistics of connectivity between neuron types. Functional connectomics is therefore a promising approach to dissect distributed, memory-based computations underlying higher brain functions.

Correlations between input patterns in the OB were dominated by distinct subsets of strongly active input channels. This correlation structure is likely to reflect the co-activation of different odorant receptors by discrete functional groups^12,13 and implies that input correlations cannot be removed efficiently by contrast enhancement^35–37. Pattern decorrelation can also not be explained by the amplification of specific responses through disinhibition because it persisted when IN-IN connections were eliminated. Rather, patterns are decorrelated by the selective inhibition of strongly active, correlation-promoting MC cohorts. Pattern decorrelation is therefore achieved by a mechanism that results in contrast reduction, rather than contrast enhancement, which also supports contrast normalization.

The tuning-dependent MC-IN-MC connectivity required for whitening may be established by molecular or by activity-dependent mechanisms. We reconstructed the wiring diagram of a larva at a stage before activity-dependent effects were detected on the morphological development of glomeruli³⁸, suggesting that the initial assembly of neuronal connections may rely primarily on molecular cues. Projections of INs are enriched between glomeruli that receive input from odorant receptors of the same families²⁶, raising the possibility that glomerular targeting of sensory neurons³⁹ and INs involve related mechanisms. However, the development of specific connectivity among OB neurons remains to be explored.

Lateral inhibition between neurons with similar tuning is often assumed to sharpen tuning curves by amplifying asymmetries in the input. In the OB, however, triplet connections between related MCs are enriched in reciprocal connectivity. Such connectivity results in feedback inhibition that is independent of the precise input pattern and down-scales activity without amplifying asymmetries (Fig. 5a, right). Reciprocally connected MC↔IN↔MC cohorts therefore mediate feature suppression because the inhibitory feedback gain within the cohort is larger than the mean feedback gain when an appropriate feature is present. This mechanism can explain the selective and odor-dependent inhibition of correlation-promoting MC cohorts.

Functional connectomics permitted us to test the significance of this mechanism by implementing the wiring diagram in a network of minimally complex model neurons. Simulations included only ~30% of the MC population and did not quantitatively reproduce all details of the measured population activity. Nevertheless, the dynamics that resulted in whitening by feature suppression was preserved, demonstrating that the computational function of the circuit is determined to a large extent by its connectivity. Whitening was robust against input noise and parameter variations, presumably because the essential connectivity exhibits substantial redundancy. Precisely targeted manipulations of the wiring diagram confirmed that feedback inhibition among correlation-promoting MC cohorts was necessary and sufficient to achieve whitening. Hence, whitening in the OB depends on higher-order features of connectivity and is produced by a network mechanism that differs from canonical computations in the retina and other sensory systems, presumably because the statistical properties of sensory inputs differ between sensory modalities.

In visual cortex, functionally related principal neurons make stronger excitatory connections than random subsets of neurons⁴⁰. Such connectivity can arise from Hebbian plasticity mechanisms, enhance representations of sensory features, and amplify specific inputs in memory networks after learning. The connectivity observed in the OB, in contrast, results in disynaptic inhibitory interactions between functionally related principal neurons. Functional connectivity in the OB is therefore similar in structure, but opposite in sign, to excitatory connectivity motifs in visual cortex. As a consequence, the connectivity in the OB suppresses, rather than amplifies, specific features in the input. Such a mechanism appears useful to attenuate the impact of irrelevant sensory inputs and to reduce undesired correlations. The mechanism of feature suppression is consistent with networks that have been optimized for whitening in a theoretical framework with biologically plausible constraints^41–43, and inhibitory functional interactions between neurons with related tuning have also been observed in the rodent neocortex⁴⁴. The elementary microcircuit that mediates whitening in the OB may therefore contribute to similar computations also in other brain areas.

Methods

Animals and preparation

Adult zebrafish (Danio rerio) were maintained and bred under standard conditions at 26.5°C. Embryos and larvae of a double-transgenic line (elavl3:GCaMP5 x vglut:DsRed)^45,46 in nacre background were raised at 28.5°C in standard E3 medium⁴⁷.

Imaging experiments were performed as described previously^48,49. In brief, larvae 4 - 5 days post fertilization were contained in a small drop of aerated E3 without methylene blue or N-phenylthiourea. Larvae were then paralyzed by addition of 20 μl of fresh mivacurium chloride (Mivacron, GlaxoSmithKline, Munich, Germany)⁵⁰ and embedded in 2% low-melting agarose (type VII; Sigma, St Louis, MO, USA) in a perfusion chamber that was inclined by 30° to improve dorsal optical access to the OBs. Agarose covering the noses was carefully removed. A constant stream of E3 (2 ml/min) was delivered through a tube in front of the nose and removed by continuous suction. Throughout the experiment it was ensured that larvae showed normal heartbeat. Larvae that were not fixed for EM recovered from paralysis after a few hours and continued to develop without obvious defects. All animal procedures were performed in accordance with official animal care guidelines and approved by the Veterinary Department of the Canton of Basel-Stadt (Switzerland). The sex of zebrafish larvae is not yet determined at the age used in this study.

Odor stimulation

Odor application was performed as described⁴⁸. In brief, odors were delivered to the nose through the E3 medium using a computer-controlled, pneumatically actuated HPLC injection valve (Rheodyne, Rohnert Park, CA, USA). The rise time of stimuli was approximately 500 ms⁵¹. All experiments were carried out at room temperature (~22°C). The odor set comprised one food odor⁵¹, four bile acids (glycochenodeoxycholic acid [GCDCA], taurocholic acid [TCA], taurodeoxycholic acid [TDCA] and glycocholic acid [GCA]; Sigma Aldrich, Munich, Germany) and four amino acids (Trp, Lys, Phe, and Val; Fluka, Neu-Ulm, Germany). Stock solutions of GCDCA, TCA, TDCA, Trp, Lys, Phe and Val at 5 × 10^-3 M in E3 were kept refrigerated and diluted 1:500 (GCDCA, TCA, TDCA) or 1 : 50 (Trp, Lys, Phe, Val) in aerated E3 medium immediately before the experiment. A stock solution of GCA was prepared in 50% ethanol/50% E3 at 2.5×10^-3 M, refrigerated, and diluted 1:250 immediately before the experiment. In a given trial, an odor was applied twice for a duration of ~3 s with an inter-stimulus interval of 60 s. Successive trials with different odors were separated by at least 2 min.

Multiphoton calcium imaging

Multiphoton imaging was performed using a microscope equipped with a mode-locked Ti:sapphire laser (SpectraPhysics) and a 20× objective (NA 1.0, Zeiss) as described⁵². GCaMP5 was excited at 910 nm and emission was detected through green (535 ± 25 nm) and red (610 ± 37.5 nm) emission filters in separate channels. Images (256 × 256 pixels) were acquired at 128 ms per frame using SCANIMAGE and EPHUS software^53,54 for a total of 2 min in each trial. Trials were performed sequentially in six focal planes that were separated by approximately 10 μm along the dorso-ventral axis of the OB. The field of view covered the entire cross-section of the OB and parts of the adjacent telencephalon. Ten stimulus trials (nine odors and one E3 control), each including two odor applications, were performed in each focal plane. The order of stimuli was E3, food, GCDCA, TCA, TDCA, GCA, Trp, Lys, Phe, Val. In addition, 2 min of spontaneous activity were recorded in each focal plane. After completion of all trials a stack of images covering the whole olfactory bulb was acquired with a z-step interval of 0.5 μm.

Automated drift correction

Slow mechanical drift, which may be caused by capillary forces acting on the agarose matrix⁵⁵, was corrected between trials by an automated routine. This routine acquired a small stack (± 3 μm around the focus; 0.5 μm steps) and compared images to a reference acquired previously by cross-correlation after standardizing image columns and rows. The field of view was then automatically translated in X,Y and Z to maximize the cross-correlation to the reference.

Electron microscopy

Preparation and imaging of this sample have been described previously^25,26. Briefly, tissue was stained en bloc with osmium, uranyl acetate and lead aspartate using an established protocol^56,57 with minor modifications and embedded in Epon resin with silver particles to minimize charging^25,26. Multi-tile images were acquired in high vacuum using a scanning electron microscope (QuantaFEG 200; FEI) equipped with an automated ultramicrotome inside the vacuum chamber (3View; Gatan). Section thickness was 25 nm, pixel size was 9.25 × 9.25 nm², and the electron dose was 17.5 e^-nm^-2. The dataset comprised 4,746 successive sections of which one section was lost due to technical problems. The final stack was cropped to a size of 72.2 × 107.8 × 118.6 μm³.

Neuron reconstruction and synapse annotation

Skeletons of all neurons in the OB were reconstructed previously as described^25,26. Briefly, three independent skeletons of each neuron were generated manually from seed points at somata. Skeletons were converged and mismatches were corrected as described, and high accuracy was verified by measures of precision and recall²⁶. Tracing was performed using KNOSSOS (www.knossostool.org) or PyKNOSSOS (https://github.com/adwanner/PyKNOSSOS). Most skeletons were generated by a professional high-throughput image annotation service (www.ariadne.ai).

Synapses were annotated manually using PyKNOSSOS in “flight” mode²⁵. In the default configuration, PyKNOSSOS displays image data in four viewports: the YX viewport (imaging plane) and three mutually orthogonal viewports of arbitrary orientation. In “flight” mode, the latter is perpendicular to the direction of the current neurite. We found that this “auto-orthogonal” view increases tracing speed and facilitates the identification of branch points and synapses. Annotators followed skeletonized reference neurons along pre-calculated paths to ensure that all neurites were annotated. Most synapses were annotated by a professional image annotation service (www.ariadne.ai).

Synapses were identified by a cloud of vesicles that touched the plasma membrane, often at a site of intense staining. Annotators defined synapses by placing three nodes: (1) a node in the presynapse, (2) a node in the synaptic cleft, and (3) a node in the postsynapse. Nodes in the presynapse and postsynapse are skeleton nodes of the pre- and postsynaptic neurons if these skeletons are available. In addition, annotators assigned a confidence level c to each synapse. This confidence level was introduced because synapse identification is not unambiguous; rather, human experts can disagree whether a given structure is a synapse or not even when image quality is high.

Synapses were then classified as either “input synapse”, “output synapse”, “sensory synapse” or “unknown”. Input and output synapses are synapses of the reference neuron with the corresponding directions, excluding synapses with sensory neurons. Sensory synapses are input synapses received by the reference neuron from axons of sensory neurons, which were identified by their dark cytoplasm⁵⁸. Unknown structures resemble synapses but do not display all characteristic features. These structures often included an intense staining of the membrane but no clearly associated vesicle cloud. We therefore speculate that some of these structures may be gap junctions.

We first annotated input and output synapses of all MCs and INs independently of each other. Hence, each synapse should have been encountered twice, once from the presynaptic side and once from the postsynaptic side. Synapses of INs were then annotated again by different individuals, resulting in a 3-fold redundancy for each MC-IN synapse. In order to minimize the number of false positives the final wiring diagram retained only those MC-IN synapses that were annotated on the MC and at least once on the IN. As a control, we also repeated connectivity analyses and simulations with a wiring diagram that included only those synapses that were annotated at least three times. This wiring diagram produced very similar results (not shown).

Each synapse was assigned a unitary weight. As a consequence, the strength of the connection between two neurons in each direction was given by the number of synapses between this pair of neurons. In addition, we tested two other methods to determine synaptic strength. First, connection strength was binarized such that all connections had strengths 0 or 1, independent of the number of synapses. Second, we defined the weight of a synapse as its mean confidence level c, and the total weight of a connection as the sum of the confidence levels of all synapses. In addition, we tested various confidence thresholds to discard synapses with low confidence before determining the weights. Similar results were obtained with all methods and a wide range of confidence thresholds, implying that results are highly robust.

Correlation between multiphoton and SBEM image stacks

Mapping of multiphoton to SBEM image data may be complicated by (1) mechanical distortions introduced by the sample preparation procedure, (2) shrinkage due to loss of extracellular space induced by chemical fixation⁵⁹, and (3) developmental changes occurring during the approximately three hours between the first calcium imaging trial and the final fixation of the tissue. Initial observations indicated that distortions between image datasets were mostly linear (rotation, translation, shrinkage) while non-linear distortions appeared minimal and developmental changes were negligible. We therefore used an affine transformation to map multiphoton images into the SBEM stack, followed by manual fine adjustment of regions of interest (ROIs) for the extraction of calcium signals.

An initial affine transformation matrix was fitted to a set of corresponding points that were selected manually in both datasets. The EM volume was then transformed onto the two-photon images, the position of existing points were optimized manually, and additional pairs of corresponding points were selected. The transform was then re-calculated based on the updated set of landmarks and this procedure was iterated until asymptotic behavior was observed.

All somata of the OB were outlined manually in the SBEM dataset and mapped onto the time-averaged multiphoton fluorescence images of each trial, resulting in 7280 mappings of somatic outlines in the SBEM dataset to regions of interest (ROIs) in 66 multiphoton images (11 trials at each of six optical planes). The position of all ROIs was then manually adjusted to optimize the mapping in each trial. The average displacement of ROIs during manual adjustment was small (593 ± 833 nm; mean ± s.d.; Extended Data Fig. 1b), demonstrating that the accuracy of the initial affine mapping was already high.

INs in the larval zebrafish OB were previously divided into three classes based on morphological criteria²⁶. The 68 INs included in the activity dataset included neurons from all three without an obvious bias (13/53 INs of class 1, 20/78 INs of class 2, 31/123 INs of class 3). Moreover, they included 4/4 neurons that were previously classified as atypical projection neurons²⁶. We did not observe an obvious bias of IN classes for specific connectivity motifs.

Analysis of calcium signals

Individual frames of multiphoton image time series were low-pass spatially filtered with a mild 2D Gaussian kernel (σ = 1.2 pixels). Baseline fluorescence F was calculated as the average fluorescence during a 2 s window before response onset. Traces representing relative changes in fluorescence (ΔF/F) in each ROI were averaged over the two successive odor applications in each trial and band-pass filtered in time using a Butterworth filter with a cutoff frequency of 0.2 times the frame rate. The average population response onset (t = 0) was determined manually from all raw ΔF/F traces and fixed for all trials. Firing rate changes of neurons represented by individual ROIs were estimated by temporal deconvolution of calcium signals as described²⁸ using standard parameters (τ_decay = 3 s, thr_noise = 0).

Analyses of population activity were restricted to neurons represented by ROIs with a radius ≥2 pixels in all trials (corresponding to an area of 3.14 μm²; 232 MCs and 68 INs). For network simulations and mechanistic analyses of whitening we considered only the 208 MCs that were pre- and post-synaptic to at least one IN and excluded 24 presumably premature MCs. Population responses to different odors were compared by calculating the Pearson correlation coefficient between the population activity vectors of MCs for the different stimuli at a given time point after response onset.

Network modeling

MCs are glutamatergic while most or all INs in the developing zebrafish OB express GABA⁴⁸. We therefore consider MCs to be excitatory and INs to be inhibitory. MCs and INs were simulated as threshold-linear units with a state variable representing firing rate. The rⁱ(t) and u^j(t) representing firing rates of MC i and IN j, respectively, followed the equations of motion

$${\tau }_{MC}^i\cdot \frac{d{r}^i(t)}{dt}=-r^i(t)+G_{sen}^i{S}^i(t)-G_{inh}^i{W}_{MC\leftarrow IN}^i\cdot {[\overrightarrow{u}(t)-{\overrightarrow{\theta }}_{IN}]}_{+}$$

$${\tau }_{IN}^j\cdot \frac{d{u}^j(t)}{dt}=-u^j(t)+G_{exc}^j{W}_{IN\leftarrow MC}^j\cdot {[\overrightarrow{r}(t)-{\overrightarrow{\theta }}_{MC}]}_{+}$$

where the vectors ${\overrightarrow{\theta }}_{MC}$ and ${\overrightarrow{\theta }}_{IN}$ are firing thresholds, $W_{IN\leftarrow MC}^j$ and $W_{MC\leftarrow IN}^i$ correspond to the reconstructed IN-to-MC and MC-to-IN connectivity weight matrices of the j^th IN and of the i^th MC, respectively, and the vectors $\overrightarrow{r}(t)$ and $\overrightarrow{u}(t)$ represent the firing rates of the MC and IN, respectively. []₊ denotes half-wave rectification:

$${[x(t)]}_{+}=\{\begin{array}{rr}\hfill 0,& \hfill x(t)<0\\ \hfill x(t),& \hfill x(t)\ge 0\end{array}$$

${\tau }_{MC}^i$ and ${\tau }_{IN}^j$ are the time constants for the individual MCs and INs, respectively. $G_{sen}^i,$ $G_{inh}^i$ and $G_{exc}^j$ are the individual scaling factor for sensory, inhibitory and excitatory input, respectively. To account for the natural variability in biological systems, the parameter values for each of the cells in each of the individual simulation runs were drawn from a Gaussian distribution with a standard deviation of 1% of the distribution mean. The distribution means of the different parameters were:

G_sen = 6, G_exc = 0.7, G_inh = 3.5, θ_MC = 2, θ_IN = 50, τ_MC = 1, τ_IN = 80;

The time course of sensory input Sⁱ(t) was modelled as difference of exponentials as described previously³³:

$$\tilde{\text{s}}(t)=-a_{j,\infty }+\frac{a_{j,\infty }}{1-\alpha }(1-e^{-{\tau }_{r}t}-\alpha +\alpha e^{-{\tau }_{d}t})\text{with}\alpha =0.8,{\tau }_r=\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$150$}\right.,{\tau }_d=\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$600$}\right.,a_{j,\infty }=\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$150$}\right.$$

To model S_i(t), the individual sensory input of MC i, we used its experimentally measured activity ${\widehat{a}}_i$ during t₁ and modulated the time course according to $\tilde{s}(t)$:

$$S_i(t)={\widehat{a}}_i\frac{\tilde{\text{s}}(t)}{{\tilde{s}}_{max}},\text{where}{\tilde{s}}_{max}=\underset{t\ge 0}{max}(\tilde{\text{s}}(t))$$

The differential equations were solved in MATLAB with a fixed step size of 1 millisecond using a first degree Newton-Cotes integration scheme or using an adaptive step size embedded Runge-Kutta-Fehlberg (4, 5) scheme. Both integration schemes lead to qualitatively very similar results, and therefore the former method was used for simplicity for the simulated data shown here.

In an iterative, semi-automated parameter search, we identified a suitable parameter range that fulfilled the following criteria:

• (1)The peak firing rates of individual neurons does not exceed a physiologically realistic range (< 200 Hz).
• (2)The strength of inhibition is appropriate to reproduce the time course of the average population activity, correlation and variance.
• (3)The activity, correlation contribution and variance contribution of individual MCs at t₁ and t₂ is in good correspondence to experimental measurements.

Parameters for which these criteria were fulfilled were found by parameter variations in pilot studies. Results were usually robust against variations of each parameter by ±50% around the values reported above.

To simulate responses to noisy inputs we assumed that a MC receives convergent input from 40 olfactory sensory neurons of the same type, each spiking with Poisson statistics. Simulated firing rates of sensory neurons were calculated in 25 ms windows, averaged over convergent sensory neurons, and scaled to obtain a total input to each MC with the same mean as in the noiseless case. Assuming that each sensory neuron makes 10 synapses onto MCs, the total number of sensory neurons would be approximately 3’000 per epithelium.

Analysis of triplet motifs

Occurrences of disynaptic MC-IN-MC and IN-MC-IN motifs were counted after binarizing connections. We enumerated all neuron triplet combinations in the reconstructed wiring diagram and tested for graph isomorphism against all 4 disynaptic motif types. The obtained motif counts were compared against a reference model where the forward and backward connectivity of the MCs were permuted independently while maintaining the node count and edge density (n = 10,000 permutations). The z-scores and p-values were obtained by computing the mean and standard deviation of each motif type in the permuted networks.

To compare the motif frequency as a function of the pairwise tuning similarity, we divided the MC pairs into two groups, one with tuning correlation higher than a threshold (e.g., r > 0.5) and one with tuning correlation lower than the threshold (r ≤ 0.5), and counted the occurrences of MC-IN-MC and IN-MC-IN motifs in each group. We then compared the motif counts against a reference model where we permuted the pairwise tuning similarity between MCs and regrouped them by tuning correlation while maintaining the same network topology (n = 10,000 permutations). The z-scores and p-values were then obtained by computing the mean and standard deviation of each motif type in the permuted groups.

Additional analyses

The contribution of individual MCs to the Pearson correlation coefficient

$$r=\frac{1}{n-1}{\displaystyle \sum _{i=1}^n\left(\frac{x_i-\overline{x}}{s{d}_x}\right)}\left(\frac{y_i-\overline{y}}{s{d}_y}\right)$$

between population activity patterns was calculated by determining the summand $\left(\frac{x_i-\overline{x}}{s{d}_x}\right)\left(\frac{y_i-\overline{y}}{s{d}_y}\right)$ for each MC. Similarly, the contribution of individual MCs to the variance

$$s{d}_x^2=\frac{1}{n-1}{\displaystyle \sum _{i=1}^n{(x_i-\overline{x})}^2}$$

of the population activity patterns was calculated by determining the summand ${(x_i-\overline{x})}^2$ for each MC. Here, x_i and y_i are responses of MCs to odors x and y, sd_x and sd_y are the standard deviations of population responses to odors x and y, and n is the total number of MCs in the population.

The analysis of disynaptic connectivity as a function of tuning correlation (Fig. 4c; Extended Data Fig. 7c) included only neurons that showed an obvious response because correlation measurements are sensitive to noise. A neuron was classified as responsive when the average of the two largest responses exceeded the mean across all neuron-odor pairs by 0.6 standard deviations. When applied to the matrix representing all MCs and odors, approximately 30% of MCs were classified as responsive by this criterion. Weights of input synapses were normalized for each neuron to the sum of all inputs to that neuron and final plots were normalized to the mean.

Statistical analysis

No statistical methods were used to pre-determine sample sizes but our sample sizes are similar to those reported in previous publications^8,10,14,15 or larger. Reconstruction of the wiring diagram required no sampling because all neurons and synapses were annotated. Neurons were randomly assigned to annotators for reconstruction. The study included only one animal. Stimulus presentation was not randomized. Annotators were blind to the identity of neurons. Otherwise, data collection and analysis were not performed blind to the conditions of the experiments. No animals or datapoints were excluded from analyses. Statistical comparisons were performed using a two-sided Wilcoxon rank-sum test, a two-tailed t-test, a permutation test, or an F-test. Normality and equal variance were tested when statistical tests were used that make these assumptions.

Extended Data

Extended Data Fig. 1. Sensory input to INs and mapping of datasets.

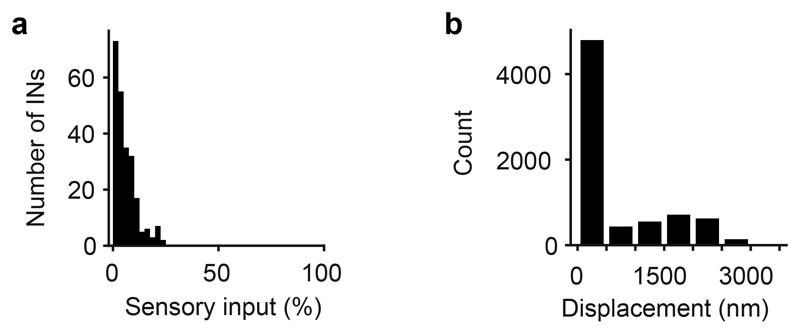
a, Distribution of the fraction of synaptic inputs onto INs that originated from sensory axons. The average fraction of synaptic inputs onto INs that came from sensory neurons was 5.9 ± 4.6% (mean ± s.d.). This is an upper-bound estimate because structures in EM images were classified as sensory synapses even when they were small and when synaptic features such as postsynaptic densities and vesicle clusters were ambiguous. No obvious synaptic connections were observed from OB neurons onto axon terminals of sensory neurons. b, Displacement of regions of interest (ROIs) during manual proofreading. ROIs representing somata were mapped from the EM dataset to optical image planes in each trial by an affine transformation that was determined by an iterative landmark-based procedure (Methods). Subsequently, the position of each ROI was adjusted manually on the optical image (n = 7,280 ROIs; six image planes with 11 trials each). The mean displacement (± s.d.) during manual adjustment (proofreading) was small (593 ± 833 nm), implying that automated mapping was highly reliable.

Extended Data Fig. 2. Calcium imaging of odor responses.

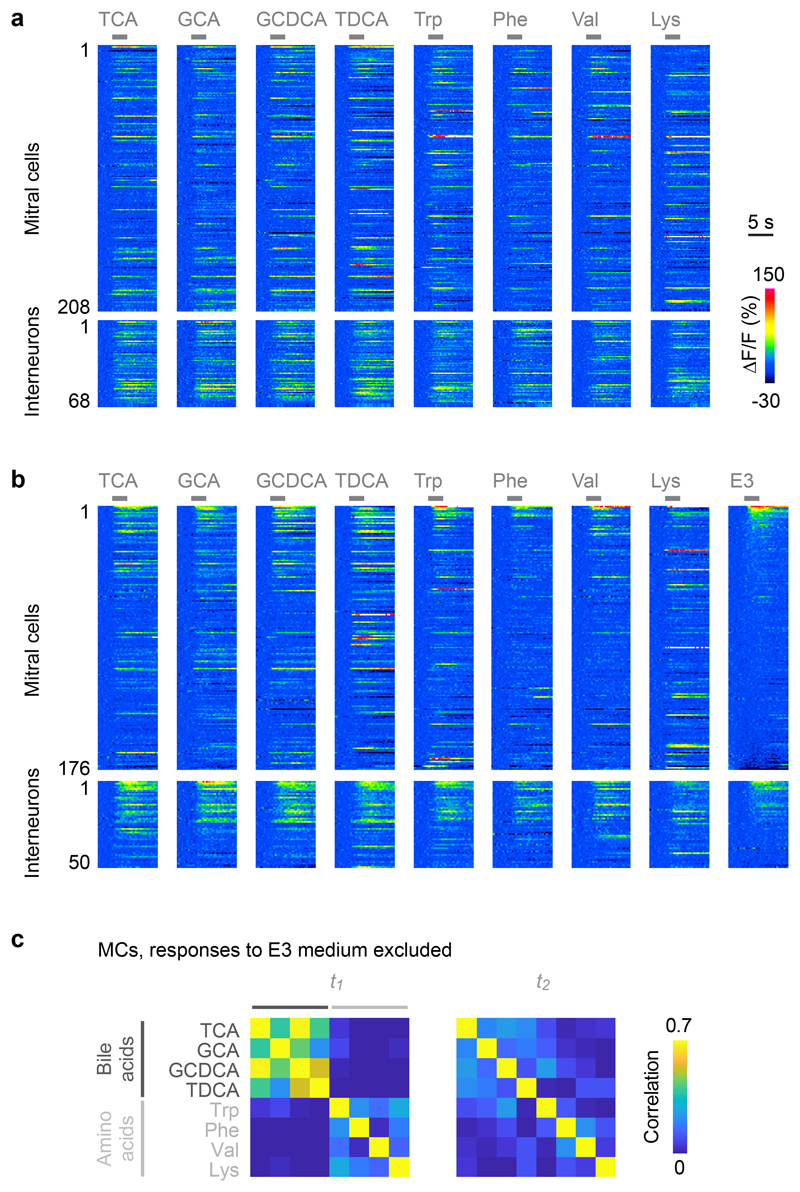
a, Raw calcium signals (ΔF/F) evoked by eight odors in neurons that were present in all trials and included in simulations (208 MCs and 68 INs; average of two trials). Gray bars indicate odor stimulation. b, Raw calcium signals (ΔF/F) evoked by eight odors and E3 medium in neurons that were present in all trials and included in simulations (176 MCs and 50 INs; average of two trials; sorted by response to E3 medium). c, Correlation matrices of MC activity patterns at t₁ and t₂ after excluding 10 MCs with highest responses to E3 medium (all MCs in b except for the first 10; n = 166 MCs in total). Calcium signals were deconvolved to estimate firing rate changes as in Fig. 2. As observed in the full dataset (Fig. 2e), MC activity patterns evoked by similar odors were correlated at t₁ and became decorrelated at t₂. The main results were therefore not affected by possible responses to E3 medium.

Extended Data Fig. 3. Decoding of odor identity from MC activity patterns.

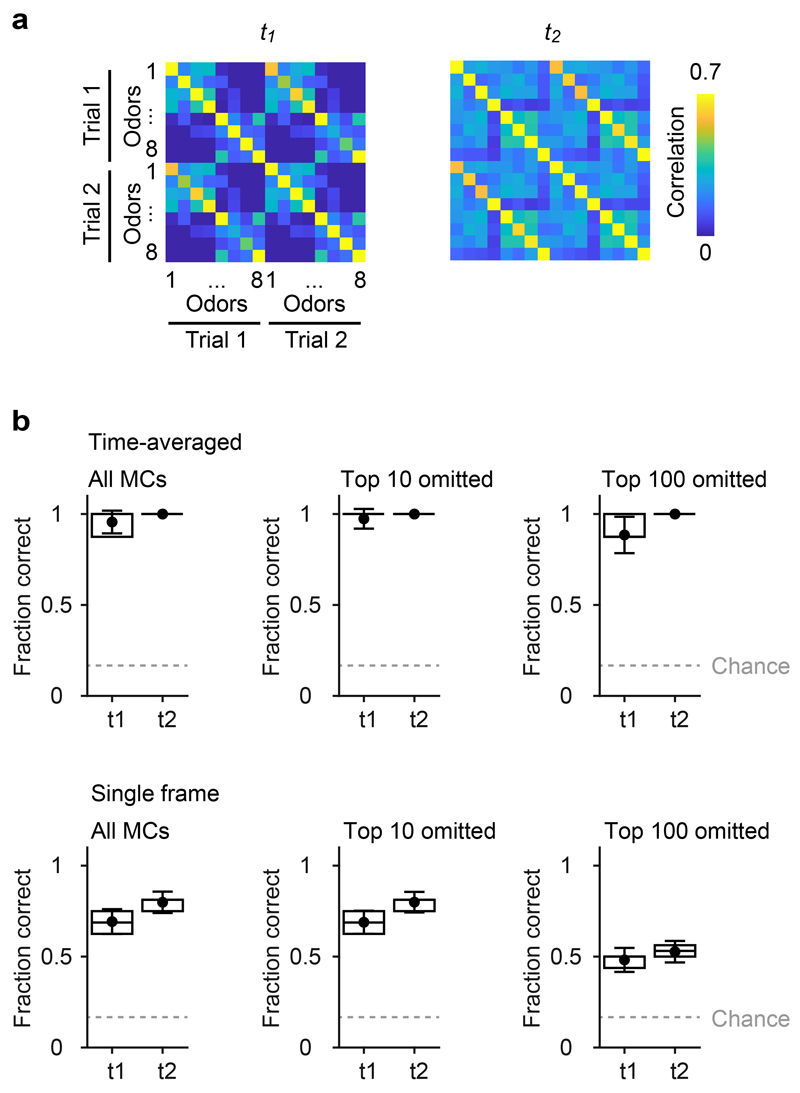
a, Pearson correlation matrices showing similarities of activity patterns across odors and trials at t₁ and t₂ (average over 100 repetitions). In each repetition, two activity patterns (trials) were generated for each odor by randomly assigning the first or second response of each neuron to each trial. Note the high correlations between activity patterns representing the same odor in different trials, particularly at t₂. b, Success rates of odor identification by template matching. For each odor, the vector representing the odor in one trial (test vector) was correlated to vectors representing all odors in the other trial (templates) and assigned to the odor represented by the template with the highest correlation. Dots show the mean fraction of correct identifications, error bars show s.d., boxes show median, 25^th percentile and 75^th percentile (n = 100 repetitions each). Dashed gray line shows chance level. Top: identification based on patterns averaged over time windows t₁ and t₂ (see text). Bottom: identification based on single frames within t₁ and t₂. Left: tests and templates included all MCs. Center, right: the 10 or 100 MCs with the highest contribution to the initial pattern correlation (highest r_i,t1) were omitted for each odor pair. Omitting the 10 MCs with the highest r_i,t1 (cohorts) had almost no consequence on odor identification, confirming that information about precise odor identity is conveyed predominantly by other MCs.

Extended Data Fig. 4. Additional simulation results.

a, Mean Pearson correlation between IN activity patterns (blue) and the corresponding MC activity patterns (black) evoked by different bile acid inputs in simulations (n = 6 bile acid pairs each). Correlations between IN activity patterns remain higher than correlations between MC activity patterns. b, Mean Pearson correlation between simulated MC activity patterns evoked by inputs representing different odors (blue; all bile acid pairs) and between activity patterns evoked by inputs representing the same odors in trials with input noise (purple; all bile acids). Shading shows s.d.. Noise was modeled based on conservative estimates of the number and firing rates of olfactory sensory neurons in zebrafish larvae (Methods). Three noisy trials were simulated for each odor, resulting in n = 12 correlations between same-odor trials and n = 54 correlations between different-odor trials. Patterns evoked by different inputs were decorrelated whereas noisy versions of the same inputs were not decorrelated.

Extended Data Fig. 5. Algebraic transformations of sensory inputs.

a, Schematic: simple algebraic approach to approximate transformations of MC activity patterns by feedback inhibition. Input activity patterns (MC activity at t₁) were multiplied by the feed-forward connectivity matrix W_MC→IN, normalized and thresholded. Normalization and thresholding are basic operations performed by the neuronal circuits of the OB¹⁰ and by individual neurons, respectively. The resulting IN activity patterns were multiplied with the feedback connectivity matrix W_MC←IN, resulting in odor-specific patterns of feedback inhibition onto MCs. Feedback inhibition was either subtracted from the MC activation patterns (subtractive inhibition), or MC activation patterns were divided by the feedback inhibition patterns (divisive inhibition), followed by thresholding. Scaling factors and thresholds were adjusted so that effects on the mean activity were small. b, Mean activity, Pearson pattern correlation and s.d. of pattern variance at t₂ after algebraic transformations of input patterns as described in a (“Experiment”: experimental results). Horizontal black lines show mean experimental values at t₁; activity and s.d. of pattern variance is normalized to the experimental value at t₁. Dots show means, error bars show s.d., filled bars show difference to corresponding values at t₁. Box plots show median, 25% percentile, and 75^th percentile. For experimental results and simulations using the reconstructed wiring diagram, variability was measured across odor pairs (correlation; bile acids only; n = 6) or individual odors (s.d. of variance; n = 8). Significance tests compare values at t₂ to experimental values at t₁ (correlation: two-sided Wilcoxon rank-sum test; s.d. of variance: F-test with df1 = df2 = 7 degrees of freedom). For results obtained with randomized wiring diagrams (W random), variability was measured across n = 50 permutations of the wiring diagram. Significance tests compare repetitions to the mean value observed experimentally at t₁ (two-sided Wilcoxon rank-sum test). *, p < 0.05; **, p < 0.01; ***, p < 0.001; n.s., not significant. In “targeted suppression”, the activity of the 10 MCs that contributed most strongly to the pattern correlation at t₁ for each odor pair (“functional cohort”) was set to the population mean. No other manipulations or algebraic operations were performed. P-values: activity: 0.57, 0.57, 0.25, 0.23 0.17; Pearson correlation: 0.03, 0.04, 0.98, 0.04, 0.008; s.d. of variance: 0.003, 10^-23, 10^-26, 10^-21, 10^-16.

Extended Data Fig. 6. Occurrence of connectivity motifs as a function of tuning correlation.

Z-scores quantify the over-representation of motifs among MC pairs with signal correlations greater than a threshold between -0.8 and 0.8. For each motif, color-coded bars show z-scores for different signal correlation thresholds. Z-scores were determined by comparison against 10,000 shufflings of the tuning correlation matrix as in Fig. 4d.

Extended Data Fig. 7. Functional connectivity between interneurons.

a, IN-MC-IN triplets included in the analysis. Connections between INs were analyzed separately (see below and main text) to facilitate the comparison to MC-IN-MC triplets (Fig. 4). b, Left: number of IN-MC-IN motifs found in the wiring diagram (considering only INs with activity measurements and at least one MC→IN and MC←IN connection; n = 66). Right: z-score quantifying over- or under-representation of motifs as compared to 10,000 independent randomizations. c, Top: disynaptic connections between responsive INs as a function of tuning similarity (Pearson correlation), normalized to the mean (n = 992 neuron pairs; neurons were included only when their activity exceeded a threshold; see Methods; number of neuron pairs per bin: 192, 218, 178, 228, 176). Dots and error bars show mean ± s.e.m. when tuning curves were determined using all eight odor stimuli. Box plots show median, 25^th percentile and 75^th percentile across results when tuning curves were determined by all possible combinations of four odors. Bottom: result of the same analysis including only reciprocal connections (motif 4; n = 992 neuron pairs). d, Left: Pearson correlations between the mean tuning curves of MC inputs to INs (n = 57 INs). INs were ordered by optimal leaf ordering for hierarchical clustering. Right: Pearson correlations between the mean tuning curves of the MC targets of INs (same ordering of INs). INs were included in the analysis when their activity was measured, when they received input from at least 1 MC and 1 IN for which activity measurements were available, and when they targeted at least 1 MC and 1 IN for which activity measurements were available. e, X-axis: Pearson correlation between the tuning curves of each IN and the mean tuning curves of MC inputs to the same IN (r_IN-inputs). Y-axis: Pearson correlation between the tuning curves of each IN and the mean tuning curves of its MC targets (r_IN-targets). r, correlation coefficient; ***, p = 10^-8 (two-tailed t-test, n = 63 INs). INs were included in the analysis when their activity was measured, when they received input from at least 1 MC for which activity measurements were available, and when they targeted at least 1 MC for which activity measurements were available. f, Black: number of maximal IN cliques in the wiring diagram as a function of clique size. Gray curve shows expectation based on randomized wiring diagrams (10,000 permutations). A maximal clique is a complete set of INs that are all reciprocally connected to each other. Top and bottom plots show distributions for cliques without a MC and cliques with one reciprocally connected MC, respectively. Maximal cliques with more than one MC do not exist because the wiring diagram contained no connections between MCs. g, Left: Mean Pearson correlation of tuning curves between neurons in maximal cliques as a function of clique size (n = 414; number per bin: 3, 19, 22, 44, 96, 99, 75, 29, 24, 3). Dots and error bars show mean ± s.e.m.; box plots show median, 25^th percentile and 75^th percentile. Gray curve shows mean after shuffling of tuning correlation matrix (right). Right: same analysis after shuffling of tuning correlation matrix (1,000 repetitions; n = 414,000; number per bin: 3,000, 19,000, 22,000, 44,000, 96,000, 99,000, 75,000, 29,000, 24,000, 3,000). Black curve shows mean of original data (left).

Extended Data Fig. 8. Effects of different transformations on pattern correlation.

a, Schematic: effect of contrast enhancement on the correlation between displaced Gaussian patterns. The X-axis represents neurons while the Y-axis represents their activity. Blue and orange bars represent overlapping activity patterns evoked by two different stimuli. The similarity of activity patterns is quantified by the Pearson correlation coefficient, r. Note that many neurons respond to both stimuli but neurons showing maximal responses differ between stimuli. Hence, strongly active neurons convey stimulus-specific information. Contrast enhancement therefore decorrelates patterns because it emphasizes strongly active neurons and suppresses weakly active neurons. b, Effect of contrast enhancement on the Pearson correlation between activity pattern that overlap in strongly active neurons. Activity patterns have the same Pearson correlation as in a but their shape is slightly different: maximal responses to the two stimuli occur in the same neuron, and tails of moderately or weakly active neurons extend in opposite directions. Hence, stimulus-specific information is conveyed primarily by moderately or weakly active neurons while strong responses are non-specific. As a consequence, contrast enhancement fails to decorrelate these patterns. c, Patterns that overlap in strongly active neurons (same as in b; r: Pearson correlation) are decorrelated by selective inhibition of strongly active neurons, which results in contrast reduction. Decorrelation occurs because the relative contribution of moderately or weakly active neurons is enhanced as the activity of strongly active neurons is suppressed. Selective inhibition of strongly active units is generated by reciprocal inhibition that is stronger or denser within cohorts of co-tuned neurons. Inhibitory feedback gain is therefore higher than the average inhibitory feedback gain within a co-tuned cohort when the stimulus feature that activates the cohort is present (feature suppression).

Extended Data Fig. 9. Further characterization of functional cohorts.

a, Composition of functional MC cohorts. For each pair of bile acid odors (X-axis), a functional MC cohort was defined as the 10 MCs that contribute most to the correlation between odor-evoked activity patterns at t₁ (highest r_i,t1). Gray pixels denote membership of each MC (Y-axis) in each cohort. Cohorts for different odor pairs overlapped substantially. Consistent with this observation, the mean Pearson correlation between tuning curves of MCs at t₁ was significantly higher within cohorts (r = 0.56 ± 0.40; mean ± s.d.) than across all MCs (r = 0.01 ± 0.38; p = 10^-84; two-sided Wilcoxon rank-sum test). Furthermore, we analyzed the mean tuning correlation at t₁ among the 16 MCs that were not part of cohorts themselves but provided the highest number of disynaptic input connections to neurons inside cohorts (r = 0.23 ± 0.52; mean ± s.d.). This tuning correlation was lower than the tuning correlation within the cohort but still significantly higher than the mean tuning correlation across all MCs (p = 10^-40; two-sided Wilcoxon rank-sum test). Similarly, the mean tuning correlation at t₁ among the 16 MCs that received the most disynaptic output connections from neurons inside cohorts (r = 0.17 ± 0.53; mean ± s.d.) was lower than the tuning correlation within the cohort but significantly higher than the mean tuning correlation across all MCs (p = 10^-17; two-sided Wilcoxon rank-sum test). b, Black: frequency of each MC-IN-MC triplet motif in MC cohorts (n = 6 cohorts for each motif). Dots show means, error bars show s.d., box plots show median, 25% percentile, and 75^th percentile. Gray: frequency of MC-IN-MC triplet motifs among randomly selected MC subsets of the same size (n = 10 MCs; n = 600 repetitions for each motif). Frequency of occurrence is normalized to the mean frequency in random subsets for each motif. **, p < 0.01; ***, p < 0.001 (two-sided Wilcoxon rank-sum test). P-values: 0.002, 10^-5, 0.0008, 0.0001. We also observed that the 10 INs receiving the largest number of MC inputs from each cohort were 1.7 times more likely to make direct connections than random subsets of INs (p = 0.007; two-sided Wilcoxon rank-sum test). c, Blue: mean activity of the 10 MCs in the functional cohort defined by responses to TCA and GCDCA (example odors in Fig. 5b). Green: mean activity of the 10 INs that were included in activity measurements and provided the highest synaptic input to the MC cohort. As expected, IN activity increased while MC activity decreased during odor application.