Fig. 2. Second-order response by skew scattering on a honeycomb lattice.

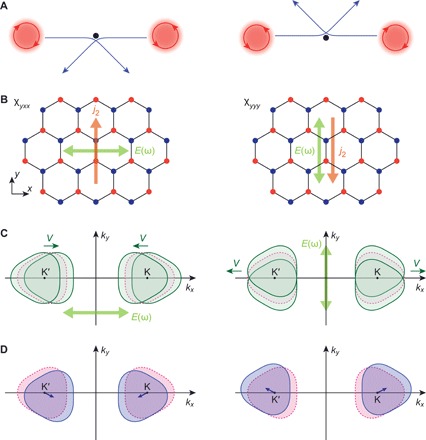
(A) Schematics of skew scattering. When a self-rotating wave packet (red) is scattered by an inversion-symmetric potential (black), its motion is deflected like the Magnus effect. Two wave packets moving in the opposite directions produces zero net current. However, if the two self-rotate in different directions, then skew scattering produces net current in the perpendicular direction. (B) Electric field and rectified current on a honeycomb lattice. The left and right panels in (A) to (D) correspond to χ_yxx and χ_yyy, respectively. (C) Fermi surface displacement at frequency ω (green). The oscillating electric field E(ω) forces the Fermi surface to swing back and forth from its equilibrium position (red). Owing to the Fermi surface anisotropy, each valley yields finite velocity V along the k_x direction after time averaging. This velocity is canceled with the two valleys, and there is no DC current generated as a linear response. (D) Stationary Fermi surface displacement. The electric field and skew scattering produce the stationary Fermi surface displacement (blue) from the equilibrium state (red) as a second-order response. Finite rectified current is observed when the contributions from the two valleys do not cancel.