High-gradient diffusion MRI reveals distinct estimates of axon diameter index within different white matter tracts in the in vivo human brain

Abstract

Axon diameter and density are important microstructural metrics that offer valuable insight into the structural organization of white matter throughout the human brain. We report the systematic acquisition and analysis of a comprehensive diffusion MRI dataset acquired with 300 mT/m maximum gradient strength in a cohort of 20 healthy human subjects that yields distinct and consistent patterns of axon diameter index in white matter tracts of arbitrary orientation. We use a straightforward, previously validated approach to estimating indices of axon diameter and volume fraction that involves interpolating the diffusion signal perpendicular to the principal fiber orientation and fitting a three-compartment model of intra-axonal, extra-axonal and free water diffusion. The resultant maps confirm the presence of larger diameter indices in the body of corpus callosum compared to the genu and splenium, as previously reported, and show larger axon diameter index in the corticospinal tracts compared to adjacent white matter tracts such as the cingulum. An anterior-to-posterior gradient in axon diameter index is also observed, with smaller diameter indices in the frontal lobes and larger diameter indices in the parieto-occipital white matter. These observations are consistent with known trends from prior histologic studies in humans and non-human primates. Rather than serving as fully quantitative measures of axon diameter and density, our results may be considered as axon diameter- and volume fraction-weighted images that appear to be modulated by the underlying microstructure and may capture broad trends in axonal size and packing density, acknowledging that the precise origin of such modulation requires further investigation that will be facilitated by the availability of high gradient strengths for in vivo human imaging.

Introduction

Axon diameter is a key microstructural metric that reflects differences in white matter structure and function throughout the central nervous system. Variations in axon diameter are thought to be closely tied to function, with networks that demand fast response times such as motor networks demonstrating larger diameter axons. Studies in non-human primates using tracer injections have revealed that axons arising from different cortical regions vary in diameter, with the thickest axons originating from primary motor and primary somatosensory cortex and the thinnest axons residing in the prefrontal and temporal regions (Innocenti et al. 2014; Tomasi et al. 2012). A robust, noninvasive method for probing indices of axon diameter in the living human brain would provide invaluable information regarding structural connectivity and dynamics between different cortical regions and enable the study of structural plasticity and alterations in white matter microstructure in normal aging as well as a number of neurological and psychiatric conditions.

Diffusion MRI has been proposed as a noninvasive method for probing axonal diameter and density (Alexander et al. 2010; Assaf and Basser 2005; Assaf et al. 2008; Assaf et al. 2004; Barazany et al. 2009; Ong and Wehrli 2010; Stanisz et al. 1997; Zhang et al. 2012). Robust methods for in vivo mapping of tissue microstructure by diffusion MRI require fast and strong diffusion-encoding gradients (Dyrby et al. 2013; Huang et al. 2015a; Nilsson et al. 2017), which are not accessible on clinical MRI scanners, where the maximum gradient strength is typically on the order of 40–80 mT/m. Therefore, such studies have been largely limited to ex vivo samples and/or animal models on small-bore MRI systems to date. The advent of higher maximum gradient strengths on human MRI scanners (Setsompop et al. 2013) has enabled the translation of axon diameter mapping to study white matter tracts more precisely in the in vivo human brain. These studies have primarily focused on the structure of the corpus callosum in a few healthy subjects (Huang et al. 2015a; Huang et al. 2015b; McNab et al. 2013) and patients with multiple sclerosis (Huang et al. 2016).

The goal of this study is to demonstrate the consistency of axon diameter indices obtained in the in vivo whole human brain in a moderate-sized cohort of healthy human subjects and to provide a benchmark dataset against which future modeling approaches can be assessed. To achieve this goal, we use a straightforward approach to estimate the axon diameter index and volume fraction in fiber tracts of arbitrary orientation that has recently been validated in a biomimetic brain phantom (Fan et al. 2018) and apply this analysis to high-quality whole brain diffusion MRI data acquired using a comprehensive imaging protocol with 300 mT/m maximum gradient strength in 20 healthy subjects. Our analysis involves interpolating the signal perpendicular to the principal fiber orientation and fitting for the axon diameter index and volume fraction using a model of intra-axonal, extra-axonal and free water diffusion. It is important to note that our method provides axon diameter- and volume fraction-weighted estimates of relative axonal size and packing density within the limits of the high-gradient diffusion MRI acquisition and modeling, rather than serving as strict quantitative measures of axon diameter and density. We evaluate the consistency of axon diameter index and volume fraction estimates obtained in vivo within and between subjects using a comprehensive acquisition performed with state-of-the-art hardware and imaging protocols and explore the differences in axon diameter index along specific tracts, including the corticospinal tracts and adjacent white matter tracts.

Methods and Materials

Data Acquisition

With approval from the institutional review board, 20 healthy volunteers (mean age 33.8±11.4 years, 7 male and 13 female) were scanned. Informed consent was obtained from all individual participants included in the study. All scans were performed on a dedicated high-gradient 3T MRI scanner (MAGNETOM CONNECTOM, Siemens Healthcare) with maximum gradient strength of 300 mT/m and maximum slew rate of 200 mT/m/ms. The slew rate was de-rated to a maximum of 62.5 mT/m/ms during diffusion encoding to prevent physiological stimulation. A custom-made 64-channel phased array head coil was used for signal reception (Keil et al. 2013).

As a proof of concept, diffusion MRI data with large voxel size (2.4 mm isotropic) and long scan time (108 minutes) for high signal-to-noise ratio (SNR) were acquired in a single healthy subject (Table 1, Protocol #1). Contiguous sagittal images were acquired with the field-of-view (FOV) centered on the midline corpus callosum, including most of the brain parenchyma while excluding the lateral temporal lobes. A two-dimensional (2D) single-refocused diffusion-weighted pulsed gradient spin echo echo planar imaging (DW-PGSE-EPI) sequence was used with the following parameters: echo time/repetition time (TE/TR)=85/3900 ms, 2.4 mm isotropic resolution, three diffusion times Δ=16, 36 and 56 ms, diffusion gradient pulse duration δ=8 ms, eight diffusion encoding gradient strengths evenly spaced between 30–290 mT/m, 64 diffusion encoding gradient directions uniformly distributed on a sphere, one interspersed b=0 image volume for every 16 DW images (DWIs), and parallel imaging using generalized autocalibrating partially parallel acquisitions (GRAPPA) with an acceleration factor of R=2. The maximum b-value at the longest diffusion time was 20,550 s/mm². The total acquisition time was 108 minutes.

Table 1.

Diffusion MRI acquisition parameters. The table lists spatial resolution, diffusion time (Δ), diffusion encoding gradient duration (δ) and gradient strengths, and the number of diffusion encoding gradient directions.

Protocol	Spatial Resolution (mm3)	∆ (ms)	δ (ms)	Gradient Strengths (mT/m)	# of Gradient Directions
#1	2.4×2.4×2.4	16, 36, 56	8	31, 68, 105, 142, 179, 216, 253, 290	64
#2	2×2×2	19	8	31, 68, 105, 142	32
				179, 216, 253, 290	64
		49	8	31, 68, 105	32
				142, 179, 216, 253, 290	64

A shortened protocol (Table 1, Protocol #2) suitable for scanning multiple subjects was used to acquire data in all 20 healthy subjects using the 2D single-refocused DW-PGSE-EPI sequence with the following parameters: TE/TR=77/3800 ms, 66 to 70 contiguous sagittal slices to achieve whole brain coverage, 2 mm isotropic resolution, Δ=19 and 49 ms, δ=8 ms, eight diffusion encoding gradient strengths evenly spaced between 30–290 mT/m, 32 diffusion encoding directions uniformly distributed on a sphere for b<2400 s/mm², 64 diffusion encoding directions for b>=2400 s/mm², one interspersed b=0 image volume for every 16 DWIs, GRAPPA acceleration factor R=2, and simultaneous multislice (SMS) (Setsompop et al. 2012) acceleration factor of 2. The maximum b-value at the longest diffusion time was 17,800 s/mm². The total acquisition time was 55 minutes.

T₁-weighted MRI data were acquired for each subject using a multi-echo magnetization-prepared rapid acquisition gradient echo (ME-MPRAGE) sequence (van der Kouwe et al. 2008), with the following parameters: TE/TR=1.15, 3.03, 4.89, 6.75/2530, inversion time (TI)=1100 ms, flip angle = 7°, 1 mm isotropic resolution, whole brain coverage, and GRAPPA acceleration factor R=2.

Data Preprocessing

All MRI data were corrected for gradient nonlinearity using in-house code (Fan et al. 2016). Diffusion MRI data were also corrected for eddy current induced image distortions using the “eddy” (Andersson and Sotiropoulos 2016; Andersson et al. 2016) functions from the FMRIB Software Library (Jenkinson et al. 2012; Smith et al. 2004) (FSL, https://fsl.fmrib.ox.ac.uk).

Axon Diameter Estimation

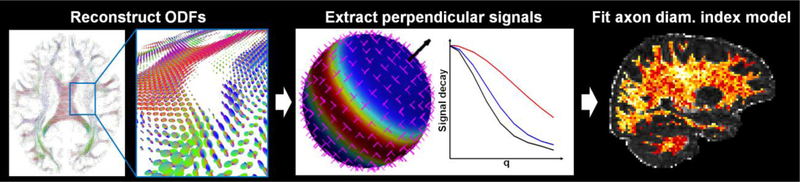
We sought to recover estimates of axon diameter index and restricted volume fraction along the principal fiber orientation from the corrected multi-diffusion time and gradient strength diffusion MRI data by adopting a straightforward analysis method modeled after the AxCaliber approach (Assaf et al. 2008). The data analysis stream is outlined in Figure 1 and described in detail in (Fan et al. 2018). In brief, generalized q-sampling imaging analysis (Yeh et al. 2010) was performed on the q-shell data from the shortest diffusion time (Δ=16 ms for the 2.4 mm isotropic resolution acquisition, Δ=19 ms for the 2 mm isotropic resolution acquisition) in each voxel to identify the principal fiber orientation (i.e., the orientation of the global maximum of the recovered orientation distribution function (ODF)). The mean signal perpendicular to the principal fiber orientation was obtained following the procedure described in (Tuch 2004). Specifically, the signal for each diffusion direction was first resampled to the equator perpendicular to the principal fiber orientation using a Gaussian weighting function dependent on the distance of each diffusion direction from the equator. The resampled signals were then averaged across all directions to obtain the mean perpendicular signal.

Fig. 1.

Flowchart outlining the axon diameter index analysis stream. Using the diffusion-weighted images for the shortest diffusion time, the orientation distribution functions (ODFs) were first reconstructed in each voxel using generalized q-sampling imaging analysis. The principal fiber orientations (black arrow) were calculated for each ODF. The diffusion signals were then resampled to the equator perpendicular to the primary fiber orientation and averaged to obtain the mean signal perpendicular to the principal fiber orientation. A three-compartment model of intra-axonal, extra-axonal, and free water diffusion was fitted to the mean perpendicular signal to obtain estimates of axon diameter and restricted volume fraction

A three-compartment model of intra-axonal, extra-axonal, and free diffusion was fitted to the mean perpendicular signal within the white matter to obtain estimates of axon diameter index, restricted and free diffusion volume fractions, and hindered diffusivity (Huang et al. 2015a). Our approach is similar to the method adopted in AxCaliber (Assaf et al. 2008) but only fits for a single axon diameter index as in ActiveAx (Alexander et al. 2010), as described in our previous work (Fan et al. 2018).

In brief, the signal model for intra-axonal restricted diffusion was obtained from the Gaussian phase distribution approximation (Murday and Cotts 1968) of restricted diffusion in impermeable parallel cylinders of diameter a (van Gelderen et al. 1994; Wang et al. 1995). The extra-axonal hindered diffusion was modeled by the one-dimensional Stejskal-Tanner equation parameterized by the hindered diffusion coefficient D_h (Stejskal and Tanner 1965). Free diffusion in cerebrospinal fluid (CSF) was modeled as isotropic Gaussian diffusion occurring with diffusion coefficient D_csf. The overall signal was taken to be the sum of the intra-axonal, extra-axonal, and CSF compartment signal models weighted by their respective volume fractions: f_r for the intra-axonal compartment, f_csf for the CSF compartment, and f_h = 1 - f_r - f_csf for the extra-axonal compartment. The signal model is detailed in Appendix A, and further discussion regarding the sensitivity of this model to axon diameter at high b-values is detailed in Appendix B.

Markov chain Monte Carlo (MCMC) simulations were performed to obtain samples of the posterior distributions of the model parameters (a, f_r, f_csf, D_h) given the data. Broad uniform priors with the ranges given in parentheses were used for the axon diameter index a (0.1–20 μm), restricted fraction f_r (0–1), and CSF fraction f_csf (0–1). The restricted diffusion coefficient D_r was set to 1.7 μm²/ms, which is comparable to the estimated in vivo axial diffusivity in white matter and in keeping with values used in prior studies (Alexander et al. 2010; Huang et al. 2015a). The diffusion coefficient of CSF (D_csf) was assumed to be that of free water at 37ºC (3 μm²/ms). A Rician noise model was adopted for parameter estimation as in (Alexander 2008; Alexander et al. 2010). The standard deviation of the noise σ = 0.05 was estimated from fitting the noise level in the data and corresponded to an SNR of 20. MCMC samples were saved at intervals of 100 iterations after an initial burn-in period of 20,000 iterations. The total number of MCMC samples calculated for each voxel was 1,800. The mean and standard deviation of the estimates for axon diameter index a, restricted fraction f_r, and CSF fraction f_csf were then calculated for each voxel by taking the mean and standard deviation over the MCMC samples. To demonstrate the robustness of the estimates obtained by the MCMC fitting, the MCMC chains for a and f_r are shown in Figure S1a and S1b. We tested the variability of the estimates by performing a trial of 500 runs, fitting for a and f_r after initializing from an initial value selected from a uniform random distribution of values within the limits specified in the original manuscript (1–20 m for a, 0–1 for f_r). Figure S1a and S1b show the chain convergence for a and f_r, and the distributions of final estimates from 500 trials initialized from a randomly chosen starting point are narrowly peaked about the estimated values after discarding samples from the burn-in period and thinning as described above.

Diffusion Tensor and NODDI Fitting

A diffusion tensor model was fitted to the b=950 s/mm² data using FSL’s “dtifit” function to derive fractional anisotropy (FA) maps. Neurite orientation dispersion and density imaging (NODDI) (Zhang et al. 2012) fitting was also performed to derive maps of orientation dispersion index (ODI) using the NODDI toolbox (https://www.nitrc.org/projects/noddi_toolbox). A subset of the acquired diffusion MRI data (b=950 s/mm² with 32 diffusion encoding directions and b=2,400 s/mm² with 64 diffusion encoding directions) that follows the recommended NODDI protocol were used for NODDI fitting.

Image Co-registration

Cortical surface reconstruction and volumetric segmentation was performed on the T₁-weighted images using FreeSurfer (https://surfer.nmr.mgh.harvard.edu) (Dale et al. 1999). Diffusion images (b=0 image) were co-registered to the T₁-weighted images using the boundary based registration function “bbregister” in FreeSurfer. The derived affine transformation was used to transform the binarized masks of white matter parcellation from FreeSurfer (aparc+aseg.mgz) to diffusion image space.

To quantify axon diameter indices in different tracts, the Johns Hopkins University (JHU) white-matter probabilistic tractography atlas (Mori et al. 2008) was used to create regions of interest (ROIs) in each subject’s native diffusion space. Specifically, the FA map of each subject was first linearly registered to the template FA map in the JHU atlas using NiftyReg’s “reg_aladin” function (https://cmiclab.cs.ucl.ac.uk/mmodat/niftyreg). The linearly transformed FA map was then non-linearly registered to the template FA map using NiftyReg’s “reg_f3d” function. The maps of axon diameter index and restricted volume fraction estimates of each subject were transformed to the JHU template space for group averaging. The transformation was also inverted to transform the probabilistic tractography maps (thresholded at 25%) of selected white matter tracts from atlas space to each subject’s native diffusion space to define the ROIs for specific white matter tracts. The tracts selected for analysis had the highest mean FA values among the 20 white matter tracts in the JHU atlas, including the bilateral corticospinal tracts (CST), cingulum, temporal portions of the superior longitudinal fasciculus (SLF), the forceps major and forceps minor.

Statistical Analysis

The mean axon diameter index and intra-axonal volume fraction averaged along the white matter tracts selected from the analysis described above were compared for each healthy subject using the nonparametric Wilcoxon matched-pairs signed rank test. The statistical analysis was carried out using MATLAB software (MathWorks, Natick, Massachusetts).

Results

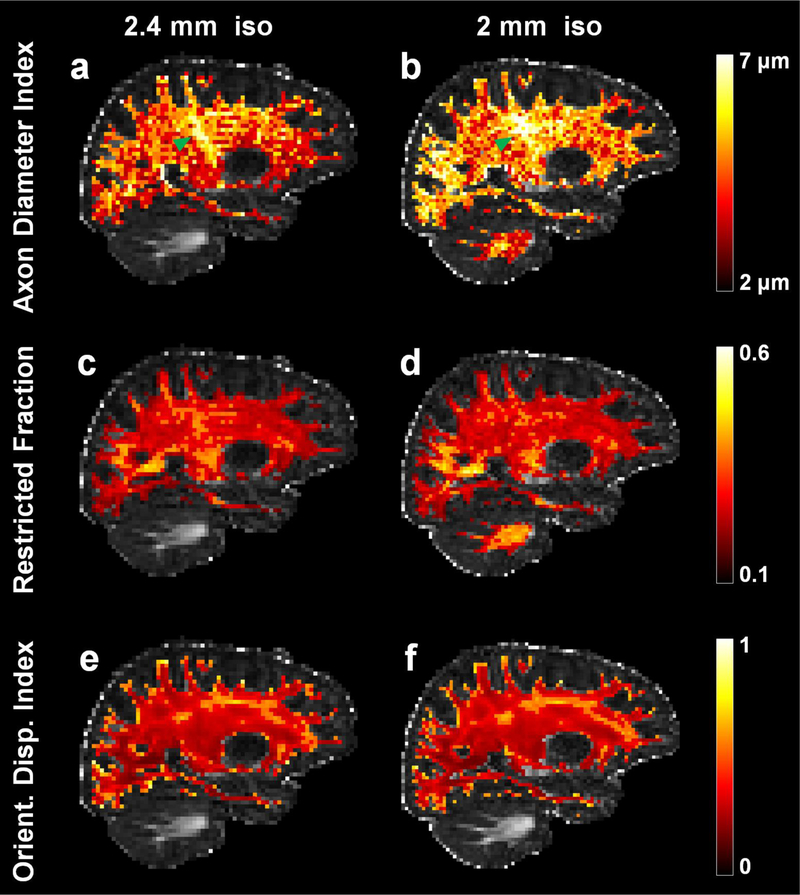
Estimates of mean axon diameter index and restricted volume fraction were consistent across major white matter tracts in the same subject scanned at two different spatial resolutions. Figure 2 shows that axon diameter index and restricted volume fraction estimates in the corticospinal tracts (Fig. 2a, b green arrow heads) were consistently larger (~5–6 μm) compared to the surrounding white matter (~4 μm) at both 2 mm and 2.4 mm isotropic spatial resolution in the same healthy subject, in keeping with histologic trends (Graf von Keyserlingk and Schramm 1984). The orientation of the corticospinal tracts appeared relatively uniform without marked dispersion, as evidenced on the ODI maps (Fig. 2e, f), indicating that the larger axon diameter indices in the corticospinal tracts were not driven by increased orientation dispersion.

Fig. 2.

Representative sagittal slices through the right corticospinal tract (highlighted by green arrowheads) from the maps of axon diameter index (a, b), restricted volume fraction (c, d), and orientation dispersion index (ODI) (e, f) at 2 mm (a, c, e) and 2.4 mm (b, d, f) isotropic resolution in separate scan sessions in the same healthy subject

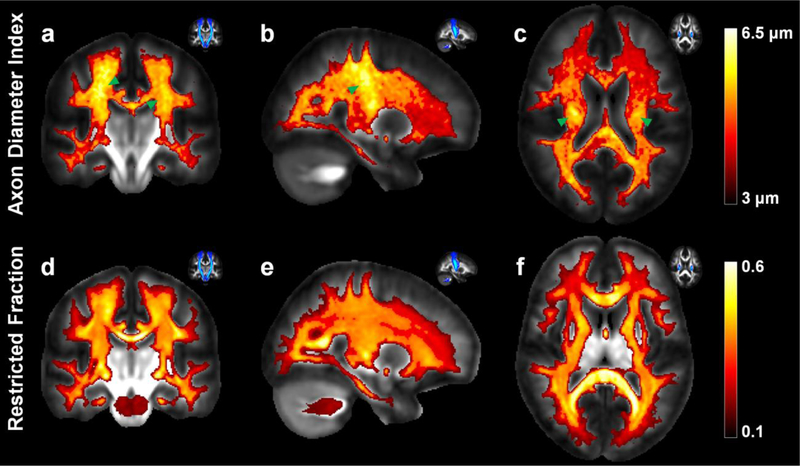
Figure 3 shows the maps of axon diameter index and restricted volume fraction averaged over all 20 healthy subjects in the JHU atlas space. Larger axon diameter indices were consistently observed in the corticospinal tracts compared to surrounding white matter (Fig. 3a–c green arrow heads). An anterior-to-posterior gradient was also observed on the group-averaged axon diameter index map, with smaller diameter indices observed in the frontal lobes and larger diameter indices observed in the parietal and occipital lobes (Fig. 3e, f). In comparison, the restricted volume fraction was relatively uniform throughout these regions (Fig. 3d–f). The trends observed on the group-averaged maps were also seen on the single subject maps, as indicated in Figure 2, but became more evident following group averaging.

Fig. 3.

Group averaged maps of (a–c) axon diameter index estimates and (d–f) restricted volume fraction estimates averaged across 20 healthy subjects, shown in coronal (a, d), sagittal (b, e) and axial views (c, f). The location of the corticospinal tract is highlighted by the green arrowheads and displayed in the probabilistic tractography maps in the top left corner of each sub-figure for reference

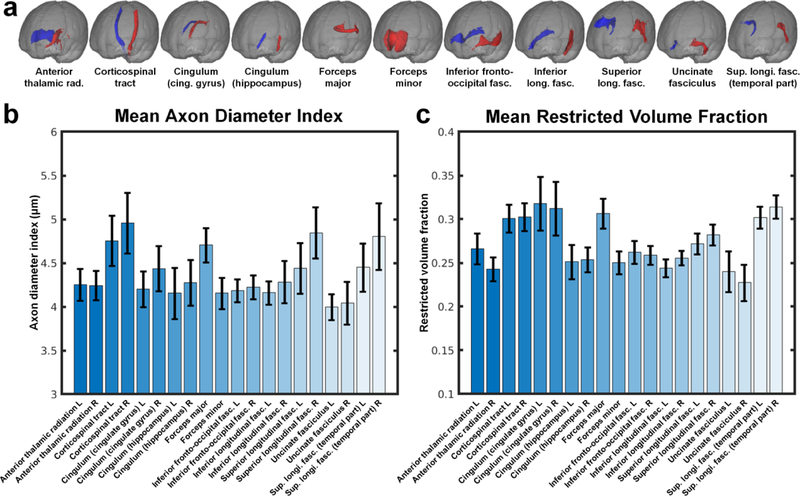
Figure 4 shows the mean and standard deviation of the axon diameter index (Fig. 4a) and restricted volume fraction estimates (Fig. 4b) within selected white matter tracts across all 20 healthy subjects. The mean axon diameter indices within the corticospinal tracts were significantly larger than the mean axon diameter indices within the orthogonally directed cingulum (4.76±0.29 μm vs. 4.20±0.21 μm, p=0.00022 for the left hemisphere, 4.96±0.35 μm vs. 4.44±0.26 μm, p=0.00034 for the right hemisphere). The forceps major also showed significantly larger mean axon diameter index compared to the forceps minor (4.71±0.20 μm vs. 4.16±0.18 μm, p=0.000089). The axon diameter indices within the temporal portion of the superior longitudinal fasciculus were larger than those in the forceps minor (4.45±0.28 μm vs. 4.16±0.18 μm, p=0.00022 for left SLF, 4.81±0.38 μm vs. 4.16±0.18 μm, p=0.000089 for right SLF). The CST, cingulum, and temporal portion of the SLF on the right side all showed larger axon diameter indices compared to the tracts on the left side (4.96±0.35 μm vs. 4.76±0.29 μm, p=0.0028 for the right and left CST; 4.44±0.26 μm vs. 4.20±0.21 μm for the right and left cingulum, p=0.0036; and 4.81±0.38 μm vs. 4.45±0.28 μm for the right and left temporal portions of the SLF, p=0.0045). No significant difference in restricted volume fraction was observed among the selected tracts except for the forceps minor, which showed significantly reduced restricted volume fraction compared to the other tracts.

Fig. 4.

Mean and standard deviation of the (b) mean axon diameter index and (c) mean restricted volume fraction estimates of the 20 major white matter tracts from the JHU white matter atlas (a) averaged across 20 healthy subjects.

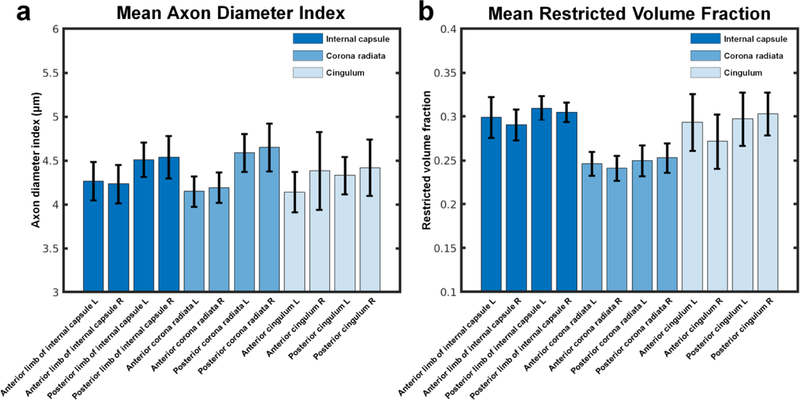
Figure 5 shows the mean and standard deviation of the axon diameter index (Fig. 5a) and restricted volume fraction estimates (Fig. 5b) within the anterior and posterior parts of six selected white matter tracts, including the left and right internal capsule, corona radiata, and cingulum from the JHU white matter atlas averaged across 20 healthy subjects. The mean axon diameter index of the posterior parts of five of the six selected tracts was found to be larger than the mean axon diameter index of the anterior parts (p=0.001, 0.0001, 0.0001, 0.0001, 0.0137, 0.8519 for the left and right internal capsule, corona radiata and cingulum, respectively).

Fig. 5.

Mean and standard deviation of the (a) mean axon diameter index and (b) mean restricted volume fraction estimates of the anterior and posterior parts of six selected major white matter tracts from the JHU white matter atlas averaged across 20 healthy subjects. The six white matter tracts included the left and right internal capsule, left and right corona radiata, and left and right cingulum.

Discussion

In this work, we performed in vivo mapping of axon diameter index and restricted volume fraction throughout the whole brain in 20 healthy subjects using state-of-the-art hardware and imaging protocols. Our results showed clear differences in axon diameter index in the major white matter tracts that are consistent within and between multiple healthy subjects. Our analysis revealed significantly larger axon diameter indices in the corticospinal tracts compared to adjacent white matter tracts such as the cingulum. We also observed an anterior-to-posterior gradient in axon diameter index, with smaller diameter indices observed in the frontal lobes and larger diameter indices in the parieto-occipital white matter.

The trends in axon diameter index estimated from diffusion MRI in this group of healthy subjects are in agreement with neuroanatomical data obtained in non-human primates (Innocenti et al. 2014; Tomasi et al. 2012) and humans (Liewald et al. 2014). We found that axons within the corticospinal tracts were among the largest diameter axons within the human brain, as supported by findings from previous histological studies in humans (Graf von Keyserlingk and Schramm 1984) and non-human primates (Tomasi et al. 2012). The fiber orientations within the corticospinal tracts were fairly homogeneous as indicated by low orientation dispersion, suggesting that the larger diameter indices observed in these tracts were not driven by splaying of the fibers. The observations of smaller diameter indices in the frontal lobes (e.g., forceps minor) and larger diameter indices in the parietal and occipital lobes (e.g., corticospinal tracts and forceps major) are also supported by prior studies in non-human primates demonstrating thinner axons arising from the prefrontal and temporal areas compared to the primary motor, somatosensory, and visual areas (Tomasi et al. 2012).

The larger axon diameter indices observed in the temporal portions of the superior longitudinal fasciculus compared to the forceps minor agree with electron microscopic data in postmortem human brains demonstrating larger average axon diameter in the SLF compared to the transitional zone between the temporal and frontal lobe (Liewald et al. 2014). The same electron microscopy study also demonstrated some evidence for asymmetry between axon diameters between the left and right hemispheres in at least one of the human brains dissected in that study, with larger diameter axons detected in the right SLF compared to the left SLF (Liewald et al. 2014). Studies on the lateralization of axonal diameter are very limited, and definitive validation of axon diameter differences between the right and left corticospinal tracts, for instance, was not found on a review of the literature. However, other literature has suggested that the level of coherence on electroencephalography is generally higher in the right hemisphere compared to the left, which has been used as evidence to support the asymmetry of axon diameter between hemispheres, with the higher level of neural coherence thought to reflect faster axonal conduction and faster conduction associated with thicker axons (Miller 1996). The observed differential in axon diameter index across cerebral hemispheres within this small group of healthy subjects is certainly intriguing but should be interpreted with caution in the absence of definitive validation.

Our work leverages the 300 mT/m gradient strengths available on a scanner constructed for the Human Connectome Project and applies cutting-edge techniques for accelerating slice and in-plane image acquisition to sample a wide range of gradient strengths and diffusion strengths at 2 mm isotropic spatial resolution throughout the whole brain. We adopted a simple yet robust analysis method to estimate axon diameter index and restricted volume fraction in white matter tracts of arbitrary orientation by resampling the signal perpendicular to the primary fiber orientation, similar to the established AxCaliber technique (Assaf et al. 2008). Given the ample diffusion data available for fitting, we chose to apply an analysis that would minimize the number of estimated parameters but still reflect the underlying microstructure captured in the diffusion signal decays. The diffusion signal decays calculated from the average perpendicular signal had relatively high signal-to-noise ratio, which made model-fitting fairly straightforward and robust. This approach has been previously shown to recover known compartment sizes and volume fractions using data generated from random-walk diffusion simulations and experimentally validated in a biomimetic brain phantom with textile axons of a known manufactured diameter (Fan et al. 2018).

Limitations

While the maps of axon diameter index obtained using the current acquisition and analysis method are consistent with trends from histology, the range of values reported here (~2–6 m) are known to overestimate the majority of axon diameters in the human brain by nearly an order of magnitude. This is a well-known problem with existing approaches to axon diameter estimation using diffusion MRI and drives at a number of limitations related to diffusion modeling and acquisition. The use of a single axon diameter to summarize the average compartment size biases the estimation to larger diameter axons, which contain more water and have a greater contribution to the overall diffusion signal decay compared to the highly restricted water within small diameter axons (Alexander et al. 2010). Furthermore, although the use of higher maximum gradient strengths has been shown to decrease estimates of axon diameter in vivo (Huang et al. 2015a) and improve the contrast and stability of these estimates (Dyrby et al. 2013), axons smaller than ~3 m remain below the diffusion resolution limit at 300 mT/m (Nilsson and Alexander 2012; Nilsson et al. 2017). Finally, the time-dependence of water diffusion in the extra-axonal space was not accounted for and could conceivably bias the estimates of axon diameter to larger values (Burcaw et al. 2015; De Santis et al. 2016; Fieremans et al. 2016; Novikov et al. 2014).

The sensitivity to small diameter axons could be improved in a number of ways. Even higher gradient strengths and slew rates beyond the Connectome scanner capabilities (i.e. >300 mT/m and >200 mT/m/s) as well as shorter diffusion times would be needed to probe restricted diffusion within smaller compartments. Taking the diffusion time Δ in the pulsed gradient spin echo diffusion experiment to be roughly on the order of a²/2D_r (Callaghan 1991), the mean diffusion displacements for the range of diffusion times used in our experiments (16–56 ms) would be expected to be 7–14 μm, assuming an intra-axonal diffusivity of 1.7 μm²/ms. The application of oscillating gradients could help to achieve shorter diffusion times and probe smaller length scales (Does et al. 2003; Gore et al. 2010; Xu et al. 2014). Sensitivity to the smallest axons could also be gained by optimizing the diffusion-encoding gradient waveform rather than using the standard pulsed gradient spin echo experiment, particularly at lower gradient strengths (Drobnjak et al. 2010; Siow et al. 2012). In addition to factoring in the time-dependence of extra-axonal diffusion, a “stick” or sub-micron compartment could be incorporated into the model to account for highly restricted water within small axons that is essentially unattenuated and below the experimental sensitivity of diffusion MRI (Alexander et al. 2010; Benjamini et al. 2016).

We sought to provide a straightforward approach to estimating axon diameter index and volume fraction in white matter tracts of arbitrary orientation while minimizing the number of fitted parameters. A key limitation of our approach is that it assumes a single fiber in each voxel and only considers the signal perpendicular to the principal fiber orientation. Thus, the current approach does not account for crossing fibers. However, we have performed detailed simulations and experimental validation of diameter indices using this single fiber model in a well-characterized biomimetic phantom composed of parallel and crossing fibers of known diameter (Fan et al. 2018). Our results show that restricted volume fraction estimates are more severely affected than axon diameter index in the presence of crossing fibers using the single fiber model. Nevertheless, recognizing the potential limitations of the single fiber model, we performed ROI analysis on well-defined, largely unidirectional white matter tracts with high fractional anisotropy. Using the mean perpendicular signal for an assumed single fiber population resulted in higher signal-to-noise ratio in the diffusion signal decay curves and reliable parameter estimation. In the end, we were able to recover consistent estimates of axon diameter index and volume fraction in the major white matter bundles analyzed here across multiple healthy subjects.

Future iterations of this work will focus on fitting a generalized model that accounts for fiber orientation, compartment size, and restricted volume fraction for multiple fiber populations in each voxel. Similar approaches have been suggested by others, including the combined hindered and restricted model of water diffusion (CHARMED) (Assaf and Basser 2005), AxCaliber 3D (Barazany et al. 2011), and ActiveAx (Alexander et al. 2010). While fitting for multiple fiber populations would account for crossing fibers, the greater number of estimated parameters would make the fitting non-trivial, and techniques such as convex optimization could be used to linearize the fitting problem and accelerate the calculation (Daducci et al. 2015a), rather than using the precise but computationally expensive nonlinear fitting procedure that we have adopted here. The application of automated fiber quantification tools (Yeatman et al. 2018) to multifiber axon diameter estimation would enable the assessment of axon diameter variability within and along tracts with greater accuracy and specificity compared to our current approach of averaging single fiber axon diameter estimates within regions-of-interest defined by an atlas.

In this work, we use a simple geometric model to infer basic metrics of compartment size and packing density for white matter fibers of arbitrary orientation within a complex tissue microenvironment. Although our model resulted in larger estimates than expected from histology, the contrast for axon diameter index in the major white matter tracts, e.g., corpus callosum and corticospinal tract, largely matched the expected trends from histology. Rather than serving as fully quantitative measures of axon diameter and density, our results may be considered as axon diameter- and volume fraction-weighted images that may capture broad trends in axonal size and packing density. We acknowledge that while our model of axon diameter explains the data and is consistent with prior literature, providing fairly robust fitting and replicable results across subjects that seems to be modulated by the microstructure, the precise ways in which the microstructure influences the diffusion MRI signal and the exact microstructural origins of the contrast we are observing merit more in-depth analysis and further investigation, which we anticipate will be facilitated by the availability of high gradient strengths for in vivo human imaging.

Another limitation of this work was the lack of estimation of the intra-axonal diffusion coefficient within and across subjects. In the fitting approach used here, we fixed the intra-axonal diffusivity to 1.7 μm²/ms, in line with estimates from prior studies (Alexander et al. 2010), to avoid the indeterminacy of the model solutions (Jelescu et al. 2016; Novikov et al. 2018) and reduce the number of fitted parameters, which would otherwise add complexity to the model. The intra-axonal diffusion coefficient may vary across the brain, as suggested by findings from diffusion-weighted MR spectroscopy (Ellegood et al. 2011), where the mean diffusivity of N-acetylaspartate, a metabolite primarily localized within neurons and axons, was found to vary by up to 20–30% between different white matter tracts. It is difficult to infer the actual impact of the spatial variation in intra-axonal diffusivity on the resulting whole-brain estimates of axon diameter index and restricted volume fraction without fitting explicitly for this parameter. We attempted to determine the degree of variation in intra-axonal parallel diffusivity and its impact on the obtained solutions of the equation across the whole brain by fitting explicitly for the intra-axonal parallel diffusivity in a representative subject, allowing D_r and D_h to vary independently in the range of 0 to 3 μm²/ms, within the constraint that D_r > D_h. We then compared the parameter maps to those obtained with a fixed intra-axonal diffusivity of 1.7 μm²/ms. We found that the intra-axonal diffusivity in white matter varied between 1.0 and 2.4 μm²/ms, in line with findings from other groups (Dhital et al. 2019; Veraart et al. 2019), with the majority of voxels falling between 1.7 and 1.9 μm²/ms. Moreover, the estimates of axon diameter index, restricted volume fraction, and hindered diffusivity across the brain were very similar to the results obtained with a fixed intra-axonal diffusivity of 1.7 μm²/ms, leading us to conclude that the spatial variation of intra-axonal diffusivity across the brain did not significantly affect the fitted parameters in our approach.

Applications

Our approach provides some measure of axon diameter index throughout the whole brain, which can vary considerably between different cortical regions, and shows the potential for distinguishing between fiber systems based on the underlying microstructure. Knowledge of the axon diameter index and density along specific tracts could be used to inform models of structural connectivity and clarify ambiguities occurring at fiber crossings and other complex fiber configurations, as suggested by other groups (Daducci et al. 2015b; Zhang et al. 2011). The local microstructure information can also be integrated into the tract reconstruction by assuming that the axon diameter along a tract should be coherent, as demonstrated in a recently proposed method known as AxTract (Girard et al. 2017). The AxTract method used local axon diameter estimates obtained from an efficient convex optimization approach to refine the tractography by choosing the fiber propagation direction that would minimize the change in axon diameter index (Girard et al. 2017). AxTract does not depend on the specific white matter model implemented, but rather utilizes the differences in axon diameter between fiber bundles to refine fiber tracking. In contrast, our current approach does not incorporate tractography into the estimation of axon diameter but rather provides maps of axon diameter index and volume fraction throughout the whole brain, agnostic to the underlying fiber bundles. The two approaches are complementary, and incorporating information about fiber propagation angle and fiber bundle coherence to constrain our estimates of axon diameter index would be a fruitful avenue for future investigation.

By assessing the relative size and packing density of axons in the human brain in vivo, high-gradient diffusion MRI serves as a noninvasive tool for probing the underlying neurophysiology as well as alterations that occur in learning and aging. The relationship between axon diameter index and conduction velocity suggests that axon diameter mapping methods could be used to infer the speed at which information is processed in the brain (Horowitz et al. 2015) and provide a window into the microstructural alterations that occur in neuroplasticity (Tavor et al. 2013). Conventional neuroanatomical methods applied in postmortem human studies have shown increasing axon diameter with age (Aboitiz et al. 1996), and changes in axon diameter may also correlate with the stages of development (Bjornholm et al. 2017).

Previous studies have indicated that certain populations of axons may be more vulnerable to injury in a variety of neurodegenerative disorders. Small diameter axons appear to be selectively damaged in multiple sclerosis (DeLuca et al. 2004; Lovas et al. 2000), whereas large diameter axons are more severely affected in amyotrophic lateral sclerosis (Cluskey and Ramsden 2001; Tandan and Bradley 1985). Whole-brain axon diameter mapping could also be invaluable in the study of psychiatric disorders, which are hypothesized to result from abnormal signaling. Several studies have focused on abnormalities in axonal projections between association areas, particularly in the prefrontal and temporal regions, and their involvement in a number of neuropsychiatric disorders, including autism (Kumar et al. 2010; Noriuchi et al. 2010) and schizophrenia (Innocenti et al. 2003; Uhlhaas and Singer 2011) and Alzheimer disease (Di Paola et al. 2010). With the known link between axon diameter and conduction velocity, maps of axon diameter index could be used for correlation studies with brain function using fMRI and serve as a potential biomarker for the involvement of specific white matter tracts in these neuropsychiatric conditions, among others.

Conclusion

In this study, we provide an approach to estimating indices of axon diameter and volume fraction across fiber bundles of arbitrary orientation in the in vivo human brain using gradient strengths up to 300 mT/m. Our model provides estimates of axon diameter index across the main fiber pathways in the brain that are replicable across subjects and consistent with the experimental data. The agreement between our findings and histological observations is encouraging and suggests that our measurements are modulated by the underlying tissue microstructure. While the precise origin of such modulation requires further elucidation, our current results provide plausible relative estimates of axon diameter index across white matter tracts and offer a framework and benchmark dataset for further investigation of the relationship between the diffusion MRI signal and the complex tissue microstructure in the human brain, facilitated by the availability of high gradient strengths for in vivo human imaging.

Appendix A

The overall signal model is taken to be the sum of the intra-axonal, extra-axonal, and CSF compartment signal models weighted by their respective volume fractions: f_r for the intra-axonal compartment, f_csf for the CSF compartment, and f_h = 1 - f_r - f_csf for the extra-axonal compartment:

$$S=f_r{S}_r+f_h{S}_h+f_{csf}{S}_{csf}$$ (A1)

The signal model for intra-axonal restricted diffusion is obtained from the Gaussian phase distribution approximation (Murday and Cotts 1968) of restricted diffusion in impermeable parallel cylinders of diameter a (van Gelderen et al. 1994; Wang et al. 1995), which accounts for diffusion during the gradient pulse when the pulse duration is on the order of the diffusion time Δ:

$$S_r=S_0\text{exp}\left\{-2{\gamma }^2{G}^2{\sum }_{m=1}^{\infty }\frac{\left[2D_r{\alpha }_m^2\delta -2+2e^{-D_r{\alpha }_m^2\delta }+2e^{-D_r{\alpha }_m^2\mathrm{\Delta }}-e^{-D_r{\alpha }_m^2(\mathrm{\Delta }-\delta )}-e^{-D_r{\alpha }_m^2(\mathrm{\Delta }+\delta )}\right]}{D_r^2{\alpha }_m^6\left[{\left(a/2\right)}^2{\alpha }_m^2-1\right]}\right\}$$ (A2)

where S₀ is the signal obtained at b=0 without diffusion weighting, γ is the gyromagnetic ratio, G is the gradient strength of the diffusion-encoding gradients, D_r is the diffusion coefficient of water in the restricted compartment, and m are the roots of the equation

$${J^{\prime }}_{\hspace{0.17em}1}\left({\alpha }_m\hspace{0.17em}*\hspace{0.17em}a/2\right)=0$$ (A3)

where ${J^{\prime }}_1$ is the derivative of the Bessel function of the first kind, order one. The summation in Equation 1 was taken up to m=10, with the contribution of terms m>10 considered negligible. Instead of imposing a gamma distribution of axon diameters (Assaf et al. 2008), we only fitted for a single axon diameter as in (Alexander et al. 2010).

The extra-axonal hindered diffusion is modeled by the one-dimensional Stejskal-Tanner equation parameterized by the hindered diffusion coefficient D_h (Stejskal and Tanner 1965):

$$S_h=S_0\text{exp}[-{\left(\gamma G\delta \right)}^2\left(\mathrm{\Delta }-\delta /3\right)D_h].$$ (A4)

Free diffusion in cerebrospinal fluid (CSF) is modeled as isotropic Gaussian diffusion occurring with diffusion coefficient D_csf (Barazany et al. 2009):

$$S_{csf}=S_0\text{exp}[-{\left(\gamma G\delta \right)}^2\left(\mathrm{\Delta }-\delta /3\right)D_{csf}].$$ (A5)

Appendix B

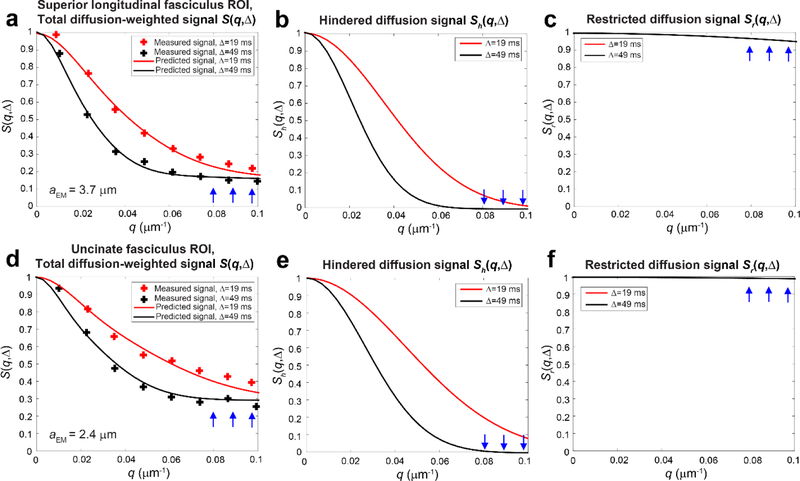
To support the sensitivity of our measurements to intra-axonal water diffusion using strong diffusion weighting, we performed the following analysis in two white matter ROIs with different effective axon diameters. We take advantage of the fact that at high b-values, the dominant contribution to the diffusion MRI signal is from the intra-axonal compartment. Here, we plotted the measured average signal perpendicular to the principal fiber orientation for ROIs with distinct axon diameter estimates selected from the superior longitudinal fasciculus (SLF) and uncinate fasciculus in a single representative subject from our cohort. We corroborated the sensitivity of our measurements to intra-axonal water diffusion using diameter distributions obtained from electron microscopy. Toward this end, we digitized the diameter distributions of axons in the SLF and uncinate fasciculus presented in Liewald et al. (Liewald et al. 2014). To account for tissue shrinkage following fixation, dehydration and embedding, we multiplied the diameter distributions by a factor of 1.5, as suggested by prior histological (Aboitiz et al. 1992) and MRI studies (Alexander et al. 2010; Veraart et al. 2019). To approximate the effective axonal radius that MRI is sensitive to on the voxel level, we calculated the volume-corrected effective axonal radius, which is dominated by the largest axons within the voxel (Burcaw et al. 2015):

$$r_{eff}=\sqrt[4]{\frac{r^6}{r^2}}$$

We plugged the effective axonal radius estimated from the EM data into the signal model. Figures B.1c and B.1f show the predicted signal decays for restricted diffusion within axons of estimated effective diameter derived from EM in the SLF (a_EM=3.7 m) and uncinate fasciculus (a_EM=2.4 m), which show greater signal decay for the larger diameter axons in the SLF compared to the uncinate fasciculus. The signal decay in the restricted compartment is also reflected at high q-values in the predicted total diffusion-weighted signal (Figs. B.1a and B.1d), which is the sum of the restricted signal predicted from EM (Figs. B.1c and B.1f) and the estimated hindered diffusion signal obtained from fitting the hindered signal model to the experimental data (Figs. B.1b and B.1e). The predicted total diffusion-weighted signal is plotted alongside the measured diffusion MRI signal in regions of interest sampled in the SLF and uncinate fasciculus in a representative subject. Figure B.1a and B.1d show reasonable agreement between the measured and predicted overall diffusion MRI signal S(q, ) for both the SLF and uncinate fasciculus ROIs using the effective axonal diameter derived from the EM data, suggesting that our measurements may be sensitive to intra-axonal water diffusion, returning effective axonal radius estimates that are in the ballpark of those expected from electron microscopy.

Figure B1.

Simulated and experimental diffusion signal decays plotted for (a–c) a region-of-interest (ROI) in the superior longitudinal fasciculus (volume-weighted effective axon diameter of 3.7 m calculated from histograms derived from electron micrographs in Liewald et al. (Liewald et al. 2014)and restricted volume fraction of 0.21 calculated from fitting Equation A1 to the experimental data) compared to (d–f) an ROI in the uncinate fasciculus (volume-weighted effective axon diameter of 2.4 m calculated from histograms derived from electron micrographs in Liewald et al. and restricted volume fraction of 0.30 calculated from fitting Equation A1 to the experimental data). In (a) and (d), the predicted total diffusion-weighted signal S(q, ) is a weighted sum of the signal due to (b, e) hindered and (c, f) restricted water. The restricted diffusion signal is calculated from the effective axon diameter derived from electron microscopy. At high q-values, the contribution to the tail of S(q, ) is dominated by restricted diffusion presumed to arise from the intra-axonal space.