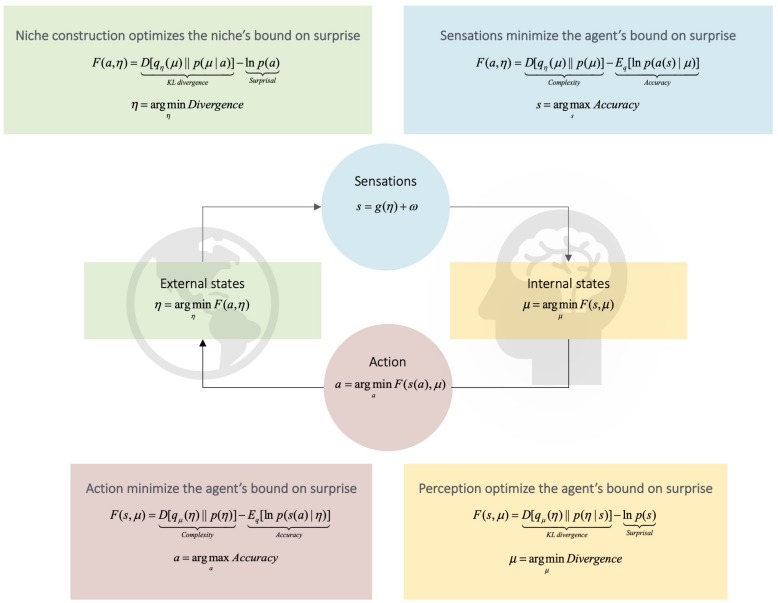
FIGURE 1.

Active inference. This Figure schematizes active inference. It depicts the coupling of an agent’s internal states (the dynamics of which entail predictions or beliefs about the niche, μ) to its external states (the dynamics of the agent’s niche, η). Middle Panel: The influence of the niche on the agent is given by the dynamics of the agent’s sensations, s. Reciprocally, the influence of the agent upon its niche is given by the agent’s action, a, upon the niche. This means that the niche is not directly observable from the perspective of an agent’s internal states; and the agent’s internal states are not directly observable from the perspective of the niche. From an agent’s perspective, the niche is thus described as a set of hidden variables. Hidden variables must be inferred (i.e., predicted) from sensory observations. Thus, to minimize the probability of sampling surprising sensory states, the task for the agent is to attune the dynamics of internal states to those of the niche; or attune the dynamics of the niche to those of internal states. Attunement renders the agent an approximate (predictive) model of the hidden causes of its sensations. We can quantify the degree of attunement between organism and niche with a quantity called variational free energy (Bruineberg et al., 2018a; Constant et al., 2018). Free energy F bounds (i.e., is greater or equal to) the surprisal –lnp(s) associated with a sensation (Friston, 2010). Importantly, free energy is a function of two quantities to which the organism has access, namely, its sensations and predictions (for discussion, see Bruineberg et al., 2018a). Lower Panel: The bottom right details how perception optimizes free energy by implicitly minimizing a Kullback–Leibler (KL) divergence term D. The KL divergence tracks the statistical similarity of two distributions (Cover and Thomas, 1991); e.g., the similarity of prior beliefs about the state of the niche with posterior beliefs (Friston, 2012). Because the KL divergence provides an upper bound on surprisal, minimizing it renders the agent a model of the niche and thus implicitly bounds the surprise of sensory states. Upper Panel: These expressions define the relationship of the niche to the agent. Note the kind of ‘mirror image’ relationship between the equations in the (upper panel) with the equations in the lower. This relationship is a consequence of the mathematics of free energy minimization (see Bruineberg et al., 2018b; Constant et al., 2018). It means that the niche ‘sees’ and ‘learns’ about the agent (i.e., via the agent’s action) in the same way an agent sees and learns about their niche (i.e., via the niche’s ‘action’). This insight is extended in Figure 2. Adapted with permission from Veissière et al. (forthcoming).