Chaos in a nonautonomous eco-epidemiological model with delay

Highlights

• •We propose and analyse a delayed nonautonomous predator-prey model with disease in prey.
• •Derived the sufficient conditions for global asymptotic stability of the positive periodic solutions.
• •Autonomous system develops only limit cycle oscillations through a Hopf-bifurcation for increasing the values of delay.
• •Corresponding nonautonomous system shows chaotic dynamics for increasing the delay parameter.
• •We draw Poincare map and maximum Lyapunov exponent to identify the chaotic behaviour of the system.

Abstract

In this paper, we propose and analyze a nonautonomous predator-prey model with disease in prey, and a discrete time delay for the incubation period in disease transmission. Employing the theory of differential inequalities, we find sufficient conditions for the permanence of the system. Further, we use Lyapunov’s functional method to obtain sufficient conditions for global asymptotic stability of the system. We observe that the permanence of the system is unaffected due to presence of incubation delay. However, incubation delay affects the global stability of the positive periodic solution of the system. To reinforce the analytical results and to get more insight into the system’s behavior, we perform some numerical simulations of the autonomous and nonautonomous systems with and without time delay. We observe that for the gradual increase in the magnitude of incubation delay, the autonomous system develops limit cycle oscillation through a Hopf-bifurcation while the corresponding nonautonomous system shows chaotic dynamics through quasi-periodic oscillations. We apply basic tools of non-linear dynamics such as Poincaré section and maximum Lyapunov exponent to confirm the chaotic behavior of the system.

1. Introduction

The use of mathematical models for analyzing and understanding the spread and control of the infectious diseases has become an extremely important tool. Theoretical biologists, physicists and mathematicians extensively studied the dynamics of ecological models and provided important insights about complex biological processes [1], [2], [3], [4]. In ecology, the predator-prey interactions have a long history and understanding the dynamics of such systems is the most interesting research topic among the scientists across the world. The study of eco-epidemiological systems is the investigation of ecological systems in the presence of epidemiological factors. In this regard, Anderson and May [5] were the first who paved the way of merging ecological and epidemiological systems. The term ’eco-epidemiology’ was coined for such systems by Chattopadhyay and Arino [6]. Afterwards, the study of eco-epidemiological models and their biological significances have gained much attention among the researchers [7], [8], [9], [10], [11], [12], [13], [14], [15]. In nature, species do not survive alone, they compete with the other species in the environment for space, food and predation. Understanding the effect of parasites on biodiversity and ecosystem dynamics is an important issue in conservation biology. The dynamics of host population can be regulated by disease, and also depend on the other members of the host’s community, such as predators. Moreover, the shape and the community structure of an ecosystem can be dramatically changed by the predatory activities. The invasion of parasites into the host population may be prevented by predators. Due to these facts, the research on eco-epidemiological systems has become more important issue among the scientists worldwide. It plays crucial role in determining the persistence-extinction threshold of populations in the systems of two or more interacting species subjected to parasitism [16], [17], [18].

In the eco-epidemiological systems, the nonautonomous phenomenon frequently happens due to seasonal variations in biological parameters such as growth rate and disease transmission rate which in turn makes the populations to behave periodically [19], [20], [21], [22]. The contact rate of pathogen changes seasonally with peaks in spring and autumn. This seasonal behavior is due to the moderate temperature in spring and autumn, which is favorable for pathogen survival. A nonautonomous predator-prey system is studied by Samanta [21], considering a disease in prey transmitted through direct contact only. He has also considered gestation delay in the modeling process and investigated its effect on the permanence and global stability of the system. He performed mathematical analysis and showed that the time delay has no impact on the permanence of the system, but it affects the global stability. In the present study, we have investigated a similar nonautonomous eco-epidemiological system with incubation delay with an aim to explore rich dynamics.

It is well understood that many of the processes, both natural and man-made, in biology and medicine involved time delays. Time delay occurs often in almost every biological situation. Therefore, investigation of any ecological/epidemiological system without time delay is not realistic [23], [24], [25], [26], [27], [28], [29], [30], [31]. Detailed topics on the use of time delays in real models can be found in the classical books [32], [33], [34]. A plethora of research is available in the literature on the behavior of dynamical systems with retarded systems, such as periodic oscillation, persistence, bifurcation and chaos [35], [36], [37], [38]. In eco-epidemiological systems, time delay involves in the primary infection [39], immune response [40], [41], etc. Passing of infection from one infected individual to another susceptible individual is not an instantaneous process but conceals some time-lags, known as delay due to incubation. The time elapsed between exposure of a susceptible individual to a pathogenic organism, and the individual becomes infectious is called incubation period. The period of incubation depends on the type of diseases, e.g., in case of chickenpox, it is 14–16 days. Several authors have considered incubation delay in the modeling process [42], [43], [44].

Previous studies on ecological/eco-epidemiological modeling mainly concerned about the stability and persistence of the system [45] but in recent years, scientists are interested to investigate more dynamical features such as bifurcations and chaos [2], [46], [47]. The occurrence of chaos in ecological systems made it a subject of paramount interest among the theoretical ecologists [2], [3], [4], [48]. Hastings and Powell [2] first observed chaos in a three-species food chain model, and concluded that chaos is a common phenomenon in nature. Later on, many studies have been conducted with an aim to explore chaotic dynamics in continuous three-species food chain models [19], [49], [50] and/or to control chaos in such systems [51], [52], [53], [54], [55]. Due to rich dynamics, the occurrence of chaos in an ecological system is of considerable interest. It is well documented that many biological and/or environmental processes, such as Allee effect [56], omnivory [50], latency in biological processes [47], [57], large turn over of resource [58], coupling of incommensurate oscillations [59], seasonal forcing [19], [20], noise [60], [61], etc., may produce chaotic dynamics in simple predator-prey systems; out of which the presence of time delay and seasonal forcing can be observed in many biological processes. Recently, Khajanchi et al. [62] showed that the incorporation of realistic time delays in cancer models exhibits deterministic chaos, and significantly increase the dynamical complexity of the tumor-immune competitive system. In eco-epidemiology, presence of delay and seasonal forcing is very common. For example, marine viruses constitute a major ecological and evolutionary driving force in the marine ecosystems [63]. Several studies have demonstrated that natural virus populations can consist of different viruses infective to many algal groups, such as coccolithophorids [64], picoflagellates [65], and dinoflagellates [66], etc. There might be some time delay due to virus reproduction inside infected cells [67]. Moreover, the rate parameters of phytoplankton-zooplankton interactions are time varying and follow positive periodic function with period of one year [22]. Therefore, such complex biological processes can be modelled by system of delayed nonautonomous differential equations.

Here, our aim is to study the impact of incubation delay in a nonautonomous predator-prey system with disease in prey population only. We compare the dynamical behaviors of the nonautonomous systems with and without time delay with the corresponding autonomous systems by using numerical simulations. Rest of the paper is organized as follows: in the next section, biological assumptions and model formulations are given. In Section 3, the existence and uniqueness of the solutions are discussed; also the sufficient conditions for permanence of the system are derived. Conditions for the global stability of the positive periodic solutions are derived in Section 4. In Section 5, numerical simulations are carried out. Finally, the paper ends with a conclusion.

2. The nonautonomous model

Here, we propose a nonautonomous eco-epidemiological model by considering susceptible prey, infected prey and predator populations as state variables. In the region under consideration, let x ₁(t), x ₂(t) and x ₃(t) be the densities of susceptible prey, infected prey and predator population, respectively at time t > 0. Only susceptible prey is assumed to be capable of reproducing following logistic growth, and their mortality rate is of density dependent. We consider that the disease is transmitted from infected individuals to susceptible individuals through contacts. The force of infection is assumed to follow the mass action law i.e., β(t)x ₁(t)x ₂(t). The disease is considered to spread among the prey population only. We also consider that the disease is not genetically inherited. The infected prey neither recovers nor becomes immune. For example, cassava (the natural host) and N. benthamiana, infected with a DNA begomovirus, East African cassava mosaic virus (EACMCV-[CM]), failed to recover [68]. Even human population cannot recover from some communicable diseases, such as HIV/AIDS and Ebola haemorrhagic fever. The hunting rates of predator on the susceptible and infected prey are assumed to be different [69]. Let a ₁(t) and a ₂(t) be rate functions at which the predator hunt the susceptible and infected prey, respectively. The conversion efficiency of the predator population for susceptible and infected prey be c ₁(t) and c ₂(t), respectively. Based on the above ecological assumptions, we have the following nonautonomous eco-epidemiological model,

$$\begin{array}{ccc}\hfill \frac{\text{d}{x}_1\left(t\right)}{\text{d}t}& =& x_1\left(t\right)[r\left(t\right)-k\left(t\right)(x_1\left(t\right)+x_2\left(t\right))-a_1\left(t\right)x_3\left(t\right)-\beta \left(t\right)x_2\left(t\right)],\hfill \\ \hfill \frac{\text{d}{x}_2\left(t\right)}{\text{d}t}& =& x_2\left(t\right)[\beta \left(t\right)x_1\left(t\right)-a_2\left(t\right)x_3\left(t\right)-e\left(t\right)],\hfill \\ \hfill \frac{\text{d}{x}_3\left(t\right)}{\text{d}t}& =& x_3\left(t\right)[-d\left(t\right)-b\left(t\right)x_3\left(t\right)+c_1\left(t\right)x_1\left(t\right)+c_2\left(t\right)x_2\left(t\right)].\hfill \end{array}$$ (2.1)

Here, we assume that the rate parameters are positive, continuous and bounded, and have positive lower bounds. We assume that the rate parameters vary depending on the light intensity, temperature and rainfall. It is to be noted that the maximum temperature is observed in summer, the highest daily average light intensity is observed in winter and the maximum rainfall is observed in monsoon [70]. For simplicity, we neglect this phase shift and simply incorporate the effect of seasonal changes by considering the periodic rate parameters with a period of one year. The biological meanings of parameters involved in the system (2.1) are given in Table 1 .

Table 1.

Biological meanings of parameters in the system (2.1).

Parameters	Descriptions
r(t)	Intrinsic growth rate of susceptible prey
e(t)	Death rate of infected prey
d(t)	Death rate of the predator population
k(t)	Crowding effect on the prey population
b(t)	Crowding effect on the predator population
β(t)	Disease transmission rate
a1(t)	Consumption rate of susceptible prey by predator
a2(t)	Consumption rate of infected prey by predator
c1(t)	Predator’s conversion efficiency from susceptible prey to predator biomass
c2(t)	Conversion efficiency from infected prey to predator biomass

In system (2.1), it is assumed that the disease transmission is instantaneous, i.e., if a susceptible individual comes into contact with an infected individual, the susceptible one becomes infected. However, in reality, this process doesn’t occur instantaneously. After getting infected, the infected individuals take some time to become infectious until the infected agents grow sufficiently inside the body. Therefore, there is a time lag between the process of contact and becoming infectious, known as incubation delay. The incubation period varies depending on the infectious disease. For example, the incubation period of chickenpox is $14-16$ days, $2.8-3.7$ days for human coronavirus, $3.6-4.4$ days for severe acute respiratory syndrome coronavirus, $1.3-1.5$ days for influenza A, $0.5-0.6$ days for influenza B, $11.8-13.3$ days for measles, etc., [71]. To incorporate the incubation delay, we modify system (2.1) as,

$$\begin{array}{ccc}\hfill \frac{\text{d}{x}_1\left(t\right)}{\text{d}t}& =& r\left(t\right)x_1\left(t\right)-k\left(t\right)x_1\left(t\right)(x_1\left(t\right)+x_2\left(t\right))-a_1\left(t\right)x_1\left(t\right)x_3\left(t\right)-\beta \left(t\right)x_1\left(t\right)x_2\left(t\right),\hfill \\ \hfill \frac{\text{d}{x}_2\left(t\right)}{\text{d}t}& =& \beta \left(t\right)x_1(t-\tau )x_2(t-\tau )-a_2\left(t\right)x_2\left(t\right)x_3\left(t\right)-e\left(t\right)x_2\left(t\right),\hfill \\ \hfill \frac{\text{d}{x}_3\left(t\right)}{\text{d}t}& =& -d\left(t\right)x_3\left(t\right)-b\left(t\right)x_3^2\left(t\right)+c_1\left(t\right)x_1\left(t\right)x_3\left(t\right)+c_2\left(t\right)x_2\left(t\right)x_3\left(t\right).\hfill \end{array}$$ (2.2)

Here, the incubation period $\tau \in {\mathbb{R}}_{+}$ is the time during which the infectious agent develops in the host, and only after that time the infected prey becomes itself infectious. Therefore, the number of actively infected prey at time t is arising from the contacts of actual population of susceptible and infected prey at time $(t-\tau ),$ where τ is the discrete time delay. Let C denote the Banach space of continuous functions $\psi :[-\tau ,0]\to {\mathbb{R}}^3$ with norm

$$\parallel \psi \parallel =\underset{-\tau \le \theta \le 0}{\sup }\left\{\right|{\psi }_1\left(\theta \right)|,|{\psi }_2\left(\theta \right)|,|{\psi }_3\left(\theta \right)\left|\right\},$$ (2.3)

where $\psi =({\psi }_1,{\psi }_2,{\psi }_3)$. Initial conditions of system (2.2) are given as

$$x_1\left(\theta \right)={\psi }_1\left(\theta \right),x_2\left(\theta \right)={\psi }_2\left(\theta \right),x_3\left(\theta \right)={\psi }_3\left(\theta \right),\theta \in [-\tau ,0],$$ (2.4)

where the initial function $\psi =({\psi }_1,{\psi }_2,{\psi }_3)$ belongs to the Banach space $C=C([-\tau ,0],{\mathbb{R}}^3)$ of continuous functions mapping the interval $[-\tau ,0]$ into ${\mathbb{R}}^3$. For biological reasons, the initial functions are assumed as

$${\psi }_i\left(\theta \right)\ge 0,\theta \in [-\tau ,0],i=1,2,3.$$ (2.5)

3. Preliminaries

In this section, we have illustrated some basic results, such as existence and uniqueness of the solution and permanence of the system (2.2).

3.1. Existence and uniqueness of the solution

Theorem 3.1

System (2.2) with initial conditions (2.4) possesses a unique positive solution in the interval $[-\tau ,\infty )$ .

Proof

Since the right hand side of the system (2.2) is completely continuous and locally Lipschitzian on C, the solution (x ₁(t), x ₂(t), x ₃(t)) of system (2.2) with initial conditions (2.4) exists and is unique on [0, α), where $0<\alpha \le +\infty$ [72]. Now, from the first equation of system (2.2), we have

$$x_1\left(t\right)=x_1\left(0\right)\exp {\int }_0^t[r\left(s\right)-k\left(s\right)(x_1\left(s\right)+x_2\left(s\right))-a_1\left(s\right)x_3\left(s\right)-\beta \left(s\right)x_2\left(s\right)]ds>0,\forall t\ge 0.$$

Form the third equation of system (2.2), we have

$$x_3\left(t\right)=x_3\left(0\right)\exp {\int }_0^t[c_1\left(s\right)x_1\left(s\right)+c_2\left(s\right)x_2\left(s\right)-d\left(s\right)-b\left(s\right)x_3\left(s\right)]ds>0,\forall t\ge 0.$$

Next, we prove that x ₂(t) > 0, ∀ t ≥ 0. If not, then ∃ a t ₁ > 0, s.t. $x_2\left(t_1\right)=0$ and $x_2\left(t\right)\ge 0,\forall t\in [-\tau ,t_1]$. Furthermore,

$$\frac{d{x}_2\left(t\right)}{dt}\ge -a_1\left(t\right)x_2\left(t\right)x_3\left(t\right)-e\left(t\right)x_2\left(t\right),\forall t\in [0,t_1].$$

Then,

$$\begin{array}{ccc}& & x_2\left(t\right)\ge x_2\left(0\right)\exp {\int }_0^t[-a_1\left(s\right)x_3\left(s\right)-e\left(s\right)]ds>0,\forall t\in [0,t_1],\hfill \\ & & \Rightarrow x_2\left(t_1\right)\ge x_2\left(0\right)\exp {\int }_0^t[-a_1\left(s\right)x_3\left(s\right)-e\left(s\right)]ds>0,\hfill \end{array}$$

which contradicts our assumption. Hence, x ₂(t) > 0, ∀ t ≥ 0. □

3.2. Permanence of system (2.2)

Here, we discuss permanence of the system (2.2) with initial conditions (2.4), which demonstrates how the system will be uniformly persistent, i.e., the long-term survival of all components of the system (2.2) with initial conditions (2.4), under some conditions. Let $f^l={\inf }_{t\ge 0}f\left(t\right)$ and $f^u={\sup }_{t\ge 0}f\left(t\right),$ for a continuous and bounded function f(t) defined on the interval $[0,+\infty )$.

Definiton 3.1

System (2.2) is said to be uniformly persistent, if there are positive constants v_i and w_i, $i=1,2,3$ such that

$$\begin{array}{ccc}& & v_1\le \underset{t\to \infty }{\lim }\inf x_1\left(t\right)\le \underset{t\to \infty }{\lim }\sup x_1\left(t\right)\le w_1,\hfill \\ & & v_2\le \underset{t\to \infty }{\lim }\inf x_2\left(t\right)\le \underset{t\to \infty }{\lim }\sup x_2\left(t\right)\le w_1,\hfill \\ & & v_3\le \underset{t\to \infty }{\lim }\inf x_3\left(t\right)\le \underset{t\to \infty }{\lim }\sup x_3\left(t\right)\le w_3,\hfill \end{array}$$

hold for any solution (x ₁(t), x ₂(t), x ₃(t)) of system (2.2) with initial conditions (2.4). Here, v_i and w_i, $i=1,2,3$ are independent of initial conditions (2.4).

Lemma 3.1

Consider the following system [73] ,

$$\dot{x}=ax(t-\tau )-bx\left(t\right)-c{x}^2\left(t\right),$$

where a, b, c, τ > 0; x(t) > 0, for $-\tau \le t\le 0$ . Then, we have

$$\begin{array}{c}\hfill \underset{t\to \infty }{\lim }x\left(t\right)=\{\begin{array}{cc}\frac{a-b}{c}\hfill & a>b\hfill \\ 0\hfill & a<b.\hfill \end{array}\end{array}$$

Theorem 3.2

Let $X\left(t\right)=(x_1\left(t\right),x_2\left(t\right),x_3\left(t\right))$ be a solution of system (2.2) with initial conditions (2.4) . Suppose that system (2.2) satisfies the following condition,

$$M^{*}=\max \{\left(\frac{r^u}{k^l}\right),\left(\frac{{\beta }^u}{e^l}\right)\left(\frac{r^u}{k^l}\right)\}>\frac{d^l}{{(c_1+c_2)}^u},$$ (3.1)

then ∃ a T ₃ > 0 such that

$$x_1\left(t\right),x_2\left(t\right)<M_3,x_3\left(t\right)\le M_4,\forall t\ge T_3,$$ (3.2)

where M ₃ > M* and $M_4>\frac{{(c_1+c_2)}^u{M}^{*}-d^l}{b^l}.$

Proof

Let $M_1>\left(\frac{r^u}{k^l}\right).$ From the first equation of system (2.2), we have

$${\dot{x}}_1\left(t\right)\le x_1\left(t\right)[r\left(t\right)-k\left(t\right)x_1\left(t\right)]\le x_1\left(t\right)[r^u-k^l{x}_1\left(t\right)].$$

Therefore, if x ₁(0) ≤ M ₁, then x ₁(t) ≤ M ₁, ∀ t ≥ 0. If x ₁(0) > M ₁, and let $-{\alpha }_1=M_1(r^u-k^l{M}_1),$ α ₁ > 0, then ∃ an ϵ > 0, such that if t ∈ [0, ϵ), x ₁(t) > M ₁, and we have ${\dot{x}}_1\left(t\right)<-{\alpha }_1<0$. Therefore, ∃ a T ₁ > 0 such that x ₁(t) ≤ M ₁, ∀ t ≥ T ₁.

From the second equation of system (2.2), we obtain

$${\dot{x}}_2\left(t\right)\le {\beta }^u{M}_1{x}_2(t-\tau )-e^l{x}_2\left(t\right),t\ge T_1+\tau .$$

By Lemma 3.1, we conclude that

$$\exists \text{a}{T}_2\ge T_1+\tau \text{such}\text{that}{x}_2\left(t\right)\le M_2,\forall t\ge T_2,\text{where}{M}_2>\frac{{\beta }^u{M}_1}{e^l}.$$

M ₁ can be chosen sufficiently close to $\left(\frac{r^u}{k^l}\right).$ Hence, x ₁(t), x ₂(t) ≤ M ₃, where

$$M_3>M^{*}=\max \{\left(\frac{r^u}{k^l}\right),\left(\frac{r^u}{k^l}\right)\left(\frac{{\beta }^u}{e^l}\right)\},\forall t\ge T_2.$$

From the last equation of system (2.2), we have

$${\dot{x}}_3\left(t\right)\le x_3\left(t\right)[{(c_1+c_2)}^u{M}_3-d^l-b^l{x}_3\left(t\right)],\forall t\ge T_2.$$

Therefore, ∃ a T ₃ > 0 such that x ₃(t) ≤ M ₄ ∀ t > T ₃, where $M_4>\frac{{(c_1+c_2)}^u{M}^{*}-d^l}{b^l},$ since M ₃ can be chosen sufficiently close to M*. This completes the proof. □

Theorem 3.3

System (2.2) with initial conditions (2.4) is uniformly persistent if the following condition is satisfied,

$$\frac{d^l}{{(c_1+c_2)}^u}<M^{*}=\max \{\left(\frac{r^u}{k^l}\right),\left(\frac{r^u}{k^l}\right)\left(\frac{{\beta }^u}{e^l}\right)\}<\min \{\frac{b^l{r}^l+a_1^u{d}^l-\frac{k^u{d}^u{b}^l}{{(c_1+c_2)}^l}}{{(k+\beta )}^u{b}^l+a_1^u{(c_1+c_2)}^u},\frac{{\beta }^l(b^l{r}^l+a_1^u{d}^l)+a_2^u{d}^l{k}^u}{{\beta }^l\{{(k+\beta )}^u{b}^l+a_1^u{(c_1+c_2)}^u\}+k^u{a}_2^u{(c_1+c_2)}^u}\}.$$ (3.3)

Proof

Suppose $X\left(t\right)=(x_1\left(t\right),x_2\left(t\right),x_3\left(t\right))$ be a solution of the system (2.2) with initial conditions (2.4). Using Theorem 3.2, we have

$${\dot{x}}_1\left(t\right)\ge x_1\left(t\right)[r^l-\{{(k+\beta )}^u{M}_3+a_1^u{M}_4\}-k^u{x}_1\left(t\right)],\forall t\ge T_3.$$

If $r^l-\{{(k+\beta )}^u{M}_3+a_1^u{M}_4\}>0,$ then we can choose m ₁ such that

$$\begin{array}{ccc}& & 0<m_1<\frac{r^l-\{{(k+\beta )}^u{M}_3+a_1^u{M}_4\}}{k^u}\hfill \\ & & \Rightarrow r^l-\{{(k+\beta )}^u{M}_3+a_1^u{M}_4\}-k^u{m}_1>0.\hfill \end{array}$$ (3.4)

If x ₁(T ₃) ≥ m ₁, then x ₁(t) ≥ m ₁ ∀ t ≥ T ₃. If x ₁(T ₃) < m ₁, and let ${\mu }_1=x_1\left(T_3\right)[r^l-\{{(k+\beta )}^u{M}_3+a_1^u{M}_4\}-k^u{m}_1]>0,$ then ∃ an ϵ₁ > 0, such that x ₁(t) < m ₁, and ${\dot{x}}_1>{\mu }_1>0,\forall t\in [T_3,T_3+{ϵ}_1)$. Therefore,

$$\exists \text{a}{T}_4>T_3>0,\text{such}\text{that}{x}_1\left(t\right)\ge m_1\forall t\ge T_4.$$ (3.5)

From the second equation of system (2.2), we have

$$\begin{array}{ccc}\hfill {\dot{x}}_2\left(t\right)& \ge & {\beta }^l{m}_1{x}_2(t-\tau )-(a_2^u{M}_3+e^u)x_2\left(t\right),\hfill \\ & \ge & {\beta }^l{m}_1{x}_2(t-\tau )-{ϵ}_2{x}_2^2\left(t\right)-(a_2^u{M}_3+e^u)x_2\left(t\right),\forall t\ge T_4+\tau ,\hfill \end{array}$$

where ϵ₂ is any positive real number. If ${\beta }^l{m}_1>a_2^u{M}_3+e^u,$ then by Theorem 3.2, we conclude that

$$\exists \text{a}{T}_5\ge T_4+\tau \text{such}\text{that}{x}_2\left(t\right)\ge m_2,\forall t\ge T_5,$$ (3.6)

where $m_2<\frac{{\beta }^l{m}_1-(a_2^u{M}_3+e^u)}{{ϵ}_2}.$

Hence,

$$x_1\left(t\right),x_2\left(t\right)\ge m_3,\forall t\ge T_5,$$ (3.7)

where $m_3<m^{*}=\min \{m_1,m_2\}$.

From the third equation of system (2.2), we have

$${\dot{x}}_3\left(t\right)\ge x_3\left(t\right)[{(c_1+c_2)}^l{m}_3-d^u-b^u{x}_3\left(t\right)].$$

If ${(c_1+c_2)}^l{m}_3>d^u,$ then we can choose m ₄ such that $0<m_4<\frac{{(c_1+c_2)}^l{m}_3-d^u}{b^u}.$ If x ₃(T ₅) ≥ m ₄, then x ₃(t) ≥ m ₄, ∀ t ≥ T ₅. If x ₃(T ₅) < m ₄ and let ${\mu }_2=x_3\left(T_5\right)\{{(c_1+c_2)}^l{m}_3-d^u-m_4{b}^u\}>0,$ then ∃ an ϵ₃ > 0 such that x ₃(t) < m ₄ and ${\dot{x}}_3\left(t\right)>{\mu }_2>0,$ $\forall t\in [T_5,T_5+{ϵ}_3)$. Therefore, ∃ a T ₆ > T ₅ > 0 such that x ₃(t) ≥ m ₄ ∀ t > T ₆. From the above discussions, we conclude that ∃ a T ₆ > 0, such that every solution of system (2.2) with initial conditions (2.4) eventually enters and remains in the region

$$\Omega =\left\{(x_1,x_2,x_3)\right|m\le x_i\le M,i=1,2,3\},\forall t\ge T_6,$$

where $m=\min \{m_3,m_4\}$ and $M=\max \{M_3,M_4\}$. This completes the proof. □

4. Global asymptotic stability

Global asymptotic stability of solutions of system (2.2) is defined as follows.

Definiton 4.1

System (2.2) with initial conditions (2.4) is said to be globally asymptotically stable if for any two solutions (x ₁(t), x ₂(t), x ₃(t)) and (u ₁(t), u ₂(t), u ₃(t)), the following conditions are satisfied,

$$\underset{t\to \infty }{\lim }|x_1\left(t\right)-u_1\left(t\right)|=0,\underset{t\to \infty }{\lim }|x_2\left(t\right)-u_2\left(t\right)|=0,\underset{t\to \infty }{\lim }|x_3\left(t\right)-u_3\left(t\right)|=0.$$

Theorem 4.1

If there exist α ₁ > 0, α ₂ > 0 and α ₃ > 0 such that the functions B_i(t), $i=1,2,3$ are nonnegative on [0, ∞), and for any sequence of intervals ${\left\{[e_i,f_i]\right\}}_1^{\infty },$ $[e_i,f_i]\cap [e_j,f_j]=\varphi$ and $f_i-e_i=f_j-e_j>0,$ $\forall i,j=1,2,\dots$ and i ≠ j satisfying ${\sum }_{k=1}^{\infty }{\int }_{e_k}^{f_k}{B}_i\left(t\right)dt=\infty ,$ then the system (2.2) with initial conditions (2.4) is globally asymptotically stable. Here,

$$\begin{array}{ccc}& & B_1\left(t\right)={\alpha }_{1}k\left(t\right)-{\alpha }_{2}M\beta (t+\tau )-{\alpha }_3{c}_1\left(t\right),\hfill \\ & & B_2\left(t\right)={\alpha }_1(k\left(t\right)+\beta \left(t\right))+{\alpha }_2(m{a}_2\left(t\right)+e\left(t\right))-{\alpha }_{2}M\beta (t+\tau )-{\alpha }_3{c}_2\left(t\right),\hfill \\ & & B_3\left(t\right)={\alpha }_1{a}_1\left(t\right)+{\alpha }_{2}m{a}_2\left(t\right)+{\alpha }_{3}b\left(t\right),\hfill \end{array}$$ (4.1)

where m and M are the same as in Theorem 3.3 .

Proof

Let (x ₁(t), x ₂(t), x ₃(t)) and (u ₁(t), u ₂(t), u ₃(t)) be any two solutions of system (2.2) with initial conditions (2.4). Define

$$V_1\left(t\right)=|\ln x_1\left(t\right)-\ln u_1\left(t\right)|,V_2\left(t\right)=|x_2\left(t\right)-u_2\left(t\right)|,V_3\left(t\right)=|\ln x_3\left(t\right)-\ln u_3\left(t\right)|.$$

The right-upper derivatives of V ₁(t), V ₂(t) and V ₃(t) along the solutions of system (2.2) with initial conditions (2.4) are given by

$$\begin{array}{cc}\hfill D^{+}{V}_1\left(t\right)& =(\frac{{\dot{x}}_1\left(t\right)}{x_1\left(t\right)}-\frac{{\dot{u}}_1\left(t\right)}{u_1\left(t\right)})sgn(x_1\left(t\right)-u_1\left(t\right))\hfill \\ & \le -k\left(t\right)|x_1\left(t\right)-u_1\left(t\right)|-(k\left(t\right)+\beta \left(t\right))|x_2\left(t\right)-u_2\left(t\right)|-a_1\left(t\right)|x_3\left(t\right)-u_3\left(t\right)|,\hfill \end{array}$$ (4.2)

$$\begin{array}{cc}\hfill D^{+}{V}_2\left(t\right)& =({\dot{x}}_2\left(t\right)-{\dot{u}}_2\left(t\right))sgn(x_2\left(t\right)-u_2\left(t\right))\hfill \\ & \le \beta \left(t\right)\left\{x_2(t-\tau )\right|x_1(t-\tau )-u_1(t-\tau )|+u_1(t-\tau )|x_2(t-\tau )-u_2(t-\tau )\left|\right\}\hfill \\ & -a_2\left(t\right)\{x_3\left(t\right)|x_2\left(t\right)-u_2\left(t\right)|+u_2\left(t\right)|x_3\left(t\right)-u_3\left(t\right)\left|\right\}-e\left(t\right)|x_2\left(t\right)-u_2\left(t\right)|,\hfill \end{array}$$ (4.3)

$$\begin{array}{cc}\hfill D^{+}{V}_3\left(t\right)& =(\frac{{\dot{x}}_3\left(t\right)}{x_3\left(t\right)}-\frac{{\dot{u}}_3\left(t\right)}{u_3\left(t\right)})sgn(x_3\left(t\right)-u_3\left(t\right))\hfill \\ & \le -b\left(t\right)|x_3\left(t\right)-u_3\left(t\right)|+c_1\left(t\right)|x_1\left(t\right)-u_1\left(t\right)|+c_2\left(t\right)|x_2\left(t\right)-u_2\left(t\right)|.\hfill \end{array}$$ (4.4)

Define

$$V_{20}={\int }_{t-\tau }^t\beta (s+\tau )x_2\left(s\right)|x_1\left(s\right)-u_1\left(s\right)|ds+{\int }_{t-\tau }^t\beta (s+\tau )u_1\left(s\right)|x_2\left(s\right)-u_2\left(s\right)|ds.$$ (4.5)

Calculating the right-upper derivative of V ₂₀ along the solutions of system (2.2) with initial conditions (2.4), we get

$$\begin{array}{ccc}\hfill D^{+}{V}_{20}\left(t\right)& =& \beta (t+\tau )x_2\left(t\right)|x_1\left(t\right)-u_1\left(t\right)|-\beta \left(t\right)x_2(t-\tau )|x_1(t-\tau )-u_1(t-\tau )|\hfill \\ & & +\beta (t+\tau )u_1\left(t\right)|x_2\left(t\right)-u_2\left(t\right)|-\beta \left(t\right)u_1(t-\tau )|x_2(t-\tau )-u_2(t-\tau )|.\hfill \end{array}$$ (4.6)

Let

$$V\left(t\right)={\alpha }_1{V}_1\left(t\right)+{\alpha }_2(V_2\left(t\right)+V_{20})+{\alpha }_3{V}_3\left(t\right).$$

Using Eqs. (4.2)–(4.6), the right-upper derivative of V(t) is given by

$$D^{+}V\left(t\right)\le -B_1\left(t\right)|x_1\left(t\right)-u_1\left(t\right)|-B_2\left(t\right)|x_2\left(t\right)-u_2\left(t\right)|-B_3\left(t\right)|x_3\left(t\right)-u_3\left(t\right)|,\forall t\ge T_6,$$ (4.7)

where T ₆ is defined in Theorem 3.3 and B_i(t), $i=1,2,3$ are defined in (4.1).

Now, integrating (4.7) from T ₆ to t, we have

$${\int }_{T_6}^t\{B_1\left(t\right)|x_1\left(t\right)-u_1\left(t\right)|+B_2\left(t\right)|x_2\left(t\right)-u_2\left(t\right)|+B_3\left(t\right)|x_3\left(t\right)-u_3\left(t\right)\left|\right\}dt\le V\left(T_6\right)-V\left(t\right).$$ (4.8)

Implying,

$${\int }_{T_6}^t\{B_1\left(t\right)|x_1\left(t\right)-u_1\left(t\right)|+B_2\left(t\right)|x_2\left(t\right)-u_2\left(t\right)|+B_3\left(t\right)|x_3\left(t\right)-u_3\left(t\right)\left|\right\}dt<\infty .$$ (4.9)

By assumptions (4.1) about B_i(t), $i=1,2,3$ and the boundedness of (x ₁(t), x ₂(t), x ₃(t)) and (u ₁(t), u ₂(t), u ₃(t)) on [0, ∞), we obtain from system (2.2) that $|x_1\left(t\right)-u_1\left(t\right)|,$ $|x_2\left(t\right)-u_2\left(t\right)|$ and $|x_3\left(t\right)-u_3\left(t\right)|$ are bounded and uniformly continuous on [0, ∞). It follows from (4.9) that

$$\underset{t\to \infty }{\lim }|x_1\left(t\right)-u_1\left(t\right)|=0,\underset{t\to \infty }{\lim }|x_2\left(t\right)-u_2\left(t\right)|=0,\underset{t\to \infty }{\lim }|x_3\left(t\right)-u_3\left(t\right)|=0.$$

This shows that the system (2.2) with initial conditions (2.4) is globally asymptotically stable. This completes the proof. □

Corollary 4.1

System (2.2) with initial conditions (2.4) is globally asymptotically stable if there exist α_i > 0, $i=1,2,3$ satisfying the following conditions,

$$\begin{array}{ccc}& & \lim \underset{t\to \infty }{\inf }\{{\alpha }_{1}k\left(t\right)-{\alpha }_{2}M\beta (t+\tau )-{\alpha }_3{c}_1\left(t\right)\}>0,\hfill \\ & & \lim \underset{t\to \infty }{\inf }\{{\alpha }_1(k\left(t\right)+\beta \left(t\right))+{\alpha }_2(m{a}_2\left(t\right)+e\left(t\right))-{\alpha }_{2}M\beta (t+\tau )-{\alpha }_3{c}_2\left(t\right)\}>0,\hfill \\ & & \lim \underset{t\to \infty }{\inf }\{{\alpha }_1{a}_1\left(t\right)+{\alpha }_{2}m{a}_2\left(t\right)+{\alpha }_3{b}_3\left(t\right)\}>0.\hfill \end{array}$$

Assume that the system (2.2) is ω—periodic, i.e., all coefficients are ω—periodic functions, then the system has a positive ω - periodic solution if it is uniformly persistent [74]. Thus, we have the following corollary.

Corollary 4.2

If system (2.2) is ω—periodic and conditions in Theorems 3.3 and 4.1 are satisfied, then there exists a unique positive ω—periodic solution which is globally asymptotically stable.

5. Numerical simulations

Here, we perform the numerical simulations to investigate the dynamical behaviors of systems (2.1) and (2.2). We compare the dynamics of the nonautonomous and delayed nonautonomous systems with the autonomous counterparts. Our aim is to explore different dynamical behaviors, including chaos. For the nonautonomous systems (2.1) and (2.2), we consider that the rate parameters are time dependent. More precisely, we consider that most of the biological parameters depends on temperature. It is to be noted that the daily average temperature changes periodically throughout the year. Therefore, in the present investigation, we consider the parameters to be a sinusoidal function,

$$\begin{array}{ccc}& & r\left(t\right)=r+r_{11}\sin \left(\omega t\right),e\left(t\right)=e+e_{11}\sin \left(\omega t\right),d\left(t\right)=d+d_{11}\sin \left(\omega t\right),\hfill \\ & & k\left(t\right)=k+k_{11}\sin \left(\omega t\right),b\left(t\right)=b+b_{11}\sin \left(\omega t\right),\beta \left(t\right)=\beta +{\beta }_{11}\sin \left(\omega t\right),\hfill \\ & & a_1\left(t\right)=a_1+a_{11}\sin \left(\omega t\right),a_2\left(t\right)=a_2+a_{22}\sin \left(\omega t\right),c_1\left(t\right)=c_1+c_{11}\sin \left(\omega t\right),\hfill \\ & & c_2\left(t\right)=c_2+c_{22}\sin \left(\omega t\right),\hfill \end{array}$$ (5.1)

with period of 365 days. We have also considered the parameters in such a way that all the parameters are positive, continuous and bounded.

First, we study the behavior of autonomous system without time delay. We simulated the system (2.1) by assuming the system’s parameters to be independent of time. We choose a set of hypothetical but biologically feasible parameter values as,

$$r=1,e=0.1,d=0.1,k=1,b=0.2,\beta =0.8,a_1=0.6,a_2=0.5,c_1=0.2,c_2=0.2,$$ (5.2)

and

$$r_{11}=e_{11}=d_{11}=k_{11}=b_{11}={\beta }_{11}=a_{11}=a_{22}=c_{11}=c_{22}=0.$$

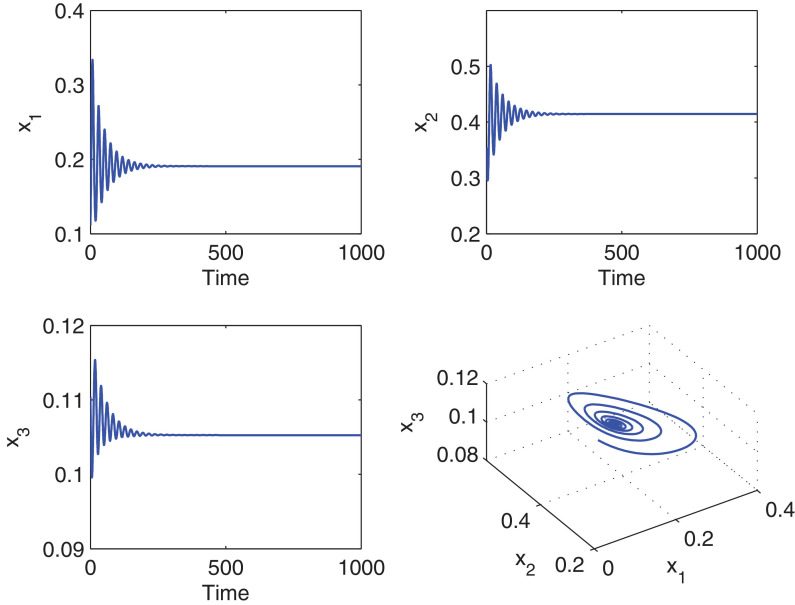
By assigning the seasonal forcing terms to be zero, we can get the corresponding autonomous system. Numerically, we compute the coexisting equilibrium point $E^{*}=(0.1908,0.4145,0.1053)$ and the eigenvalues of the Jacobian matrix of the autonomous system at the equilibrium E* are $-0.0955\pm 0.3340i$ and $-0.021$. Therefore, the interior equilibrium point of the autonomous system is asymptotically stable. We plot the solution trajectories in Fig. 1 and observe that the system is stable focus for the above parameter values.

Fig. 1.

Simulation results of the system (2.1) in the absence of seasonality and time delay. For the parameter values given by (5.1), system (2.1) shows stable focus. The first three figures are the time series for the susceptible prey, the infected prey and the predator, and the fourth figure is the 3D phase portrait of the stable interior of the system.

Next, we simulate the system (2.1) by assuming all the parameters to be affected by seasonality. To incorporate the periodic functional form of rate parameters, we consider these rate parameters to be a sinusoidal function with a period of one year ($\omega =2\pi /365$), and set

$$\begin{array}{ccc}& & r_{11}=0.01,e_{11}=0.01,d_{11}=0.01,k_{11}=0.6,b_{11}=0.01,\hfill \\ & & {\beta }_{11}=0.1,a_{11}=0.01,a_{22}=0.01,c_{11}=0.05,c_{22}=0.01,\hfill \end{array}$$ (5.3)

in (5.1). Therefore, the above time dependent parameters in (5.1) are bounded, positive periodic function. The solution trajectories of the nonautonomous system (2.1) are plotted in Fig. 2 . We observe that there exists a positive periodic solution. Thus, for the same set of the parameter values the nonautonomous system (2.1) exhibits positive periodic solution while the corresponding autonomous system shows stable focus.

Fig. 2.

Simulation results of the nonautonomous system without time delay (system (2.1)) for the parameter values given by (5.2) and (5.3). The figure shows that the nonautonomous system without delay exhibits positive periodic solutions for seasonally varying parameter values.

Further, numerically we study the effect of time delay on the stability behavior of the autonomous system. We plot the solution trajectories by fixing the value of time delay at $\tau =2$. The autonomous system with time delay shows stable focus for the parameter values given by (5.2), Fig. 3 . Next, we increase the value of time delay to $\tau =5$ and plot the solution trajectories. We observe that the autonomous system shows limit cycle behavior for the parameter values given by (5.2) and $\tau =5,$ Fig. 4 . Thus, to get a clear picture for the effect of time delay on the autonomous system, we draw the bifurcation diagram by varying the time delay in the interval (0, 15], where other parameter values are given by (5.2), Fig. 5 . From the figure, it is clear that by increasing the values of time delay, the autonomous system undergoes a Hopf-bifurcation and exhibits limit cycle oscillations. The critical value of time delay at which the stability behavior of the autonomous system changes is ${\tau }_c=3.1$. Therefore, below the threshold value of time delay, the delayed autonomous system shows stable dynamics, whereas above the threshold value, the system shows limit cycle oscillations.

Fig. 3.

Simulation results of the autonomous system at $\tau =2$ for the parameter values given by (5.2). In the absence of seasonal forcing, the system exhibits stable focus for the low values of time delay.

Fig. 4.

Simulation results of the autonomous system at $\tau =5$ for the parameter values given by (5.2). In the absence of seasonal forcing, the system exhibits limit cycle oscillations for higher values of time delay.

Fig. 5.

Bifurcation diagram of the autonomous system with respect to τ for the parameter values given by (5.2). In the absence of seasonal forcing, for gradual increase in the values of delay parameter, the system undergoes a Hopf-bifurcation and switches it’s stability from stable focus to limit cycle oscillation.

To investigate the combined effect of the incubation delay and the seasonal forcing, we draw the bifurcation diagram of the nonautonomous system (2.2) with respect to incubation delay by varying the values of τ in the interval (0, 15], where other parameter values are given by (5.2) and (5.3), Fig. 6 . It is clear from the figure that the nonautonomous system shows chaotic behavior through quasi-periodic oscillations for increasing the values of incubation delay. We obtain the threshold value of the time delay as ${\tau }^{*}=2.8$ at which the stability behavior of the nonautonomous system changes. Below the threshold value of incubation delay, the delayed nonautonomous system shows positive periodic solution with period 365 days. However, above the threshold value of the delay parameter, the nonautonomous system enters into the chaotic regime through quasi-periodic oscillations. The occurrence of chaotic oscillation may be explained through incommensurate limit cycles [2], [59]. It is noteworthy here that in the absence of delay, the nonautonomous system produces periodic solutions with a period of 365 days, whereas in the absence of seasonal forcing, the delayed autonomous system exhibits limit cycle oscillations with a period of 28 days approximately. Since these oscillations are not commensurate, i.e., the frequency of the first type of oscillation is not multiple of the frequency of the second type of oscillation, the combined system (delayed nonautonomous system) produces chaos [2], [59].

Fig. 6.

Bifurcation diagram of the delayed nonautonomous system with respect to τ for the parameter values given by (5.2) and (5.3). In the presence of seasonal forcing, the system enters into chaotic regime from positive periodic solutions for gradual increase in the delay parameter.

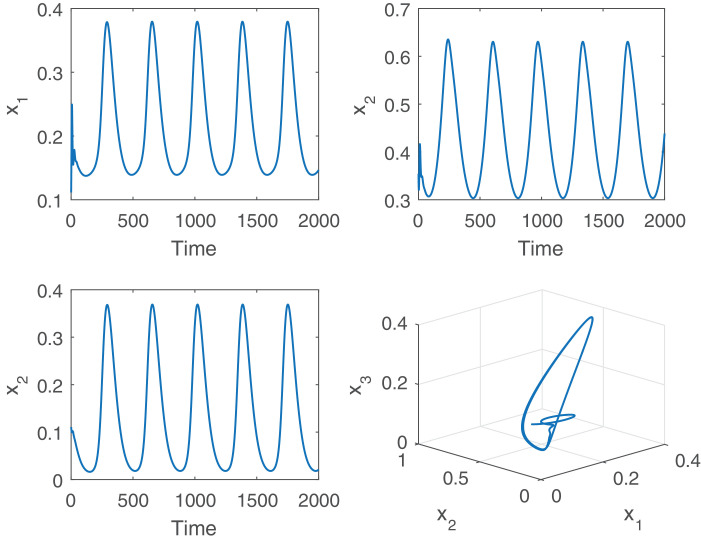
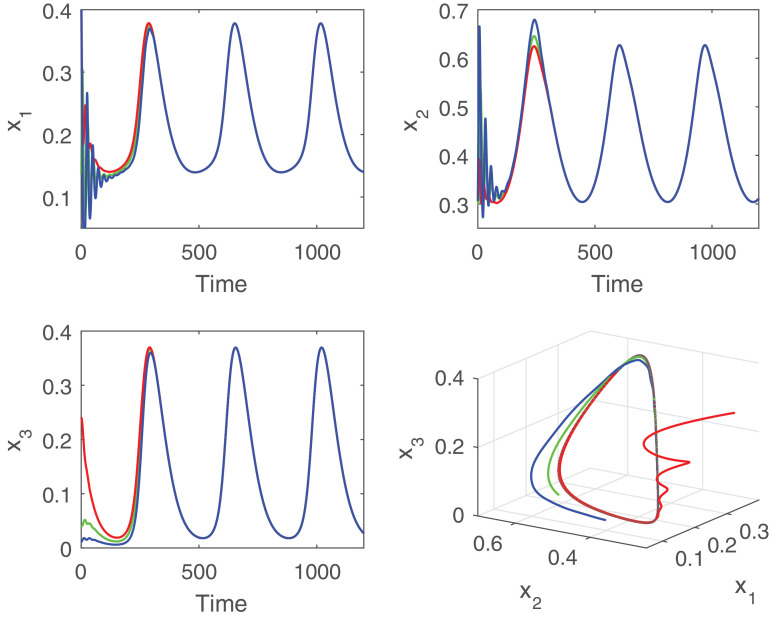
Further, we observe that the global stability of the positive periodic solution of the delayed nonautonomous system is affected by the delay parameter. For better understanding, we choose two values of the delay parameter from below and above of the threshold value ${\tau }^{*}=2.8$. We fix the value of incubation delay at $\tau =2$ and plot the solution trajectories initiated from three different initial values, Fig. 7 . It is apparent from the figure that all the periodic solutions initiating from three different initial values (0.41366, 0.3062, 0.0110), (0.41366, 0.3062, 0.2410) and (0.1366, 0.3062, 0.410) converge to a single periodic solution, i.e., the positive periodic solution is globally asymptotically stable. Therefore, Theorem 4.1 for the global asymptotic stability of the positive periodic solution of the nonautonomous system (2.2) is verified. Then, we choose $\tau =15$ (τ > τ*) and plot the solution trajectories of the nonautonomous system for the parameter values given by (5.2) and (5.3), Fig. 8 . It is evident from the figure that the system shows chaotic dynamics for $\tau =15$. Therefore, the global stability of the delayed nonautonomous system is affected due to enhancement of the delay parameter, whereas the persistence of the system is not affected by the magnitude of the delay.

Fig. 7.

Global stability of positive periodic solution for the system (2.2) at $\tau =2,$ when other parameter values are given by (5.2) and (5.3). Figure shows that solution trajectories starting from three different initial points (0.41366,0.3062,0.0110), (0.41366,0.3062,0.2410) and (0.1366,0.3062,0.410) ultimately converge to a unique positive periodic solution.

Fig. 8.

Simulation results for the nonautonomous system (2.2) at $\tau =15$ for the parameter values given by (5.2) and (5.3). In the presence of seasonal forcing, the system exhibits chaotic dynamics for larger values of time delay.

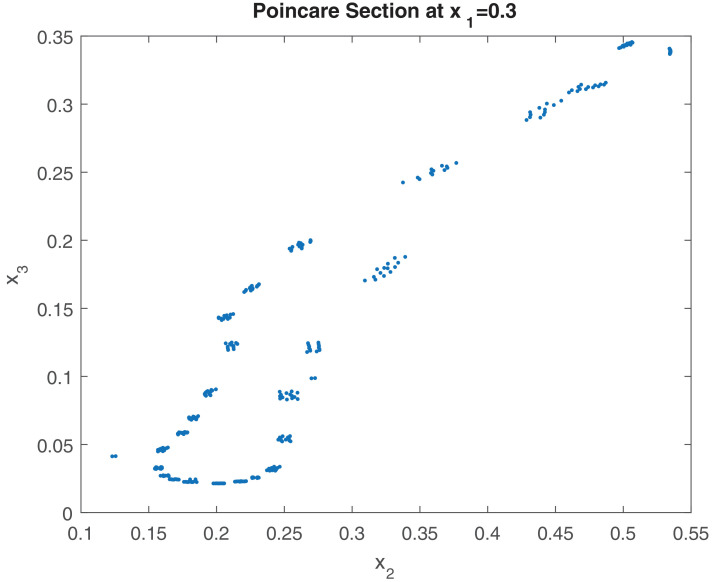
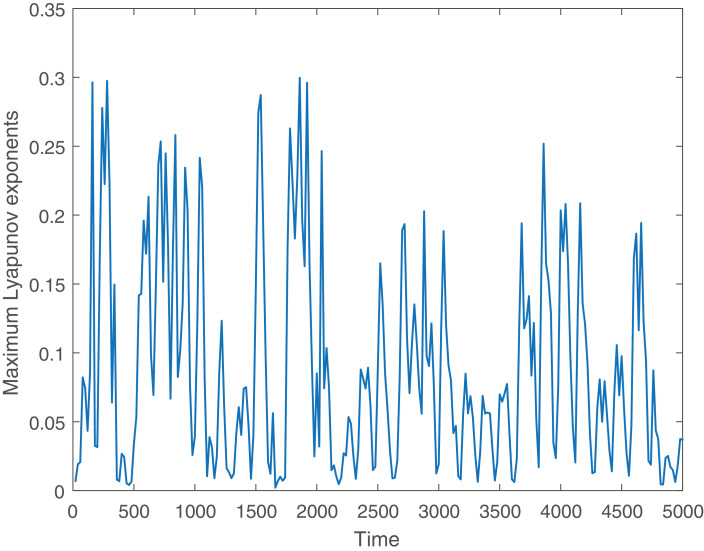
Further, we draw the Poincaré map of the system on $x_2-x_3$ plane ($x_1=0.30$) for $\tau =15$ (see Fig. 9 ). The scattered distribution of the sampling points implies the chaotic behavior of the system. We also draw the maximum Lyapunov exponent of the system (2.2) for $\tau =15,$ Fig. 10 . To draw the maximum Lyapunov exponent, we first simulate the delayed nonautonomous system (2.2), then considering the time series solutions of each component, we compute the Lyapunov exponents by using the algorithm of [75], [76]. In 1985, Wolf et al. [76] have proposed the algorithms that allow the estimation of non-negative Lyapunov exponents from an experimental time series. In Fig. 10, positive values of the maximum Lyapunov exponent indicate the chaotic regime of the system. It is to be noted here that the nonautonomous eco-epidemiological model can produce positive periodic solution with a period of 365 days. The delayed autonomous eco-epidemiological model produces limit cycle oscillations with a period of 28 days approximately. None of the nonautonomous and delay autonomous model produces chaotic oscillation. However, the combined eco-epidemiological model (delayed nonautonomous system) produces chaotic oscillation.

Fig. 9.

Figure shows the Poincare map of the nonautonomous system (2.2) in the x₂ - x₃ plane ($x_1=0.3$) for $\tau =15$. The scattered distribution of the sampling points indicates the chaotic dynamics of the system.

Fig. 10.

Figure shows the maximum Lyapunov exponent of the nonautonomous delayed system (2.2) for $\tau =15$. In the figure, positive values of the maximum Lyapunov exponent confirms the occurrence of chaotic oscillation.

6. Conclusion

In the past few decades, the emergence of infectious diseases among humans and animals remains the leading cause behind the mortality of individuals contradicting the paradigm that disease is not an important cause for the mortality of wildlife populations [77], [78]. Presence of infection among individuals regulates the size of population [79] and plays a leading factor for the extinction of species [80]. It is to be noted that the rate of disease transmission, and the other biological rate parameters depend on light intensity, temperature and rainfall. Therefore, such parameters are time dependent and their values follow the periodic (sinusoidal) function with lower bound greater than zero [21], [22], [44]. On the other hand, considering infection in prey/predator in the modeling process increases the dimension of the system and consequently, the possibility for the occurrence of chaotic dynamics increases. In general, almost every biological process has some delay effects. For example, incubation delay in disease transmission, gestation delay in predator, maturation delay, delay in defense mechanism, etc. Therefore, models with time delays are more realistic but are complicated in analyzing. Such systems can exhibit more biological as well as dynamical properties, which are not present in the corresponding non-delayed systems. Moreover, time delay can produce rich dynamics as increasing the values of time delay may produce oscillations in the system. A lot of studies showed the occurrence of limit cycle oscillations through a Hopf-bifurcation by varying the delay parameter [27], [81]. However, fewer studies are carried out for the delayed systems showing chaotic dynamics [47], [57]. In the present investigation, our aim is to extensively study the delay dynamics and explore how the system produces chaotic behavior due to presence of time delay and seasonality. We propose a nonautonomous predator-prey model by considering that a disease spreads among prey population and transmitted by direct contact only. We have incorporated a delay for the incubation period in the modeling process to make the system more realistic. Conditions for the permanence of the system are obtained analytically. The system is shown to be globally asymptotically stable under certain conditions. Analysis of the system showed that the time delay has no effect on the permanence of the system, but the global asymptotical stability of the positive periodic solution is affected due to increase in the time delay parameter.

The analytical findings are well supported by numerical simulations. We consider periodic function (sinusoidal function) with a period of one year to incorporate the seasonal patterns of all the rate parameters. We have also studied the dynamical behavior of the systems (2.1) and (2.2) by assuming the rate parameters to be independent of time. In the absence of time delay, the autonomous version of the system (2.1) shows stable dynamics, whereas the nonautonomous system (2.1) shows a unique positive periodic solution with a period of one year. Further, we have explored the effect of time delay on the nonautonomous system (2.2) and the corresponding autonomous system. We have observed that the autonomous system undergoes a Hopf-bifurcation through limit cycle oscillations, whereas the corresponding nonautonomous system showed chaotic dynamics for increasing the incubation delay. We have observed that delay and seasonal forcing have the synergism effect for producing chaotic oscillations. We have plotted the solution trajectories of the system (2.2) for three different initial values, when the incubation delay is fixed at $\tau =2,$ and observed that the solutions of the system converge to a unique periodic solution. This shows that for a range of the time delay, the positive periodic solution is globally asymptotically stable. However, if the incubation delay is increased above a threshold value, then the system (2.2) exhibits chaotic oscillations. Thus, we can conclude that the incubation delay together with seasonal forcing is responsible for the chaotic dynamics, which was absent in the autonomous system.

There are several environmental factors, such as sun light, temperature, rainfall, etc., which can induce seasonality in the interacting population dynamics [70]. For aquatic ecosystems, light and temperature induce seasonal forcing in the rate parameters. In such systems, growth rate of phytoplankton (photosynthesis) is light dependent and the growth rate of zooplankton is temperature dependent, whereas the vertical migration of zooplankton is light dependent [22]. On the other hand, in epidemiology/ecoepidemiology, some infectious diseases show the peak in monsoon, which depend on rainfall, whereas some infectious diseases show spring/autumn peak depending on the suitable temperature. Therefore, aquatic ecosystems such as phytoplankton-zooplankton or zooplankton-fish interactions can be modelled using the present modelling techniques, when the phytoplankton or zooplankton population is subjected to disease infection. Moreover, in terrestrial ecosystem, plant-herbivore, herbivore-carnivore, mesocarnivore-large carnivore interactions can also be modelled using delayed nonautonomous coupled equations if the prey population is infected. Therefore, outcomes of the present investigation are very important for understanding such complex dynamical systems and they have wide spread applications in conservation biology.