Deep Learning of Static and Dynamic Brain Functional Networks for Early MCI Detection

Abstract

While convolutional neural network (CNN) has been demonstrating powerful ability to learn hierarchical spatial features from medical images, it is still difficult to apply it directly to resting-state functional MRI (rs-fMRI) and the derived brain functional networks (BFNs). We propose a novel CNN framework to simultaneously learn embedded features from BFNs for brain disease diagnosis. Since BFNs can be built by considering both static and dynamic functional connectivity (FC), we first decompose rs-fMRI into multiple static BFNs with modified independent component analysis. Then, voxel-wise variability in dynamic FC is used to quantify BFN dynamics. A set of paired 3D images representing static/dynamic BFNs can be fed into 3D CNNs, from which we can hierarchically and simultaneously learn static/dynamic BFN features. As a result, dynamic BFN features can complement static BFN features and, at meantime, different BFNs can help each other towards a joint and better classification. We validate our method with a publicly accessible, large cohort of rs-fMRI dataset in earlystage mild cognitive impairment (eMCI) diagnosis, which is one of the most challenging problems to the clinicians. By comparing with a conventional method, our method shows significant diagnostic performance improvement by almost 10%. This result demonstrates the effectiveness of deep learning in preclinical Alzheimer’s disease diagnosis, based on the complex and highdimensional voxel-wise spatiotemporal patterns of the resting-state brain functional connectomics. The framework provides a new but intuitive way to fully exploit deeply embedded diagnostic features from rs-fMRI for better individualized diagnosis of various neurological diseases.

I. Introduction

Alzheimer’s Disease (AD) is a serious neurological disease that is characterized by slowly progressive memory loss and cognitive deficits, constituting the most common form of dementia in the elderly people and becoming a worldwide health issue [1]. As AD is irreversible and incurable disease, detecting AD as early (e.g., at its preclinical stage, mild cognitive impairment: MCI) as possible is of great clinical importance for exerting possible interventions to delay its progression [2]. In recent years, increasing efforts have moved the frontline to possibly identifying MCI at its early stage, i.e., early MCI (eMCI), earning more precious time to help reduce the high conversion rate [2]. As visible structural changes in magnetic resonance imaging (MRI) of the eMCI brains could be little, many eMCI studies have adopted resting-state functional MRI (rs-fMRI) to investigate early brain function changes in eMCI patients [3–11].

The rs-fMRI is an in vivo brain functional imaging technique which measures blood oxygen level-dependent (BOLD) signals when scanning subjects in natural rest without any explicit task engagement [4]. Based on rs-fMRI, functional connectivity (FC) between distant brain regions can be measured based on their temporally synchronized BOLD signals to generate whole-brain functional networks (BFNs) or brain “functional connectomics” [4].

A handful pioneering studies have been focusing on the FC changes in the BFNs in eMCI subjects by carrying out group-level statistic comparisons based on either network properties or simple regional pair-wise FCs [3]–[5]. While promising, the highly-complex spatial patterns in the BFNs are not fully considered by these mass-univariate analyses, and such information can be quite essential for individualized eMCI diagnosis. Furthermore, recent advances have consistently demonstrated the existence of rich diagnostic information in the temporal variation of the BFNs, namely, dynamic BFNs (dBFNs), which could underpin complex, adaptive, high-level cognitive functions [6]–[11]. The dBFNs could highly supplement the traditional static BFNs (sBFNs) that assume brain FC is not changing along the entire scanning time and, when jointly using both dBFNs and sBFNs, one can potentially boost diagnostic accuracy of brain diseases, including MCI [6]–[9] and even for eMCI [7]2013[11].

With BFN features, machine learning can be of great help for detecting disease-related abnormal patterns and increasing accuracy for individualized MCI diagnosis. Vast majority of these studies have used simple but very effective classifiers, such as support vector machine (SVM) [12], [13]. However, these classifiers might face problem when dealing with the highly-complex spatiotemporal connectomics information and lead to unsatisfactory eMCI diagnostic accuracy, partially due to more subtle changes in the BFNs compared to the late MCI.

Recently, deep learning has contributed more and more in the medicine field, benefited from its effectiveness in identifying deeply embedded, high-level features from the medical images. Among many deep learning algorithms, the convolutional neural network (CNN) [14] is one of the most popular and effective approaches that have been utilized widely for image segmentation [15], detection [16], and classification [9], [17]–[25]. We and other groups have utilized CNNs to help diagnose AD [20], [21] and MCI [22], [23] based on 3D structural MRI as a straightforward extension of CNNs from its ability in encoding 2D/3D natural images. However, design of a CNN model for eMCI diagnosis based on 4D rs-fMRI, or more specifically, based on highly complex spatiotemporal pattern of the sBFNs and dBFNs, is not an easy problem. This could be because 1) rs-fMRI and the derived BFNs have higher level of noise compared to the structural MRI [26]; 2) BFNs are sitting in a manifold when represented by adjacency matrices [27], making it difficult to define a “local pattern” for convolutional operation; 3) The temporal pattern of dBFNs cannot be simply learned, as different subjects have different temporal processes (not phase-locked) due to unconstraint resting state.

In this pioneering field, only a handful studies are trying to solve these problems [9], [10], [28]–[33]. To model the patterns in the FC adjacency matrix, most of the studies adopted fully connected (deep) neural networks or autoencoder proceeded by a vectorization of the whole-brain FC adjacency matrix [10], [28], [29]. However, such a brute-force vectorization could destroy the inherent spatial pattern information in the BFNs, making it less effective for classification. A few proof-of-concept studies proposed various (deep) graph CNNs with various specially-designed convolutional kernels, with which network structure/topology was integrated into deep convolutional learning [30]. Other studies adopted the recurrent neural network [31], gated recurrent unit [32], or long short-memory network [33] to learn directly from the temporal dynamics in rs-fMRI (so-called “deep chronnectome learning”). Specifically, in our recent work [9], we were trying to jointly and hierarchically learn the deeply embedded spatiotemporal patterns of the time-varying BFNs for MCI diagnosis by using a weighted correlation kernel. While these ideas have shed light on the field, they still need further validation due to the complicated model; also, the interpretation to the specially-designed kernels requires more works.

Different from the above methods, we recently proposed an intuitive solution that can naturally make use of the convenience and advantages of the 3D CNNs for eMCI classification [34]. This method was inspired by the success of 3D CNNs in analyzing natural and medical images [17]–[25] as well as the fact that similar 3D component maps can be generated as representations of sBFNs by using spatially independent component analysis (ICA) on rs-fMRI [35]. ICA is a major BFN extraction method in rs-fMRI studies, which discovers latent independent sources (usually represented by a set of 3D brain maps and their corresponding time series) in a datadriven manner [35]. The 3D brain maps are often regarded as sBFNs, with the value at each voxel representing the FC within a particular functional system that mediates certain brain functions, thus carrying rich spatial information. Traditional ICA studies use mass univariate voxel-wise analysis by comparing the FC values between eMCI and normal control (NC) groups, with the results indicating possible effect of high-level cognitive function-related BFNs in eMCI [3], [4]. Despite the ability of identifying small regions with potential diagnostic values [3], [4], the conventional approaches are insufficient to separate individual eMCI subjects from the healthy elderly subjects. From the dBFN point of view, the seed-based correlation with a sliding window strategy can easily generate a set of time-varying BFNs; their voxel-wise temporal variability could be regarded as dBFN in forms of 3D maps, providing additional temporal information of the BFNs.

In this paper, we propose a novel unified framework by using 3D CNNs to extract deep embedded features from both static and dynamic BFNs, without sacrificing rich spatial information of the BFNs. This further extends our preliminary idea presented in [34] that used only sBFNs. The extended method features the following advantages: 1) the deep embedded features can be well exploit in consideration of the subtle but complex (spatial and temporal) changes in each BFN in eMCI; 2) the inherent systemic level interactions among multiple BFNs can be jointly learned; and 3) the rich temporal information contained in the voxel-wise dBFNs could supplement sBFNs to further improve eMCI classification. We demonstrate the effectiveness of our framework in a challenging eMCI diagnosis problem using a rigorously collected, publicly accessible, multisite Alzheimer’s Disease Neuroimaging Initiative 2 (ADNI2)¹ dataset.

II. Materials and Methods

A. Dataset and Preprocessing

We used raw rs-fMRI data from 49 eMCI subjects (20M/29F, mean age 72.12 ± 7.22 yrs.) and 48 age-, gendermatched NC subjects (20M/28F, mean age 75.50 ± 6.81 yrs.) from the ADNI2 dataset as of September 2016. Note that, multiple rs-fMRI scans were longitudinally acquired (3.62 ± 1.99 scans per subject) for most of the subjects. We used all the available data as long as they corresponded to stable eMCI or NC status to increase sample size and better train the model. We did not include late MCI data but only eMCI in ADNI2, because the BFNs from the eMCIs are anticipated to be less affected due to the earlier stage of disease progression and, therefore, eMCI diagnosis is a more challenging task where deep learning may show its advantage.

Thus, we finally used a total of 351 samples (172 and 179 for NCs and eMCIs, respectively). The data are all acquired by 3T Philips scanners at multiple sites with a rigorous quality control to reduce the site effect. The rs-fMRI parameters are: TR = 3,000 ms, TE = 30 ms, voxel size = 3 × 3 × 3.3 mm³, the number of slices = 48, flip angle = 80^◦, and the number of volumes = 140.

We preprocessed the data using a widely-adopted DPARSF toolbox² with the pipeline used elsewhere [6], [7]. The first volumes acquired during the first 9 s were discarded to ensure magnetization equilibrium and the remaining volumes were head motion corrected, spatially normalized, spatially resampled (voxel resolution = 3 × 3 × 3 mm³), smoothed and band-pass filtered. Nuisance signals, including the head motion parameters, mean white matter, and cerebrospinal fluid signals, were regressed out to further remove the noise and artifacts. Framewise displacement (i.e., micro-head motion) was considered by removing the data with too many volumes that had framewise displacement > 0.5 mm.

B. Method Overview

CNN model is suitable to handle 3D medical images. Inspired by previous ICA studies where a set of 3D maps (BFNs) can be generated and used to detect disease-related biomarkers [3]–[5], [36], [37], we propose to use multi-channel CNNs to simultaneously learn spatial features from multiple BFNs. Considering the substantial contribution of dynamic FC to disease classification, we also propose to combine sBFN learning and dBFN learning into a unified framework (Fig. 1). It is divided into two parts: 1) “paired” (both static and dynamic version of a certain BFN) BFNs extraction, and 2) CNN-based hierarchical spatial feature learning. We use sdBFNs to refer a pair of sBFN and dBFN from now on. We construct a single 3D CNN by concatenating sBFN and dBFN as multi-channel input, namely, single sdBFNbased CNN (sdSB-CNN), to let sBFN and its corresponding dBFN support each other for diagnosis. The high-level features from the deep layer of each sdSB-CNN are then concatenated to form a merged, multiple sdBFNs-based 3D CNN (sdMB-CNN). This framework is able to integrate high-level features from each sdSB-CNN and jointly make better decision based on multiple BFNs that could be affected by the disease. More details are provided below.

Fig. 1.

An illustration of the proposed deep learning framework based on multiple paired static and dynamic brain functional networks (sdMB-CNN) extracted from rs-fMRI for brain disease diagnosis. K BFNs can be jointly used in this framework. A robust independent component analysis (ICA) algorithm is used to extract static BFNs (sBFN). Dynamic BFNs (dBFN) from the same functional systems are derived based on a well-adopted sliding-window seed-based functional connectivity (FC) approach with the seeds defined according to the ICA results. The paired sBFN and dBFN (sdBFNs) are concatenated as multi-channel input and then fed to the 3D CNN (sdSB-CNN). The proposed sdMB-CNN consists of multiple sdSB-CNNs by fusing the high-level features derived from each sdSB-CNN.

C. Static and Dynamic BFNs Extraction

The key of our method is the reliable detection of groupconsistent 3D BFN maps with less noise from the commonly noisy rs-fMRI data. To achieve this, we first use a modified version of individual-level ICA to extract multiple sBFNs from the rs-fMRI data, with predefined sBFN templates as a spatial prior. Compared to the traditional group-level ICA, such a method could ensure the rs-fMRI decomposition group consistent and less affected by noise. For capturing BFNs’ dynamics, we use a previously-proved consistent and reliable method, i.e., seed-based correlation with sliding window [6]– [11], with the seeds put into the BFNs. We then calculate voxel-wise temporal variability in dynamic FC and generate dBFN maps corresponding to the sBFNs.

1). Group Information Guided ICA-Based sBFN Extraction

We adopt Group Information Guided ICA (GIG-ICA) [38] to the entire rs-fMRI data of all subjects. As an individual ICA method, GIG-ICA decomposes 4D rs-fMRI data from each subject into a set of subject-specific 3D spatial maps, or components, without losing component correspondence across all subjects. This is achieved by providing group-level components as guidance to decompose individual data with a multiobjective optimization strategy. Compared to the conventional group-level ICA used in FSL [39] or GIFT [40], which strongly assumes that all subjects have the same components, GIG-ICA can drive subject-specific BFNs with stronger independence and better spatial correspondence across subjects, achieving higher spatial/temporal accuracy regarding BFN detection [38], [41]. In this way, individually unique BFN information can be better preserved, which is essential for the subsequent individual diagnosis. Another advantage is that GIG-ICA explicitly uses spatial prior from the provided BFN templates to reduce strong effect contributed by the extensive noise in rs-fMRI data. Therefore, more robust BFNs with less noise can be generated for each individual, and each BFN can be regarded as a voxel-wise spatial pattern of a certain brain functional system mediating specific cognitive function(s) [35].

We use the publicly available group ICA results³ that consist of 25 large-scale components generated with nearly a thousand of the Human Connectome Project (HCP) data [42]. They were obtained by means of standard group-level ICA with 812 healthy adult subjects. From the 25 components, we use six components (Fig. 2) that are associated with the higher-order cognitive functions [3], [4], [35], [43] because AD pathology could target more at the high-level cognitive functions in early stage. The six BFNs are the default mode networks (DMN), left and right fronto-parietal networks (FPN1&2), two attention networks (AN1&2), and executive control networks (ECN) [3], [4], [35], [43]. Note that there are different nomenclatures to them in the literature,⁴ but these six networks are regarded as high-level cognitive function related [3], [4], [35], [43]. By applying GIG-ICA with the group ICA templates to the preprocessed rs-fMRI data, we extract six individual-level BFNs for each subject from ADNI2 dataset. Note that, the HCP template just served as a prior information to the GIG-ICA to obtain individual BFNs with a better signal-to-noise ratio and a good correspondence across subjects. In each BFN, each voxel carries a value representing the FC in a certain functional network. Of note, ICA decomposes rs-fMRI data into a set of components (paired spatial maps and associated time series), we did not use the temporal information from the time series. The other components are either BFNs of no interest to us or the artifacts-related components were not used, such as sensorimotor network and a component mainly covering the white matter, as including them will make the model too complex to be correctly estimated. All the sBFNs were not thresholded; therefore, all spatial information is well preserved.

Fig. 2.

The z-maps of six selected group-level components (green) and their seed location (red) related to the high-level cognitive functions: (A) default mode network (DMN), (B, C) fronto-parietal networks (FPN1&2), (D, E) attention networks (AN1&2), and (F) executive control network (ECN), from the group ICA results provided by Human Connectome Project (HCP). Representative slices are shown for each component by using MRIcron⁵. x (left/right), y (anterior/posterior), and z (superior/inferior) denote their seed positions in the standard Montreal Neurological Institute (MNI) coordination system. A threshold of z > 3 is applied to each map for the visualization purpose.

2). Sliding-Window Seed Correlation-Based dBFN Extraction

To extract multiple dBFNs and make them easy to learn with a similar 3D-CNN framework, we borrow the idea of calculating FC dynamics using temporal variability (i.e., standard deviation) as effective diagnostic features in many previous dynamic FC studies [6]–[11]. First, we divide the whole time-range preprocessed rs-fMRI data into multiple overlapping temporal segments by means of sliding window (length = 30 time points or 90 s, stride = 20% window length, i.e., 17 time points). We then construct seed-based FC maps for each temporal segment and each selected BFN, respectively. The seed region of each BFN is centered at the peak voxel of the group ICA templates with a radius of 5 mm (Fig. 2). FC between the seed region and each other voxel in the brain is measured by Pearson’s correlation coefficient at each temporal segment [4]. Next, we calculate temporal variability of time-varying FC by means of standard deviation at each voxel across all sliding windows, which generates a 3D FC temporal variability map, termed dBFN, for each of the six BFNs.

With multiple sdBFNs for each subject (i.e., for all the six extracted functional networks), we then construct 3D CNNs to learn the sophisticated embedded spatial patterns from the sBFNs and dBFNs to make diagnosis. Of note, the term “dBFN” represents the temporal variation of BFNs. There are other metrics for characterizing BFN dynamics, such as dwelling time and transition probability between different statuses identified from the time-varying BFNs [44]; however, this summary index loses the voxel-wise information. Another method that calculates co-activation maps based on the raw rs-fMRI data can also generate a series of 3D maps, representing different brain statuses [45]; these resultant 3D maps can be easily implemented with our framework.

D. CNN-Based Spatial Feature Learning

We first construct each sdSB-CNN (paired static and dynamic BFN maps) to learn spatial features of each functional network. After constructing multiple sdSB-CNNs respectively for the six functional networks, we combine them by concatenating the last fully-connected layers of each sdSB-CNN to integrate discriminative high-level features of each functional network and form a unified sdMB-CNN (CNN based on multiple paired static and dynamic BFNs) framework to make a joint eMCI diagnosis. Fig. 3 illustrates the architecture of the sdMB-CNN. In the training stage, each sdSB-CNN is trained respectively. Then, their overall weights are refined by adopting the learned weights of sdSB-CNNs as initial weights.

Fig. 3.

An illustration for the structure of the proposed sdMB-CNN. Paired static and dynamic BFNs (sdBFN) of each selected component are fed to each single 3D CNN (sdSB-CNN) as multi-channel input, respectively. Each sdSB-CNN consists of three pairs of convolutional and pooling layers, two fully connected layers, and an output layer. The trained multiple sdSB-CNNs are merged by concatenating the last fully connected layers of each sdSB-CNN and adding an additional fully connected layer and a final output layer.

The details of the model are provided as below.

1). Single-sdBFN-Based CNN (sdSB-CNN) Construction

Each sdBFN is regarded as a multi-channel input. That is, information from the sBFN and the dBFN is fed to the model as two different channels, making them directly interact with each other since the beginning stage, i.e., in the 1^st convolutional layer. This is motivated by the previous finding of certain relationship existing between static FC and dynamic FC, e.g., the stronger the static FC is, the weaker FC dynamics is [46]. Meanwhile, the earlier they merge, the fewer model parameters are required. To reduce computational complexity, we use “cropped” 3D BFN maps in a dimension of 48 × 60 × 48 for each of them by excluding unnecessary background voxels from the original 3D BFN maps. The input is convolved by a series of three convolutional layers with Rectified Linear Unit (ReLU) activation. Each convolutional layer (kernel size = 3 × 3 × 3, stride = 1, padding = 1) is followed by a max-pooling layer (kernel size = 2 × 2 × 2, stride = 2) to down-sample the feature maps generated from the previous convolutional layers. The last feature maps are fully connected with two fully connected layers with 128 and 64 nodes and an output layer with 2 nodes for generating binary class labels that are used for back-propagation-based model learning. A softmax function is applied to the output units to predict the probability of an input belonging to NC or eMCI.

2). Multiple-sdBFN-Based CNN (sdMB-CNN) Construction

The last fully connected layers of each sdSB-CNN are concatenated [17], and then a fully connected layer with 64 nodes is added to merge the high-level features of each sdSB-CNN together and make them support each other. An output layer with a softmax function is connected to the top of the model for the final decision-making. The learned weights of each sdSB-CNN are adopted as the initial weights of sdMB-CNN, and then all the weights are refined together during the sdMB-CNN learning. With well-initialized weights, our model can be learned more robustly [47].

3). Implementation

Both the sdSB-CNN and sdMB-CNN models are implemented based on Caffe [48] with a single GPU (i.e., NVIDIA GTX TITAN 12GB). The network is optimized by stochastic gradient descent algorithm [49] with a momentum coefficient of 0.9 and the learning rate of 10⁻⁵. The weight updates are performed in mini-batches of 10 samples per batch.

III. Experiments and Results

A. Experimental Settings

To evaluate whether including multiple BFNs can help better diagnose, we compare the multiple BFNs-based classifications with different single BFN-based classifications, each of which makes diagnostic decision based only on one of the six BFNs. To validate the effectiveness of diagnosis using BFN dynamics as additional features, all the competing and the proposed methods are tested with two versions: 1) using static BFN(s) only and 2) using paired static and dynamic BFN(s) together. For clarity, we refer static BFN(s)-based method as SB-CNN and MB-CNN to differentiate them from the paired BFN(s)-based methods (sdSB-CNN and sdMB-CNN).

To see whether deep learning outperform traditional machine learning from the BFNs, we also compare our method with a conventional machine learning-based method, i.e., recursive feature elimination-based SVM [50]. Same as the proposed method, the competing method is also applied to both cases: SB-SVM and MB-SVM for using static BFN(s) only, as well as sdSB-SVM and sdMB-SVM for using both static and dynamic BFN(s).

Furthermore, we implement functional connectivity matrixbased graph CNN [51], [52]. In this method, we first parcellate brain regions into 116 regions of interest (ROIs) based on the Automated Anatomical Labeling (AAL) template, and extract mean time series from each ROI. We then calculate Fisher ztransformed Pearson correlation coefficients between the mean time series of each ROI to obtain a functional connectivity matrix. We use the functional connectivity matrix as weighted adjacency matrix of graph and used each row/column vector of the matrix as features of each vertex [52]. To learn embedded features of the graph, we construct graph CNN with two convolutional layers with 16 graph kernels and two fully connected layers with 128 and 64 nodes, respectively.

Finally, to verify superiority of the proposed CNN model that first separately trains high-level features of each BFN and then combines them for a subsequent joint training, we additionally implement a more direct and intuitive CNN model (direct MB-CNN), which uses all the BFNs as a multi-channel input (refer to Supplementary Fig. 2). The main difference between these two models is that the MB-CNN combines high-level spatial features of the BFNs while the direct MB-CNN combines low-level spatial features of the BFNs.

To evaluate each method, we adopt a 5-fold cross-validation strategy respecting independent subjects, i.e., we first randomly divided overall subjects into 5-folds and then used scans of subjects in 4-folds for model training while using scans of subjects in the rest fold for model testing iteratively. We performed every experiment with five repetitions, each of which has different combinations of training and testing samples. Of note, several subjects have multiple scans longitudinally; for training, all the scans from the same training subjects are included for better training. For the testing subjects, only their baseline scan is used for generating the testing result, mimicking the real application scenario, where only baseline data is collected, months or years before any follow-up scans.

B. Performance Evaluation

Diagnostic performance is computed by the quantitative metrics for comprehensive performance evaluation; accuracy (ACC), sensitivity (SEN), specificity (SPC), and positive and negative predictive value (PPV&NPV).

Table 1 shows the diagnostic performance of the proposed and competing methods when all the methods only use sBFNs as input. MB-CNN shows the best performance with 73.85% accuracy, which significantly improves the performance of the MB-SVM by 8.30% (p < 0.05, Friedman test [53]) and the graph CNN by 8.40% (p < 0.05). In the comparison between the proposed MB-CNN and direct MB-CNN, the proposed method shows improved accuracy by 2.61% (p = 0.07) over the direct MB-CNN. Note that, as ICA extracts spatially independent components, the low-level spatial features of BFNs are not quite overlapped to each other and they might not help each other well in the direct MB-CNN.

TABLE I.

Performance comparison of the proposed and competing methods by only using static BFNs (sBFNs).

Method	BFN	ACC (%)	SEN (%)	SPC (%)	PPV (%)	NPV (%)
Graph CNN	-	65.45	65.11	65.73	65.93	65.24
SB-SVM	DMN	63.63	66.93	60.09	63.40	64.47
	FPN1	59.12	59.96	58.18	59.48	56.68
	FPN2	62.04	62.31	61.56	63.04	61.74
	AN1	55.40	55.38	55.38	55.88	54.96
	AN2	55.80	55.51	55.96	56.65	54.96
	ECN	56.07	58.40	53.64	56.51	55.65
MB-SVM	DMN&FPNs	64.27	64.31	64.04	64.72	64.13
	All	65.55	65.38	65.69	66.25	65.17
SB-CNN	DMN	70.11	71.96	68.36	70.03	70.86
	FPN1	69.45	69.73	69.07	69.75	69.11
	FPN2	69.04	69.33	68.67	69.33	68.67
	AN1	68.02	69.42	66.53	68.33	67.94
	AN2	66.96	68.58	65.29	67.06	67.03
	ECN	67.19	67.64	66.62	67.65	66.96
Direct MB-CNN	All	71.24	71.51	71.11	72.12	71.58
MB-CNN	DMN&FPNs	73.03	72.67	73.42	73.70	73.35
	All	73.85	73.91	73.69	74.38	73.79

SB-SVMs and SB-CNNs are constructed for each BFN, respectively; the MB-SVM, direct MB-CNN, and MB-CNN methods use all the six BFNs (DMN: default mode network; FPN1&2: two fronto-parietal networks; AN1&2: two attention networks; ECN: executive control network). In addition, the models with three BFNs (DMN, FPN1&2 (FPNs)) are also listed for comparisons. Graph CNN uses Regions of Interest (ROI)-based functional connectivity.

Compared to different SB-CNNs constructed by using each sBFN, respectively, MB-CNN significantly improved the accuracy (3.74–6.89%, p < 0.05). The proposed MB-CNN also shows the best performance in terms of other measurements.

Interestingly, result comparisons among different SB-CNNs show that DMN, FPN1, and FPN2 have slightly better performance (1.02–3.15%, p = 0.02–0.23) compared to other BFNs. Therefore, we also constructed SVM and CNN models using these three major networks (DMN, FPN1&2 (FPNs)). The results are quite similar compared to those from MB-SVM and MB-CNN using all the six networks, with only a small performance increase if using all the six BFNs (~1%). According to the results, it is likely that the three BFNs could play more major roles in diagnosing eMCI than the rest of the BFNs.

Table 2 shows diagnostic performance of the proposed and competing methods, both of which used sdBFNs (including both static and dynamic BFNs) as inputs. Our proposed sdMB-CNN achieved the best accuracy of 76.07%, which significantly outperformed sdMB-SVM by 7.46% (p < 0.05). The receiver operating characteristic (ROC) curves and area under the curve (AUC) for MB-SVM, sdMB-SVM, MB-CNN, and sdMB-CNN are provided in Fig. 3 of Supplementary Materials.

TABLE II.

Performance comparison of the proposed and competing methods by using paired static and dynamic BFNs (sdBFNs).

Method	BFN	ACC (%)	SEN (%)	SPC (%)	PPV (%)	NPV (%)
sdSB-SVM	DMN	65.94	66.00	65.82	66.19	66.03
	FPN1	63.66	63.60	63.60	64.23	63.24
	FPN2	61.81	63.38	60.36	62.28	61.74
	AN1	56.17	53.78	58.53	57.15	55.33
	AN2	58.02	60.67	55.11	58.23	58.02
	ECN	56.29	58.58	53.64	56.07	56.34
sdMB-SVM	DMN&FPNs	66.21	68.09	64.00	66.12	66.86
	All	68.61	68.09	69.07	69.28	67.99
sdSB-CNN	DMN	73.17	73.91	72.44	73.70	73.03
	FPN1	72.80	73.07	72.44	73.30	72.86
	FPN2	71.53	71.07	72.13	72.51	71.62
	AN1	70.27	70.98	69.42	70.59	70.64
	AN2	69.08	68.27	70.00	70.69	68.48
	ECN	69.72	73.78	65.42	68.94	71.95
sdMB-CNN	DMN&FPNs	75.21	75.51	74.89	75.79	75.30
	All	76.07	76.27	75.87	76.55	75.93

sdSB-SVMs and sdSB-CNNs are constructed for each BFN, respectively; the sdMB-SVM and sdMB-CNN methods use all the six BFNs (DMN: default mode network; FPN1&2: two fronto-parietal networks; AN1&2: two attention networks; ECN: executive control network). In addition, the models with three BFNs (DMN, FPN1&2 (FPNs)) are also listed for comparison.

Compared to different sdSB-CNNs using only one BFN at a time, sdMB-CNN improved the diagnostic accuracy by 2.90–6.99% (p = 0.0001–0.08). For other performance metrics, sdMB-CNN also shows the best performance. The sdSB-CNNs with DMN, FPN1, and FPN2 have slightly improved performance (by 1.26–3.82%, p = 0.08–0.34), compared to those with other BFNs. The accuracy of sdMB-CNN using these three networks (i.e., DMN, FPN1&2) is close to that of the sdMB-CNN using all six networks with only a small increase (~1%), similar to the previous MB-CNN results.

Compared to the classification models using only sBFNs, the models using sdBFNs (with dynamic FC features added) show improved performance. Specifically, with all the six networks used, sdMB-CNN improved the diagnostic accuracy by 2.22% (p < 0.05) compared to the MB-CNN. Such improvement is similar to the improvement between MB-CNN and sdMB-CNN with three networks included (i.e., DMN, FPN1&2).

C. Extracted Static and Dynamic BFNs

Supplementary Fig. 1 shows paired static and dynamic BFNs for the six selected high-level cognitive functions, i.e., DMN, FPN1&2, AN1&2, and ECN, respectively, extracted from a randomly selected subject. In comparison between static and dynamic BFNs, we can generally figure out that the stronger the static FC is, the weaker FC dynamics are. Supplementary Videos 1–6 show time-varying BFNs of this subject, respectively.

IV. Discussion

A. General Discussion

We have proposed a novel framework to model the complex diagnostic spatial patterns of sBFNs and dBFNs derived from rs-fMRI for individualized eMCI detection. We first extract sBFNs by using GIG-ICA and the corresponding dBFNs by using time-varying seed-based correlation as a set of 3D image pairs. For each pair of sBFNs and dBFNs, we construct a 3D CNN to learn deeply embedded spatial patterns of both static and dynamic brain networks. Furthermore, we combined all the CNNs designed for different BFNs together to fuse the deep features of multiple functional systems in a unified framework for a joint eMCI classification.

For BFNs studies of MCI/AD, the majority of the previous papers used mass univariate methods to find out disease-related FC changes. This is usually insufficient to make individualized discrimination due to the small effect size overwhelmed by the large individual variability plus imaging noise. Motivated by the powerful feature representation ability of the CNN model in detecting discriminative spatial patterns from natural images, we design a CNN model for detecting eMCI-related patterns based on multiple BFNs from rs-fMRI. To make it more feasible for 3D CNN to be applied to the 4D (spatial + temporal) rs-fMRI data, we apply GIG-ICA to the 4D data to extract multiple BFNs in forms of 3D maps. We further extend the 3D CNN to a fused multiple-CNN model that integrates deep features from multiple BFNs in a unified framework. In addition to sBFNs, dBFNs are also adopted to further improve the diagnostic performance. We found that, using both sBFNs and dBFNs, we can improve diagnostic performance of eMCI. Once again, deep learning is superior to the traditional machine learning with the voxel-wise FC features.

B. Relation to Existing Works

To our best knowledge, this is the first deep learning framework based on paired static and dynamic BFNs for disease diagnosis. Previously, Zhao et al., proposed a 3D CNN model for automatic BFN component labeling for ICA-derived BFN from a group of healthy subjects [19]; however, that study just used static BFNs and focused only on a much easier task (i.e., component recognition), while our task (eMCI diagnosis) is substantially different and more difficult. Patterns of each BFN can be visually discriminable from other BFNs and other noise-related components. Without extensive training, one can easily accomplish this task. Zhao et al.’s method can be very effective in a task of identifying a particular component, but it does not touch BFN-based disease diagnosis, where the difference between a disease group and the healthy controls is more subtle (smaller effect size) and the diagnostic pattern could be more complex (deeply embedded features). Given its challenge, this study is very novel, among very few studies on eMCI detection.

Compared to our previous work on MICCAI 2018 [34], our current work also considered the temporal information of the BFNs. Instead of the direct usage of ICA-derived time series of each BFN, which can be regarded as the temporal characteristics of each BFN, we focused on more complex (thus more vulnerable to pathological attacks) patterns of dynamic FC. The dynamic FC was measured by voxel-wise seed-based correlation to the seed in the static BFN peak. A similar temporal variability measurement (i.e., standard deviation of dynamic FC) was used, similar to the metric used in our previous paper [6]. There are many other deep learning methods developed for analyzing time series data, such as recurrent neural network [31], gated recurrent unit [32], long short-memory net-work [33], and even 1D CNN [54], all of which can be also used to capture the temporal characteristics of dynamic FC. However, using our method, the dynamics of a BFN can also be represented by a 3D image, thus convenient for 3D CNN to learn from.

There are also several papers proposing “deep graph learning” based on generalized convolution neural networks to learn features from brain functional networks. For example, a common type of convolutional neural network on graphs was proposed to filter (convolute) the brain network embedded in high-dimensional, complex, irregular domain and encode the geometric structures in the network [55]. A connectome-convolutional neural network (CCNN) model was proposed to exert the convolution process on each region’s FC fingerprint to all other regions to encode the regions’ FC strength under an assumption that the disease could alter certain regions’ FC patterns [24]; see a more generalized, hierarchically designed CNN (namely, BrainNetCNN) in [25]. Another method proposed a graph kernel with a specific sorted pooling to sequentially encode a graph in a meaningful and consistent manner [56]. All these studies treated the BFNs as a graph with a number of nodes and edges. However, our method extracts features with more fine-grained, voxel-wise FC information considered. Recently, we also proposed a method considering temporal and spatial properties of region-wise dynamic connectivity networks [8], further verifying our assumption that both temporal and spatial information of the BFNs should be used for eMCI diagnosis. In a more generalized framework with CNN, we proposed an end-to-end deep learning framework that gradually extracts dynamic FC networks, region-level and network-level features [9]. Again, the fine-grained voxel-level features were not considered.

C. Brain Functional Networks With High Diagnostic Values

According to results in Section III.B, we showed the effectiveness of the proposed sdMB-CNN framework in extracting diagnostic features in terms of spatial FC and temporal variability of FC. The superiority of our method was demonstrated from two aspects: 1) Using sBFNs and dBFNs together is better than using sBFNs only; and 2) integrating features from different BFNs is better than that with any single BFN. The first one has been proved by many other dynamic FCbased diagnosis studies [6]–[11], and it is interesting to further investigate which BFN is more helpful in diagnosis of eMCI with the current deep learning framework. We found that the DMN and two FPNs have better performance compared to those of ECN and ANs, and such a result is consistent regardless which classifiers were used and whether dynamic BFNs were used or not (Tables 1 and 2). Therefore, we think that the DMN and FPNs could be more affected in the early stage of MCI. This is consistent with a seminal paper that proposed three large-scale brain networks (DMN, salient network, and central executive network (CEN)) as a unifying triple network model [57], where the CEN consists of both left- and right-sided FPNs. Both DMN and FPNs are regarded as the more neurocognitive networks because they have been observed activated or deactivated in a large set of high-level cognitive tasks and thus believed to mediate high-level cognitive functions [57], [58]. Importantly, their complex interactions and communications are believed to be fundamental to the healthy brain and mental status [56]. It is very likely that the triple networks have already been disturbed in the preclinical stage of AD [59]. Among them, the DMN turns to be the most important BFN in resting state and one of the most vulnerable networks to various neurological and psychiatric diseases [60], especially for AD [61]. Our study not only confirms previous findings, but also suggests that the complex spatiotemporal pattern changes in these high-level functional networks could be used for a better diagnosis of AD in even earlier stage.

D. Investigation of Potential Contributing Brain Areas

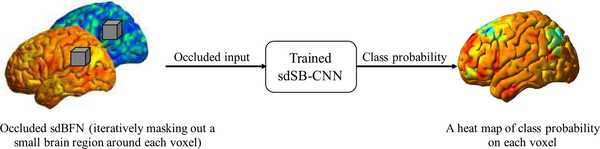
It is important to conduct further investigation on the potential important regions in the BFNs that contributed to the successful eMCI classification. We achieve this by generating heat maps color-coding the important brain regions in the BFNs using a method proposed in [62]. To do this, we fed the occluded input images of sBFNs and dBFNs (where a small region around each voxel was iteratively masked out) to the trained model and then recorded the class-assignment probability from the softmax function in the model for this voxel (Fig. 4). If the region is important to the classification model, by occluding it the classification accuracy will significantly drop. Therefore, the voxels in the heat map with lower probability values could have a greater impact on the classification as the performance would decrease if removing information from the occluded regions. We generated the heat maps for each trained sdSB-CNN that used each sdBFN as input, respectively.

Fig. 4.

An illustration for generating a heat map of class probability to further reveal which regions in the paired brain functional networks contributed to the eMCI classification.

Fig. 5 shows the mean heat maps for the three networks with a superior classification performance than others, i.e., DMN, FPN1&2. Since it takes a lot of time to generate a heat map, we used 10 randomly selected subjects for the mean heat maps. Note that, the voxels with lower probability (blue) correspond to a greater impact on the eMCI classification. The heat map of the DMN indicates that the medial prefrontal cortex and precuneus have a greater impact for eMCI classification. The results are consistent with previous studies, where FC and cortical thickness are found to be altered in the precuneus [63]–[69] and the medial prefrontal cortex [66]–[70] in AD and MCI patients. However, the other parts of the DMN seem less important to the classification model. It seems that, during early MCI stage, the midline portion of the DMN is more likely to be involved.

Fig. 5.

Mean heat maps from 10 randomly selected subjects for three major networks (A) DMN, (B) FPN1, and (C) FPN2, respectively. The voxels with lower probability (blue) have a greater impact on classification.

In the two FPNs, left angular gyri, right posterior parietal cortex, and right dorsolateral prefrontal cortex are shown in Fig. 5, indicating that these regions are more likely to be affected in eMCI subjects. These regions are the association cortices in the fronto-parietal areas, where multiple inputs are integrated and processed. Their functions include attention maintaining, control manipulating, working memory, decision making, among many of others [71]–[73]. While it is well known that AD and MCI patients showed changed functions and structures in the angular gyrus [63], [74], [75] and the fronto-parietal regions [63], [76], [77], it is the first time that these regions are suggested to be informative to a deep learning-based diagnostic model in the early stage of MCI.

Note that our model does not only indicate the importance of the aforementioned regions, but also the importance of their complex patterns, in early AD diagnosis. These patterns may include the spatial FC pattern, the temporal FC variability pattern, and/or their interactions, or even the high-level interactions at these regions among the high-level cognitive function-related networks [57]. It is the drawback of deep learning that we cannot provide clinically valuable information about which specific pattern(s) is changed. However, as we have identified these regions as potential biomarkers, more validation studies can be carried out focusing on these regions.

E. Effects of Length of Sliding Window for dBFNs

We performed an additional experiment with different lengths of sliding window (20, 30, and 40 time points) for the dynamic default mode network (DMN) to clarify how this parameter affects the classification performance. The results are summarized in Table 1 of Supplementary Materials. In the experiment, the sdSB-CNN using 30 time points shows slightly improved accuracy by 0.23% (p = 0.82, Friedman test) and 0.8% (p = 0.83) over those using 20 time points and 40 time points, respectively; but there are no significant differences. Thus, we adopted 30 time points as the parameter in the main result, although such a parameter did not significantly change the result.

F. Limitations and Future Works

In this study, we preselected a small number of BFNs which are known to be highly related to eMCI. However, there is a possibility that other BFNs may also be changed in eMCI and thus contain diagnostic information. However, our model can be conveniently extended to include all BFNs. The only concern is that an adequate sample size is needed if more BFNs are involved. Second, the ICA model we used requires a priori BFN templates. One of our ongoing work is to take the variability of ICA and template selection into consideration in a more complex model. Finally, we only used seed-based FC’s variation as the measurement of dynamic FC. There are many other dynamic FC metrics characterizing more complex functional interactions can be used, such as the temporal complexity measured by fractal dimension of dynamic FC. Combining such information into deep learning models could further improve the performance of brain disease diagnosis.

V. Conclusion

In this paper, we proposed a novel deep learning framework based on multiple paired static and dynamic brain functional networks (BFNs) to learn deeply-embedded spatial patterns of the static and dynamic BFNs for eMCI diagnosis. Experimental results on a large publicly accessible dataset demonstrated the superiority of the proposed method compared to traditional voxel-based analysis. The proposed framework provides a convenient and straightforward tool for accurate individualized diagnosis of various neurological and psychiatric diseases.