Fig. 2.

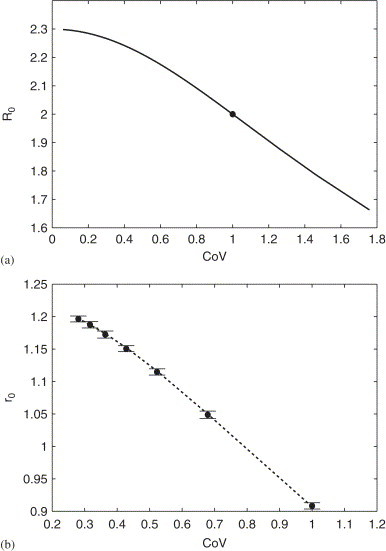
(a) $R_0$ for the epidemiological spread of HIV is plotted with respect to the CoV of the transition time to AIDS. The dot denotes the case when these transition times are exponentially distributed; the distribution is described by a Weibull distribution with shape parameter $\rho$ and mean $1/v$ (see text for details). All other lifetime distributions are assumed to be exponential. $v=0.083{\mathrm{year}}^{-1}$ (Blower et al., 2001), $\mu =0.032{\mathrm{year}}^{-1}$ (Blower et al., 2001) and $r\beta =0.23{\mathrm{year}}^{-1}{\mathrm{individual}}^{-1}$ such that $R_0$ for the ODE model is 2 (Blower and McLean, 1994, Valesco-Hernandez et al., 2002). (b) The initial growth rate $r_0$ for the in-host HIV model is plotted as a function of the CoV of the Weibull distribution of cell death times (dotted line); both uninfected and infected cells were assumed to have the same shape parameter although different means. Here $r_0$ is the solution to Eq. (23) when $b(t)=\mathit{kQ}$ and $f(t)={\int }_{r=0}^t{e}^{-(u+\beta x_0)r}\beta e^{-(\sigma (t-r){)}^{\rho }}\mathit{dr}$, when $\sigma =a\mathrm{\Gamma }(1+1/\rho )$. The dots and error bars give $r_0\pm$ one standard error of the mean as computed by Monte Carlo simulation (see Heffernan and Wahl, 2005). Parameters values: $\lambda =100$ cells $\mu {\mathrm{l}}^{-1}{\mathrm{day}}^{-1}$, $d=0.1{\mathrm{day}}^{-1}$, $\beta =0.0032{\mathrm{day}}^{-1}$, $a=0.5{\mathrm{day}}^{-1}$, $Q=0.05$, $k=62.5{\mathrm{day}}^{-1}$ and $u=3{\mathrm{day}}^{-1}$ (Perelson and Nelson, 1999, Wahl and Nowak, 2000, Smith and Wahl, 2004).