Figure 1.
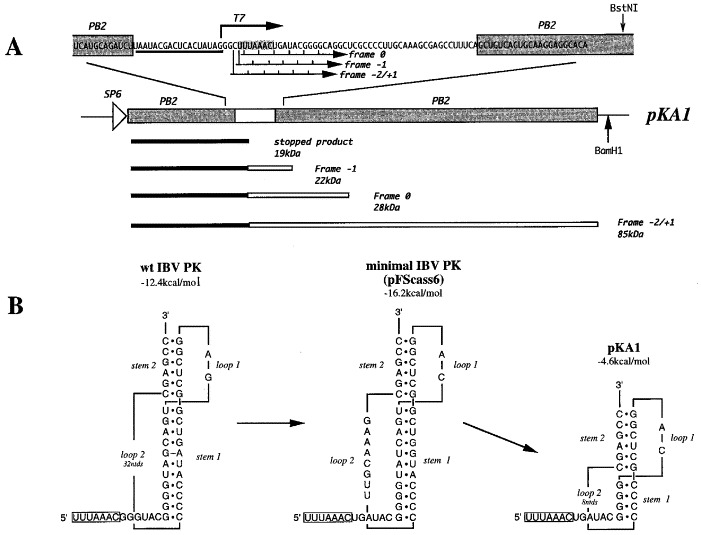
The frameshift reporter construct pKA1. (a) Plasmid pKA1 was derived from pFScass 6 (Brierley et al., 1992) by site-directed mutagenesis (see Materials and Methods). pKA1 contains a truncated version of the minimal IBV pseudoknot (white box) cloned into a reporter gene, the influenza PB2 gene (shaded boxes). Linearisation of the plasmid with BamH1 and in vitro transcription using SP6 RNA polymerase yields an mRNA (2.4kb) that, when translated in RRL, is predicted to produce a 19 kDa non-frameshift product corresponding to ribosomes that terminate at the UGA termination codon (located immediately downstream of the slippery sequence UUUAAAC, shaded), and a 22 kDa −1 frameshift product. The 0-frame and −2/+1 frames are also open (to some extent) in this construct. Ribosomes which enter these frames produce 28 kDa and 85 kDa products respectively. A bacteriophage T7 promoter is present just upstream of the frameshift region; this promoter is employed to generate short, pseudoknot-containing transcripts from BstNI-digested templates for secondary structure analysis. (b) The wild-type (wt) IBV, the minimal IBV and the pKA1 pseudoknots (PK). The minimal IBV frameshift signal present in pFScass 6 is based on the wild-type IBV frameshift signal and is fully functional in frameshifting (Brierley et al., 1992). It differs from the wild-type in a number of ways; a termination codon (UGA) is present immediately downstream of the slippery sequence (UUUAAAC, boxed) to terminate zero frame ribosomes, loop 2 of the pseudoknot contains 8 rather than 32 nt, the G·A mismatched pair in stem 1 of the wild-type pseudoknot is replaced by a U·G pair, the G nucleotide of loop 1 is replaced by a C nucleotide and, finally, the minimal pseudoknot has no stop codons. Plasmid pKA1 was derived from pFScass 6 by deletion mutagenesis (see Materials and Methods). The type and number of bases in the loops and stem 2 remained unaltered. The predicted stability of stem 1 of each construct is shown (calculated according to the rules by Turner et al., 1988, using a loop length of 8 nt; see the text).
