Paradox of enrichment: A fractional differential approach with memory

Abstract

The paradox of enrichment (PoE) proposed by Rosenzweig [M. Rosenzweig, The paradox of enrichment, Science 171 (1971) 385–387] is still a fundamental problem in ecology. Most of the solutions have been proposed at an individual species level of organization and solutions at community level are lacking. Knowledge of how learning and memory modify behavioral responses to species is a key factor in making a crucial link between species and community levels. PoE resolution via these two organizational levels can be interpreted as a microscopic- and macroscopic-level solution. Fractional derivatives provide an excellent tool for describing this memory and the hereditary properties of various materials and processes. The derivatives can be physically interpreted via two time scales that are considered simultaneously: the ideal, equably flowing homogeneous local time, and the cosmic (inhomogeneous) non-local time. Several mechanisms and theories have been proposed to resolve the PoE problem, but a universally accepted theory is still lacking because most studies have focused on local effects and ignored non-local effects, which capture memory. Here we formulate the fractional counterpart of the Rosenzweig model and analyze the stability behavior of a system. We conclude that there is a threshold for the memory effect parameter beyond which the Rosenzweig model is stable and may be used as a potential agent to resolve PoE from a new perspective via fractional differential equations.

Highlights

• •We formulate the fractional counterpart of the Rosenzweig model.
• •We analyze the stability of this fractional order model.
• •We identify a threshold for the memory effect parameter.
• •Below this threshold value the system is always stable independent of enrichment.
• •Fractional differential equations may be an important tool for resolving the paradox of enrichment.

1. Introduction

The paradox of enrichment (PoE) phenomenon in population ecology was first proposed by Michael Rosenzweig in 1971  [1]. Rosenzweig observed that enrichment may destroy the steady state of a predator–prey system. He formulated his model using ordinary differential equations (ODEs) and considered enrichment by increasing the prey-carrying capacity. He observed that this gradually leads to destabilization of the system, usually into a limit cycle. This cyclical pattern was further studied by May  [2] and Gilpin and Rosenzweig  [3]. Enrichment leads to destabilization of the equilibrium of the Rosenzweig and many other models  [4]; huge amplitudes occur that frequently drive population densities to very low values and this may result in extinction. The word “paradox” is used because enrichment leads to extinction. Since the 1990s, the word “paradox” has also been associated with the fact that destabilization is not always (or rarely) observed in natural environments, as discussed by Jensen and Ginzburg  [5]. They reviewed the literature on experimental attempts to demonstrate PoE and found an insufficient number of studies in favor of PoE. Some commonly misinterpreted examples and experiments (artificial lake eutrophication, Didinium–Paramecium systems  [6], [7], Rotifer–Algae systems  [8]) addressing the question of whether PoE exists need further discussion.

Several theoretical and empirical studies have been carried out in attempts to explain the PoE phenomenon. Roy and Chattopadhyay provide a detailed review of the studies and a brief overview of the proposed solutions  [4]. They described some reasonable mechanisms, such as the presence of inedible prey, invulnerable prey, unpalatable prey, ratio-dependent functional responses, spatiotemporal chaos, inducible defense, density-dependent predator mortality and toxic food, to resolve the paradoxical outcome of ecosystem enrichment. Several additional mechanisms have also been proposed. For example, Abrams and Roth proposed refuges and immigration as a possible solution  [9]. More recently, Mougi and Nishimura showed that rapid trait evolution of predator–prey species can stabilize the system  [10]. An imperfect optimal foraging mechanism was proposed by Mougi and Nishimura  [11]. Rall et al. predicted that a sigmoidal or predator inference functional response can dampen population oscillations due to enrichment that resolves PoE  [12]. Disease in ecological systems has been recognized as an essential mechanism in different ecological issues. Sharp and Pastor recently considered a density-dependent susceptible deer population, an infected population and an environmental pool of prions that infect the deer population  [13]. They showed that the disease population has the ability to dampen population oscillations. Solutions to the PoE problem have been established by several authors from diverse perspectives and dimensions, but most of the solutions have some common factors associated with the behavioral aspects of predator–prey species at the individual level and inducible or morphological defense mechanisms of the prey. However, solutions that consider community-level organization are still lacking. Knowledge of how learning and memory modify behavioral responses to species is a key factor in making a crucial link between the species and community levels  [14]. Resolution of PoE via these two organizational levels can be interpreted as a microscopic- and macroscopic-level solution.

In statistical physics the connection between microscopic dynamics in a stochastic system and a macroscopic description of their behavior as a whole is very attractive  [15]. It has been already established that the macroscopic behavior of stochastic systems contains a manifestation of microscopic dynamics due to memory effects  [15].

Memory in the biological domain in physical systems is manifest as a series of events that induce episodic memory [16], [17] containing information about past and present events and can help in making future decisions  [18]. Biological systems are also enriched with ecological memory  [19]. Memory relates to historic events and requires an entire long-term record for analysis. For example, seasonal succession of phytoplankton in lakes responds to small changes in trophic structure and natural fluctuations of gradients  [19]. Aquatic and phytoplankton systems possess a remarkable memory of climatic events [20]. Apart from such climatic phenomena, aquatic zooplankton exhibit memory-based phenomenological responses: small changes in the environment induce morphological defense organs such as helmet formation and the development of spines through cyclomorphosis  [21]. These changes are due to a mixed seasonal and genetically inherited reaction  [22] induced over long time scales, suggesting a phenotypic change through memory-based actions. Prey refuge, group hunting and prey swarming are all well-coordinated actions based on memories of past events that lead to cultural learning  [14]. Experience accrued through learning may direct anti-predator responses  [23], [24], [25]. In aquatic systems, learning of chemical cues and the production of counter responses are well documented among zooplankton  [26], [27], [28], [29], [30], [31]. Westerlund remarked that, surprisingly, even “dead matter has memory”  [32]. A recent study by Zheng et al.  [33] revealed that discrete earthquake events are related to seismic memory.

Fractional derivatives provide an excellent tool for describing memory and the hereditary properties of various materials and processes  [34], [35]. In other words, fractional dynamic systems in applications can adequately represent some long-term memory and non-local effects that are typical for many anomalous processes  [36]. In this calculus, a Caputo derivative implies a memory effect via convolution between an integer-order derivative and a power of time  [37]. Note that a fractional-order system is more stable than its integer counterpart since the stability domain in the complex space of eigenvalues of the linearized system for fractional differential equations (FDEs) remains contained and is larger than the corresponding domain for ordinary differential equations  [38]. FDEs also help in reducing errors arising from neglected parameters in modeling of real-life phenomena  [39].

Ahmed and Elgazzar used FDEs to study non-local epidemics synergistic with other complex adaptive systems such as severe acute respiratory syndrome, avian flu, and foot-and-mouth disease  [40]. Local and non-local interactions were widely observed in recent outbreaks of the above diseases and the model proposed by Ahmed and Elgazzar captured these interactions. Arafa et al. also used FDEs to elegantly model childhood diseases with constant vaccination and obtained an approximate analytic solution through the homotopy analysis method  [41]. Immune systems include both antigen-specific and systematic response and involve memory. A fractional-order example of two immune effectors attacking an antigen was proposed by Hashish and Ahmed  [42]. Apart from ecology and epidemiology, FDEs have interdisciplinary applications in various fields. For example, nonlinear earthquake oscillations can be modeled using fractional derivatives  [41] and a fluid-dynamics traffic model with fractional derivatives can eliminate the efficiency arising from assumption of continuous traffic flow  [41]. Gomez et al. used a fractional temporal operator in RC equivalent circuits to modify the standard Kirchhoff law in an FDE domain  [43].

Many researchers have tried to resolve PoE from different perspectives but to the best of our knowledge there have been no studies involving FDEs. Here we formulate a fractional counterpart of the Rosenzweig model and analyze the stability of the model. We infer that there is a critical threshold of the memory effect parameter beyond which the Rosenzweig system is stable and we thus resolve PoE from a new perspective.

The remainder of the paper is organized as follows. We describe local and non-local kernels in Section  2. In Section  3 we present our mathematical model with highlight the existence and uniqueness of its solution. In Section  4 we investigate the model behavior around ecologically feasible equilibria. The paper ends with results and conclusions.

2. Local and non-local kernels

It is well known that integer-order derivatives have local kernels with clear physical interpretations, which significantly simplifies their use for solving applied problems in various fields of science. However, this is not true in the case of fractional-order integrals and derivatives, which have non-local kernels. Nevertheless, there is rapidly growing interest in both theory and applications to real world problems  [44]. The physical interpretation of fractional integration and differentiation is based on cosmic time and individual time  [45].

The fractional integral of a function is generally interpreted as the real distance passed by a moving object, for which the recorded local values of its speed represent individual speed and the local values of time represent individual time. The relationship between the locally recorded time (which is considered as flowing equably and is represented as $t$) and cosmic time (which is considered as flowing non-equably) $\tau$ is given by a known mathematical function $g_t\left(\tau \right)$. The function $g_t\left(\tau \right)$ describes the inhomogeneous time scale, which depends on both $\tau$ and $t$, which here is the last value measured for the individual time of the moving object. When $t$ changes, the entire preceding cosmic time interval changes as well. The derivative of this distance based on local time, which is also a function of non-local time, is interpreted as the fractional derivate  [45]. In other words, the homogeneous time scale is just an ideal notion and is necessary for developing mathematical models describing inhomogeneous cosmic time and its change. Thus, the ideal model of equably flowing homogeneous time can be considered as a rough approximation of cosmic time, which is non-local  [45]. Fractional dynamical systems adequately represent some long-term memory and these non-local effects that are typical for many anomalous processes  [36]. Such non-local effects can be captured through the fractional differential operator, which has a power law form  [46].

Several mechanisms have been proposed to resolve the PoE problem. This universally accepted theory is still an unachieved goal because most researchers consider only local effects and ignore non-local effects, which capture memory.

3. Model formulation

There are many definitions of fractional derivatives. Those most frequently used are the Grunwald–Letnikov, Riemann–Liouville (RL), and Caputo definitions  [44], [47], [48], [49]. Note that the zero singularity inherent to the RL derivative may pose challenges and difficulties. The Caputo derivative needs more regularity as it uses the first derivative of the function in question, whereas the RL derivative does not require as much smoothness. In the Caputo case the derivative of a constant is zero and we can properly define the initial conditions for FDEs so that they can be handled analogously to the classical integer case. The Caputo derivative implies a memory effect by means of a convolution between the integer-order derivative and a power of time  [44], [48], [49].

We consider the model proposed by Rosenzweig  [1, Model 4] and explicitly studied by Gilpin  [3]. The model is as follows:

$$\frac{dN}{dt}=rN(1-\frac{N}{K})-kP(1-e^{-cN})$$$$\frac{dP}{dt}=AkP(e^{-cJ}-e^{-cN})\text{,}$$ (3.1)

where $N$ is prey density and $P$ is predator density. $K$ is the prey carrying capacity. The predator isocline is at $N=J$. The other parameters of (3.1) influence the shape of the prey zero isocline and the rate of system response  [3]. We assume that all parameters are positive.

Now we introduce fractional order into model (3.1). The fractional Rosenzweig model is obtained from the classical equations by replacing the first-order time derivatives by fractional derivatives of order $\alpha$, where $0<\alpha <1$. The fractional relaxation equations  [50], [51], [52] contain an integral operator with a slowly decaying power law kernel so that the process is not Markovian and depends on the prehistory of the system  [46], [53].

The new system is described by the following set of FDEs:

$$D^{\alpha }N\left(t\right)=rN(1-\frac{N}{K})-kP(1-e^{-cN})$$$$D^{\alpha }P\left(t\right)=AkP(e^{-cJ}-e^{-cN})\text{,}$$ (3.2)

where $D^{\alpha }y\left(x\right),\alpha \in (0,1]$ is the fractional-order derivative of $y$ in the sense of Caputo, defined as

$$D^{\alpha }y\left(x\right)≔I^{m-\alpha }{y}^m\left(x\right)\text{,}x>0\text{,}$$

where $m=\left[\alpha \right]$ is the value of $\alpha$ rounded up to the nearest integer, $y^m\left(x\right)$ is the usual $m$th derivative of $y\left(x\right)$,

$$I^{\beta }z\left(x\right)≔\frac{1}{\Gamma \left(\beta \right)}{\int }_0^x{(x-t)}^{\beta -1}z\left(t\right)dt$$

is the RL integral operator of order $\beta >0$, and $\Gamma \left(\beta \right)$ is the gamma function  [44], [47], [48], [49], [54].

We are now in a position to discuss the existence and uniqueness of the solution of (3.2). Consider the fractional-order Rosenzweig predator–prey system (3.2) with initial conditions $N\left(0\right)=c_1,P\left(0\right)=c_2$. This can be written as

$$D^{\alpha }N\left(t\right)=f_1(N,P)$$$$D^{\alpha }P\left(t\right)=f_2(N,P)$$ (3.3)

with initial conditions $N\left(0\right)=c_1,P\left(0\right)=c_2$.

Let $I=[0,T],T<\infty$, and let $C^2\left(I\right)$ be the class of all continuous column vector functions $X\left(t\right)=(N\left(t\right),P\left(t\right))$ defined on $I$ with norm

$${\Vert X\Vert }^{\ast }=\underset{t}{sup}{e}^{-Mt}\left|N\left(t\right)\right|+\underset{t}{sup}{e}^{-Mt}\left|P\left(t\right)\right|\text{,}M>0\text{,}$$ (3.4)

which is equivalent to the sup-norm $\Vert X\Vert ={sup}_t\left|N\left(t\right)\right|+{sup}_t\left|P\left(t\right)\right|$. When $t>\sigma \ge 0$, we write $C^2\left(I_{\sigma }\right)$.

Let $L_1^2\left(I\right)$ be the class of all Lebesgue-integrable column vector functions on $I$ with norm

$${\Vert X\Vert }_1={\int }_0^T\left|e^{-Mt}N\left(t\right)\right|dt+{\int }_0^T\left|e^{-Mt}P\left(t\right)\right|dt\text{,}$$

which is equivalent to the norm ${\Vert X\Vert }_{L_1}={\int }_0^T\left|N\left(t\right)\right|dt+{\int }_0^T\left|P\left(t\right)\right|dt$.

Now we consider the following assumptions  [55].

• 1. $f_i:D\to {\mathbb{R}}^{+},D\subset {\mathbb{R}}_2^{+}$.
• 2. $\frac{\partial f_i(N,P)}{\partial N},\frac{\partial f_i(N,P)}{\partial P}$ ($i=1,2$), exists and is bounded on $D$.

Condition (2) implies that the functions $f_i$ satisfy the Lipschitz condition

$$|f_i(N,P)-f_i(N_1,P_1)|\le M_1{\Vert X\left(t\right)-X_1\left(t\right)\Vert }_2\text{,}$$ (3.5)

where ${\Vert X\left(t\right)-X_1\left(t\right)\Vert }_2=|N\left(t\right)-N_1\left(t\right)|+|P\left(t\right)-P_1\left(t\right)|$ and $M_1\ge \left|\frac{\partial f_i}{\partial N}\right|,\left|\frac{\partial f_i}{\partial P}\right|$ for $i=1,2$.

Lemma 1

System   (3.3)   with initial conditions can be written in the form

$$D^{\alpha }X\left(t\right)=F\left(X\left(t\right)\right)\text{,}t\in (0,T]\text{and}X\left(0\right)=X_0\text{,}$$ (3.6)

where $X\left(t\right)=\left(\begin{array}{c}\hfill N\left(t\right)\hfill \\ \hfill P\left(t\right)\hfill \end{array}\right),F\left(X\left(t\right)\right)=\left(\begin{array}{c}\hfill f_1(N,P)\hfill \\ \hfill f_2(N,P)\hfill \end{array}\right)$ and $X_0=\left(\begin{array}{c}\hfill N\left(0\right)\hfill \\ \hfill P\left(0\right)\hfill \end{array}\right)$ .

Now let $D=\{X\in {\mathbb{R}}^2:0\le X\le B\}$. Then (3.3) satisfies conditions (1) and (2) with $M_1=max\{B,rB,AkcB,Ak\}$.

Now we have the following theorem.

Theorem 1

Let assumptions  (1)  and  (2)  be satisfied. Then the initial value problem   (3.3)   has a unique solution $X\in C^2\left(I\right)$ , $X^{\prime }\in C^2\left(I_{\sigma }\right)$ , and $X^{\prime }\in L_1^2\left(I\right)$ .

Proof

The proof follows from  [55, Theorem 1]. □

An approximate analytic solution of system (3.2) obtained using the homotopy analysis method  [56] is presented in Appendix A.

4. Equilibrium points and stability analysis

The equilibrium points of system (3.2) are $E_0(0,0)$, $E_1(K,0)$ and $E(J,\frac{rJ(1-\frac{J}{K})}{k(1-e^{-cJ})})$.

The Jacobian matrix at $E_0(0,0)$ is

$$J_0=\left(\begin{array}{cc}\hfill r\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill Ak(e^{-cJ}-1)\hfill \end{array}\right)\text{.}$$

The eigenvalues corresponding to $E_0$ are $r,Ak(e^{-cJ}-1)$, so $E_0$ is unstable for all $\alpha \in (0,1]$.

The Jacobian matrix at $E_1(K,0)$ is

$$J_1=\left(\begin{array}{cc}\hfill -r\hfill & \hfill -k(1-e^{-cK})\hfill \\ \hfill 0\hfill & \hfill Ak(e^{-cJ}-e^{-cK})\hfill \end{array}\right)\text{.}$$

The eigenvalues corresponding to $E_1$ are $-r,Ak(e^{-cJ}-e^{-cK})$, so $E_1$ is locally asymptotically stable if $K<J$.

The Jacobian matrix at $E(J,\frac{rJ(1-\frac{J}{K})}{k(1-e^{-cJ})})$ is

$$J=\left(\begin{array}{cc}\hfill r-\frac{2rJ}{K}-\frac{crJ(1-\frac{J}{K})e^{-cJ}}{(1-e^{-cJ})}\hfill & \hfill -k(1-e^{-cJ})\hfill \\ \hfill \frac{ArJc(1-\frac{J}{K})e^{-cJ}}{(1-e^{-cJ})}\hfill & \hfill 0\hfill \end{array}\right)\text{.}$$

The eigenvalues corresponding to $E$ are

$${\lambda }_1=\frac{1}{2}[r-\frac{2rJ}{K}-\frac{crJ(1-\frac{J}{K})}{(1-e^{-cJ})}{e}^{-cJ}+\sqrt{{(r-\frac{2rJ}{K}-\frac{crJ(1-\frac{J}{K})}{(1-e^{-cJ})}{e}^{-cJ})}^2-4AkcrJ(1-\frac{J}{K})e^{-cJ}}]$$

$${\lambda }_2=\frac{1}{2}[r-\frac{2rJ}{K}-\frac{crJ(1-\frac{J}{K})}{(1-e^{-cJ})}{e}^{-cJ}-\sqrt{{(r-\frac{2rJ}{K}-\frac{crJ(1-\frac{J}{K})}{(1-e^{-cJ})}{e}^{-cJ})}^2-4AkcrJ(1-\frac{J}{K})e^{-cJ}}]\text{.}$$

A sufficient condition for the local asymptotic stability of the equilibrium point $E$ is

$$\left|arg\left({\lambda }_i\right)\right|>\frac{\alpha \pi }{2}\text{,}i=1,2\text{.}$$ (4.1)

5. Results and conclusion

The major review of empirical and theoretical PoE studies presented by Roy and Chattopadhyay  [4] provides a number of plausible solutions and partial resolution of the problem. The experimental evidence was challenged by Jensen and Ginzburg  [5], who showed that most examples proposed as evidence of PoE are insufficient to justify the phenomenon in natural systems. A common example of PoE is the process of lake eutrophication. Enrichment of aquatic systems appears to increase the carrying capacity of producers and leads to a bloom that covers the lake. PoE may be suggested as a cause of this phenomenon, but in fact it is the limiting dissolved oxygen that is responsible for system collapse in this case, irrespective of the enrichment response. Other empirical studies using the Didinium–Paramecium system were carried out by Luckinbill  [6] and Veilleux  [7]. Both authors showed that the system proposed by Gause  [57] could be modified to allow coexistence of predator and prey. Addition of methyl cellulose prevented the extinction of any of the species in the system and provided an artificial refuge for prey species. Similarly, a study of Rotifer–Algae by Fussmann et al. showed that predator extinction resulted from enrichment  [8]. Similar to the experiments of Luckinbill and Veilleux, the results showed that reducing nutrient input can bring the system from a region of consistent predator extinction to a region of coexistence. Capture of this ubiquitous dynamic behavior involved in PoE remains an open problem from both theoretical and ecological perspectives.

Here we considered the Rosenzweig model of PoE to provide a plausible solution from a new perspective that considers the ecological memory that exists for most species. Most of the solutions proposed so far involve species-level organization and ignore the community level. As a consequence, the impact of memory on system dynamics has been neglected. This memory can be well captured by a fractional derivative consisting of non-local operators.

The memory effect can also be incorporated using other frameworks such as Volterra integral equations and delay differential equations  [58]. Volterra integral equations describe systems with continuously distributed memory over all past events. For example, the spread of epidemics with a general (not necessarily exponential) distribution of infection times can be modeled by Volterra integral equations. In another example, the evolution of a set of competing biological species with memory can be modeled through a system of integro-differential equations, which can be reduced to a system of Volterra integral equations  [58]. Besides population dynamics, the evolution of capital stock under an investment strategy can be described by a Volterra integral equation.

In an ODE system in ecology, the representation of a process by a function is often based on experiments. The response of the function chosen can be fitted to experimental data. This functional response should not be derived mechanistically but phenomenologically  [59]. The functional response may be prey- and/or predator-dependent according to experimental results. Naturally, these types of experiment can have various time lengths and integrate memory. Note that even if an ODE describes an instantaneous process, the notion of instant depends on the time scale considered, whereas FDEs have the property of fading memory and depend on the range of $\alpha$ ($0<\alpha <1$). Such memories can describe current events with the collective information from preceding events, while events in the far past can often be neglected compared to contributions from the near past  [60]. Volterra defined the notion of fading memory as “the principle of dissipation of hereditary action”  [61]. Podlubny  [44] called this the “short memory principle”.

In this study we used FDEs to capture the memory effect in an ecological framework. Naturally we expect that our modified Rosenzweig model (3.2) with memory characterized by $\alpha \in (0,1)$ is more stable than the classical Rosenzweig model with integer $\alpha (=1)$. Note that $\alpha$ plays a key role in understanding memory effects on species. The system sensitivity with respect to $\alpha$ is an important aspect to be discussed. We analyzed the sensitivity of model (3.2) with input parameter $\alpha$ and output the range of $K$ up to which the system is stable (Appendix C). We observe that when the value of $\alpha$ decreases, the system has a high elasticity index, that is, the system is more sensitive with respect to $\alpha$.

Since most FDEs do not have exact analytic solutions, approximation and numerical techniques must be used. Several analytical and numerical methods exist for solving FDEs. For numerical solution of (3.2), we used the FDE12 package in Matlab which is an implementation of the Adams–Bashforth–Moulton predictor–corrector method  [62], [63], [64], [65]. The parameter values listed in Table 1 were used.

Table 1.

Parameter values used to solve (3.2) (taken from [3]).

Parameter	$r$	$k$	$c$	$A$	$J$
Value	0.05	0.025	0.1	1	20

Fig. 1 (a) shows that the classical Rosenzweig model with no memory is stable for a carrying capacity of $K=48$. When we enrich the prey carrying capacity $(K=60,K=80)$ and keep the other parameter fixed, the system destabilizes (Fig. 1(b) and (c)). However, when we incorporate the memory effect in the classical model with $\alpha \in (0,1)$, the system no longer shows a pattern of destabilization on enrichment (Fig. 2, Fig. 3 ). Fig. 4 shows that the system has a memory threshold $(\alpha \approx 0.2332)$ below which it is always stable, even if we further increase the carrying capacity without restriction. Mathematically this intermediate value of $\alpha$ can be interpreted as a filter with partial memory that falls between two extreme filters with complete memory and with no memory  [66].

Fig. 1.

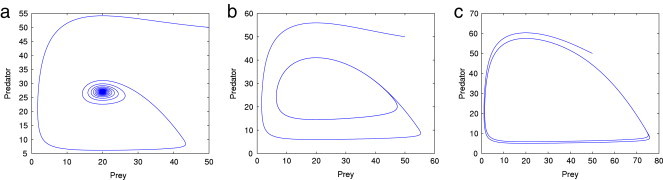
Phase-plane diagram depicting the trajectory of predator–prey density for interior equilibrium of the classical Rosenzweig model with no memory $(\alpha =1)$ and gradual enrichment of the system through the carrying capacity $K$. (a) exhibits a stable trajectory with low enrichment ($K=48$) whereas (b) shows a limit-cycle oscillation under moderate enrichment ($K=60$) and (c) exhibits a limit-cycle oscillation with greater amplitude for high enrichment ($K=80$).

Fig. 2.

Phase-plane diagram depicting the trajectory of predator–prey density for interior equilibrium of the classical Rosenzweig model with memory effect parameter $\alpha =0.86$, with gradual enrichment of the system through the carrying capacity $K$. (a) and (b) exhibit a stable trajectory for moderate ($K=48$) and high ($K=60$) carrying capacities but (c) shows limit-cycle oscillation for high enrichment ($K=80$).

Fig. 3.

Phase-plane diagram depicting the trajectory of predator–prey density for interior equilibrium of the classical Rosenzweig model incorporating the memory effect parameter $\alpha =0.68$, with gradual enrichment of the system through different levels of the carrying capacity $K$. All the subplots exhibit a stable trajectory.

Fig. 4.

The parameter regions in which the interior equilibrium is stable (blue region) or unstable based on $\alpha$ and $K$. (a) A system with no memory $(\alpha =1)$ allows stable equilibrium for a carrying capacity of $K\approx 50$. (b) System with a memory threshold $(\alpha \approx 0.2332)$ below which it is always stable for all further increases in the carrying capacity. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

The individual-level organization discussed above is mainly associated with the behavioral aspects of predator–prey relationships and inducible or morphological prey mechanisms. Learning and memory can modify these anti-predator behavioral responses, which is key to making the link between individual-level processes and higher-level organization in ecological systems  [14]. For example, prey refuge is one of the most manifest and well-coordinated actions based on memories of past events that lead to cultural learning  [14]. To illustrate this issue, we incorporated a refuge parameter in the fractional-order Rosenzweig model. The individual-level solution of PoE with a refuge effect can be obtained from model (3.2) with $\alpha =1$. The community-level solution based on memory can be illustrated by model (3.2) with $\alpha \in (0,1)$. Conditions for which the modified Rosenzweig model is stable are given in Appendix B. The region of stability for the corresponding enrichment parameter $\left(K\right)$ and refuge parameter $\left(m\right)$ expands if we gradually increase the memory effect in comparison to a system with no memory (Fig. 5 ). Estimation of the model parameters for such a system is an important task from a data analysis perspective. The total least squares approach is suitable for this purpose and we applied this method to illustrate model (3.2) and fitted an estimated curve for a simulated data set (Appendix C). This memory phenomenon is clearly an approximate tradeoff between fractional differentiation and stability. Against this backdrop, we conclude that ecological memories can protect a system against destabilization and may represent a potential agent for resolving PoE from a new perspective using FDEs.

Fig. 5.

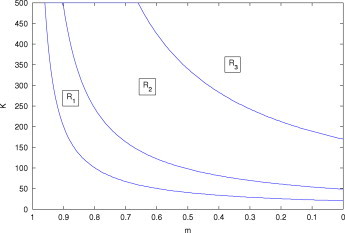
Domain of the stability region in which the interior equilibrium of the Rosenzweig model with a refuge effect (B.1) is stable or unstable based on the carrying capacity $\left(K\right)$ and refuge parameter $\left(m\right)$. (a) Region $R_1$ corresponds to the system with no memory $(\alpha =1)$. (b) The expanded region comprising $R_1$ and $R_2$ together corresponds to the system with memory effect parameter $\alpha =0.5$. (c) The largest region comprising $R_1$, $R_2$ and $R_3$ represents the system with memory effect parameter $\alpha =0.2$.

Appendix A.

An approximate analytic solution: homotopy analysis method

In this appendix we apply the homotopy analysis method  [56] to obtain a numerical analytical solution for fractional system (3.2).

We choose the base function as $\left\{t^{(n+m)\alpha }\right|n,m\ge 0\}$, so the solutions are of the form

$$N\left(t\right)=a_{0,0}+\sum _{n,m=0}^{\infty }{a}_{n,m}{t}^{(n+m)\alpha }$$$$P\left(t\right)=b_{0,0}+\sum _{n,m=0}^{\infty }{b}_{n,m}{t}^{(n+m)\alpha }\text{,}$$ (A.1)

where $a_{n,m},b_{n,m}$ are the coefficients. It is straightforward to choose $N_0\left(t\right)=c_1,P_0\left(t\right)=c_2$ as our initial approximation of $N\left(t\right)$ and $P\left(t\right)$, and the linear operator is then

$$L_{\alpha }\left[\hat{N}\right]=D^{\alpha }\hat{N}$$$$L_{\alpha }\left[\hat{P}\right]=D^{\alpha }\hat{P}$$ (A.2)

with $L_{\alpha }\left[A\right]=0$, where $A$ is the integration constant, which is determined by the initial conditions.

If $q\in [0,1]$ and $h$ indicate the embedding and non-zero auxiliary parameters, respectively, then the zero-order deformation problems are of the following form:

$$(1-q)L_{\alpha }[\hat{N}(t;q)-N_0\left(t\right)]=qh{B}_N[\hat{N}(t;q),\hat{P}(t;q)]$$$$(1-q)L_{\alpha }[\hat{P}(t;q)-P_0\left(t\right)]=qh{B}_P[\hat{N}(t;q),\hat{P}(t;q)]$$ (A.3)

subject to the initial conditions

$$\hat{N}(0;q)=c_1\text{,}\hat{P}(0;q)=c_2$$

in which we define the nonlinear operators $B_N$ and $B_P$ as

$$B_N[\hat{N}(t;q),\hat{P}(t;q)]=\frac{{\partial }^{\alpha }\hat{N}(t;q)}{\partial t}-r\hat{N}(t;q)(1-\frac{\hat{N}(t;q)}{K})+k\hat{P}(t;q)(1-e^{-c\hat{N}(t;q)})$$$$B_P[\hat{N}(t;q),\hat{P}(t;q)]=\frac{{\partial }^{\alpha }\hat{P}(t;q)}{\partial t}-Ak\hat{P}(t;q)(e^{-cJ}-e^{-c\hat{N}(t;q)})\text{.}$$ (A.4)

For $q=0$ and $q=1$, zero-order (A.3) have the solutions

$$\hat{N}(t;0)=N_0\left(t\right)\text{,}\hat{P}(t;0)=P_0\left(t\right)$$

and

$$\hat{N}(t;1)=N\left(t\right)\text{,}\hat{P}(t;1)=P\left(t\right)\text{.}$$

When $q$ increases from 0 to 1, then $\hat{N}(t;q)$ and $\hat{P}(t;q)$ vary from $N_0\left(t\right)$ and $P_0\left(t\right)$ to $N\left(t\right)$ and $P\left(t\right)$, respectively.

Expanding $\hat{N}$ and $\hat{P}$ in Taylor series with respect to $q$, we have

$$\hat{N}(t;q)=N_0\left(t\right)+\sum _{m=1}^{\infty }{N}_m\left(t\right)q^m$$$$\hat{P}(t;q)=P_0\left(t\right)+\sum _{m=1}^{\infty }{P}_m\left(t\right)q^m$$ (A.5)

in which $N_m\left(t\right)={\frac{1}{m!}\frac{{\partial }^m\hat{N}(t;q)}{\partial q^m}|}_{q=0},P_m\left(t\right)={\frac{1}{m!}\frac{{\partial }^m\hat{P}(t;q)}{\partial q^m}|}_{q=0}$

$$N\left(t\right)=N_0\left(t\right)+\sum _{m=1}^{\infty }{N}_m\left(t\right)$$$$P\left(t\right)=P_0\left(t\right)+\sum _{m=1}^{\infty }{P}_m\left(t\right)\text{.}$$ (A.6)

We take the $m$th-order homotopy derivative of the zero-order (A.3) and use  [67, Properties 1–5] to obtain the $m$-order deformation equations

$$L_{\alpha }[N_m\left(t\right)-{\chi }_m{N}_{m-1}\left(t\right)]=h{R}_m^N\left(t\right)$$$$L_{\alpha }[P_m\left(t\right)-{\chi }_m{P}_{m-1}\left(t\right)]=h{R}_m^P\left(t\right)$$ (A.7)

with the initial conditions

$$N_m\left(0\right)=0\text{,}{P}_m\left(0\right)=0\text{,}$$ (A.8)

where

$$R_m^N\left(t\right)=D^{\alpha }{N}_{m-1}-r{N}_{m-1}+\frac{r}{K}\sum _{i=0}^{m-1}{N}_i{N}_{m-1-i}+k{P}_{m-1}-k\frac{e^{-c{N}_0}}{m!}\sum _{l=0}^m\left(\begin{array}{c}\hfill m\hfill \\ \hfill l\hfill \end{array}\right){\varphi }_1^{\left(l\right)}{\varphi }_2^{(m-l)}$$$$R_m^P\left(t\right)=D^{\alpha }{P}_{m-1}-Ak{e}^{-cJ}{P}_{m-1}+Ak\frac{e^{-c{N}_0}}{m!}\sum _{l=0}^m\left(\begin{array}{c}\hfill m\hfill \\ \hfill l\hfill \end{array}\right){\varphi }_1^{\left(l\right)}{\varphi }_2^{(m-l)}$$ (A.9)

${\varphi }_1={\sum }_{m=1}^{\infty }{P}_{m-1}{q}^m,{\varphi }_2=e^{-c{\sum }_{m=1}^{\infty }{N}_m{q}^m}$ and ${\varphi }_1^{\left(l\right)}=\frac{{\partial }^l{\varphi }_1}{\partial q^l}{|}_{q=0}$ and ${\chi }_m=\{\begin{array}{cc}0& \text{if }m\le 1\\ 1& \text{if }m>1\end{array}$.

In this way, it is easy to solve the linear non-homogeneous equations (A.7) with initial conditions (A.8) for all $m\ge 1$ and we obtain

$$N_1\left(t\right)=[-r{c}_1+\frac{r{c}_1^2}{K}+k{c}_2-c_2{e}^{-c{c}_1}]\frac{h{t}^{\alpha }}{\Gamma (\alpha +1)}$$

$$P_1\left(t\right)=[-Ak{c}_2{e}^{-cJ}+Ak{c}_2{e}^{-c{c}_1}]\frac{h{t}^{\alpha }}{\Gamma (\alpha +1)}$$

$$N_2\left(t\right)=h(1+h)[-r{c}_1+\frac{r{c}_1^2}{K}+k{c}_2-c_2{e}^{-c{c}_1}]\frac{t^{\alpha }}{\Gamma (\alpha +1)}+h^2[(-r+\frac{2r{c}_1}{K}-c{c}_{2}k{e}^{-c{c}_1})(-r{c}_1+\frac{r{c}_1^2}{K}+k{c}_2-c_2{e}^{-c{c}_1})+k(1-e^{-c{c}_1})(-Ak{c}_2{e}^{-cJ}+Ak{c}_2{e}^{-c{c}_1})]\frac{t^{2\alpha }}{\Gamma (2\alpha +1)}$$

$$P_2\left(t\right)=h(1+h)[-Ak{c}_2{e}^{-cJ}+Ak{c}_2{e}^{-c{c}_1}]\frac{h{t}^{\alpha }}{\Gamma (\alpha +1)}+h^2[A^2{k}^2{c}_2{(e^{-cJ}-e^{-c{c}_1})}^2-Ak{c}_2{e}^{-c{c}_1}(-r{c}_1+\frac{r{c}_1^2}{K}+k{c}_2-c_2{e}^{-c{c}_1})]\frac{t^{2\alpha }}{\Gamma (2\alpha +1)}\text{.}$$

Proceeding similarly, the $p$th term of the approximate solutions of (3.2) is

$$N\left(t\right)=N_0\left(t\right)+\sum _{m=1}^p{N}_m\left(t\right)$$$$P\left(t\right)=P_0\left(t\right)+\sum _{m=1}^p{P}_m\left(t\right)\text{.}$$ (A.10)

Appendix B.

This appendix provides the conditions for which our fractional Rosenzweig model is stable.

$$D^{\alpha }N\left(t\right)=rN(1-\frac{N}{K})-kP(1-e^{-c(1-m)N})$$$$D^{\alpha }P\left(t\right)=AkP(e^{-cJ}-e^{-c(1-m)N})\text{,}$$ (B.1)

where $m\in [0,1)$ is the refuge parameter. The interior equilibrium point of model (B.1) is $N^{\ast }=\frac{J}{1-m},P^{\ast }=\frac{r{N}^{\ast }(1-\frac{N^{\ast }}{K})}{k(1-e^{-cJ})}$. The corresponding variational matrix is

$$V=\left(\begin{array}{cc}\hfill r-\frac{2r{N}^{\ast }}{K}-kc(1-m)P^{\ast }{e}^{-cJ}\hfill & \hfill -k(1-e^{-cJ})\hfill \\ \hfill Akc(1-m)P^{\ast }{e}^{-cJ}\hfill & \hfill 0\hfill \end{array}\right)\text{.}$$

The fractional counterpart of model (B.1) is locally asymptotically stable if

$$\left|arg\left({\lambda }_i\right)\right|>\frac{\alpha \pi }{2}\text{,}i=1,2\text{,}$$ (B.2)

where ${\lambda }_1,{\lambda }_2$ are the eigenvalues of the Jacobian matrix $V$ and $\alpha (0<\alpha \le 1)$ is the order of the fractional derivative.

Appendix C.

Parameter estimation and sensitivity analysis

We estimated the parameters of our fractional Rosenzweig model and analyzed its sensitivity with respect to $\alpha$.

To estimate the parameters we used the total least squares method  [68], [69], also known as orthogonal distance fitting (ODF), which has significant advantages  [70] in the case of several spatial dimensions. ODF uses perpendicular (orthogonal) distances between given points and the fitting curve. The sum of orthogonal distances between two sets of points is described by ${\sum }_{i=1}^n{\left[d((x_i,y_i),f({\alpha }_1,{\alpha }_2,\dots ,{\alpha }_n))\right]}^2$, where $n$ is the number of experimental points and the parameters ${\alpha }_1,{\alpha }_2,\dots ,{\alpha }_n$ influence the function $f$, which is called the fitting curve or the set of fitting points; $d$ represents the distance from given experimental points, with coordinates $(x_i,y_i)$, to the fitting curve $f$. We used the fmincon optimization algorithm in MATLAB for data fitting of model (3.2) as described by Skovranek et al.  [71].

The coordinates of the points to be fitted in the state space are generated randomly in 2D space. We generated an initial data set of 30 points from model (3.2) with the parameter values listed in Table 1, along with $K=20$ and $\alpha =0.75$. The final data set was generated by adding Gaussian noise to the data set for each predator–prey population with variance of 0.1 and 0.6 for prey and predator populations, respectively. Fig. 6 shows the results, in which the green points are randomly generated and the red line represents the estimated curve. The estimated model parameters and error of fit using the fmincon procedure are given in Table 2 .

Table 2.

Estimated parameter values.

$\alpha$	$r$	$k$	$c$	$A$	$J$	$K$	Error of fit
0.7893	0.1	0.1	0.0598	1.812	21.0428	17.2995	43.2420

Fig. 6.

Phase-plane diagram of the trajectory of predator–prey density based on 30 selected points (green circles) generated through simulation with Gaussian noise added to the fractional Rosenzweig model (3.2). The red line shows the fitting curve for the simulated data. Parameter values were taken from Table 1, along with $K=20$ and $\alpha =0.75$, to generate the data. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

We conducted a sensitivity analysis of model (3.2) with respect to $\alpha$. We used the sensitivity coefficient proposed by Loucks et al. for our analysis  [72]. This measures the magnitude of change in an output variable $Q$ per unit change in the magnitude of an input parameter value $\alpha$ from its base value ${\alpha }_0$. We used the sensitivity coefficient  [73] $S_{\alpha }=max\{|(Q_0-Q_i)/({\alpha }_0-{\alpha }_i)|,|(Q_0-Q_j)/({\alpha }_0-{\alpha }_j)|\}$ and calculated the elasticity index  [72], [73] $E_{\alpha }=\left[\frac{{\alpha }_0}{Q\left({\alpha }_0\right)}\right]S_{\alpha }$, which is a dimensionless sensitivity measure of the relative change in output $Q$ for a relative change in input $\alpha$. Here the index $i$ represent a decrease and $j$ an increase in the parameter from its base value ${\alpha }_0$.

For model (3.2) we calculated the elasticity index with respect to input variable $\alpha$. The output$\left(Q\right)$ is the range of $K$ up to which the system is stable. We calculated the output $\left(Q\right)$ for values of $\alpha$ from 0.4 to 1 and then calculated the elasticity index and plotted this as a function of $\alpha$ in Fig. 7 . It is clear that the elasticity index increases as $\alpha$ decreases. It should be noted that enrichment does not hold for values less than a threshold of $\alpha =0.2332$, so the range $\alpha \in [0.4,1]$ is used in Fig. 7.

Fig. 7.

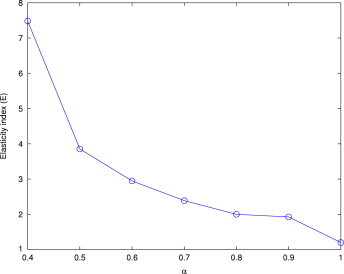
Variation of the elasticity index for $\alpha$ as an input variable and a specified range of $K$ as the output variable. Other parameter values are taken from Table 1.