Extending statistical learning for aneurysm rupture assessment to Finnish and Japanese populations using morphology, hemodynamics, and patient characteristics

Abstract

Object

Incidental aneurysms pose a challenge for physicians who need to weigh the rupture risk against the risks associated with treatment and its complications. A statistical model could potentially support such treatment decisions. We recently developed an aneurysm rupture probability model that performs well in the US data used for model training and two external European cohorts. Japanese and Finnish patients are known to have a higher aneurysm rupture risk. Our goal was to evaluate this model in data from Japanese and Finnish patients and compare it with new models trained with Finnish and Japanese data.

Methods

Patient and image data of 2129 aneurysms in 1472 patients were used. Of these aneurysm data, 1631 had been collected mainly in US hospitals, 249 in European (other than Finnish), 147 in Japanese, and 102 in Finnish hospitals. Computational fluid dynamics simulations and shape analysis were conducted to quantitatively characterize each aneurysm’s shape and hemodynamics. Next, the previously developed model’s discrimination was evaluated in the Finnish and Japanese data in terms of area under the receiver operating characteristic (ROC) curve (AUC). Models with and without interaction terms between patient population and aneurysm characteristics were trained and evaluated including data from all four cohorts obtained by repeatedly randomly splitting the data into training and test data.

Results

The US-model’s AUC was reduced to 0.70 and 0.72 in the Finnish and Japanese data compared to 0.82 and 0.86 in the European and US data. When training models with Japanese and Finnish data, the average AUC increased only slightly for the Finnish sample (to 0.76±0.16) and Finnish and Japanese cases combined (from 0.74 to 0.75±0.14), and decreased for the Japanese data (to 0.66±0.32). In models including interaction terms, the AUC in the Finnish and Japanese data combined increased significantly to 0.83±0.10.

Conclusions

Development of an aneurysm rupture prediction model that applies to Japanese and Finnish aneurysms requires including data from these two cohorts for model training as well as interaction terms between patient population and the other variables. When including this information, the performance of such a model in Japanese and Finnish data is close to its performance in US or European data. These results suggest that population-specific differences determine how hemodynamics and shape associate with rupture risk in intracranial aneurysms.

Introduction

Intracranial aneurysms (IAs) are a common vascular pathology, affecting about 2–3% of the population.^18,21 Most of the IAs remain asymptomatic and do not cause any medical complications. However, in case of an aneurysm rupture, the patient suffers from subarachnoid hemorrhage (SAH), which is associated with high mortality, morbidity as well as a large economic burden.^19,22 Due to an increased use of medical imaging for diagnostics of various diseases, a rising number of IAs is incidentally diagnosed. In these cases, physicians face the challenge of having to decide whether treat the patient or conservatively follow-up the IA since the risk associated with interventions aiming at preventing a future aneurysm rupture outweighs the natural aneurysm rupture risk.^12,20,24

The pathophysiological mechanisms leading to aneurysm rupture are not yet fully understood. A plethora of risk factors has been suggested in the literature.¹³ These risk factors include patient-related aspects like patient gender or smoking status, genetics, geometric factors describing the shape of an IA, and hemodynamic factors. Hemodynamics are believed to play an important role in aneurysm development, growth, and rupture through biomechanical signaling processes in the vessel wall.^3,16 Several risk scores for aneurysm growth or rupture have been published to support physicians in decision making.^2,10,11 These scores are mainly based on patient characteristics and for a specific IA, only take its location, size, and “irregularity” defined either simply as “irregular shape”² or “irregularity or lobulation”¹⁰ into account. While the classification of the shape as simple or irregular is highly subjective, aneurysm hemodynamics are not considered at all. To overcome this limitation, we recently developed an aneurysm rupture probability model taking hemodynamic, geometric, and patient-related factors into account.⁶ The model had been developed using data from 1,631 aneurysms obtained mainly from hospitals in the US. When evaluating the model in two external European cohorts, it showed a good predictive performance, indicating that it generalizes to patient cohorts other than the one used for model training.⁷

The results of several studies suggest that Finnish and Japanese have a higher risk of aneurysmal SAH compared to other populations.^11,23 Comparison of aneurysm-related and patient-related characteristics in these two high risk populations with aneurysms and patients in other populations can give insight into what causes the higher risk of aneurysmal SAH in the Finnish and Japanese. This knowledge is likely to increase our overall understanding of the development and progression of the disease. The aim of this study was therefore to evaluate in Japanese and Finnish aneurysm patients the rupture probability model originally developed from US derived data. Furthermore, that model was compared to a new model being trained on data including parts of the Finnish and Japanese as well as European (other than Finnish) data. Finally, the models’ performances were compared to a similarity-based approach, where similar aneurysms from our database (US + European) were identified to classify a new Japanese or Finnish aneurysm’s rupture status.⁷

Methods

Patient and Image Data

This study is based on four aneurysm datasets. For the remainder of this paper, they will be referred to as “US”, “European” (short for “European other than Finnish”), “Finnish”, and “Japanese”. All four datasets include patient information (patient gender and age), as well as 3D images (three dimensional rotational angiography (3DRA; US, European and Finnish cohorts) or computed tomography angiography (CTA; Japanese cohort)) of the respective aneurysm and surrounding vasculature. The US data were collected from hospitals mainly in the US and include 1631 aneurysms from 1061 patients. Details of the dataset can be found in Detmer et al.⁶ The two European (other than Finnish) cohorts including in total 249 aneurysms from 203 patients were the AneuX dataset and the publicly available AneuRisk dataset (see Detmer et al.⁷ for details). The Finnish dataset consisted of 102 IAs in 71 patients treated at Kuopio University Hospital. All the US, European, and Finnish data were cross-sectional data, for which the aneurysm rupture status was defined as the rupture status at the time of presentation of the patient at the hospital. In contrast, the Japanese dataset including data of 255 aneurysms in 147 patients consisted of longitudinal data where the aneurysm rupture status was defined after a mean follow-up time of 900.8 days in case of the ruptured aneurysms (all ruptures occurred during follow-up) and 2432.1 days of aneurysms classified as unruptured. The images that were used for hemodynamic and shape characterizations were obtained before and close to the rupture for ruptured cases. We used the newest images for the unruptured cases.

Table 1 shows a comparison of patient and aneurysm characteristics between the four populations.

Table 1.

Summary of patient characteristics and distribution of aneurysm location in the cerebral vasculature for the four data sets.

		US (Training population of original model)	European	Japanese	Finnish
Number of patients		1061	203	137	71
Number of aneurysms (ruptured/unruptured)		1631 (492R/1139U)	249 (66R/183U)	147 (17R/130U)	102 (41R/61U)
Patient age (mean ± sd) (of 1065 patients with known age)		56.25±13.77	54.68±13.61	69.11±10.99	53.07±11.70
Patient with multiple aneurysms		329	35	10	28
Number of patients with SAH		490	66	16	41
Aneurysm location	ACA	57 (3.49%) 20R/37U	5 (2.00%) 2R/3U	2 (1.36%) 1R/1U	6 (5.88%) 4R/2U
	ACOM	226 (13.86%) 148R/78U	45 (18.07%) 23R/22U	30 (20.41%) 3R/27U	21 (20.59%) 14R/7U
	BA	106 (6.50%) 35R/71U	14 (5.62%) 7R/7U	6 (4.08%) 1R/5U	7 (6.86) 7R/0U
	ICA	636 (38.99%) 64R/572U	77 (30.92%) 5R/72U	15 (10.20%) 1R/14U	21 (20.59%) 4R/17U
	MCA	310 (19.01%) 82R/228U	71 (28.51%) 14R/57U	54 (36.73%) 7R/47U	34 (33.33%) 13R/21U
	PCOM	260 (15.94%) 127R/133U	33 (13.25%) 14R/19U	40 (27.21%) 4R/36U	11 (10.78%) 4R/7U
	VA	36 (2.21%) 16R/20U	4 (1.61%) 1R/3U	0 (0%) 0R/0U	2 (1.96%) 2R
Gender		802 F, 259 M	144 F, 59 M	80 F, 57 M	39 F, 32 M

ACA=anterior cerebral artery, ACOM=anterior communicating artery, BA=basilar artery, ICA=internal carotid artery, MCA=middle cerebral artery, PCOM=posterior communicating artery, VA=vertebral artery

Hemodynamic Modeling and Shape Characterization

From the US and Finnish images, the aneurysms and surrounding vasculatures were segmented with in-house software based on a thresholding approach, the AneuX images had been segmented with a geodesic active regions method integrated in the @neuFuse software and a level set–based approach implemented in Matlab, and the AneuRisk image segmentations had been generated using the “Vascular Modeling ToolKit” (VMTK) with a gradient-driven level set approach.⁷ For the Japanese images, Amira 5.6 (FEI/VSF-division, Bordeaux, France) was used with a thresholding method.

After vessel lumen segmentation, computational meshes of tetrahedral elements with a maximum size of 0.2 mm were obtained with in-house software for subsequent computational fluid dynamics (CFD) simulations.⁴ Next, the unsteady Navier-Stokes equations were numerically solved with an in-house finite element solver for two cardiac cycles of 60 beats per minute. Inlet and outlet boundary conditions were set as pressure and flow in-/outlets as previously described.⁶ For all datasets but the Japanese, inlet boundary conditions were either imposed at the internal carotid artery for IAs located at the anterior circulation or the vertebral artery for IAs of the posterior circulation. For the Japanese models, inflow boundary conditions were imposed at the IA’s respective parent vessel.

The results of the second cardiac cycle were used for characterization of the aneurysm’s hemodynamic environment by 22 hemodynamic parameters capturing flow complexity, concentration, instability and wall shear stress (WSS) distribution.⁶ The generated computational meshes were further used for aneurysm shape characterization quantified by 25 geometric parameters describing the aneurysm size, elongation, sphericity, and irregularity.⁶

Model Evaluation and Comparison

Based on the computed hemodynamic and morphological parameters, as well as aneurysm location in the cerebral vasculature and patient gender and age, the rupture probability model (later also referred to as “US-model” because of its training cohort)⁶ was used to compute the predicted probability of being ruptured for each of the Japanese and Finnish aneurysms. Subsequently, the model’s discriminative power was evaluated in terms of area under the receiver operating characteristic curve (AUC) for the Japanese, Finnish, and combined Finnish and Japanese datasets, respectively.

Next, this study aimed at assessing whether the model performance in the Japanese and Finnish population could potentially be improved by including data from these two cohorts for model training. The datasets were split into model training and test data. For each of the four populations, 10% of the data were randomly excluded and a model including the same variables as the previously developed rupture probability model was trained on the remaining data using logistic group lasso regression.¹⁵ The procedure of random data splitting and model fitting was repeated 100 times and mean and standard deviation of the AUC when evaluated in the left-out data were reported. As the aneurysm rupture risk varies for Finnish and Japanese patients compared to other populations, we hypothesized that the effect of certain hemodynamic as well as geometric parameters or patient characteristics on the rupture risk might vary by population. Therefore, following the same procedure as described above, we also fitted models including interaction terms between hemodynamic, geometric, and patient age and gender variables and the variable “patient population”. Such a model interpolates between a global model and a separate model for each population.

Identification of Similar Cases

Although the logistic regression rupture probability model has a “simple” quantitative outcome when applied to a new case (the predicted probability of being ruptured), the interpretation of the model itself and all its parameters can be difficult. Therefore, as for our external validation of the model with the two European cohorts,⁷ we assessed the performance of rupture status classification alternatively based on “similar” cases in our database. To apply this approach to the Japanese and Finnish cohorts, similar cases from the combined US and European datasets were defined as IAs with comparable values in maximum oscillatory shear stress (OSImax), non-sphericity index (NSI), aneurysm size (Asize), mean surface curvature (MLN), and being located at the same position in the cerebral vasculature. OSImax, NSI, and aneurysm location had previously been identified as important variables for discrimination of aneurysm rupture status.⁶ We further added MLN in this study, since this parameter was one of the most frequently included parameters in the repeatedly fitted models while at the same time interactions between patient population and MLN were included in none of the models. This finding indicates that MLN has an influence on the aneurysm rupture status which does not vary by patient population. The latter aspect was important since we used similar US and European IAs to predict the rupture status of Finnish and Japanese IAs. Aneurysm size was included to capture the IA’s current phase of evolution. Details of the definition of rupture status and the exact definition of similar cases can be found in Detmer et al.⁷

All statistical data processing was performed with scripts written in the R language.¹⁷

Results

Table 2 and Fig. 1 show the AUCs when evaluating each of the three categories of models – the previously developed model using the US data (US-model, black squares in Fig. 1), the model including Japanese and Finnish aneurysms in the training data without and with interaction terms (white and grey bars, respectively). When evaluating the US-model in the Finnish and Japanese data, the AUCs were 0.72 and 0.70, respectively, which was considerably lower compared to the model’s performance in the European cohorts (AUC of 0.82). Fig. 2 (left) compares the ROC curves of the US-model for each of the populations, also illustrating its comparatively low performance in the Finnish and Japanese data. The model further seems to be mis-calibrated for these two populations as indicated by the calibration plot on the right of Fig. 2. For a perfectly calibrated fit, all into deciles grouped outcomes (geometric shapes in Fig. 2) as well as the loess smoothers (solid and dotted lines; fitted with a span parameter of 0.751) would lie on the 45-degree line. The US-model is well calibrated for the training data (solid line) and similarly for the external European data (large dotted line).

Table 2.

Results of model fitting and evaluation for the US-model⁶ and re-trained models including data from all four populations without and with interaction terms.

Model Type	Training Data	AUC training (mean ± SD)	Test Data	AUC test (mean ± SD)
US-Model	US (n=1631)	0.8553	EUR (n=249)	0.8240
			JAP (n=147)	0.6964
			FIN (n=102)	0.7209
			FIN, JAP (n=249)	0.7389
No interactions	All (n=1914)	0.8493 ± 0.0059	Left-out US, EUR, FIN, JAP (n=215)	0.8268 ± 0.0323
			Left-out JAP (n=15)	0.6550 ± 0.3334
			Left-out FIN (n=11)	0.7550 ± 0.1646
			Left-out FIN, JAP (n=26)	0.7494 ± 0.1371
Interactions	All (n=1914)	0.8681 ± 0.0091	Left-out US, EUR, FIN, JAP (n=215)	0.8308 ± 0.0309
			Left-out JAP (n=15)	0.6576 ± 0.3199
			Left-out FIN (n=11)	0.8020 ± 0.1324
			Left-out FIN, JAP (n=26)	0.8274 ± 0.1031

US=aneurysm data from the US, JAP=aneurysm data from Japan, FIN=aneurysm data from Finland. EUR=aneurysm data from Europe without Finland. “All” refers to data from all four populations without the excluded data for testing.

Figure 1.

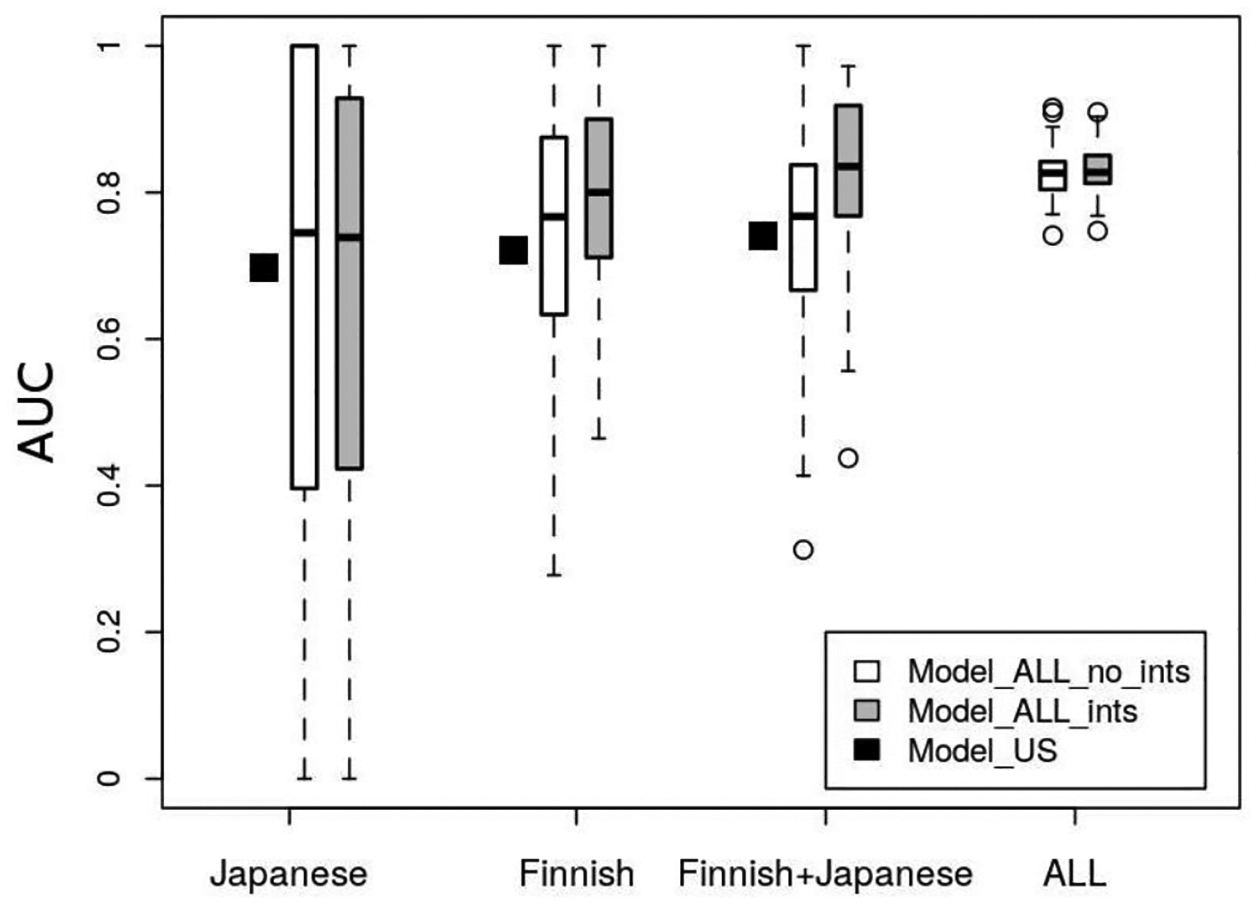
Boxplots showing the AUCs of the repeatedly fitted models when evaluated in the Japanese, Finnish, Finnish and Japanese combined and all left-out data.

Figure 2.

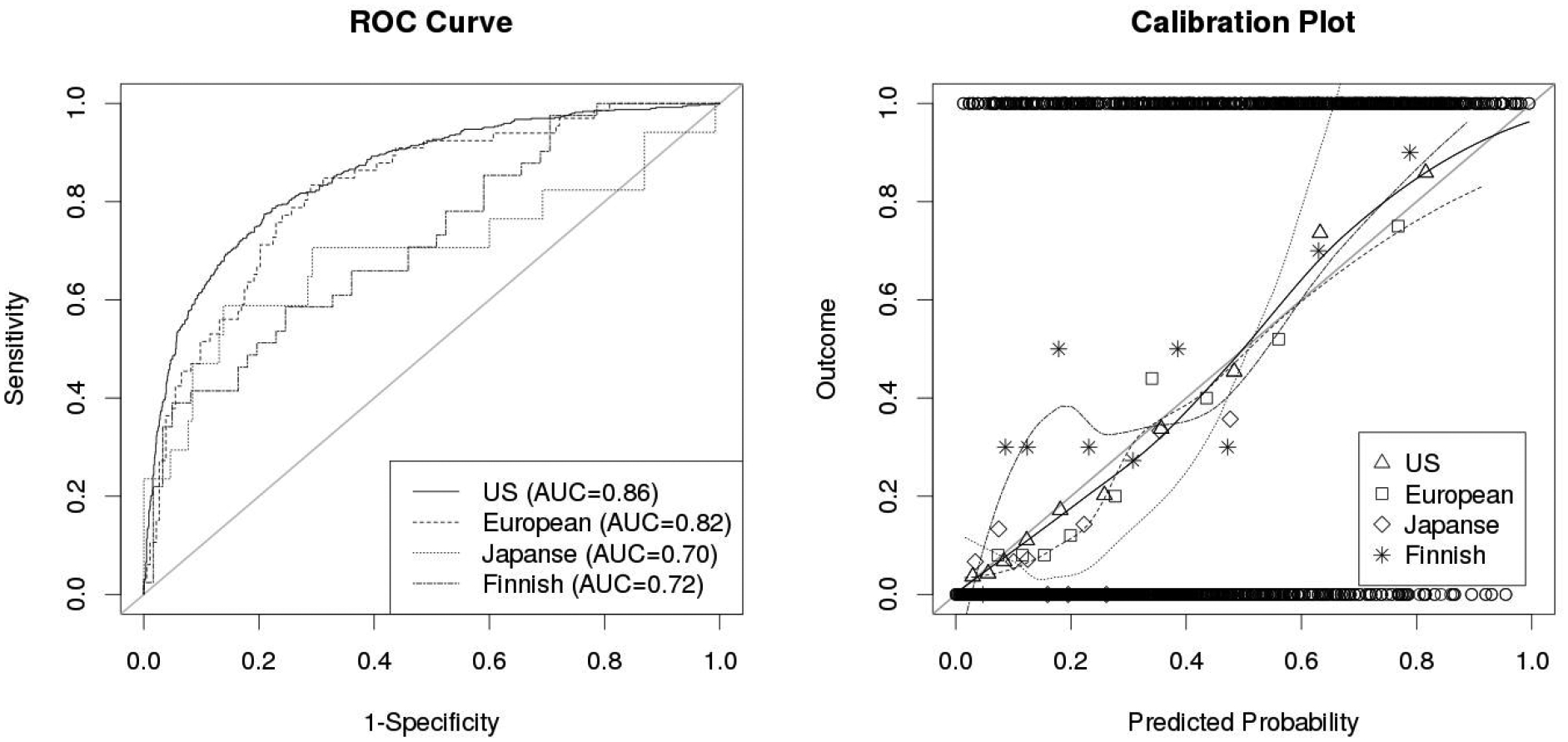
ROC-curves (left) and calibration plots (right) of the US model for the US training data and the external European, Finnish, and Japanese cohorts. ROC curves illustrate the discrimination of a model, calibration plots allow to assess its goodness-of-fit. The circles at the top and bottom of the calibration plot show the observed data. The geometric shapes show the observed outcomes of the training and test populations grouped by deciles, which are also represented by the loess smoother with the solid and dotted lines. For a perfectly calibrated fit, all geometric shapes and the loess smoother would lie on the 45°-line

When re-training the model using a subset of data from all four cohorts, the AUC of the models in the Japanese data decreased on average to 0.66 (± 0.33), for the Finnish IAs, it increased to 0.76 (± 0.16). For the models including interaction terms, the mean AUC remained almost the same for the Japanese cohort (0.66 ± 0.32), but increased largely for the Finnish data (0.80 ± 0.13) and the Finnish and Japanese data combined (0.83 ± 0.10). In all the left-out data combined, the AUCs were 0.83 ± 0.03 for the model without interactions and 0.83 ± 0.03 for the models including interactions.

Features that were most frequently (≥ 99%) included for the re-fitted models without interactions were patient gender and age, aneurysm kinetic energy (KE), low shear area (LSA), OSImax, height-to-width ratio (HWR), bulge location (BL), volume-to-ostium ratio (VOR), non-sphericity index (NSI), MLN, and aneurysm location. For the models including interaction terms, the most frequently included parameters were patient age, gender and population¹, KE, LSA, OSImax, HWR, BL, NSI, MLN, mean Gaussian curvature (GLN), aneurysm location, as well as interactions between patient population and aneurysm neck area (Narea), mean OSI (OSImean), area weighted average of Gaussian curvature (GAA) and patient gender.

When using similar aneurysms from the European and US populations for classifying Finnish and Japanese aneurysms as ruptured or unruptured as defined above, 70.59 % of the Finnish aneurysms were correctly classified and 81% of the Japanese aneurysms. The true-positive-rate and false-positive-rate were 0.5122 and 0.1639 for the Finnish, and 0.3529 and 0.1308 for the Japanese data.

Discussion

The treatment decision for incidentally diagnosed IAs poses a challenge for physicians who need to weigh the interventional risk against the risk of a potential aneurysmal SAH. A statistical model could support these treatment decisions. An essential requirement for such a model is generalizability to patient cohorts other than the one that had been used for model training. Japanese and Finnish cohorts have a higher aneurysm rupture risk compared to other populations.^11,23 The underlying mechanisms of this finding are not completely understood yet. With our work, we aimed at evaluating whether our model, trained on US and validated in European data, would also be applicable to Finnish and Japanese patients. Our results suggest that the relative importance of hemodynamics, aneurysm morphology, and patient related factors for the eventual risk of rupture differs in aneurysms from the Finnish and Japanese populations, indicating that other environmental or genetic factors cause the increased risk of aneurysmal SAH observed in these two populations. Moreover, our findings demonstrate how rupture-probability models for intracranial aneurysms need to be adjusted to specific populations.

Model Performance

We observed that the model’s performance was largely reduced in the Finnish and Japanese data, revealed by the comparatively low AUC (0.74 for Finnish and Japanese combined) and relatively poor calibration. This finding indicates that different IA characteristics might be associated with rupture for these two populations compared to US and European cohorts. This hypotheses is further supported by our observation that simply including data from Finnish and Japanese patients in the training data, did not largely improve the performance (AUC changed from 0.74 to 0.75 on average), but increased significantly (p<0.0001, t-test) when including interaction terms of the hemodynamic, geometric, and patient-related parameters with patient population into the model. Interaction terms that were most frequently included in the fitted models were interactions with Narea, OSImean, GAA, and patient gender. Why particularly these variables seem to have a different effect on IA rupture status depending on the patient’s population, needs to be explored further in future. Possible explanations include different genetic background that would affect the mechanobiological coupling of hemodynamic factors and vessel wall remodeling, or population-related differences in environmental or other acquired factors that predispose to aneurysm rupture and may explain why aneurysms that would not rupture in other populations would rupture in Finns or Japanese.

Other important variables (without interaction terms) included patient age, gender and population, KE, LSA, OSImax, HWR, BL, NSI, MLN, mean Gaussian curvature (GLN), and aneurysm location. The association particularly of NSI and LSA with IA rupture status is consistent with previous studies.^8,9,14,27

The poor average performance of all the models in the Japanese data only (not combined with Finnish) could in part be potentially explained by several technical aspects. First, in contrast to the data from the other patient cohorts, the computational 3D models used for the CFD simulations of the Japanese IAs were cut at the parent vessel of the IA. This might have led to differences in the computed hemodynamics and needs to be assessed further. This issue is not expected to largely affect the similarity-based approach, which performed well in the Japanese dataset, since it is mainly based on geometric parameters.

Second, unlike the data for the other populations, the Japanese data were longitudinal data obtained by following up patients for a certain time. Consequently, the dataset contained a low number of ruptured IAs, particularly in the left-out test datasets for the repeatedly fitted models. This aspect also explains the large variation of discrimination power for the different left-out datasets (standard deviation of 0.32, range between 0 and 1) meaning that the observed AUC was largely influenced by the fact which particular ruptured IA(s) were included in the dataset for evaluation. When combining the Japanese and Finnish left-out data for model evaluation, the mean AUC increased to 0.83 and the standard deviation was reduced to 0.10. For a robust estimation of the models’ performance in Japanese IAs, a larger dataset might hence be needed.

For evaluating the fitted models trained using data from all four populations, a split-sample approach was used since no fully external data were available at this point. Hence, the predictive performance of the fitted models needs to be confirmed in future with a larger, external data set.

Still, the good performance in the Japanese and Finnish left-out data combined provides some support to the idea that statistical models based on hemodynamic, morphological and patient data could improve assessment of a future aneurysm rupture risk since the Japanese dataset was longitudinal (based on follow-up data).

Aneurysm Rupture Status Classification based on Similar Cases

The identification of similar IAs for classification of a new IA’s rupture status achieved good results with accuracies of 71% in the Finnish and 81% in the Japanese cohorts. The models and OSI distributions of four examples are illustrated in Fig. 3. Additional flow characteristics (WSS, inflow jets, and streamlines) of the eight aneurysms are shown in Fig. 4 and 5. Aneurysms a and c are Finnish aneurysms for which similar cases b and d were identified from the US and European datasets by the algorithm described above. For the two Japanese aneurysms e and g, the similar cases f and h were matched. All “similar” aneurysms have a comparable shape and OSI distribution. Values of selected parameters for these eight aneurysms are shown in Table 3. The Finnish/Japanese and their respective US/European cases had by definition close values in NSI, OSImax, MLN, and Asize. Furthermore, they had overall similar predicted probabilities of being ruptured based on the US-model. Interestingly, aneurysm g had – consistent with its rupture status – a lower probability of 26% of being ruptured compared to the four ruptured cases despite being relatively large and located at the ACOM, which are characteristics typically associated with high-risk aneurysms. Thus, it presents a case where an aneurysm that might intuitively be thought of as high risk could actually be a low-risk aneurysm (this aneurysm remained unruptured during longitudinal follow-up), which is correctly detected by the model. Consistently, it was also matched with an unruptured IA. The similarity-based approach could potentially be improved by taking other IA characteristics into account. For example, the configuration of the IAs’ parent arteries is not considered, which has an influence of the inflow into the aneurysm. Additionally, similarity in terms of flow was only captured by OSImax, resulting e.g. in different WSS distribution for some of the cases (see WSS distribution of g and h in Fig. 5). The good performance in the Japanese data might partly also result from the low number of ruptured aneurysms and needs to be explored further with data from more aneurysms in future.

Figure 3.

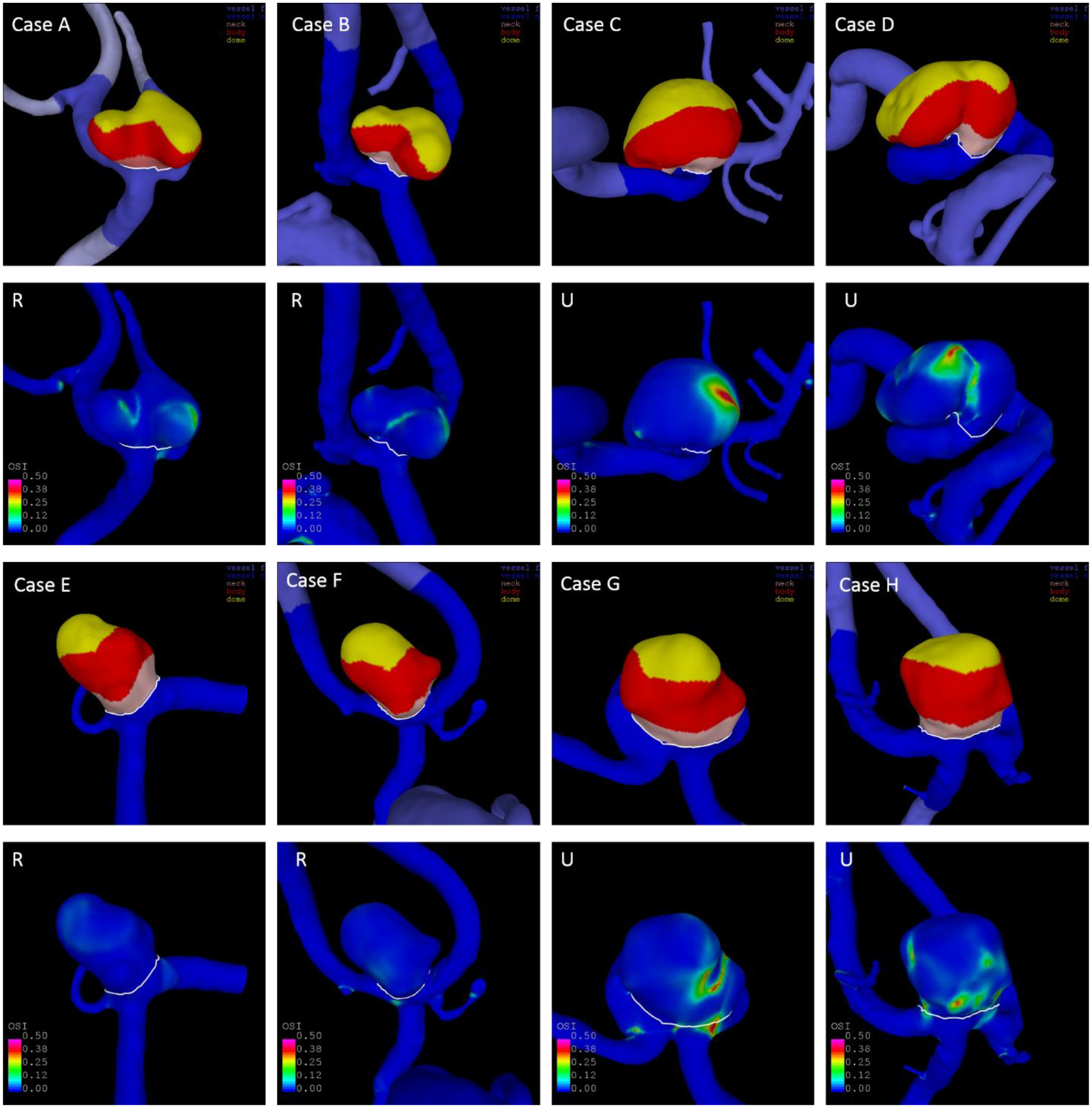
Computational models showing the aneurysm’s shape (1st and 3rd row) and OSI distribution (2nd and 4th row) of two aneurysms from Finnish patients (a and c), two from Japanese patients (e and g) and their respective similar cases from the US-European cohorts (b, d, f, h). The four aneurysms on the left are ruptured, the four aneurysms on the right unruptured. Values of selected parameters of all eight cases are shown in Table 3.

Figure 4.

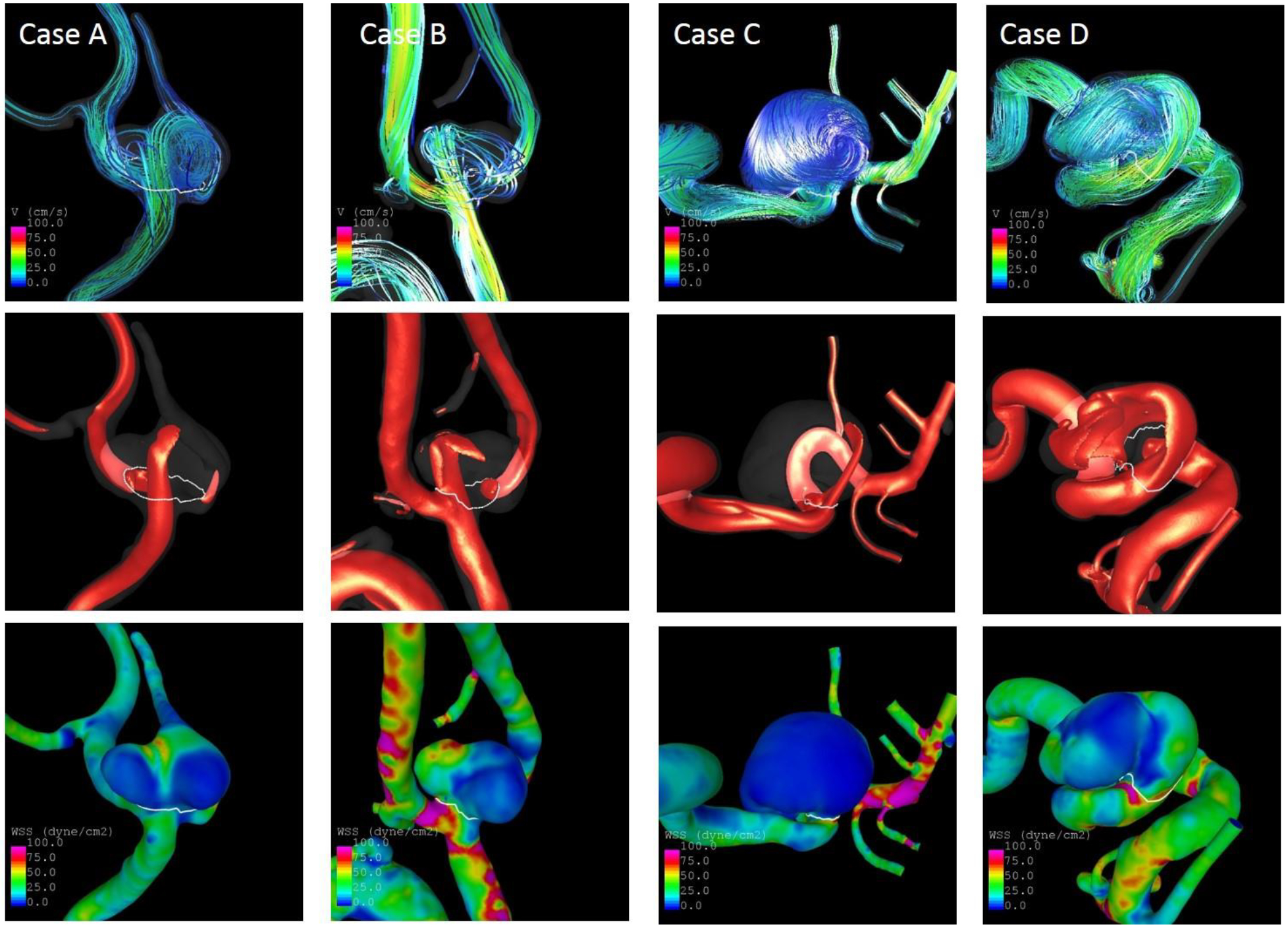
Streamlines (top), inflow jets (middle) and WSS distribution (bottom) at half of the cardiac cycle of the two Finnish aneurysms (a, c) and their similar cases (b, d)

Figure 5.

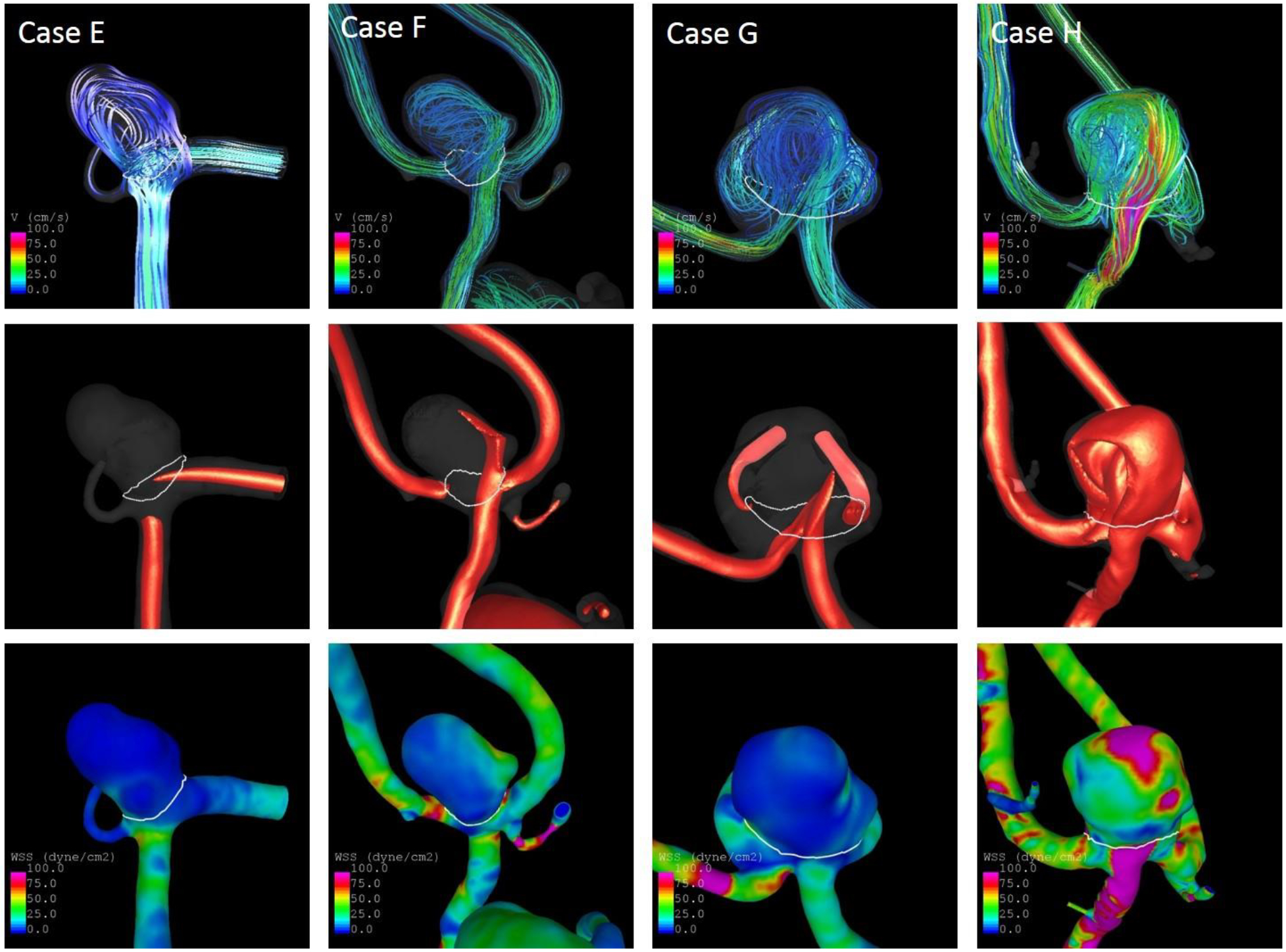
Streamlines (top), inflow jets (middle) and WSS distribution (bottom) at half of the cardiac cycle of the two Japanese aneurysms (e, g) and their similar cases (f, h)

Table 3.

Values of selected variables and predicted probabilities of being ruptured based on the statistical model for the IAs illustrated in Fig. 3.

Case	Population	Asize [cm]	Location	NSI	OSImax	MLN	Pred. Prob	Rupture Status
A	FIN	0.6922	ACOM	0.2443	0.2703	0.3663	0.6609	R
B	US	0.6797	ACOM	0.2405	0.2892	0.3821	0.7329	R
C	FIN	1.6644	ICA-CAV	0.2498	0.4665	0.4504	0.0713	U
D	EUR	1.5896	ICA-CAV	0.2420	0.4845	0.4661	0.0327	U
E	JPN	0.7339	ACOM	0.2168	0.3114	0.3560	0.5550	R
F	US	0.7520	ACOM	0.2218	0.3196	0.3628	0.6142	R
G	JPN	0.8989	ACOM	0.1737	0.3973	0.3256	0.2636	U
H	US	0.8146	ACOM	0.1683	0.4033	0.3435	0.5837	U

ACOM = anterior communicating artery, ICA-CAV = cavernous sinus of the internal carotid artery, Pred. Prob. = predicted probability of being ruptured based on the rupture probability model⁶, rupture status refers to the true rupture status of the aneurysm

Still, overall the definition of rupture status based on similar cases in the data base performed well, especially in the Japanese data. In a clinical setting, it could be used as an illustrational tool – potentially in addition to a statistical model.⁷

Clinical Considerations

For an eventual translation of a statistical model for aneurysm rupture into the clinic, several further steps are needed. First, since the models were mainly developed based on cross-sectional data, they provide the probability of whether the given IA currently is ruptured or unruptured. To assess whether the models could also be used for the assessment of a risk of a future rupture, i.e. whether the underlying assumption that high risk cases resemble those that have already ruptured holds,^5,6,26 they need to be evaluated with more longitudinal data. Second, this study demonstrates how population affects the rupture-probability models of intracranial aneurysms, and thus such models need to be tested in specific populations separately. Third, to be able to apply such a model in a clinical setting, clinicians would need to be provided with a tool for image based IA shape characterization as well as CFD simulations, which seems to be feasible in future.²⁵ Finally, the model could potentially be improved by taking into account additional patient-related information like co-morbidities or social habits including smoking or alcohol consumption.

Conclusion

For development of an aneurysm rupture prediction model based on aneurysm geometry, hemodynamics, and patient characteristics that applies to Japanese and Finnish aneurysms, the inclusion of data from these two cohorts for model training as well as interaction terms between patient population and the other variables in the statistical model is necessary. When including this information, the performance of such a model in Japanese and Finnish data is close to its performance in US or European data. These results suggest that population-specific differences determine how hemodynamics and shape associate with rupture risk in intracranial aneurysms.