Abstract
Apparent diffusion coefficient has limits to differentiate solid tumor from normal tissue or edema in glioblastoma (GBM). This study investigated a microstructure model (MSM) in GBM using a clinically available diffusion imaging technique. The MSM was modified to integrate with bi-polar diffusion gradient waveforms, and applied to 30 patients with newly diagnosed GBM. Diffusion-weighted (DW) images acquired on a 3 T scanner with b-values from 0 to 2500 s/mm2 were fitted in volumes of interest (VOIs) of solid tumor to obtain the apparent restriction size of intracellular water (ARS), the fractional volume of intracellular water (Vin), and extracellular (Dex) water diffusivity. The parameters in solid tumor were compared with those of other tissue types by Students’ t test. For comparison, DW images were fitted by conventional mono-exponential and bi-exponential models. ARS, Dex, and Vin from the MSM in tumor VOIs were significantly greater than those in WM, GM, and edema (P values of .01–.001). ARS values in solid tumors (from 21.6 to 34.5 um) had absolutely no overlap with those in all other tissue types (from 0.9 to 3.5 um). Vin values showed a descending order from solid tumor (from 0.32 to 0.52) to WM, GM, and edema (from 0.05 to 0.25), consisting with the descending cellularity in these tissue types. The parameters from mono-exponential and bi-exponential models could not significantly differentiate solid tumor from all other tissue types, particularly from edema. Further development and histopathological validation of the MSM will warrant its role in clinical management of GBM.
Keywords: Diffusion-weighted imaging, high-order diffusion MR methods, quantitation, glioblastoma
Introduction
Glioblastoma (GBM) is the most common and aggressive primary brain tumor in adults and has poor prognosis with a median survival of ∼14 months despite multimodality therapy with surgery, concurrent chemoradiation therapy, and adjuvant chemotherapy (1, 2) . Postcontrast T1-weighted and fluid-attenuated inversion recovery (FLAIR) T2-weighted magnetic resonance imaging (MRI) images are the primary images to guide treatment and assess tumor progression or therapy response (3). However, the postcontrast T1-weighted MRI identifies blood–brain barrier disruption, which is affected by tumor growth but also by radiation, antiangiogenesis drugs, and chemotherapy. Abnormality on T2 FLAIR images is influenced by T2 changes of tumor cells as well as edema that always coexists within GBM. Limitations of conventional MRI in clinical management of GBM have been recognized and motivate investigations of physiological and metabolic MRI.
Diffusion-weighted (DW) imaging is a technique to measure water molecule mobility in the tissue microscopic environment, and is sensitive to cell density and size, cell membrane permeability, and extracellular space tortuosity. Apparent diffusion coefficient (ADC) quantified from conventional DW images with b-values between 0 and 1000 s/mm2 using a mono-exponential decay is a commonly reported parameter in literature. The correlation between high cellularity and low ADC in tumor animal models and human cancers motivates investigations of roles of ADC in clinical GBM (4-7). One limitation of DW imaging is that coexistence of edema in clinical GBM results in elevated ADC compared with normal white matter (WM) and gray matter (GM). To overcome this challenge, high b-value DW images and high-order diffusion models have been explored in clinical gliomas to differentiate tumor grade and assess therapy response (8-16).
Among the high-order diffusion models, a few models attempt to quantify microstructures in tumors (17, 18). For example, a model, called VERDICT, has been proposed to quantify microstructural properties of colorectal cancer cell lines (19). This model considers cell size, vascular volume fraction and associated pseudodiffusivity, and intracellular and extracellular fractional volumes and diffusivities. Owing to complicity of the VERDICT model, prior knowledge of intracellular and extracellular diffusion coefficients is used to fit in vivo DW images in 2 xenograft animal models. Another model, called temporal diffusion spectroscopy, uses oscillating diffusion gradients to probe cellular structures that restrict intracellular water diffusion by assuming that intracellular water is restricted in impermeable cells (20, 21). Compared with VERDICT, this model simplifies the extracellular water diffusion to a single free diffusion term, and it fits 4 free parameters, including intracellular and extracellular water diffusivities.
Recent studies show that hypercellular tumor volumes (TVs) that can be detected on the DW images with b = 3000 mm2/s in GBM have a prognostic value (22, 23). This technique used a widely available imaging technique and could be easily translated into a clinical trial. A phase II clinical trial targets this hypercellular TV with intensified radiation doses (24).
In this study, we modified the model described in Jiang et al.’s study (25, 26) and applied it to clinical DW images in the patients with GBM. In our clinic, bipolar pulse diffusion gradient waveforms and a high parallel imaging factor were used to reduce eddy current and geometric distortion in the clinical DW images, respectively. We applied the modified model to the DW images with high b-values to investigate whether there were any significant differences in the quantified microstructure parameters between the hypercellular tumors and normal tissue and edema in the patients with GBM. Similar comparisons were made for the conventional ADC and the parameters quantified from the bi-exponential model. This study was the first step to test the possibility of the application of the model quantifying the microstructure parameters using a widely available diffusion technique on the clinical scanner for GBM.
Materials and Methods
Microstructure Model with Bipolar Diffusion Gradients
We assume a DW signal in tissue that can be considered as a sum of water signals from intracellular and extracellular compartments (21):
| [1] |
where is the total magnetization from both water compartments, is the fraction volume of intracellular water, and and are respective diffusion sensitive signals of intracellular and extracellular water. In the previous works of restricted intracellular diffusion (19, 27, 28), a cell has been modeled as an impermeable sphere, which completely restricted diffusion of intracellular water molecules within the spherical space. The analytical formulae of the restricted diffusion signals have been derived for the conventional monopolar diffusion pulse gradient spin echo (PGSE) and oscillating gradient spin echo sequences using the Gaussian phase distribution (GPD) approximation (20, 29-31). It has shown that the GPD approximation of restricted diffusion for the conventional PGSE sequence has sufficient accuracy for most experimental conditions and for sphere and parallel-plane geometry assumptions (32). Therefore, we adopt this formulation to express the restricted diffusion signal of the intracellular water as:
| [2] |
where is the gyromagnetic ratio of proton spin, g(t) is the gradient waveform, Din is the intracellular diffusion coefficient, and and are structure-dependent parameters. The analytical formulae of and for the spherical geometry [provided by a previous work (30)] depend upon the radius (R) of the sphere or cylinder and the nth root of a Bessel function of the first kind. The integral in equation [2] depends upon the specific gradient waveforms g(t) used in the diffusion pulse sequence. On the clinical scanner, the most commonly used gradient waveform is the conventional monopolar PGSE, and the oscillating diffusion gradient wave forms are not available. However, large eddy currents generated in the monopolar diffusion PGSE can produce artifacts on DW images.
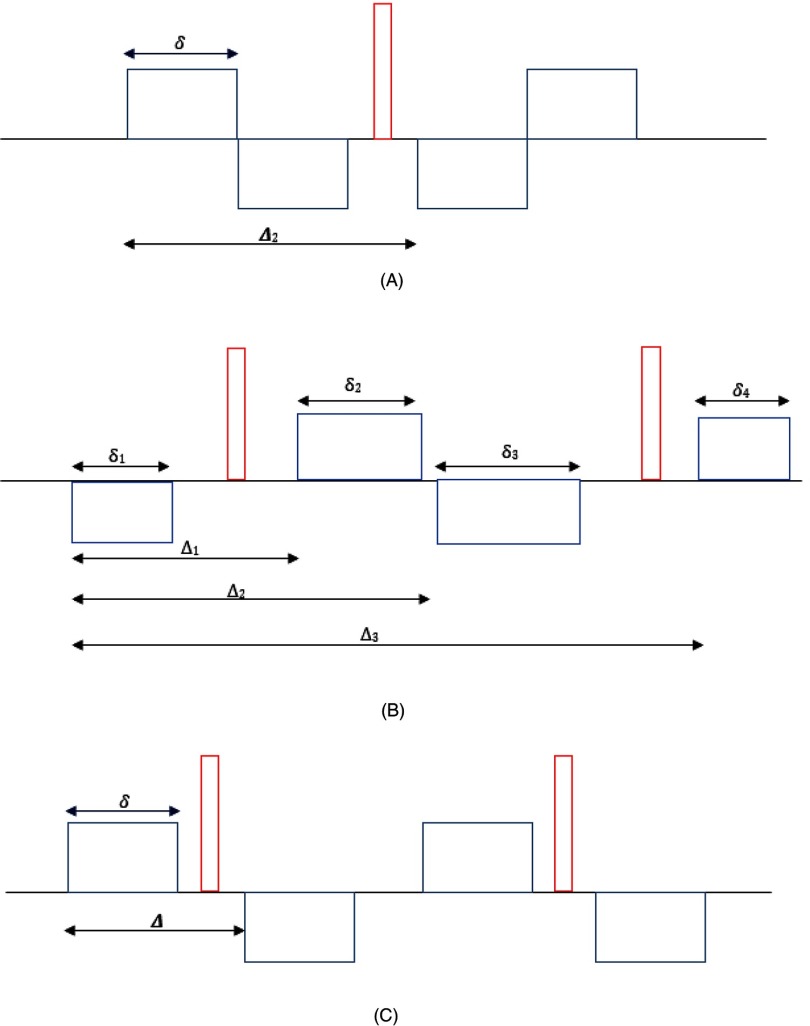
To minimize eddy current–caused artifacts and improve quality of DW images, bipolar diffusion gradient pulse sequences have been introduced on clinical scanners (33). There are a few variations in bipolar diffusion gradient waveforms that have been implemented on the clinical scanners by different vendors. Three common bipolar gradient waveforms, g(t), are illustrated in Figure 1. The first one is introduced by Fordham et al. (34), in which bipolar gradient pulses simply replace the monopolar gradients before and after the 180° radiofrequency (RF) pulse. The second one contains 4 diffusion gradient pulses that are placed before, between, and after 2 180° RF pulses. The 4 diffusion gradient pulse durations and time intervals can be tuned to minimize eddy current effects on DW images, resulting in asymmetric waveforms (Figure 1B). We derived Sin in equation [2] for 3 bipolar diffusion gradient waveforms shown in Figure 1 and provided them in the online supplemental Appendix.
Figure 1.
Schematic plots of 3 bipolar gradient pulse waveforms. Symmetric bipolar diffusion gradients are placed before and after the 180° radiofrequency (RF) pulse (A). Four gradient pulses are placed before, after, and between 2 180° RF pulses (B). Pulse durations and separations can be tuned to minimize eddy currents for a system. Therefore, all 4 gradient pulse durations (δi) and time intervals between the pulses (Δi) can be different. A special case is of b (C). All diffusion gradient pulse durations are the same, and the gradient pulses are placed symmetrically related to the 2 180° RF pulses.
Finally, the extracellular diffusion signal is formulated as follows (20):
| [3] |
where Dex is the extracellular water diffusion, and b is the b-value and depends upon the gradient waveform. For the 3 bipolar diffusion gradient waveforms, b-values are given in equations [A3], [A6], and [A9] in the online supplemental Appendix. Note that 4 free parameters (R, Din, Dex, and Vin) can be estimated by fitting the microstructure model (MSM) to DW images. Here, R can be considered to be an apparent restriction size (ARS) of intracellular water. Also, whether Din was sensitive to the cost function in fitting was investigated.
Bi-Exponential Model
The bi-exponential diffusion model, considered 2 free diffusion components, has been investigated to differentiate tumor from normal tissue and assess tumor response to therapy (35). To compare the parameters estimated by the MSM, we implemented the bi-exponential model:
| [4] |
where S1 and S2 are respective amplitudes of apparent diffusion coefficients of D1 and D2. The fractional volume of water with the small diffusion coefficient is given by:
| [5] |
Again, 4 free parameters (D1, D2, S1, and S2) are fitted from the bi-exponential model.
Conventional Mono-Exponential Model
Conventional ADC is usually fitted to DW images with b = 0 and b = 1000 s/mm2 by a mono-exponential diffusion function as
| [6] |
Patients
Thirty patients (median age, 62 years; males, 19, females, 11) with histologically diagnosed new glioblastoma were included in this study that has been approved by an institutional review board. All patients had MRI scans post surgery but before chemoradiation therapy.
In Vivo MR Imaging
All scans were performed on a 3.0 T scanner (Skyra, Siemens Healthineers, Erlangen, Germany) using a 20-channel head coil. Conventional MR images, 2D T2-FLAIR images, and 3D pre- and postcontrast T1-weighted images using a MPRAGE sequence were acquired. DW images were acquired by a spin-echo echo-planar pulse sequence with diffusion weighting in 3 orthogonal directions and 11 b-values from 0 to 2500 s/mm2 with an incremental step of 250 s/mm2. A bipolar diffusion gradient waveform (shown in Figure 1B) was used to reduce eddy currents and improve quality of DW images. In this sequence, there were 2 180° RF pulses and 4 diffusion gradient pulses. The four diffusion gradient pulses had durations of δ1 = 9.94 milliseconds, δ2 = 15.14 milliseconds, δ3 = 19.8 milliseconds, and δ4 = 5.28 milliseconds. The times intervals between the first and second, the first and third, and the first and fourth gradient pulses were ⊿1 = 20.84 milliseconds, ⊿2 = 36.64 milliseconds, and ⊿3 = 67.34 milliseconds, respectively. Other acquisition parameters included the parallel imaging factor of 4 (GRAPPA) (to reduce echo spacing and hence geometric distortion), TE/TR = 93 / 9300 milliseconds, bandwidth of 1040 Hz/pixel, voxel size of ∼1.3 × 1.3 × 5.2 mm, 30 slices to cover the whole brain, 1 average, and total scan time of 4.50 minutes. It has been shown that diffusion anisotropy is lost or reduced dramatically in T2 FLAIR abnormalities of GBM owing to tumor infiltration and edema (36). To test the loss or reduction of anisotropic diffusion in GBM, DW images were also acquired in 30 directions with b = 1000 s/mm2 and 3 averages. To determine the hypercellular tumor in GBM, a diffusion image volume was acquired at b = 3000 s/mm2 and 4 averages.
Definition of Volumes of Interest
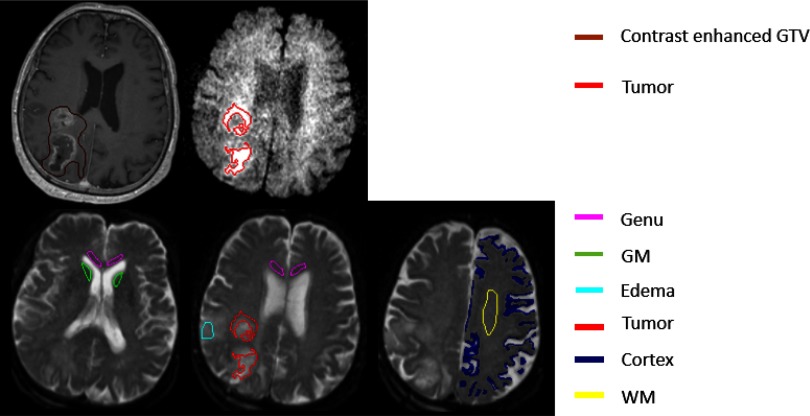
First, we investigated whether microstructure and diffusion parameters in solid components of GBM, estimated by this model, were significantly different from ones in edema regions, normal gray matter (GM), and normal WM. Owing to anticipated low SNRs in DW images, we performed this test in several volumes of interest (VOIs). Previous studies of GBM using advanced imaging have shown that solid tumor components can be beyond the contrast-enhanced gross TVs (22, 37). Also, the T2 abnormality volume can consist of tumor, edema, and a mixture of the 2. However, at high b-values, water signals of edema are attenuated much faster than the hypercellular tumor. Based upon this hypothesis, in previous studies, a TV was created by combining automated thresholding on the DW images with b = 3000 s/mm2, and then these were viewed and edited by a neuroradiologist with more than 10 years of clinical experience (22). The initial TV was created using a threshold of the mean intensity plus 2 standard deviations calculated from a volume of interest in the normal-appearing tissue most contralateral to the T2-abnormality and performed on the DW images with b = 3000 s/mm2. Also, this TV has shown to be significantly correlated with progression-free survival (22). Therefore, we used this TV to characterize microstructure and diffusion parameters by the MSM in this study. Note that this TV is different from the contrast-enhanced TV (Figure 2).
Figure 2.
Illustration of volumes of interest (VOIs) used in the analysis. Brown contours are contrast-enhanced gross tumor volume (GTV) on post-Gd T1-weighted (T1W) images, and red contours are tumor volume (TV) on the diffusion-weighted (DW) images, with b = 3000 s/mm2. Magenta, green, cyan, blue, and yellow contours represent genu, deep gray matter (head of caudate nucleus), edema, cortex, and frontal white matter (WM), respectively.
To compare the behavior of this model in edema to solid tumor in GBM, an edema volume was created within the T2-abnormality but had at least 1 cm away from both the TV used in this study and the contrast-enhanced gross TV. In the cases with tumor recurrence, the edema volume was checked and ensured to have no spatial overlap with the recurrent TV. Also, the VOIs of 2 large WM fiber bundles were drawn: one in the frontal lobe and another in the Genu of corpus callosum. To compare to GM, cortex regions in the frontal and parietal lobes were segmented using the fuzzy c-means algorithm on DW images with b = 0 (T2-weighted images) and ADC maps. To avoid influence of cerebrospinal fluid (CSF), a deep GM structure, the head of caudate nucleus, was carefully chosen. As a total, 6 VOIs were created (Figure 2).
Before fitting the MSM, we investigated fractional anisotropy (FA) of diffusion in the defined hypercellular TV to determine whether we could fit the MSM using mean diffusivities in the TV. The averaged FA was 0.15 ± 0.05 in the TVs, which is consistent with previous reports (36), and 0.41 ± 0.07 in the frontal WM. Therefore, it is reasonable to fit the MSM to the mean diffusion signals in the TV using a sphere assumption and omitting anisotropic diffusion. In the WM, the cylinder-shape assumption was used, while the sphere shape was used in other tissue types.
Before the VOI creation, postcontrast T1-weighted images were reformatted into the axial plane with spatial resolution of 1 × 1 × 3 mm. All other images acquired within the same session were reformatted to the postcontrast T1-weighted images using coordinates in the DICOM header.
Computation of Diffusion Models
Both the MSM and bi-exponential model were implemented using Matlab. The MSM was fitted to the DW images with 11 b-values using a Simplex algorithm in Matlab. We investigated the sensitivity of the objective function to the parameters of R, intracellular diffusion coefficient Din, intracellular volume fraction Vin, and extracellular Dex. If any parameter was not sensitive to the objective function, we would use a fixed value, which would reduce the number of the free parameters and improve the stability of fitting. Simplex was initiated randomly in the ranges of the parameters based on prior knowledge of the physiological parameters given in Table 1. Fitting was run multiple times, and the results were accepted with the minimum mean squared errors (MSE). Similarly, the bi-exponential model was fitted to the same DW images. ADC maps were calculated from DW images with b = 0 and 1000 s/mm2 using in-house Functional Image Analysis Tools (imFIAT).
Table 1.
Ranges of Initial Values of Three Parameters for Microstructure Model Fitting
| Tissue Type | R (μm) | Dex | Vin |
|---|---|---|---|
| Tumor | 5–25 | 1–3 | 0–1 |
| Normal Tissue | 0.5–1.5 | 1–3 | 0–1 |
| Edema | 0.5–1.5 | 1–3 | 0–1 |
Statistical Analysis
To evaluate whether the parameters fitted from the MSM can differentiate tumor from other tissue types, Students’ t test was used and a P-value of 0.05 was considered significant. Similar analysis was applied to the parameters obtained from the bi-exponential model and ADC.
Results
Parameter Characteristics from the MSM
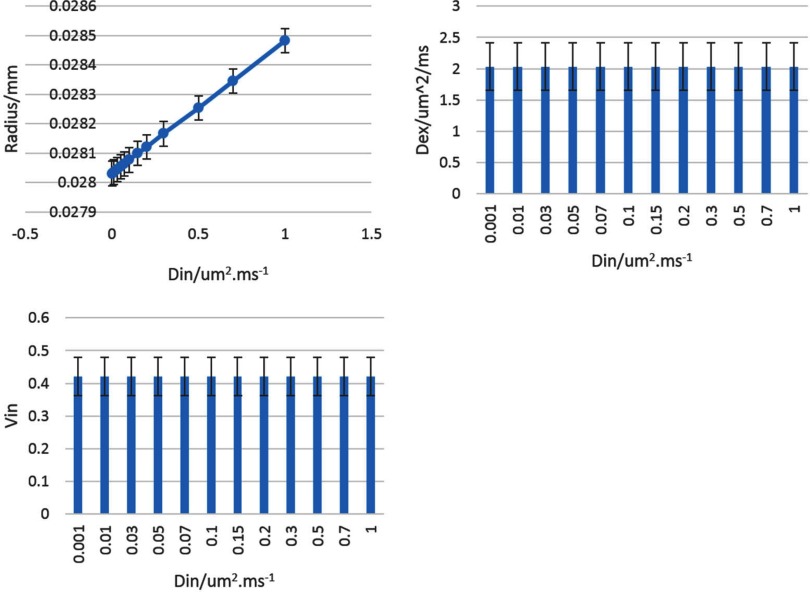
When investigating sensitivity of the objective function to the parameter variation, we found that Din had little sensitivity. To test the influence of Din variations on other parameters, we varied Din from 0.1 to 1.0 μm2/ms. We found that the fitted R in the TVs had no more than 1.5% differences, and Dex and Vin did not show significant differences (Figure 3). Therefore, we fixed Din at 0.1 μm2/ms and varied other 3 parameters in fitting the MSM.
Figure 3.
Changes in R (top left), Dex (top right), and Vin (bottom left) with Din varied from 0.001 to 1 um2ms−1. Error bar is SD.
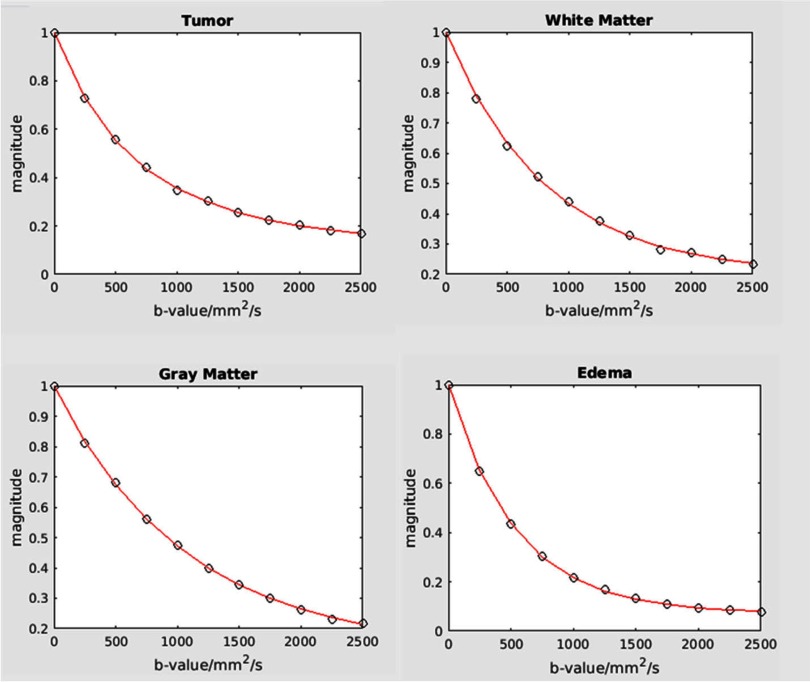
The MSM was fitted to the DW data well in all VOIs, as example curves from TV, WM, GM and edema are shown in Figure 4. Note that the DW signal in the TV was attenuated slower than normal GM and WM at b-values >1000 s/mm2, while the DW signal in edema was attenuated rapidly at low b-values, indicating that a large portion of extracellular water has relative free diffusion.
Figure 4.
Illustration of goodness fit in tumor (top left panel), white matter (top right panel), gray matter (bottom left panel), and edema (bottom right panel). Slide lines: fitted corves; square symbols: data points.
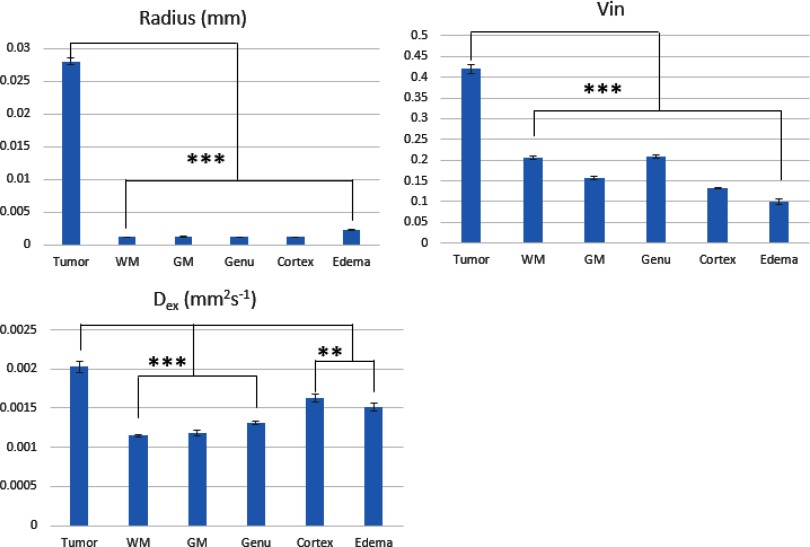
Characteristics of 3 fitted parameters in the TV, normal GM, normal WM, and edema are summarized in Table 2 and Figure 5. Three parameters, R, Dex, and Vin, in the TV were significantly different from normal GM, normal WM, and edema. Specifically, the mean R in the tumor was 28.1 (±0.48) μm and significantly greater than those in other tissue types (range, 1.1–2.3 μm, P < .001). In the latter group, edema had a significant greater R than normal GM and WM (P < .001), which could be because of the existence of a small amount of tumor cells in the edema VOI.
Table 2.
Characteristics of Three Parameters Fitted by the Microstructure Model
|
R (um) (Mean ± SEM) |
Dex/um2/ms (Mean ± SEM) |
Vin (Mean ± SEM) |
|
|---|---|---|---|
| Tumor | 28. 1 ± 0.48 | 2. 03 ± 0.07 | 0.42 ± 0.011 |
| Frontal White Mattera | 1. 20 ± 0.01 | 1. 15 ± 0.01 | 0.21 ± 0.004 |
| Genua | 1. 13 ± 0.01 | 1. 31 ± 0.02 | 0.21 ± 0.005 |
| Deep Gray Matter | 1. 19 ± 0.05 | 1. 19 ± 0.04 | 0.16 ± 0.004 |
| Cortex | 1. 16 ± 0.02 | 1. 62 ± 0.05 | 0.13 ± 0.002 |
| Edema | 2. 32 ± 0.07 | 1. 52 ± 0.05 | 0.10 ± 0.007 |
R was fitted by using a cylinder shape assumption.
Figure 5.
Bar graphs of estimated parameters of R (top left panel), Dex (top right panel), and Vin (bottom left panel) in all tissue types using the microstructure mode. **0.001< P < .01; ***P < .001. Error bar is SEM.
The mean fractional volume of intracellular water, Vin, in the tumor was 0.42 and significantly increased compared with all other tissue types (P < .001). Among normal tissue and edema, as anticipated, Vin had the highest value in the large WM fiber bundles (0.21), intermediate value in the GM regions (0.16–0.13), and the lowest value in edema (0.10) that is consistent with the large amount of extracellular water. Most interestingly, the values of R and Vin in the tumor had absolutely no overlap with the ones in other tissue types, suggesting potential high sensitivity and specificity of R and Vin for differentiating tumor from edema and normal tissue.
The mean Dex in the tumor was 2.03 μm2/ms and significantly greater than that in the normal tissue and in edema (P < .01), which is contributed possibly from edema, micronecrosis, and perfusion mixed in the voxels of GBM. Normal WM and deep GM had Dex values of 1.15–1.31 μm2/ms, which is consistent with other reports (38). Edema had Dex of 1.52 μm2/ms, largely attributing to the great fractional volume of extracellular water. Cortex had Dex of 1.62 μm2/ms, possibly resulting from partial volume average effects with CSF.
Parameter Characteristics from the Bi-Exponential Model
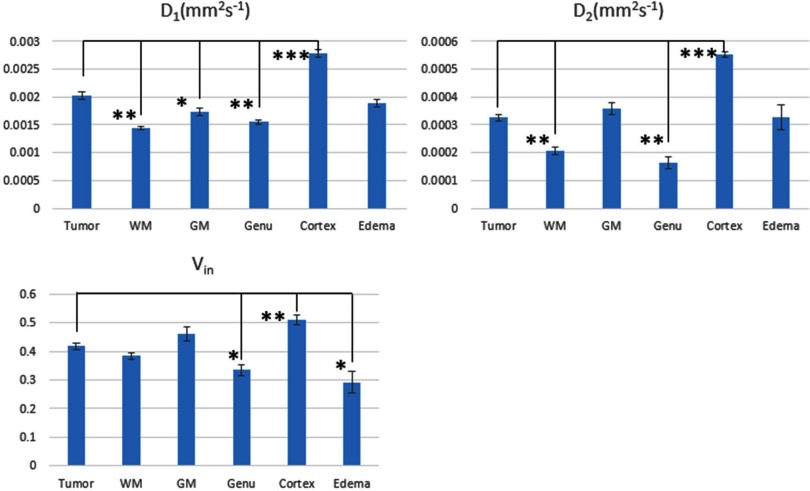
Characteristics of the 3 fitted parameters by the bi-exponential model are summarized in Table 3 and Figure 6. None of the 3 parameters in the tumor significantly and completely differed from the values in all other tissue types. D1 (the large diffusion coefficient) in the tumor was 2.02 ± 0.07 μm2/ms, was not significantly different from edema (1.89 ± 0.06 μm2/ms), but was significantly greater than normal WM and deep GM (P < .05). The cortex had the significantly elevated D1 compared to tumor and other normal tissue (P < .01). D2 in the tumor was 0.34 ± 0.01 μm2/ms, was not significantly different from edema (0.33 ± 0.04 μm2/ms), deep GM, and cortex (0.36 ± 0.02 μm2/ms), but was significantly greater than normal WM (0.16–0.21 μm2/ms, P < .01). Vs in the tumor was 0.42, significantly greater than edema (0.29, P < .05) and genu (0.33, P < .05), and not significantly different from frontal WM and deep GM. Cortex had the highest values in D1, D2, and Vs than tumor and normal WM and GM, possibly owing to the partial volume average with CSF and suggesting that the bi-exponential model is strongly influenced by fluid components.
Table 3.
Characteristics of Three Parameters Fitted by the Bi-Exponential Model
|
D1/um2/ms (Mean ± SEM) |
D2/um2/ms (Mean ± SEM) |
Vs (Mean ± SEM) |
|
|---|---|---|---|
| Tumor | 2. 02 ± 0.07 | 0.34 ± 0.01 | 0.42 ± 0.01 |
| Frontal White Matter | 1. 44 ± 0.03 | 0.21 ± 0.02 | 0.38 ± 0.01 |
| Genu | 1. 55 ± 0.04 | 0.16 ± 0.02 | 0.33 ± 0.02 |
| Deep Gray Matter | 1. 73 ± 0.07 | 0.36 ± 0.02 | 0.46 ± 0.02 |
| Cortex | 2. 78 ± 0.06 | 0.55 ± 0.01 | 0.51 ± 0.02 |
| Edema | 1. 89 ± 0.06 | 0.33 ± 0.04 | 0.29 ± 0.04 |
Figure 6.
Bar graphs of estimated parameters of D1 (top left panel), D2 (top right panel), and Vs (bottom left panel) in all tissue types using the bi-exponential diffusion model. *.01<P < .05; **.001<P < .01; ***P < .001. Error bar is SEM.
To test whether combining all 3 parameters (D1, D2, and Vs) could differentiate tumor from all other tissue types, binary multivariate logistic regression was applied to the data. Backward rejection with P > .1 was used to eliminate the parameters in the logistic regression models. In the first model including the 3 parameters (Table 4), D1 was significant (P < .05), but Vs was not significant, and D2 was marginally significant. However, D2 had a large negative coefficient that could offset the D1 contribution in the model. In the second model where Vs was rejected, D1 was marginally significant, and D2 was not significant. In the final model, D1 was not significant after rejecting D2.
Table 4.
Multivariate Logistic Regression Using the Parameters from the Bi-Exponential Model
| First Model | D1 | D2 | Vs |
|---|---|---|---|
| Coefficient | 1215.93 | −5009.1 | 3.55 |
| P Value | 0.04 | 0.06 | 0.16 |
| Second Model | D1 | D2 | |
| Coefficient | 975.2 | −2327.3 | |
| P Value | 0.075 | 0.19 | |
| Third Model | D1 | ||
| Coefficient | 428.6 | ||
| P Value | 0.23 |
Conventional ADC Model
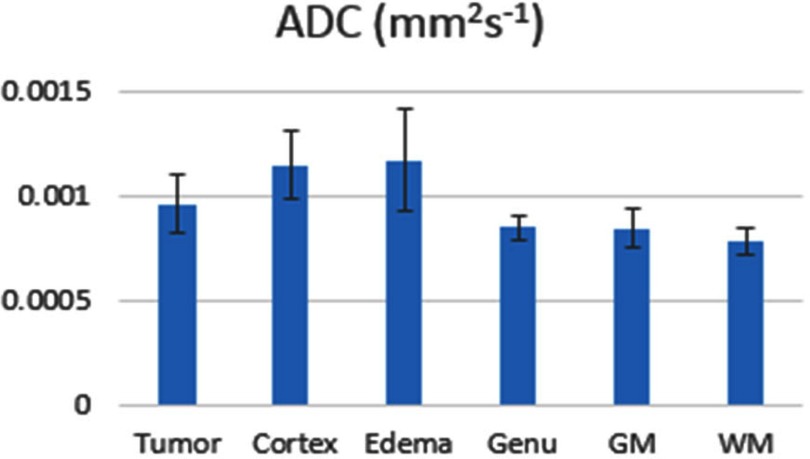
There were no significant differences of ADC between tumor and any other nontumor tissue types (P > .05) (Figure 7). In general, ADC in the tumor was greater than WM and deep GM but lower than edema and cortex, consistent with other reports (7).
Figure 7.
Bar graph of apparent diffusion coefficients in all tissue types using the mono-exponential diffusion model. Error bar is SEM.
Discussion
In this study, we modified the model of (20, 25, 26, 29-31) to fit the DW images acquired with a widely available bipolar pulse diffusion gradient imaging and characterize microstructure and diffusion properties of the hypercellular tumor in patients with GBM. We found that 3 parameters (Vin, R, and Dex) in the tumor were substantially and significantly different from edema and normal tissue. The bi-exponential diffusion model that does not explicitly model the restricted diffusion of intracellular water could not robustly differentiate GBM from edema and normal brain tissue. ADC that ignores intravoxel heterogeneous diffusion in brain tissue and tumor failed to differentiate GBM from edema and normal tissue. The microstructure model has a great promise to aid in to conventional MRI for GBM diagnosis, image-guide therapy, and response assessment. Further validation with histopathology will warrant the role of the microstructure mode in the clinical management of GBM.
In the current study, the fractional volume of intracellular water, Vin,, in GBM estimated by the microstructure model was found substantially different from edema and normal tissue. The Vin in the TV had the largest value, which makes possible to differentiate the GBM from surrounding tissue. Also, GBM has enlarged cell size and nucleus, and increased cell density, which can increase Vin measured in image voxels, and has micronecrosis and edema, which can reduce Vin (39, 40). In the current study, the estimated Vin in GBM by the microstructure model was 1.75-fold greater than that reported in a previous study that included primary and metastatic cancers and used the bi-exponential diffusion model (27). Historically, the bi-exponential diffusion model often results in an underestimated Vin, for which several possible causes have been discussed (38). The underestimation in Vin can be caused by the transcytolemmal water exchange that is omitted in the model as well as low SNR in DW images (41). Also, T2 differences between intracellular and extracellular water could affect the estimated Vin values, which will be discussed further in the last paragraph. Diffusion gradient, b-value range, diffusion model, and subject age all have an influence on the estimated Vin (4). As expected, the lowest Vin value was found in edema, consistent with the notion of a large amount of extracellular water in the region. The Vin values in 2 large WM fiber bundles and GM are between the solid GBM and edema, suggesting that the MSM has the potential to differentiate GBM from surrounding tissue. In this study, we evaluated anisotropic diffusion in the hypercellular TV and found low FA (0.15 as a mean value). Therefore, we did not consider anisotropic diffusion in the MSM. In the future study, anisotropic diffusion could be considered in the microstructure model.
Our microstructure model yielded the substantial greater R in GBM than in normal GM, normal WM, and edema. R could be considered as the apparent restriction size of intracellular water and a possible biomarker to differentiate GBM from normal tissue. The R value should be considered as an average value over a distribution. Previous studies have shown the increased radius of tumor cells compared with that of normal tissue using the microstructure model or VERDICT model, and the reasonable correlation between the DW image–estimated cellularity and histopathologically determined cellularity (19, 21). A pathological study in GBM shows that the radius of GBM cells can be as large as 20 um with a mean of 10 μm and a standard deviation of 11 μm (42). The size of the apparent restriction space estimated in our model is larger than the reported cell size. Many factors can cause an overestimation in the restriction size of intracellular water in GBM. It is most likely that the highly permeable cell membrane cannot restrict intracellular water diffusion like a hard boundary. Therefore, the soft boundary increases the estimated radius so that we could call the estimated radius from our MSM as an effective radius. The low SNR in DW images could further cause an overestimate of R (43). Owing to the diffuse nature of GBM, diffused tumor cells can be found in the edema region (44, 45), which could be the cause of the slight but significant increase in the apparent restriction size in the edema region. Further studies could be carried out to investigate whether combining R and Vin in the image voxels with edema can provide information on the GBM cell infiltration and distribution.
In the current study, the value of Dex in GBM by the microstructure model was found significantly greater than those in normal GM, normal WM and edema, which is similar to one by the bi-exponential diffusion model (Table 3), and also consistent with the values reported by Mulkern et al. (38). Dex in GBM is affected by the large quantity of extracellular water owing to coexistence of edema, and to a small extent by micronecrosis and perfusion (40). To reduce the number of free parameters in the model, we did not account for the perfusion-caused pseudo diffusion in Dex. However, we have tested the perfusion effect on Dex in the TV VOIs in 30 patients using the approach in (46). We estimated that the pseudo diffusion coefficient was ∼0.15 um2/ms, which was 13.5 times smaller than Dex (2.03 um2/ms) in the tumor VOIs. Thus, in the TV VOIs defined in our study, omitting the perfusion effect did not cause a substantial overestimate in Dex. Note that the TV VOI used in our study is not the contrast-enhanced TV. We believe that the high Dex in GBM could mainly be due to edema. The relative high values of Dex in cortex and edema are likely because of the partial volume average of CSF in the cortex VOI and the large amount of extracellular water in the edema region, respectively.
As discussed in Introduction, modeling microstructure and diffusion properties in tumors has been attempted by different models (17, 18, 20, 21, 28). In general, these models fit more free parameters and require long acquisition times. The signal-to-noise ratio (SNR) of DW images is also a limiting factor to produce robust fitted parameters. Furthermore, there are great time restriction, technology availability, and other practical considerations when acquiring DW images in the patients with GBM on a clinical scanner. For example, we used a bipolar pulse diffusion gradient waveform to reduce eddy current–induced artifacts and a high parallel imaging factor to improve geometrics accuracy. With these acquisition limitations, we modified and tested the model in the literature (18) and (19) using the widely available technology on a clinical scanner in the patients with GBM. For other bipolar diffusion gradient waveforms, we provided equations of the model in the online supplemental Appendix.
The MSM showed the prognostic potential and also the opportunity to better distinguish GBM from normal tissue and edema. However, the current study has a few limitations. First, our sample size was not large, with only 30 patients. This could result in overfitting. The MSM needs to be further validated in an independent large cohort of patients in future. Second, the restriction space of intracellular water is modeled as an impermeable sphere, which has been used in both VERDICT and temporal diffusion spectroscopy model (19, 21, 28). A previous simulation work suggests that omitting water exchange at the boundary of the restriction space of water diffusion leads to an underestimation of Vin but has little influence on the estimation of the space size (43). Whether omitting the permeability of cell membrane or restriction space could lead to an overestimation or underestimation of the size of the restriction space in GBM needs further investigation. Anisotropic diffusion was not considered in this study, which could be considered in the future work, particularly for the regions with tumor cell infiltration. Nevertheless, the microstructure model using a clinically available diffusion pulse sequence leads to better differentiation between the hypercellular tumor and normal tissue or edema than the bi-exponential and mono-exponential models.
Conclusion
The MSM considers the restricted diffusion of intracellular water, and differentiates hypercellular tumor of GBM from normal tissue and edema better than free diffusion-based mono-exponential and bi-exponential models. Some parameters from the MSM also reveal the similarity in normal tissue. Further development and histopathological validation of the MSM will warrant its role in clinical management of GBM.
Supplemental Materials
Acknowledgment
This work was in part supported by NIH/NCI grant UO1 CA183848. We would like to thank Dr. Himanshu Bhat from Siemens Healthineers for providing information on diffusion gradient pulses.
Conflicts of Interest: There are no conflicts of interest to declare.
Footnotes
- ADC
- apparent diffusion coefficient
- ARS
- apparent restriction size of intracellular water
- R
- cell radius
- CSF
- cerebrospinal fluid
- Sin
- diffusion sensitive signals of intracellular water
- Sex
- diffusion sensitive signals of extracellular water
- DW
- diffusion-weighted
- Dex
- extracellular diffusion coefficient
- Vin
- fractional volume of intracellular water
- Vs
- fractional volume of water with the small diffusion coefficient
- GPD
- Gaussian Phase Distribution
- GBM
- glioblastoma
- Din
- intracellular diffusion coefficient
- MSM
- microstructure model
- MSE
- mean squared errors
- PGSE
- pulse gradient spin echo
- SNR
- signal-to-noise ratio
- TV
- tumor volume
- VOIs
- volumes of interest
- WM
- white matter
Reference
- 1.Stupp R, Mason WP, van den Bent MJ, Weller M, Fisher B, Taphoorn MJB, Belanger K, Brandes AA, Marosi C, Bogdahn U, Curschmann J, Janzer RC, Ludwin SK, Gorlia T, Allgeier A, Lacombe D, Cairncross JG, Eisenhauer E, Mirimanoff RO. Radiotherapy plus concomitant and adjuvant temozolomide for glioblastoma. N Engl J Med. 2005;352:987–996. [DOI] [PubMed] [Google Scholar]
- 2.Prados MD, Chang SM, Butowski N, DeBoer R, Parvataneni R, Carliner H, Kabuubi P, Ayers-Ringler J, Rabbitt J, Page M, Fedoroff A, Sneed PK, Berger MS, McDermott MW, Parsa AT, Vandenberg S, James CD, Lamborn KR, Stokoe D, Haas-Kogan DA. Phase II study of erlotinib plus temozolomide during and after radiation therapy in patients with newly diagnosed glioblastoma multiforme or gliosarcoma. J Clin Oncol. 2009;27:579–584. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Wen PY, Macdonald DR, Reardon DA, Cloughesy TF, Sorensen AG, Galanis E, DeGroot J, Wick W, Gilbert MR, Lassman AB, Tsien C, Mikkelsen T, Wong ET, Chamberlain MC, Stupp R, Lamborn KR, Vogelbaum MA, van den Bent MJ, Chang SM. Updated response assessment criteria for high-grade gliomas: response assessment in neuro-oncology working group. J Clin Oncol. 2010;28:1963–1972. [DOI] [PubMed] [Google Scholar]
- 4.Sugahara T, Korogi Y, Kochi M, Ikushima I, Shigematu Y, Hirai T, Okuda T, Liang L, Ge Y, Komohara Y, Ushio Y, Takahashi M. Usefulness of diffusion-weighted MRI with echo-planar technique in the evaluation of cellularity in gliomas. J Magn Reson Imaging. 1999;9:53–60. [DOI] [PubMed] [Google Scholar]
- 5.Chenevert TL, Stegman LD, Taylor JM, Robertson PL, Greenberg HS, Rehemtulla A, Ross BD. Diffusion magnetic resonance imaging: an early surrogate marker of therapeutic efficacy in brain tumors. J Natl Cancer Inst. 2000;92:2029–2036. [DOI] [PubMed] [Google Scholar]
- 6.Lyng H, Haraldseth O, Rofstad EK. Measurement of cell density and necrotic fraction in human melanoma xenografts by diffusion weighted magnetic resonance imaging. Magn Reson Med. 2000;43:828–836. [DOI] [PubMed] [Google Scholar]
- 7.Guo AC, Cummings TJ, Dash RC, Provenzale JM. Lymphomas and high-grade astrocytomas: comparison of water diffusibility and histologic characteristics. Radiology. 2002;224:177–183. [DOI] [PubMed] [Google Scholar]
- 8.Sui Y, Wang H, Liu G, Damen FW, Wanamaker C, Li Y, Zhou XJ. Differentiation of low- and high-grade pediatric brain tumors with high b-value diffusion-weighted MR imaging and a fractional order calculus model. Radiology. 2015;277:489–496. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Niendorf T, Dijkhuizen RM, Norris DG, van Lookeren Campagne M, Nicolay K. Biexponential diffusion attenuation in various states of brain tissue: implications for diffusion-weighted imaging. Magn Reson Med. 1996;36:847–857. [DOI] [PubMed] [Google Scholar]
- 10.Maier SE, Bogner P, Bajzik G, Mamata H, Mamata Y, Repa I, Jolesz FA, Mulkern RV. Normal brain and brain tumor: multicomponent apparent diffusion coefficient line scan imaging. Radiology. 2001;219:842–849.Epub 2001/05/29. [DOI] [PubMed] [Google Scholar]
- 11.Kwee TC, Galbán CJ, Tsien C, Junck L, Sundgren PC, Ivancevic MK, Johnson TD, Meyer CR, Rehemtulla A, Ross BD, Chenevert TL. Intravoxel water diffusion heterogeneity imaging of human high-grade gliomas. NMR Biomed. 2009;23:179–187. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Raab P, Hattingen E, Franz K, Zanella FE, Lanfermann H. Cerebral gliomas: diffusional kurtosis imaging analysis of microstructural differences. Radiology. 2010;254:876–881. [DOI] [PubMed] [Google Scholar]
- 13.Van Cauter S, Veraart J, Sijbers J, Peeters RR, Himmelreich U, De Keyzer F, Van Gool SW, Van Calenbergh F, De Vleeschouwer S, Van Hecke W, Sunaert S. Gliomas: diffusion kurtosis MR imaging in grading. Radiology. 2012;263:492–501. [DOI] [PubMed] [Google Scholar]
- 14.Mardor Y, Pfeffer R, Spiegelmann R, Roth Y, Maier SE, Nissim O, Berger R, Glicksman A, Baram J, Orenstein A, Cohen JS, Tichler T. Early detection of response to radiation therapy in patients with brain malignancies using conventional and high b-value diffusion-weighted magnetic resonance imaging. JCO. 2003;21:1094–1100. [DOI] [PubMed] [Google Scholar]
- 15.Szczepankiewicz F, van Westen D, Englund E, Westin C-F, Ståhlberg F, Lätt J, Sundgren PC, Nilsson M. The link between diffusion MRI and tumor heterogeneity: mapping cell eccentricity and density by diffusional variance decomposition (DIVIDE). Neuroimage. 2016;142:522–532. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.White NS, McDonald CR, Farid N, Kuperman JM, Kesari S, Dale AM. Improved conspicuity and delineation of high-grade primary and metastatic brain tumors using “restriction spectrum imaging”: quantitative comparison with high b-value DWI and ADC. AJNR Am J Neuroradiol. 2013;34:958–964. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Lemberskiy G, Fieremans E, Veraart J, Deng F-M, Rosenkrantz AB, Novikov DS. Characterization of prostate microstructure using water diffusion and NMR relaxation. 2018;6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Reynaud O, Winters KV, Hoang DM, Wadghiri YZ, Novikov DS, Kim SG. Pulsed and oscillating gradient MRI for assessment of cell size and extracellular space (POMACE) in mouse gliomas. NMR Biomed. 2016;29:1350–1363. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Panagiotaki E, Walker-Samuel S, Siow B, Johnson SP, Rajkumar V, Pedley RB, Lythgoe MF, Alexander DC. Noninvasive quantification of solid tumor microstructure using VERDICT MRI. Cancer Res. 2014;74:1902–1912. [DOI] [PubMed] [Google Scholar]
- 20.Xu J, Does MD, Gore JC. Quantitative characterization of tissue microstructure with temporal diffusion spectroscopy. J Magn Reson. 2009;200:189–197. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Tian X, Li H, Jiang X, Xie J, Gore JC, Xu J. Evaluation and comparison of diffusion MR methods for measuring apparent transcytolemmal water exchange rate constant. J Magn Reson. 2017;275:29–37. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Pramanik PP, Parmar HA, Mammoser AG, Junck LR, Kim MM, Tsien CI, Lawrence TS, Cao Y. Hypercellularity components of glioblastoma identified by high b-value diffusion-weighted imaging. Int J Radiat Oncol Biol Phys. 2015;92:811–819. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Wahl DR, Kim MM, Aryal MP, Hartman H, Lawrence TS, Schipper MJ, Parmar HA, Cao Y. Combining perfusion and high b-value diffusion MRI to inform prognosis and predict failure patterns in glioblastoma. Int J Radiat Oncol Biol Phys. 2018;102:757–764. [DOI] [PubMed] [Google Scholar]
- 24.Kim MM, Parmar HA, Aryal MP, Mayo CS, Balter JM, Lawrence TS, Cao Y. Developing a pipeline for multiparametric MRI-guided radiation therapy: initial results from a Phase II clinical trial in newly diagnosed glioblastoma. Tomography. 2019;5:118–126. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Jiang X, Li H, Xie J, McKinley ET, Zhao P, Gore JC, Xu J. In vivo imaging of cancer cell size and cellularity using temporal diffusion spectroscopy. Magn Reson Med. 2017;78:156–164. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Jiang X, Li H, Xie J, Zhao P, Gore JC, Xu J. Quantification of cell size using temporal diffusion spectroscopy. Magn Reson Med. 2016;75:1076–1085. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Jiang X, Li H, Zhao P, Xie J, Khabele D, Xu J, Gore JC. Early detection of treatment-induced mitotic arrest using temporal diffusion magnetic resonance spectroscopy. Neoplasia. 2016;18:387–397. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Li K, Li H, Zhang X-Y, Stokes AM, Jiang X, Kang H, Quarles CC, Zu Z, Gochberg DF, Gore JC, Xu J. Influence of water compartmentation and heterogeneous relaxation on quantitative magnetization transfer imaging in rodent brain tumors. Magn Reson Med. 2016;76:635–644. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Neuman CH. Spin echo of spins diffusing in a bounded medium. J Chem Phys. 1974;60:4508–4511. [Google Scholar]
- 30.Stepisnik J. Time-dependent self-diffusion by NMR spin echo. Physica B. 1993;183:343–350. [Google Scholar]
- 31.Callaghan PT. Pulsed-gradient spin-echo NMR for planar, cylindrical and spherical pores under conditions of wall relaxation. J Magn Reson. 1995;113:53–59. [Google Scholar]
- 32.Balinov B, Jonsson B, Linse P, Soderman O. The NMR self-diffusion method applied to restricted diffusion - simulation of echo attenuation from molecules in spheres and between planes. J Magn Reson A. 1993;104:17. [Google Scholar]
- 33.Reese TG, Heid O, Weisskoff RM, Wedeen VJ. Reduction of eddy-current-induced distortion in diffusion MRI using a twice-refocused spin echo. Magn Reson Med. 2003;49:177–182. [DOI] [PubMed] [Google Scholar]
- 34.Fordham EJ, Hall LD, Ramakrishnan TS, Sharpe MR, Hall C. Saturation gradients in drainage of porous-media - NMR imaging measurements. AiChE J. 1993;39:1431–1443. [Google Scholar]
- 35.Issa B. In vivo measurement of the apparent diffusion coefficient in normal and malignant prostatic tissues using echo-planar imaging. J Magn Reson Imaging. 2002;16:196–200. [DOI] [PubMed] [Google Scholar]
- 36.Field AS, Alexander AL. Diffusion tensor imaging in cerebral tumor diagnosis and therapy. Top Magn Reson Imaging. 2004;15:315–324. [DOI] [PubMed] [Google Scholar]
- 37.Law M, Young RJ, Babb JS, Peccerelli N, Chheang S, Gruber ML, Miller DC, Golfinos JG, Zagzag D, Johnson G. Gliomas: predicting time to progression or survival with cerebral blood volume measurements at dynamic susceptibility-weighted contrast-enhanced perfusion MR imaging. Radiology. 2008;247:490–498. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Mulkern RV, Gudbjartsson H, Westin C-F, Zengingonul HP, Gartner W, Guttmann CRG, Robertson RL, Kyriakos W, Schwartz R, Holtzman D, Jolesz FA, Maier SE. Multi-component apparent diffusion coefficients in human brain. NMR Biomed. 1999;12:51–62. [DOI] [PubMed] [Google Scholar]
- 39.Nafe R, Franz K, Schlote W, Schneider B. Morphology of tumor cell nuclei is significantly related with survival time of patients with glioblastomas. Clin Cancer Res. 2005;11:2141–2148. [DOI] [PubMed] [Google Scholar]
- 40.LaViolette PS, Mickevicius NJ, Cochran EJ, Rand SD, Connelly J, Bovi JA, Malkin MG, Mueller WM, Schmainda KM. Precise ex vivo histological validation of heightened cellularity and diffusion-restricted necrosis in regions of dark apparent diffusion coefficient in 7 cases of high-grade glioma. Neuro Oncol. 2014;16:1599–1606. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Dietrich O, Raya JG, Reeder SB, Reiser MF, Schoenberg SO. Measurement of signal-to-noise ratios in MR images: influence of multichannel coils, parallel imaging, and reconstruction filters. J Magn Reson Imaging. 2007;26:375–385. [DOI] [PubMed] [Google Scholar]
- 42.Eidel O, Neumann J-O, Burth S, Kieslich PJ, Jungk C, Sahm F, Kickingereder P, Kiening K, Unterberg A, Wick W, Schlemmer H-P, Bendszus M, Radbruch A. Automatic analysis of cellularity in glioblastoma and correlation with ADC using trajectory analysis and automatic nuclei counting. PLoS One. 2016;11:11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Li H, Jiang X, Xie J, Gore JC, Xu J. Impact of transcytolemmal water exchange on estimates of tissue microstructural properties derived from diffusion MRI. Magn Reson Med. 2017;77:2239–2249. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Kelly PJ, Daumas-Duport C, Kispert DB, Kall BA, Scheithauer BW, Illig JJ. Imaging-based stereotaxic serial biopsies in untreated intracranial glial neoplasms. J Neurosurg. 1987;66:865–874. [DOI] [PubMed] [Google Scholar]
- 45.Chang EL, Akyurek S, Avalos T, Rebueno N, Spicer C, Garcia J, Famiglietti R, Allen PK, Chao KSC, Mahajan A, Woo SY, Maor MH. Evaluation of peritumoral edema in the delineation of radiotherapy clinical target volumes for glioblastoma. Int J Radiat Oncol Biol Phys. 2007;68:144–150. [DOI] [PubMed] [Google Scholar]
- 46.Lebihan D, Breton E, Lallemand D, Aubin ML, Vignaud J, Lavaljeantet M. Separation of diffusion and perfusion in intravoxel incoherent motion MR imaging. Radiology. 1988;168:497–505. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.