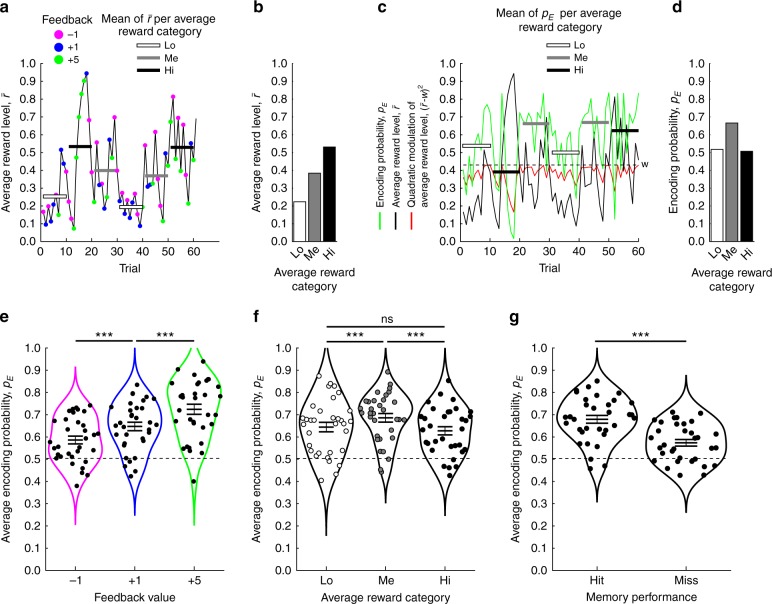
Fig. 2. Computational model.

a–d illustrates how parameter values in the computational model derive from the behavioral data, here for one representative participant. a The average reward level ($\overline{r}$, black line) tracks preceding feedback values as an exponential running average. The average $\overline{r}$ of ten trials within the different average reward categories (Hi, Me, and Lo) are respectively indicated by white, gray, and black bars. b. The average $\overline{r}$ across average reward categories in (a). c When the encoding probability (p_E, green line) is nonlinearly (inverted U-shape) modulated by average reward levels ($\overline{r}$, black line), p_E increases when $\overline{r}$ approaches the optimal level of average reward (w, dashed line). By contrast, p_E decreases whenever $\overline{r}$ becomes larger or smaller than w. To further illustrate the nonlinear contribution of $\overline{r}$ to p_E, the quadratic term ${\left(\overline{r}-w\right)}^2$ is displayed as a red line. White, gray, and black bars respectively illustrate the average p_E of the ten trials within each average reward category. d The average p_E across the average reward categories in (c). e Across participants, the most parsimonious model indicates that the encoding probability p_E increases monotonically as a function of feedback value, but is nonlinearly modulated by average reward (f). g On average the model predicts higher encoding probabilities for subsequent hits as compared with misses. ***p < 0.001, ns not significant (i.e., p > 0.05), indicates the p value for paired t-test. The horizontal lines in e, f, and g indicate mean ± SEM. Source data are provided as a Source Data file.