Fig. 2. Machine learning inverse design of an arbitrary 3D vectorial field using the MANN.
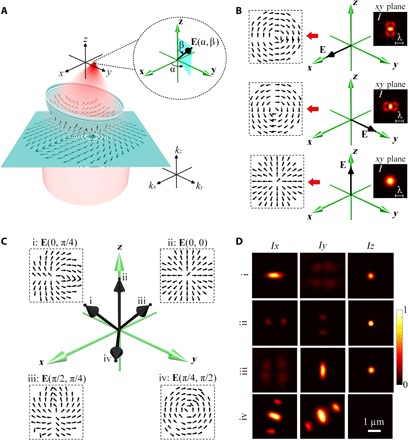
(A) Schematic illustration of how a 2D vector field in the hologram plane is transformed to a 3D vectorial field in the image plane through a vectorially weighted Ewald sphere. Inset shows the definition of a 3D vectorial field in a spherical coordinate system. (B) The azimuthal spatial components modulated by a π-phase step with an orientation along the horizontal and vertical directions are used to independently manipulate the transverse electric field components Ex and Ey, respectively. A radial spatial component is used for the manipulation of the longitudinal electric field component Ez. The insets show the corresponding intensity distributions of these azimuthal and radial spatial components in the image plane. (C) Schematic of the four 3D vectorial fields derived from the MANN. The insets represent the MANN-derived 2D vector field distributions. (D) Experimental characterization of the three electric field components (Ex, Ey, Ez) of 3D vectorial fields through two-photon fluorescence imaging of the gold nanorods with an orientation along x, y, and z directions, respectively.
