Fibration symmetries uncover the building blocks of biological networks

Significance

The success of symmetries in explaining the physical world, from general relativity to the standard model of particle physics and all phases of matter, raises the question of why the same concept could not be equally applied to explain emergent properties of biological systems. In other words, we ask—if life is an emergent property of physics—why the same symmetry principles that explain physics could not explain the organizing principle of life. Here we show that a particular form of symmetry, called symmetry fibration, explains the building blocks of biological networks and other social and infrastructure networks. This result opens the way to understand how information-processing networks are assembled from the bottom up.

Abstract

A major ambition of systems science is to uncover the building blocks of any biological network to decipher how cellular function emerges from their interactions. Here, we introduce a graph representation of the information flow in these networks as a set of input trees, one for each node, which contains all pathways along which information can be transmitted in the network. In this representation, we find remarkable symmetries in the input trees that deconstruct the network into functional building blocks called fibers. Nodes in a fiber have isomorphic input trees and thus process equivalent dynamics and synchronize their activity. Each fiber can then be collapsed into a single representative base node through an information-preserving transformation called “symmetry fibration,” introduced by Grothendieck in the context of algebraic geometry. We exemplify the symmetry fibrations in gene regulatory networks and then show that they universally apply across species and domains from biology to social and infrastructure networks. The building blocks are classified into topological classes of input trees characterized by integer branching ratios and fractal golden ratios of Fibonacci sequences representing cycles of information. Thus, symmetry fibrations describe how complex networks are built from the bottom up to process information through the synchronization of their constitutive building blocks.

A central theme in systems science is to break down the system into its fundamental building blocks to then uncover the principles by which complex collective behavior emerges from their interactions (1–3). In number theory, every natural number can be represented by a unique product of primes. Thus, prime numbers are the building blocks of natural numbers. This mathematical notion of building blocks is extended to the more abstract notion of group theory since finite groups can also be factored into simple subgroups (4). The latter example, entirely abstract as it may be, has important implications for natural systems due to the fundamental relationship between group theory and the notion of symmetry that has led to the discovery of the fundamental building blocks of matter, such as quarks and leptons (3, 5). Here we ask whether similar principles of symmetry can uncover the fundamental building blocks of biological networks (1, 2, 6, 7). Primary examples of these networks are gene regulatory networks that control gene expression in cells (2, 8–10); as well as metabolic networks, cellular processes and pathways, neural networks, and ecosystems; and, beyond biology, other information-processing networks like social and infrastructure networks (7). Previous studies have identified building blocks or “network motifs” (2, 6, 8) by looking for patterns in the network that appear more often than they would by pure chance. The crux of the matter is to test whether the building blocks of these networks obey a predictive principle that explains how the cell functions and whether such a principle can be expressed in the language of symmetries.

We introduce the use of symmetries in biological networks by analyzing the transcriptional regulatory network of bacterium Escherichia coli (11), since this is a well-characterized network. We find that this network exhibits fibration symmetries (12–14), first introduced by Grothendieck (12) in the context of algebraic geometry.

Symmetry fibrations are morphisms between networks that identify clusters of synchronized genes (called fibers) with isomorphic input trees. Genes in a fiber are collapsed by a symmetry fibration into a single representative gene called the base. The fibers are then the synchronized building blocks of the genetic network and symmetry fibrations are transformations that preserve the dynamics of information flow in the network. We use this symmetry principle to classify the building blocks into topological classes of input trees characterized by integer branching ratios and complex topologies with golden ratios of Fibonacci sequences representing cycles in the network. We then show that symmetry fibrations explain synchronization patterns of gene coexpression in cells and universally apply to a range of complex networks across different species and domains beyond biology.

Results

We search for symmetries in the E. coli transcriptional regulatory network [most updated compilation at RegulonDB (11)] where nodes are genes and a directed link represents a transcriptional regulation (SI Appendix, section III).

A directed link from a source gene $i$ to a target gene $j$ in a transcriptional regulatory network represents a direct interaction where gene $i$ encodes for a transcription factor that binds to the binding site of gene $j$ to regulate (activate or repress) its expression. Such a link represents a regulatory “message” sent by the source to the target gene using the transcription factor as a “messenger.” This process defines the “information flow” in the system which is not restricted to two interacting genes, but it is transferred to different regions within the network that are accessible through the connecting pathways. The information arriving to a gene contains the entire history transmitted through all pathways that reach this gene. We formalize this process of communication between genes with the notion of “input tree” of the gene. In a network $G=\left(N_G,E_G\right)$ with $N_G$ nodes and $E_G$ directed edges, for every gene $i\in N_G$ there is a corresponding input tree, denoted as $T_i$, which is the tree of all pathways of $G$ ending at $i$. More precisely, $T_i$ is a rooted tree with a selected node $i$ at the root, such that every other node $j$ in the tree represents the initial node of a path in the network ending at $i$.

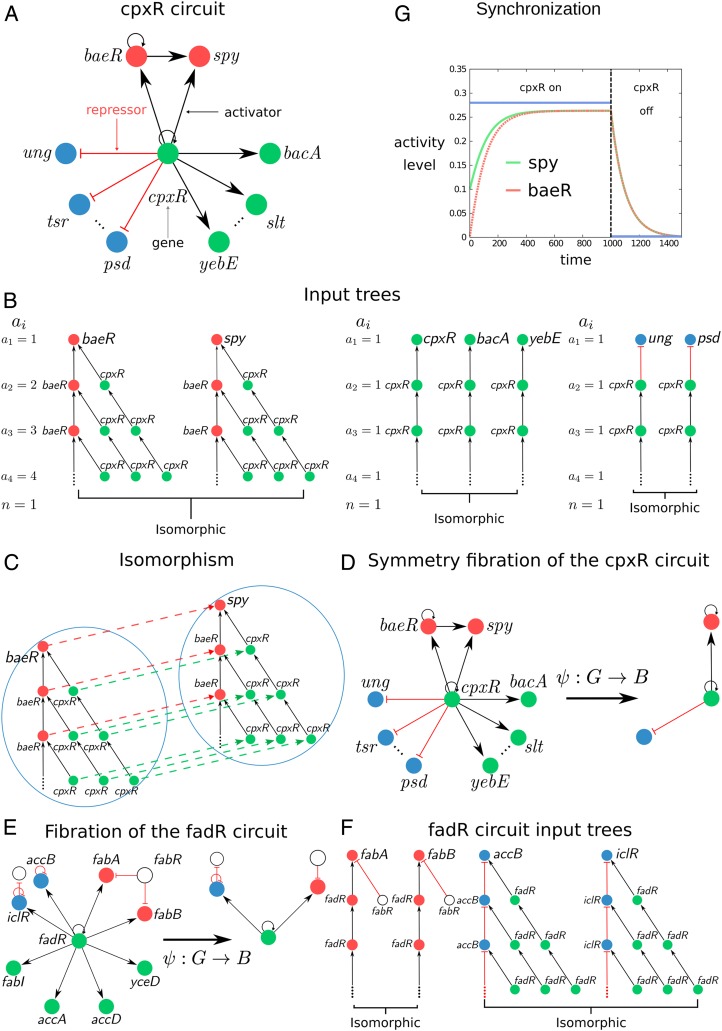
Next, we analyze the input trees in the E. coli subcircuit shown in Fig. 1A regulated by gene cpxR which regulates its own expression (via an autoregulation activator loop) and also regulates other genes as shown in Fig. 1A. Gene cpxR is not regulated by any other transcription factor in the network, so we say that this gene forms its own “strongly connected component”; see below. Therefore, it is an ideal simple circuit to explain the concept of fibration.

Fig. 1.

Definition of input tree, symmetry fibration, fiber, and base. (A) The circuit controlled by the cpxR gene regulates a series of fibers as shown by the different-colored genes. The circuit regulates more genes represented by the dotted lines which are not displayed for simplicity. The full lists of genes and operons in this circuit are in SI Appendix, Table VI, ID nos. 27, 28, and 54. (B) The input tree of representative genes involved in the cpxR circuit showing the isomorphisms that define the fibers. For each fiber, we show the number of paths of length $i-1$ at every layer of the input tree, $a_i$, and its branching ratio $n$. (C) Isomorphism between the input trees of baeR and spy. The input trees are composed of an infinite number of layers due to the autoregulation loop at baeR and cpxR. How does one prove the equivalence of two input trees when they have an infinite number of levels? A theorem proved by Norris (26) demonstrates that it suffices to find an isomorphism up to $N-1$ levels, where $N$ is the number of nodes in the circuit. Thus, in this case, two levels are sufficient to prove the isomorphism. (D) Symmetry fibration $\psi$ transforms the cpxR circuit $G$ into its base $B$ by collapsing the genes in the fibers into one. (E and F) Symmetry fibration of the fadR circuit (E) and its isomorphic input trees (F). Full list of genes in this circuit appears in SI Appendix, Table VI, ID nos. 3, 4, and 58. (G) Symmetric genes in the fiber synchronize their activity to produce the same activity levels. We use the mathematical model of gene regulatory kinetics from ref. 8 (sigmoidal interactions lead to qualitatively similar results) to show the synchronization inside the fiber baeR-spy when the fiber is activated by its regulator cpxR. Note that cpxR does not synchronize with the fiber.

Input Tree Representation.

In practice, the input tree of a gene is constructed as follows (SI Appendix, section IV.A). Consider the circuit in Fig. 1A. The input tree of gene spy depicted in Fig. 1B starts with spy at the root (first layer). Since this gene is upregulated by baeR and cpxR, then the second layer of the input tree contains these two pathways of length 1 starting at both genes. Gene baeR is further upregulated by cpxR and by itself through the autoregulation loop and cpxR is also autoregulated. Thus, the input tree continues to the third layer taking into account these three possible pathways of length 2 from the source gene to the spy gene. The procedure now continues, and since there are loops in the circuit, the input tree has an infinite number of layers.

The input tree formalism is a powerful framework to search for symmetries in information-processing networks, in that it replaces the canonical notion of a single trajectory with the set of all possible “histories” from an initial to a final state of the network, and this makes, in practice, it reasonably straightforward to “guess” a type of symmetry which is not apparent in the classical network framework. Based on results from refs. 13–16, we show in Symmetry Fibration Leads to Synchronization that if two input trees have the same “shape,” then the genes at the root of the input trees synchronize their activity (17–23), even though their input trees are made of different genes. This informal notion of equivalence is formalized by isomorphisms. An isomorphism between two input trees is a bijective map that preserves the topology of the input trees including the type of links. Specifically, a map $\tau :T\to T^{\prime }$ is an isomorphism if and only if for any pair of nodes $a$ and $b$ of $T$ connected by a link, the pair of nodes $\tau \left(a\right)$ and $\tau \left(b\right)$ of $T^{\prime }$ is connected by the same type of link (SI Appendix, section IV.B). In practice, this means that isomorphic input trees are “the same” except for the labeling of the nodes. Genes with isomorphic input trees are symmetric and synchronous. We quantify this result, next, by introducing the concept of symmetry fibration (13).

Symmetry Fibration of a Network.

The set of all input tree isomorphisms defines the symmetries of the network, which can be described by a “Grothendieck fibration” (12). The original Grothendieck definition of fibration is between categories (12), so the passage to a definition of fibration between graphs requires one to associate a category with a graph and rephrase Grothendieck’s definition in elementary terms. Different categories may be associated with a graph, giving rise to different notions of fibrations between graphs. The notion of fibration that we use henceforth has been introduced in computer science as a “surjective minimal graph fibration” (13, 15).

In general, a graph fibration $G=\left(N_G,E_G\right)$ is any morphism

$$\psi :G\to B$$ [1]

that maps $G$ to a graph $B=\left(N_B,E_B\right)$ (with $N_B$ nodes and $E_B$ edges) called the “base” of the graph fibration $\psi$ (SI Appendix, section IV.C). In this work we consider a surjective minimal graph fibration (13) which is a graph fibration $\psi$ that maps all nodes with isomorphic input trees, comprising a “fiber,” to a single node in $B$, thus producing the minimal base of the network. In this case, the base $B$ consists of a graph where all genes in a fiber have been collapsed into one representative node by the minimal fibration. Thus, a surjective minimal graph fibration, hereafter called symmetry fibration for the sake of lexical convenience, leads to a dimensional reduction of the network into its irreducible components. Crucially, a symmetry fibration is a dimensional reduction that preserves the dynamics in the network as we show next.

Symmetry Fibration Leads to Synchronization.

Next, we explain the connection between fibration and synchrony in a generality that is needed to justify our results following refs. 15 and 16. To describe the dynamical state of each gene in the transcriptional regulatory network, we first attach a phase space to each node in $G=\left(N_G,E_G\right)$ by considering a map $P:N_G\to M$ that assigns each node $i\in N_G$ to the phase space of the node denoted by the manifold $M$. For example, in a transcriptional regulatory network we assign to each gene $i\in N_G$ the phase space of real numbers $M=\mathbb{R}$. Then, the state of each gene is described by $x_i\left(t\right)\in \mathbb{R}$, representing the expression level of the gene $i$ at time $t$, which is typically measured by mRNA concentration of gene product. We then obtain the total phase space of $G$ as the product $PG={\prod }_{i\in N_G}P\left(i\right)$.

The fibers partition the graph $G$ into unique and nonoverlapping sets $\mathrm{\Pi }=\left\{{\mathrm{\Pi }}_1,\dots ,{\mathrm{\Pi }}_r\right\}$, such that ${\mathrm{\Pi }}_1\cup \cdots \cup {\mathrm{\Pi }}_r=G$ and ${\mathrm{\Pi }}_k\cap {\mathrm{\Pi }}_l=\varnothing$ if $k\ne l$ (24). We denote $i{\sim }_{\mathrm{\Pi }}j$ when the input trees of $i$ and $j$ are isomorphic and belong to the same fiber ${\mathrm{\Pi }}_k$. That is, $\exists k\hspace{0.17em}\mid \hspace{0.17em}i,j\in {\mathrm{\Pi }}_k$ and there exists a symmetry fibration that sends both nodes to the same node in the base, $\psi \left(i\right)=\psi \left(j\right)$. DeVille and Lerman (15) showed that symmetry fibrations induce robust synchronization in the system (theorem 4.3.1 in ref. 15). In particular, it was shown that if $\psi$ is a symmetry fibration, then—by proposition 2.1.12 in ref. 15—there exists a map ${\mathbb{P}}_{\psi }:PB\to PG$ that maps the total phase space of the base $B$, named $PB$, to the total phase space of the graph $G$. This map creates a polysynchronous subspace of synchronized solutions in fibers: ${\mathrm{\Delta }}_{\mathrm{\Pi }}=\left\{x\in PG\hspace{0.17em}\mid \hspace{0.17em}{x}_i\left(t\right)=x_j\left(t\right)\hspace{0.17em}\hspace{0.17em}\mathrm{w}\mathrm{h}\mathrm{e}\mathrm{n}\mathrm{e}\mathrm{v}\mathrm{e}\mathrm{r}\hspace{0.17em}\hspace{0.17em}\psi \left(i\right)=\psi \left(j\right)\right\}$, where each set of synchronous components of this subspace corresponds to a fiber in $\mathrm{\Pi }$ (lemma 5.1.1 in ref. 15; see also ref. 16). In other words, ${\mathrm{\Delta }}_{\mathrm{\Pi }}$ is a polysynchronous subspace of $PG$, such that components $x_i,x_j\in x$ synchronize (i.e., $x_i\left(t\right)=x_j\left(t\right)$) whenever the symmetry fibration $\psi$ sends them to the same node in $B$.

According to these results, we interpret synchronous genes to process the same information received through isomorphic pathways in the network, and, accordingly, we interpret a symmetry fibration as a transformation that preserves the dynamics of information flow since it collapses synchronous nodes in fibers (redundant from the point of view of dynamics) into a common base with identical dynamics to those of the fiber.

Synchronous nodes in a fiber induced by symmetry fibration correspond to the “minimal balanced coloring” in ref. 14. A balanced coloring assigns two nodes the same color only if their inputs, self-consistently, receive the same content of colored nodes, whence the term “balanced.” Thus, the flow of information arriving to genes in a fiber is analogous to a process of assigning a color to each gene such that each gene “receives” the colors from adjacent genes via incoming links and “sends” its color to the adjacent genes via its outgoing links. The nodes in a fiber have the same color symbolizing the fact that they synchronize. The nodes with the same color in the balanced coloring partition (14) correspond to fibers induced by symmetry fibrations (15). We use the minimal balanced coloring algorithm proposed in ref. 25 for the computation of minimal bases (24) to find fibers (SI Appendix, section V).

Strongly Connected Components of the E. coli Network.

The input trees in the E. coli cpxR circuit are displayed in Fig. 1B. The input trees of baeR and spy are isomorphic and define the baeR-spy fiber (Fig. 1C). We call this circuit a feedforward fiber (FFF). The input tree of cpxR is not isomorphic to either baeR or spy, and therefore cpxR is not symmetric with these genes, but it is isomorphic to bacA, slt, and yebE forming another fiber. Likewise, genes ung, tsr, and psd are all isomorphic, composing another fiber (Fig. 1B). Fig. 1D shows the symmetry fibration $\psi :G\to B$ that collapses the genes in the fibers to the base $B$. Fig. 1E shows another example (of many) of a single connected component, fadR, and its corresponding isomorphic input trees (Fig. 1F), fibers, and base.

The dynamical state of a gene is encoded in the topology of the input tree. In turn, this topology is encoded by a sequence, $a_i$, defined as the number of genes in each $i$th layer of the input tree (Fig. 1B). The sequence $a_i$ represents the number of paths of length $i-1$ that reach the gene at the root. This sequence is characterized by the branching ratio $n$ of the input tree defined as $a_{i+1}/a_i\underset{i\to \infty }{\to }n$, which represents the multiplicative growth of the number of paths across the network reaching the gene at the root. For instance, the input trees of genes baeR-spy (Fig. 1B) encode a sequence $a_i=i$ with branching ratio $n=1$ representing the single ($n$ = 1) autoregulation loop inside the fiber.

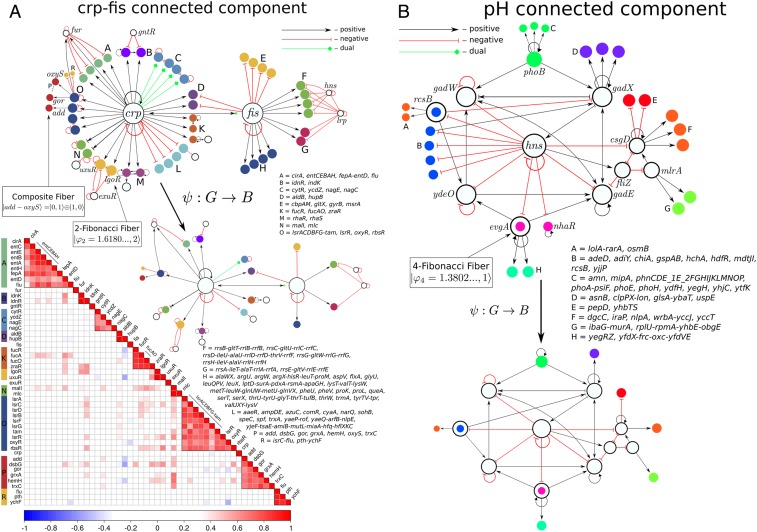
Beyond several single-gene strongly connected components like those shown in Fig. 1, we find that the E. coli network has other strongly connected components (in a strongly connected component, each gene is reachable from every other gene; SI Appendix, section VI), three in total, which regulate more involved topologies of fibers. We find 1) a two-gene strongly connected component composed of master regulators crp-fis involved in a myriad of functions like carbon utilization (Fig. 2 A, Top), 2) a five-gene strongly connected component involved in the stress response system (SI Appendix, Fig. S7), and 3) the largest strongly connected component at the core of the network which is composed of genes involved in the pH system that regulate hydrogen concentration (Fig. 2B). Each of these three components regulates a rich variety of fiber topologies which are collapsed into the base by the symmetry fibration $\psi :G\to B$, as shown in Fig. 2B.

Fig. 2.

Strongly connected components of the genetic network and synchronization of gene coexpression in the fibers in E. coli. (A, Top) Two-gene connected component of crp-fis. This component controls a rich set of fibers as shown. We also show the symmetry fibration collapsing the graph to the base. We highlight the fiber uxuR-lgoR which sends information to its regulator exuR and forms a 2-Fibonacci fiber $\left|{\phi }_2=1.6180..,\ell =2\right.⟩$, as well as the double-layer composite $\left|add-oxyS\right.⟩=\left|\mathrm{0,1}\right.⟩\oplus \left|\mathrm{1,1}\right.⟩$. (A, Bottom) Coexpression correlation matrix calculated from the Pearson coefficient between the expression levels of each pair of genes in A, Top. Synchronization of the genes in the respective fibers is corroborated as the block structure of the matrix. (B) The core of the E. coli network is the strongly connected component formed by genes involved in the pH system as shown. This component supports two Fibonacci fibers: 3-FF and 4-FF and fibers as shown. Open colored circles indicate genes that are in fibers and also belong to the pH component.

Fiber Building Blocks.

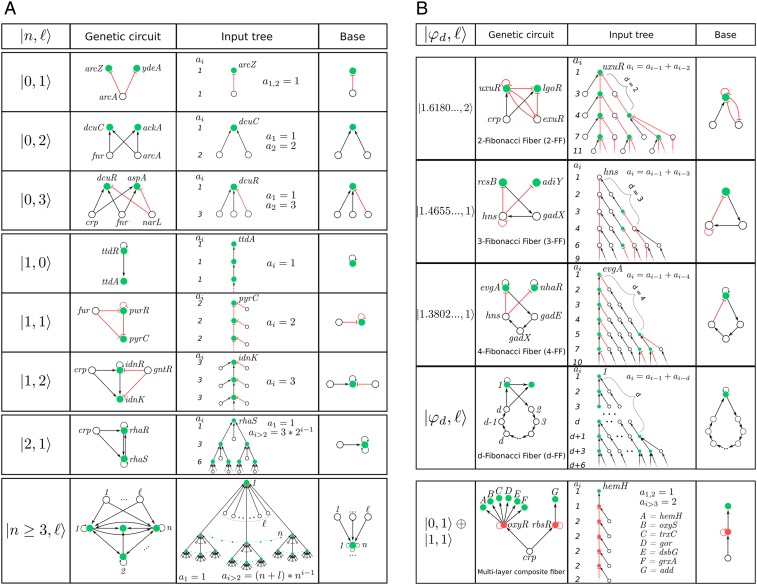
We find that the transcriptional regulatory network of E. coli is organized in 91 different fibers. The complete list of fibers in E. coli is shown in SI Appendix, section VII and Table VI and the statistics are shown in SI Appendix, Table I. Plots of each fiber are shown in Dataset S1. We find a rich variety of topologies of the input trees. Despite this diversity, the input trees present common topological features that allow us to classify all fibers into concise classes of fundamental “fiber building blocks” (Fig. 3 A and B). We associate a building block to a fiber by considering the genes in the fiber plus the external incoming regulators of the fiber plus the minimal number of their regulators in turn that are needed to establish the isomorphism in the fiber. When the fiber is connected to any external regulator, either via a direct link or through a path in the strongly connected component forming a cycle, then the genes in this cycle are considered part of the building block of the fiber, since such a cycle is crucial to establish the dynamical synchronization state (when there is more than one cycle, the shortest cycle is considered).

Fig. 3.

Classification of building blocks in E. coli. (A) Basic fiber building blocks. These building blocks are characterized by a fiber that does not send back information to its regulator. They are characterized by two integer fiber numbers: $\left|n,\ell \right.⟩$. We show selected examples of circuits and input trees and bases. The full list of fibers appears in SI Appendix, Table VI and Dataset S1. The statistical count of every class is in SI Appendix, Table I. Bottom example shows a generic building block for a general n-ary tree $\left|n,\ell \right.⟩$ with $\ell$ regulators. (B) Complex Fibonacci and multilayer building blocks. These building blocks are more complex and characterized by an autoregulated fiber that sends back information to its regulator. This creates a fractal input tree that encodes a Fibonacci sequence with golden branching ratio in the number of paths $a_i$ versus path length, $i-1$. When the information is sent to the connected component that includes the regulator, then a cycle of length $d$ is formed and the topology is a generalized Fibonacci block with golden ratio ${\phi }_d$ as indicated. We find three such building blocks: 2-FF, 3-FF, and 4-FF. Bottom panel shows a multilayer composite fiber with a feedforward structure.

We find that the most basic input tree topologies can be classified by integer “fiber numbers” $\left|n,\ell \right.⟩$ reflecting two features: 1) infinite $n$-ary trees with branching ratio $n$ representing the infinite pathways going through $n$ loops inside the base of the fiber and 2) finite trees representing finite pathways starting at $\ell$ external regulators of the fiber. The most basic fibers in E. coli have three values of $n=\mathrm{0,1,2}$ (Fig. 3A): 1) fibers with $n=0$ loops, called star fibers (SF); 2) fibers with $n=1$ loop, called chain fibers (CF); and 3) fibers with $n=2$ loops, called binary-tree fibers (BTF). This classification does not take into account the types of repressor or activator links in the building blocks, which lead to further subclasses of fibers that determine the type of synchronization (fixed point, limit cycles, etc.) and thus the functionality of the fibers.

Fig. 3A shows a sample of dissimilar circuits that can be concisely classified by $\left|n,\ell \right.⟩$ (full list in Dataset S1). For instance, the $n=0$ SF class includes dissimilar circuits like $\left|arcZ-ydeA\right.⟩=\left|\mathrm{0,1}\right.⟩$, $\left|dcuC-ackA\right.⟩=\left|\mathrm{0,2}\right.⟩$, which is a bifan network motif (2), and generalizations with $\ell =3$ regulators like $\left|dcuR-aspA\right.⟩=\left|\mathrm{0,3}\right.⟩$ (Fig. 3 A, Top). The main feature of these building blocks is that they do not contain loops and therefore the input trees are finite. The CF class contains $n=1$ loop in the fiber and therefore an infinite chain in the input tree, like the autoregulated loop in the fiber $\left|ttdR\right.⟩=\left|\mathrm{1,0}\right.⟩$. We note that while the input tree is infinite, the topological class is characterized by a single number $n=1$ concisely represented in the base. Furthermore, a theorem proved by Norris (26) demonstrates that it suffices to test $N_G-1$ layers of the input trees to prove isomorphism, even though the input tree may contain an infinite number of layers. Adding one external regulator ($\ell =1$) to this circuit converts it to the purine fiber $\left|purR\right.⟩=\left|\mathrm{1,1}\right.⟩$ which is an example of a FFF, like the baeR circuit in Fig. 1A. This circuit resembles a feedforward loop motif (2), but it differs in the crucial addition of the autoregulator loop at purR that allows genes purR and pyrC to synchronize. When another external regulator is added, we find the idonate fiber $\left|idnR\right.⟩=\left|\mathrm{1,2}\right.⟩$. More elaborated circuits contain two autoregulated loops and feedback loops featuring trees with branching ratio $n=2$.

Fibonacci Fibers.

So far we have analyzed building blocks that receive information from the external regulators in their respective strongly connected components, but do not send back information to the external regulators. These topologies are characterized by integer branching ratios, $n=\mathrm{0,1,2}$, as shown in Fig. 3A. We find, however, more interesting building blocks that also send information back to their regulators. These circuits contain additional cycles in the building blocks that transform the input trees into fractal trees characterized by noninteger fractal branching ratios. Notably, the building block of the fiber uxuR-lgoR that is regulated by the connected component crp-fis (Fig. 2) forms an intricate input tree (Fig. 3 B, Top) where the number of paths of length $i-1$ is encoded in a Fibonacci sequence $a_i=$ 1, 3, 4, 7, 11, 18, 29, … characterized by the Fibonacci recurring relation $a_1=1$, $a_2=3$, and $a_i=a_{i-1}+a_{i-2}$ for $i>2$. This sequence leads to the noninteger branching ratio known as the golden ratio: $a_{i+1}/a_i\underset{i\to \infty }{\to }\phi =\left(1+\sqrt{5}\right)/2=1.6180..$.

This topology arises in the genetic network due to the combination of two cycles of information flow. First, the autoregulation loop inside the fiber at uxuR creates a cycle of length $d=1$ which contributes to the input tree with an infinite chain with branching ratio $n=1$. This sequence is reflected in the Fibonacci series by the term $a_i=a_{i-1}$. The important addition to the building block is a second cycle of length $d=2$ between uxuR in the fiber and its regulator exuR: uxuR $\to$ exuR $\to$ uxuR. This cycle sends information from the fiber to the regulator and back to the fiber by traversing a path of length $d=2$ that creates a “delay” of $d=2$ steps in the information that arrives back to the fiber (Fig. 3 B, Top). This short-term “memory” effect is captured by the second term $a_i=a_{i-2}$ in the Fibonacci sequence leading to $a_i=a_{i-1}+a_{i-2}$ and the golden ratio. We call this topology a Fibonacci fiber (FF).

This argument implies that an autoregulated fiber that further regulates itself by connecting to its connected component via a cycle of length $d$ encodes a generalized Fibonacci sequence of order $d$ defined as $a_i=a_{i-1}+a_{i-d}$ with generalized golden ratio ${\phi }_d$ (Fig. 3 B, Top, fourth row). We find such a Fibonacci sequence in the evgA-nhaR fiber building block linked to the pH strongly connected components shown in Fig. 2B. This fiber contains an autoregulation cycle inside the fiber and also an external cycle of length $d=4$ through the pH strongly connected component: evgA $\to$ gad E $\to$ gadX $\to$ hns $\to$ evgA (Fig. 3 B, Top, third row). This topology forms a fractal input tree with sequence $a_i=a_{i-1}+a_{i-4}$ (sequence A003269 in ref. 27) and branching golden ratio ${\phi }_4=1.38028..$. We call this topology 4-Fibonacci fiber, 4-FF. Generalized Fibonaccis appear inside strongly connected components, like the rcsB-adiY 3-FF in the pH system (Fig. 3 B, Top, second row). Likewise, if the network contains many cycles of varying length up to a maximum $d$, the Fibonacci sequence generalizes to $a_i=a_{i-1}+a_{i-2}+\cdots +a_{i-1-d}+a_{i-d}$, and the branching ratio satisfies $d=-\frac{\log \left(2-{\phi }_d\right)}{\log {\phi }_d}$ (28).

Multilayer Composite Fibers.

Building blocks can also be combined to make composite fibers, like prime numbers or quarks can be combined to form natural numbers or composite particles like protons and neutrons, respectively. The ability to assemble fiber building blocks to make larger composites is important in that it helps to understand systematically higher-order functions of biological systems composed of many genetic elements. We discover a particular type of composite made up of two elementary building blocks that we name multilayer composite fiber. For instance, the double-layer add-oxyS fiber in the crp-fis connected component (Figs. 2A and 3 B, Bottom and ID 7 in SI Appendix, Table VI and Dataset S1) is a composite $\left|add-oxyS\right.⟩=\left|\mathrm{0,1}\right.⟩\oplus \left|\mathrm{1,1}\right.⟩$ made of a series of genes composing a single fiber of type $\left|\mathrm{0,1}\right.⟩=\left|add,dsbG,gor,grxA,hemH,oxyS,trxC\right.⟩$ that are regulated by two different transcription factors rbsR and oxyR that form another fiber of type $\left|\mathrm{1,1}\right.⟩=\left|rbsR,oxyR\right.⟩$. This composite is of importance since it allows for information to be shared between two genes, for instance add and oxyS, which are not directly connected (in this case, separated by a distance in the network of length 2 from crp).

Composite fibers satisfy a simple engineering “sum rule”: elementary fibers are composed in series of fibers in a predefined order where the first layer is represented by an entry fiber (carrying transcription factors), and the last layer is formed by a terminator fiber of output genes (encoding enzymes), as shown in Fig. 3 B, Bottom. This multilayer composite fiber is biologically significant because genes in the output layer synchronize a genetic module that implements the same function even though the genes in the module are not directly connected and, indeed, can be at far distances in the network. Such functionally related modules could not be identified by modularity algorithms (29) which cluster nodes in modules of highly connected nodes.

We find that composite fibers are dominant in eukaryotes (yeast, mice, humans; see Fibration Landscape across Biological Networks, Species, and System Domains). They resemble the building blocks of multilayered deep neural networks where each subsequent gene in the layer synchronizes despite the fact that nodes can be distant in the network. More generally, composite fibers with multiple layers streamline the construction of larger aggregates of fibration building blocks, performing more complex function in a coordinated fashion. These composite topologies complete the classification of input trees.

Fibration Landscape across Biological Networks, Species, and System Domains.

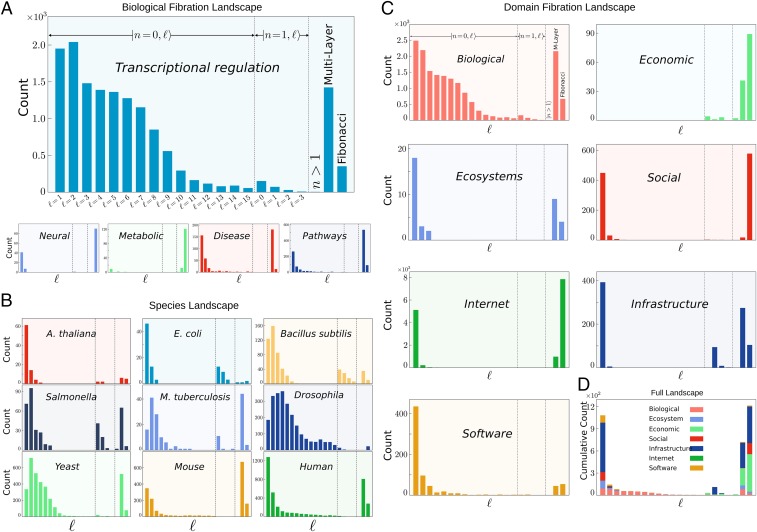
To study the applicability of fibration symmetries across domains of complex networks we have analyzed 373 publicly available datasets (SI Appendix, section VIII). Full details of each network and results can be accessed on GitHub at https://github.com/makselab/fibrationData/blob/master/datasets.xlsx. The codes to reproduce this analysis are on GitHub at https://github.com/makselab (SI Appendix, section V). The full datasets are on GitHub at https://github.com/makselab/fibrationData/blob/master/rawData.zip. We analyze biological networks spanning from transcriptional regulatory networks, metabolic networks, cellular processes networks and signaling pathways, disease networks, and neural networks. We span different species ranging from Arabidopsis thaliana, E. coli, Bacillus subtilis, Salmonella enterica, Mycobacterium tuberculosis, Drosophila melanogaster, Saccharomyces cerevisiae (yeast), and Mus musculus (mouse) to Homo sapiens (human). The topological fiber numbers $\left|n,\ell \right.⟩$ allow us to systematically classify fibers across the different domains in a unifying way. We find that fibration symmetries are found across all biological processes and domains. The fiber distributions for each type of biological network calculated by summing over the studied species are displayed in Fig. 4A and the fiber distributions for each species calculated over the type of biological networks are shown in Fig. 4B. Our analysis allows us to investigate the specific attributes and commonalities of the fiber building blocks inside and across biological domains. We find a varied set of fibers that characterize the biological landscape. Certain features of the fiber number distribution are visible in the transcriptional networks in Fig. 4A. For instance, a tail with $\ell$ is seen in the $n=0$ class as well as in the $n=1$ class. Across species (Fig. 4B), bacteria like E. coli or B. subtilus display a majority of $n=0$ building blocks, while higher-level organisms like yeast, mice, and humans display a majority of more complex building blocks like multilayers and Fibonaccis.

Fig. 4.

Fibration landscape across domains and species. (A) Fibration landscape for biological networks. Shown is the total number of fiber building blocks across five types of biological networks analyzed in the present work. The count includes the total number of fibers in the networks of each biological type considering all species analyzed for each type (SI Appendix, Table IV). (B) Fibration landscape across species. Shown is the count of fibers across each analyzed species. Each panel shows the count over the different types of biological networks (E. coli contains only the transcriptional network; see SI Appendix, Table IV). (C) Fibration landscape across domains. Shown is the count of fibers across the major domains studied. The biological domain panel is calculated over all networks and species in A and B. (D) Global fibration landscape. Shown is the cumulative count of fibers in all domains in C. The cumulative count represents the total number of fibers per network of $10^4$ nodes. Specifically, the quantity is calculated as the total number of fibers divided by the total number of nodes in all networks per domain multiplied by $10^4$.

To test the existence of symmetry fibrations across other domains we extend our studies to complex networks beyond biology ranging from social, infrastructure, internet, software, and economic networks to ecosystems (details of datasets in SI Appendix, section VIII). Fig. 4C shows the obtained fiber distributions for each domain. A normalized comparison across domains is visualized in Fig. 4D, showing the cumulative number of fibers over all domains and species per network size of ${\mathrm{10}}^4$ nodes. The results support the applicability of the concept of symmetry fibration beyond biology to describe the building blocks of networks across all domains.

Gene Coexpression and Synchronization via Symmetry Fibration.

We have shown in Symmetry Fibration Leads to Synchronization that fibers in networks determine cluster synchronization in the dynamical system. In a gene regulatory network, symmetric genes in a fiber synchronize their activity to produce gene coexpression levels that sustain cellular functions. We corroborate this result numerically in Fig. 1G in the particular example of the baeR-spy FFF in E. coli, and this result applies to all fibers, irrespective of the dynamical system law.

To exemplify the synchronization in fibers, we consider the dynamics in the composite fiber $\left|add-oxyS\right.⟩=\left|\mathrm{0,1}\right.⟩\oplus \left|\mathrm{1,1}\right.⟩$ depicted in Figs. 2A and 3 B, Bottom, which is composed of autoregulator $1=crp$, and two layers of fibers: $2=rbsR$, $3=oxyR$ and $4=add$, $5=oxyS$ (we consider here a reduced fiber for simplicity, and we add the autoregulator to crp to the building block for completeness). Graph $G=\left\{N_G,E_G\right\}$ consists of $N_G=\left\{\mathrm{1,2,3,4,5}\right\}$, $E_G=\left\{1\to \mathrm{1,1}\to \mathrm{2,1}\to \mathrm{3,2}⊣\mathrm{2,3}⊣\mathrm{3,2}\to \mathrm{4,3}\to 5\right\}$ ($⊣$ refers to repressor and $\to$ to activation), and a five-dimensional total phase space $PG={\mathbb{R}}^5$ with state vector $X\left(t\right)=\left\{x_1\left(t\right),x_2\left(t\right),x_3\left(t\right),x_4\left(t\right),x_5\left(t\right)\right\}$ describing the expression levels of each gene’s product (e.g., mRNA concentration).

The symmetry fibration $\psi :G\to B$ collapses the graph $G$ into the base $B=\left\{N_B,G_B\right\}$, where $N_B=\left\{a,b,c\right\}$ and $E_B=\left\{a\to a,a\to b,b⊣b,b\to c\right\}$. The symmetry fibration acts on the nodes $\psi \left(1\right)=a$, $\psi \left(2\right)=\psi \left(3\right)=b$, and $\psi \left(4\right)=\psi \left(5\right)=c$ and on the edges $\psi \left(1\to 1\right)=a\to a$, $\psi \left(1\to 2\right)=\psi \left(1\to 3\right)=a\to b$, $\psi \left(2⊣2\right)=\psi \left(3⊣3\right)=b⊣b$, and $\psi \left(2\to 4\right)=\psi \left(3\to 5\right)=b\to c$. Thus, the fibers partition the graph $G$ as $\mathrm{\Pi }=\left\{{\mathrm{\Pi }}_a,{\mathrm{\Pi }}_b,{\mathrm{\Pi }}_c\right\}$, where ${\mathrm{\Pi }}_a=\left\{1\right\}$, ${\mathrm{\Pi }}_b=\left\{\mathrm{2,3}\right\}$, and ${\mathrm{\Pi }}_c=\left\{\mathrm{4,5}\right\}$.

We represent the dynamics by two functions $k\left(x\right)$ and $g\left(x\right)$ modeling degradation and synthesis of gene product, respectively (9, 10). For example, $k\left(x\right)$ can be modeled as a linear degradation term and $g_i\left(x\right)$ as a Hill function ($i=A,R$, activation or repression) (9). We consider that multiple inputs are combined by multiplying functions $g\left(x\right)$, but any other way of combining inputs can be used. Then, the dynamics of the expression levels of the genes in the circuit are described by ref. 14:

$$\left\{\begin{array}{c}\frac{d{x}_1}{dt}=-k\left(x_1\right)+g_A\left(x_1\right)\hfill \\ \frac{d{x}_2}{dt}=-k\left(x_2\right)+g_A\left(x_1\right)\hspace{0.17em}*\hspace{0.17em}{g}_R\left(x_2\right)\hfill \\ \frac{d{x}_3}{dt}=-k\left(x_3\right)+g_A\left(x_1\right)\hspace{0.17em}*\hspace{0.17em}{g}_R\left(x_3\right)\hfill \\ \frac{d{x}_4}{dt}=-k\left(x_4\right)+g_A\left(x_2\right)\hfill \\ \frac{d{x}_5}{dt}=-k\left(x_5\right)+g_A\left(x_3\right).\hfill \end{array}\right.$$ [2]

The dynamics of the base are described by the state vector of the base: $\left(y_a\left(t\right),y_b\left(t\right),y_c\left(t\right)\right)$ with dynamical equations (16):

$$\left\{\begin{array}{c}\frac{d{y}_a}{dt}=-k\left(y_a\right)+g_A\left(y_a\right)\hfill \\ \frac{d{y}_b}{dt}=-k\left(y_b\right)+g_A\left(y_a\right)\hspace{0.17em}*\hspace{0.17em}{g}_R\left(y_b\right)\hfill \\ \frac{d{y}_c}{dt}=-k\left(y_c\right)+g_A\left(y_b\right).\hfill \end{array}\right.$$ [3]

If $\left(y_a\left(t\right),y_b\left(t\right),y_c\left(t\right)\right)$ is a solution for the base Eq. 3, then the map ${\mathbb{P}}_{\psi }$ sends the phase space of this base to the phase space of the solutions in the graph $G$ (16):

$$\begin{array}{ll}\hfill & \left(x_1\left(t\right),x_2\left(t\right),x_3\left(t\right),x_4\left(t\right),x_5\left(t\right)\right)\hfill \\ \hfill & ={\mathbb{P}}_{\psi }\left[y_a\left(t\right),y_b\left(t\right),y_c\left(t\right)\right]=\left(y_a\left(t\right),y_b\left(t\right),y_b\left(t\right),y_c\left(t\right),y_c\left(t\right)\right).\hfill \end{array}$$ [4]

Therefore, the graph $G$ sustains a polysynchronous subspace (see for instance motivating example 1.4 in ref. 15):

$$\begin{array}{ll}\hfill {\mathrm{\Delta }}_{\mathrm{\Pi }}& =\left\{\left(x_1,x_2,x_3,x_4,x_5\right)\in {\mathbb{R}}^5\mid x_1\left(t\right),x_2\left(t\right)=x_3\left(t\right),x_4\left(t\right)\right.\hfill \\ \hfill & =\left.x_5\left(t\right)\right\}.\hfill \end{array}$$ [5]

This result can be corroborated by simply plugging $\left(x_1\left(t\right),x_2\left(t\right),x_3\left(t\right)=x_2\left(t\right),x_4\left(t\right),x_5\left(t\right)=x_4\left(t\right)\right)$ into Eq. 2 to obtain a solution of the dynamics, implying the synchrony $x_2\left(t\right)=x_3\left(t\right)$ in fiber ${\mathrm{\Pi }}_b$ and $x_4\left(t\right)=x_5\left(t\right)$ in fiber ${\mathrm{\Pi }}_c$. We note that the concept of sheaves and stacks might be useful to generalize the symmetry fibration framework to multiplex networks.

We test this gene synchronization with publicly available transcription profile experiments available from the literature. We use gene expression data profiles in E. coli compiled at Ecomics: http://prokaryomics.com (30). This portal collects microarray and RNA-seq experiments from different sources such as the NCBI Gene Expression Omnibus (GEO) public database (31) and ArrayExpress (32) under different experimental growth conditions. The data are also compiled at the Colombos web portal (33). The database contains transcriptome experiments measuring the expression level of 4,096 genes in E. coli strains over 3,579 experimental conditions which are described as strain, medium, stress, and perturbation. Raw data are preprocessed to obtain expression levels by using noise reduction and bias correction to normalize data across different platforms (30).

E. coli can adapt its growth to the different conditions that it finds in the medium. This adaptation is made by sensing extra and intracellular molecules and using them as effectors to activate or repress transcription factors. This implies that the different fibers are activated by specific experimental conditions. The Ecomics portal allows one to obtain those experimental conditions where a set of genes has been significantly expressed under a particular set of conditions. We perform standard gene expression analysis (http://colombos.net and ref. 33) of the expression levels in E. coli obtained under these conditions.

For a given set of genes in a fiber, we find the experimental conditions for which the genes have been significantly expressed by comparing the expression samples over the 1,576 different WT growth conditions. Following ref. 33, the experimental conditions are ranked with the inverse coefficient of variation (ICV) defined as ${\text{ICV}}_k=\left|{\mu }_k\right|/{\sigma }_k$, where ${\mu }_k$ is the average expression level of the genes in the condition $k$ and ${\sigma }_k$ is the SD. Following ref. 33, we select those conditions with ${\mathrm{I}\mathrm{C}\mathrm{V}}_k>⟨{\text{ICV}}_k⟩$, i.e., where the average expression levels in the particular condition $k$ are significantly higher than the SD. This score reflects the fact that, in a relevant condition, the genes show an increment of their expression above the individual variations caused by random noise. Details on the expression analysis can be found in ref. 33 and https://doi.org/10.1371/journal.pone.0020938.s001. Thus, we obtain expression levels organized by the relevant experimental conditions which are labeled according to the GEO database (31). From these data, we calculate the coexpression matrix using the Pearson correlation coefficient between the expression levels of two genes $i$ and $j$ in the relevant conditions for genes in a fiber. For off-diagonal correlations between genes in different fibers, we use the combined sets of conditions of both genes.

Results for the correlation matrix are shown in Fig. 2 A, Bottom for fibers regulated by the crp-fis strongly connected component. Gene expression is obtained for every gene, so we plot the correlation matrix calculated over each pair of genes. Genes that belong to the same operon are transcribed as a single unit by the same mRNA molecule, so these genes are expected to trivially synchronize (variations exist due to attenuators inside the operon). Thus, we group together these genes as operons in Fig. 2A to indicate this trivial synchronization. To test the existence of fiber synchronization we compare gene coexpression belonging to different operons. Fig. 2 A, Bottom shows that expression levels of the genes that belong to a fiber are highly correlated as predicted by the symmetry fibration. Genes that belong to different fibers show no significant correlations among them. In particular, there is no significant correlation between the expression of genes in a given fiber and the two master regulators crp and fis. This result is consistent with the fibration symmetry and occurs despite the fact that both crp and fis directly regulate all genes in the studied fibers. We find some off-diagonal weak correlations between fibers (e.g., malI), probably indicating missing links or missing regulatory processes that produce extra synchronizations. Some genes present weak correlations inside fibers (e.g., cirA), indicating weak symmetry breaking probably from asymmetries in the strength of binding rate of transcription factors or input functions, effects that are not considered in the topological view of the input trees and can lead to desynchronization inside the fiber.

Discussion

Fibration symmetries make sure that genes are turned on and off at the right amount to ensure the synchronization of expression levels in the fiber needed to execute cellular functions. In the fibration framework, network function can be pictured as an orchestra in which each instrument is a gene in the network. When the instruments play coherently, with structured temporal patterns, the network is functional. Here we have concentrated on the simplest temporal organization, one in which some units (instruments) act synchronously in time, a ubiquitous pattern observed in all biological networks. Our findings identify the symmetries that predict this synchronization and give rise to functionally related genes from the fibrations of the genetic network.

Unlike network motifs which are identified by statistical overrepresentation (2), fibers in biology arise from principles of symmetries following the tradition of how the building blocks of elementary particles have being discovered in physics and geometry (5). Our first principle approach to identify building blocks is based on the circuit’s theoretical and practical (rather than statistical) significance to serve minimal forms of coherent function and logic computation.

Further results shown in ref. 34 indicate that symmetries also describe the structure of neural connectomes and these symmetries factorize according to function. Thus, symmetries can be used to systematically organize biological diversity into building blocks using invariances in the information flow encoded in the topologies of the input trees. Genes related by symmetries are coexpressed, thus providing a functional rationale for the biological existence of these symmetries.