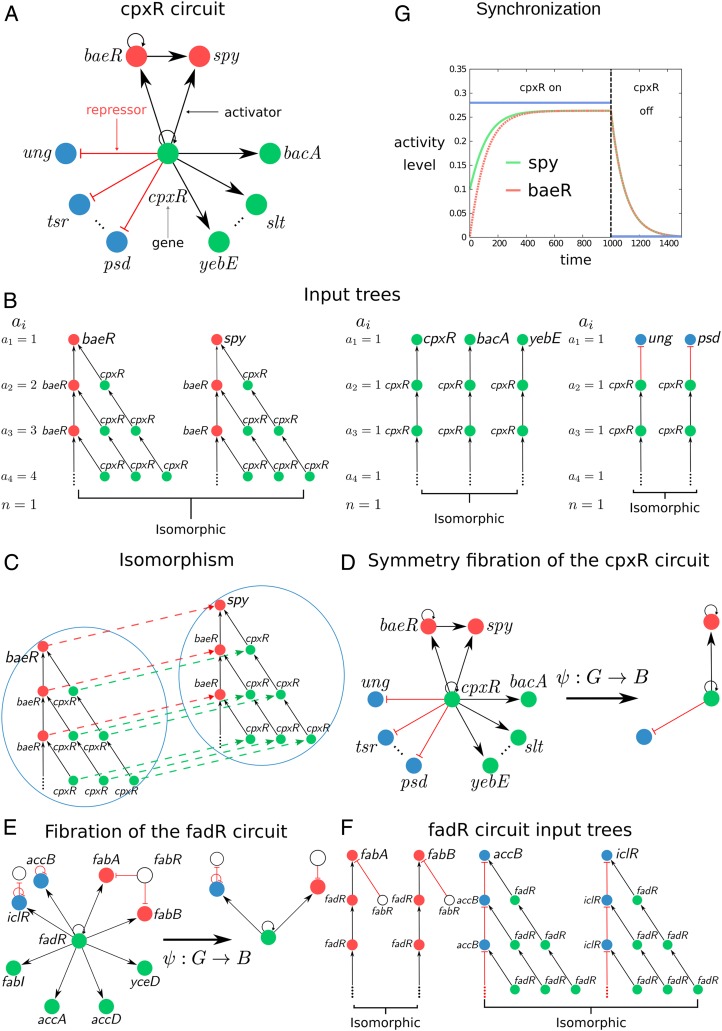
Fig. 1.

Definition of input tree, symmetry fibration, fiber, and base. (A) The circuit controlled by the cpxR gene regulates a series of fibers as shown by the different-colored genes. The circuit regulates more genes represented by the dotted lines which are not displayed for simplicity. The full lists of genes and operons in this circuit are in SI Appendix, Table VI, ID nos. 27, 28, and 54. (B) The input tree of representative genes involved in the cpxR circuit showing the isomorphisms that define the fibers. For each fiber, we show the number of paths of length $i-1$ at every layer of the input tree, $a_i$, and its branching ratio $n$. (C) Isomorphism between the input trees of baeR and spy. The input trees are composed of an infinite number of layers due to the autoregulation loop at baeR and cpxR. How does one prove the equivalence of two input trees when they have an infinite number of levels? A theorem proved by Norris (26) demonstrates that it suffices to find an isomorphism up to $N-1$ levels, where $N$ is the number of nodes in the circuit. Thus, in this case, two levels are sufficient to prove the isomorphism. (D) Symmetry fibration $\psi$ transforms the cpxR circuit $G$ into its base $B$ by collapsing the genes in the fibers into one. (E and F) Symmetry fibration of the fadR circuit (E) and its isomorphic input trees (F). Full list of genes in this circuit appears in SI Appendix, Table VI, ID nos. 3, 4, and 58. (G) Symmetric genes in the fiber synchronize their activity to produce the same activity levels. We use the mathematical model of gene regulatory kinetics from ref. 8 (sigmoidal interactions lead to qualitatively similar results) to show the synchronization inside the fiber baeR-spy when the fiber is activated by its regulator cpxR. Note that cpxR does not synchronize with the fiber.