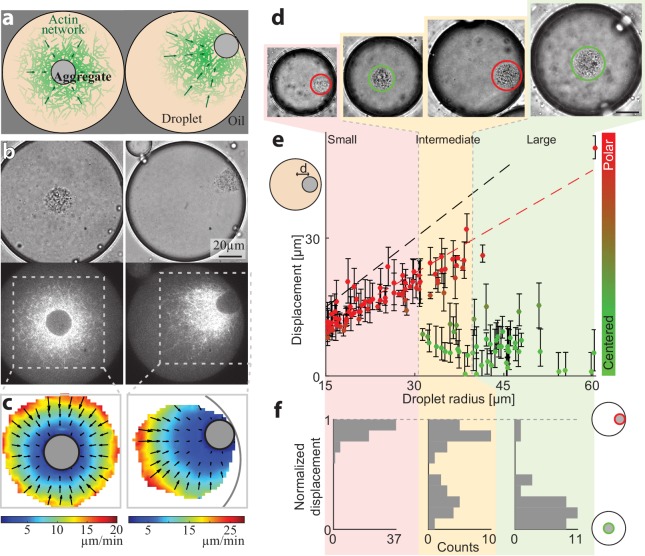
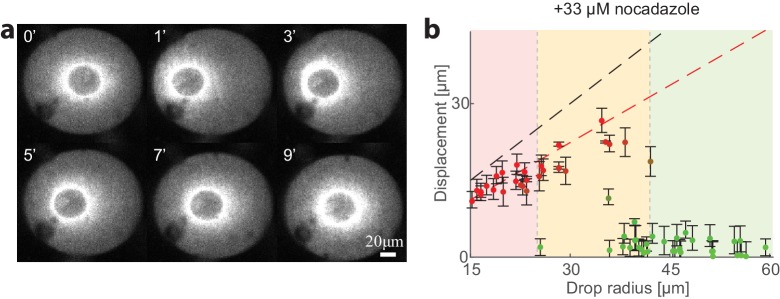
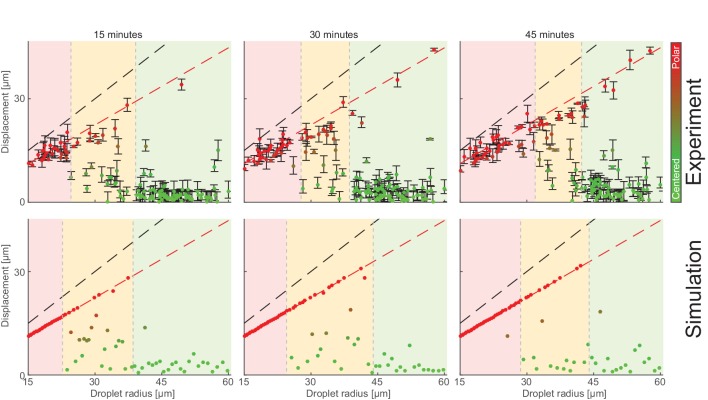
Figure 1. Size-dependent localization of the contraction center.

(a) Schematic illustration of the two stable configurations of the system: a symmetric state with a centered aggregate (left), and a polar state in which the aggregate is positioned near the droplet’s boundary (right). (b) Bright-field (top) and spinning disk confocal (bottom) images of the equatorial cross section of droplets in a symmetric state (left; Video 1) and a polar state (right; Video 2). The aggregate is visible both in the bright-field images, and as an exclusion zone surrounded by regions of high actin network density in the florescence images. The actin network is labeled with GFP-Lifeact. (c) The actin network velocity field as determined by correlation analysis of the time lapse movies of the symmetric and polar droplets in (b). The network exhibits contractile flows directed toward the aggregate in both cases. (d–f) The position of the aggregate surrounding the contraction center was determined for a population of droplets of different sizes, 40 min after sample preparation. (d) Bright-field images of droplets of different sizes. The aggregate position in each droplet was determined from the images, and its displacement from the droplet’s center was measured (see Materials and methods). (e) The displacement of the aggregate from the center is plotted as a function of droplet radius. The dashed black line marks the droplet radius, and the dashed red line marks the displacement where the aggregate reaches the boundary (droplet radius minus aggregate radius). (f) Histograms of the aggregates localization for droplets in different size ranges: small, intermediate and large (Materials and methods). The distance of the aggregate from the center of the droplet was normalized to be between 0 (centered) and 1 (polar). Small droplet (R < 31 µm) are polar (red; left). Intermediate droplets (31 µm < R < 40 µm) exhibit a bipolar distribution with both symmetric and polar droplets (yellow; center). Large droplet (40 µm < R) are symmetric (green; right).

Figure 1—figure supplement 1. Contraction center localization and centering dynamics are not dependent on microtubules.

Aggregate positions and recentering dynamics were measured in droplets supplemented with 33 μM Nocodazole, which disrupts microtubule assembly. (a) Spinning-disk confocal images from a timelapse movie showing the recentering of the contraction center following a magnetic perturbation in a droplet with Nocodazole-treated extract. The actin network is labeled with GFP-Lifeact. (b) The position of the aggregate surrounding the contraction center was determined for a population of droplets formed with Nocodazole-treated extract. The displacement of the aggregate from the center is plotted as a function of droplet radius for unperturbed droplets. The colored regions depict the different size ranges: small droplets that are primarily polar (red), intermediate range with both polar and symmetric droplets (yellow), and large droplets which are mostly centered (green). The centering dynamics and localization distribution are similar to the untreated condition (Figures 1 and 3).

Figure 1—figure supplement 2. Size-dependent localization of the contraction center as a function of time.

The position of the aggregate surrounding the contraction center was determined for a population of droplets of different sizes, 15 min (left), 30 min (center) or 45 min (right) after sample preparation. The displacement of the aggregate from the center is plotted as a function of droplet radius based on the experimental data (top) and the simulation (bottom; see Appendix 2). The colored regions depict the different size ranges: small droplets that are primarily polar (red), intermediate range with both polar and symmetric droplets (yellow), and large droplets which are mostly centered (green). The dashed black line marks the droplet radius, and the dashed red line marks the displacement where the aggregate reaches the boundary (droplet radius minus aggregate radius). The centered state is metastable, with larger droplets becoming polar over time.