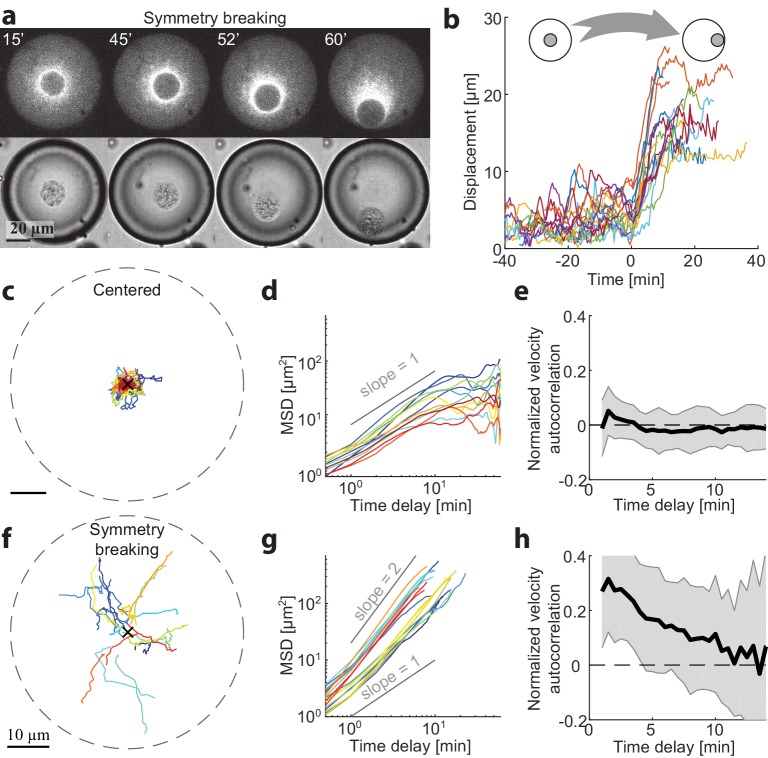
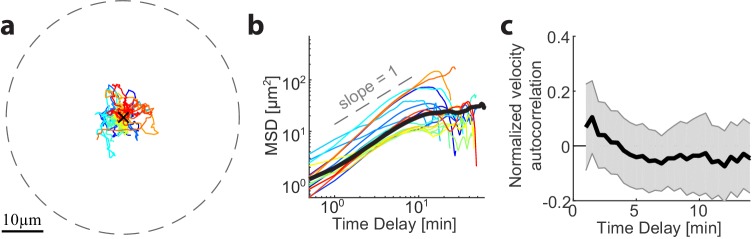
Figure 2. Dynamics of centering and symmetry breaking.

The dynamics of the contraction center were followed by imaging droplets over time for an hour.(a) Spinning disk confocal (top) and Bright-field (bottom) images from a time lapse movie (Video 3) of a droplet that starts in a centered state and breaks symmetry to become polar. (b) The symmetry breaking transition of droplets from a symmetric state to a polar state was characterized in 18 different droplets. The displacement of the aggregate from the center of the droplet is shown as a function of time for the different droplets. Time zero is defined as the onset of symmetry breaking for each droplet (see Materials and methods). (c-h) Analysis of the dynamics of aggregate position as a function of time in droplets in the centered state (c-e; N = 12) and during symmetry breaking (f-h; N = 18). (c,f) Tracks depicting the position of the aggregate in different droplets. (d,g) The mean squared displacement of aggregate positions as a function of time. The droplets in the centered state exhibit confined random fluctuations (d), whereas during symmetry breaking, the movement is directed (g). (e,h) The normalized velocity autocorrelation $c\left(\tau \right)=\frac{⟨\overrightarrow{V}\left(t\right)\cdot \overrightarrow{V}\left(t+\tau \right)⟩}{⟨\overrightarrow{V}\left(t\right)\cdot \overrightarrow{V}\left(t\right)⟩}$(mean ± STD; averaged over different droplets) is shown for the tracks on the left. The velocity autocorrelation (for t ≥ 0.5 min) is essentially zero in the centered state (e). During symmetry breaking, the aggregate velocity exhibits a positive correlation for time scales of up to ∼ 10 min (h).

Figure 2—figure supplement 1. Analysis of the dynamics of aggregate position as a function of time in droplets before symmetry breaking.

(a) The position of the aggregate in different droplets that eventually break symmetry was followed (as shown in Figure 2b). Tracks of the aggregates position are depicted during the initial period in which the aggregates remained nearly centered (i.e. for t < 0 in Figure 2b; N = 17). (b) The mean squared displacement of the aggregate position in different droplet is shown as a function of time. Thick gray line – mean MSD of droplets that remain centered for over an hour as shown in Figure 2d. The aggregates exhibit confined random fluctuations before breaking symmetry, similar to the dynamics of aggregates in centered droplets (Figure 2d). (c) The normalized velocity autocorrelation (mean ± STD; N = 17, averaged for the different droplets) is shown for the tracks on the left. The velocity is considerably less correlated over time than during the symmetry breaking phase (Figure 2h).