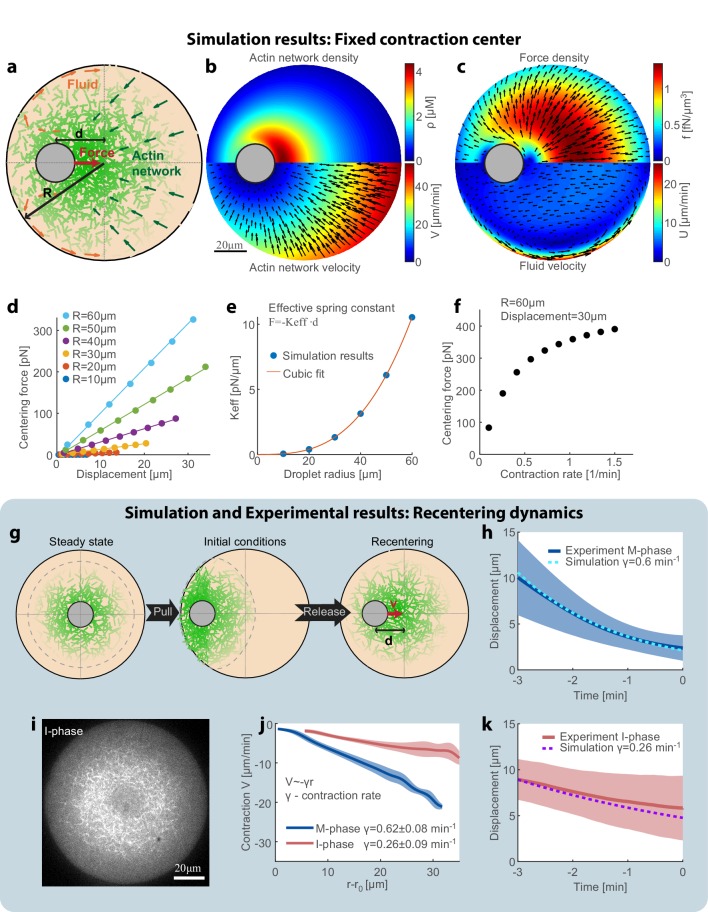
Figure 4. Recentering model: friction between the contracting network and the fluid cytosol generates a centering force.

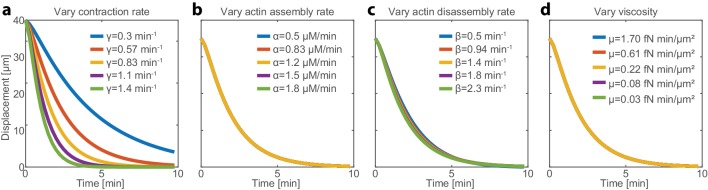
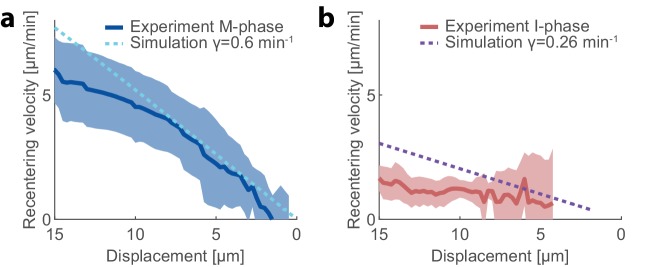
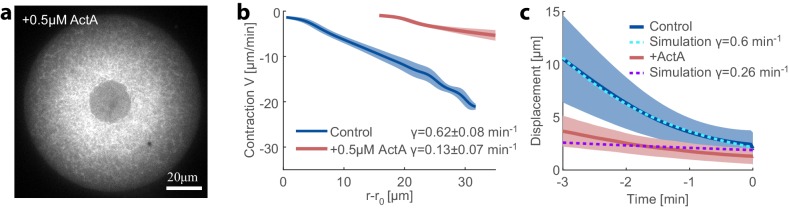
(a) Schematic illustration of the model. The system is modeled as a two-phase system composed of a contracting actin network and the surrounding fluid. (b–f) Simulation results of the model when the aggregate position is held fixed (Appendix 1). The simulation results for the steady-state actin network density and flow (b) and the surrounding fluid flow and force density (c) are shown. (d) The centering force is calculated from the simulation as the net force exerted on the aggregate as a function of the displacement from the droplet center at steady-state. The net centering force is plotted as a function of the displacement for droplets of different sizes (dots- simulations results; line- linear fit). (e) The effective spring constant of the centering force, determined from the slope of the linear fit to the simulation results in (d), is plotted as a function of the droplet radius (R). The effective spring constant increases as R³. (f) The centering force is plotted as a function of the network contraction rate. The centering for was calculated for a displacement of 30 µm in a droplet with a radius of R = 60 µm. The centering force increases with network contraction. (g–k) In the dynamic model (Appendix 1), the aggregate position is part of the dynamic variables of the system and moves according to the net force acting on it. (g) Schematic illustration of the dynamic model used to model the magnetic perturbation experiments. The initial conditions are obtained by displacing a centered steady-state configuration toward the side. Subsequently, the dynamics of the system lead to recentering of the aggregate. (h) The simulation results for the displacement of the aggregate as a function of time (dashed line) are compared to the average displacement determined experimentally in M-phase extracts (standard condition) (blue line; mean ± STD; Figure 3e). (i) Spinning-disk confocal image of the equatorial cross section of an I-phase extract droplet. The actin network is labeled with GFP-Lifeact. (j) Network contraction velocity measured as a function of distance from the inner network boundary, for M-phase and I-phase extracts (mean ± STD). The contraction rate, γ, is determined from the slopes of linear fits to the data (Malik-Garbi et al., 2019). (k) The simulation prediction for the displacement of the aggregate as a function of time (dashed line) are compared to the average displacement determined experimentally in I-phase extracts (red line; mean ± STD). The observed average I-phase contraction rate is used as an input for the simulation which contains no additional fit parameters.

Figure 4—figure supplement 1. The network contraction rate is the main control parameter for the hydrodynamic centering mechanism.

The sensitivity of the hydrodynamic centering mechanism to the characteristics of the actin meshwork and the fluid cytosol was evaluated by numerical simulations of the recentering dynamics, performed using different network and fluid parameters. (a-d) The simulation results for the contraction center displacement as a function of time following a magnetic perturbation are shown. The simulations were performed with the following parameter values R = 50 μm; α = 1 μM/min; β = 1.43 min⁻¹; γ = 0.67 min⁻¹; μ = 1.7 fN min/μm², except for the parameter varied in each graph as indicated. The network contraction rate is the main control parameter for the recentering mechanism. The recentering dynamics are considerably faster with higher network contraction rates (a), whereas the network assembly (c) and disassembly rates (d), and the fluid viscosity (b), have little influence on the recentering dynamics.

Figure 4—figure supplement 2. Aggregate recentering velocity in M-phase and I-phase extracts.

(a,b) The aggregate recentering velocity is depicted as a function of the displacement from the droplet center. The experimental results from magnetic pulling experiment are shown for (a) standard M-phase extracts (blue line; mean ± STD; Figures 3e and 4h) and (b) I-phase extracts (red line; mean ± STD; Figure 4k). The experimental data are compared to the results of simulations in M-phase or I-phase extracts (dashed lines), respectively. The observed contraction rates in M-phase and I-phase extracts (Figure 4j) are used as inputs for the respective simulations with no additional fit parameters.

Figure 4—figure supplement 3. Recentering dynamics in ActA-supplemented extract.

(a) Spinning-disk confocal image of the equatorial cross section in droplets supplemented with 0.5 μM ActA. The actin network is labeled with GFP-Lifeact. (b) Network contraction velocity measured as a function of distance from the inner network boundary, for control and ActA supplemented extracts (mean ± STD). The contraction rate, γ, is determined from the slopes of linear fits to the data (c) The simulation predictions for the displacement of the aggregate as a function of time (dashed lines) are compared to the average displacement determined experimentally in control and ActA supplemented extracts (solid line; mean ± STD).

Figure 4—figure supplement 4. Cell-cycle dependence of the localization of the contraction center.

The localization pattern in I-phase extract, which exhibits weak contraction (Field et al., 2011), is characterized by less centered droplets and more symmetry breaking compared to M-phase extract. The position of the aggregate surrounding the contraction center was determined for a population of droplets formed with M-phase extract (left) or I-phase extract (right). The displacement of the aggregate from the center is plotted as a function of droplet radius. The colored regions depict the different size ranges: small droplets that are primarily polar (red), intermediate range with both polar and symmetric droplets (yellow), and large droplets which are mostly centered (green). The dashed black line marks the droplet radius, and the dashed red line marks the displacement where the aggregate reaches the boundary (droplet radius minus aggregate radius). I-phase droplets are more likely to be polar, even at large droplet sizes that remain centered in M-phase.