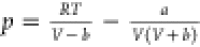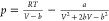Table 1. PVT Relations and α-Functions of Cubic EoSs Evaluated in this Study.

CEOS	PVT relation	α-function	model features
SRK29		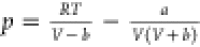α(Tr) = [1 + (0.480 + 1.574 ω – 0.176 ω2)·(1 – Tr0.5)]2	the accuracy of SRK EoS was significantly improved from RK in vapor pressure prediction.
SRK–Twu18		α(Tr) = α(0)(Tr) + ω(α(1)(Tr) – α(0)(Tr))	α of attractive term is a linear function of the acentric factor, which can be easily extrapolated to the high-pressure region. This model ensured more reliable and precise calculation results of the high-pressure region for heavy hydrocarbons.
		α(i)(Tr) = TrN(i)(M(i) – 1)eL(i)(1 – TrN(i)(M(i))a For
PR30		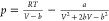α(Tr) = [1 + (0.37464 + 1.54226 ω – 0.26992 ω2)·(1 – Tr0.5)]2	the PR EoS had comparable accuracy of SRK EoS in vapor pressure prediction and performed much better in liquid density calculation.
PRSV31		α(Tr) = [1 + m(1 – Tr0.5)]2	this model proposed an additional parameter for every pure substance and can yield a good agreement with equilibrium data.
		m = k0 + k1(1 +Tr0.5)(0.7 – Tr)b For
		k0 = 0.378893 + 1.4897153 ω – 0.17131848 ω2 + 0.0196544 ω3
TST32		α(Tr) = α(0) (Tr) + ω(α(1)(Tr) – α(0)(Tr))	the PVT relation of Twu–Sim–Tassone (TST) was slightly different from PR or SRK. This EoS has been found to have better prediction of vapor pressure as well as liquid densities from the triple point to the critical point.
		α(i) (Tr) = TrN(i)(M(i) – 1)eL(i)(1 – TrN(i)(M(i))c

^{a For}parameters L, M, and N for the SRK–Twu model, please refer to Table S9 of the Supporting Information.

^{b For}parameter k₁, please refer to Table S8 of the Supporting Information.

^cFor parameters L, M, and N for TST EoS, please refer to Table S9 of the Supporting Information.