Abstract
The Wenzel model, commonly used for predicting the equilibrium contact angle (CA) of drops which penetrate the asperities of a rough surface, does not account for the liquid volume stored in the asperities. Interestingly, many previous experimental and molecular dynamics studies have noted discrepancies between observed CAs and those predicted by the Wenzel model because of this neglected liquid volume. Here, we apply a thermodynamic model to wetting of periodically patterned surfaces to derive a volume-corrected Wenzel equation in the limit of small pattern wavelength (compared to drop size). We show that the corrected equilibrium CA is smaller than that predicted by the Wenzel equation and that the reduction in CA can be significant when the liquid volume within the asperities becomes non-negligible compared to the total droplet volume. In such cases, the corrected CAs agree reasonably well with experimental observations and results of molecular dynamics simulations reported in previous studies.
1. Introduction
In predicting the wetting characteristics of physically patterned surfaces, two models are commonly used. One is the Cassie model,1 in which a droplet is assumed to remain suspended above the asperities in the surface, thereby resting on a composite bed of air and solid. In this case, the predicted equilibrium contact angle (CA) of the droplet, θC, is given by the Cassie equation
| 1 |
where fs is the solid fraction, defined as the fraction of the basal area of the drop characterized by the solid–liquid contact, and θe is the intrinsic CA, or Young’s angle,2 for a perfectly smooth solid surface. The other commonly used model is the Wenzel model,3 which assumes that the droplet penetrates the asperities in the surface. The equilibrium CA in this case, θW, is given by the Wenzel equation
| 2 |
where r is the roughness factor, defined as the ratio of the actual surface area to that projected in a plane parallel to the nominal surface (r ≥ 1 by definition).
Although these models are often used to describe wetting, reports of discrepancies between the model predictions and observed CAs are common.4−8 Such disagreements have stirred much debate over the years as to the applicability of the Cassie and Wenzel models, resulting in the general consensus that such models apply only in the limit of surface features much smaller than the drop size, while outside of this limit, contact line pinning and other effects become important.9−17
The Wenzel equation was originally derived intuitively by considering the roughness of a surface as amplifying the effective solid–liquid and solid–vapor interfacial free energies by the roughness factor.3 The derivation of the Wenzel equation implicitly assumes that the volume of the liquid stored within the asperities under the droplet is negligible and therefore has no effect on the CA. Presumably, the liquid removed from the droplet cap to fill the asperities under the droplet base should have an effect on the CA—namely, it should lead to smaller CAs than those predicted by the Wenzel equation.
Although there has been some previous work to understand higher-order effects on the Wenzel prediction, these studies have focused mainly on microscopic effects related to molecular interactions18−20 or contact line pinning.8 To our knowledge, there have been no previous studies to address the role of the non-negligible liquid volume stored in the surface asperities in a general way. Here, we tackle the problem of modifying the Wenzel equation to more accurately predict the equilibrium CA on surfaces for which the asperity volume is large enough to have an observable effect on the CA. We apply perturbation theory to derive the first-order correction to the Wenzel prediction, and we provide an intuitive interpretation for the correction in the two-dimensional case and explain why this intuition breaks down in the three-dimensional case. Finally, we compare our results with numerical predictions of the static CA on physically patterned surfaces and with experimental observations and results of molecular dynamics (MD) simulations.
2. Results and Discussion
2.1. Two-Dimensional Model
2.1.1. Formulation
Using Young’s equation,2 the difference in the free energy of a drop on a solid surface, relative to the same drop in air, may be written as
| 3 |
where σlv is the liquid–vapor interfacial energy per unit area, Asl and Alv denote the solid–liquid and liquid–vapor interfacial areas, respectively, and Ug represents the gravitational potential energy. To simplify the problem, we initially consider two-dimensional (cylindrical cap) drops on two-dimensional surface patterns. In this case, E and A can be interpreted as free energy and area, respectively, per unit length along the axis of the cylindrical droplet. Making all lengths dimensionless with the radius a of the cylindrical droplet before it comes into contact with the surface and making the energy per unit length dimensionless with σlva, the dimensionless expression for the free energy becomes
| 4 |
where the overbars denote dimensionless quantities. In what follows, we will drop the overbars and all quantities will be understood to be dimensionless unless otherwise stated. Furthermore, we will focus on the small drop regime in which the gravitational potential energy contribution is negligible and the drop profile assumes a circular cap shape.
For a drop in the Wenzel mode on a surface with an arbitrary periodic roughness pattern, we can find expressions for Asl and Alv in terms of the asperity volume and the total solid–liquid interfacial length over one wavelength of the roughness pattern. Specifically, for a circular cap drop profile with radius of curvature R
| 5 |
where θ is the apparent CA of the droplet, s is the total solid–liquid interfacial area (per unit length along the axis of the cylindrical drop) contained in one wavelength of the roughness pattern, and n is the number of asperities spanned by the base of the drop. For roughness patterns with a very small wavelength λ, relative to the drop size, the value of n may be approximated by
| 6 |
Using eq 5 to substitute for Alv and Asl in eq 4, and recognizing s/λ as the roughness factor r appearing in the Wenzel equation, yields
| 7 |
for the dimensionless free energy of a two-dimensional drop in the Wenzel mode.
Upon making contact with the surface, some liquid from the droplet will be stored in the asperities of the patterned surface. Conservation of the mass of the liquid requires
| 8 |
where Va is the volume of the liquid (per unit length along the droplet axis) stored within a single asperity and the right-hand side (RHS) represents the dimensionless drop volume (per unit length along the axis of the cylindrical drop) before contact with the solid substrate. Using approximation 6 for n, eq 8 can be rewritten as
| 9 |
where h ≡ Va/λ may be thought of as a dimensionless average asperity depth. We note that eq 9 is quadratic in R and therefore may be easily solved to obtain an expression for R in terms of θ. With the resulting expression for R(θ), the equilibrium CA for a drop in the Wenzel mode can be determined by minimizing the free energy expression in eq 7 with respect to the CA θ. Because the resulting expression cannot be solved explicitly for θ, we will use perturbation analysis to find an analytical expression for the equilibrium CA in the small-h limit.
2.1.2. Perturbation Analysis
Differentiating eqs 7 and 9 with
respect to θ and requiring 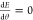 at equilibrium yields an equation of the
form
at equilibrium yields an equation of the
form
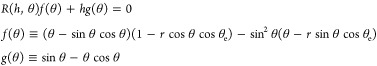 |
10 |
for the equilibrium CA θ(h), where R(h,θ) emphasizes the fact that the radius of curvature has both explicit h dependence and implicit h dependence through θ (as is evident from the solution to eq 9). The expression for f can be simplified to
| 11 |
Noting that g(θ) > 0 for 0 < θ ≤ π, we can rewrite eq 10 as
| 12 |
For small values of h, regular perturbation expansions of the form
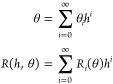 |
13 |
can be used in conjunction with domain perturbations
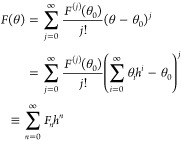 |
14 |
for F ∈ {R,k} in eq 12 to determine the corrections to the CA at various orders in h. In eq 14, F(j) denotes the j-th derivative of F(θ) with respect to θ and Fn stands for the collection of all O(hn) terms in the full perturbation expansion of F(θ).
Recognizing that
| 15 |
by setting h = 0 in eq 9, the O(1) contribution to eq 12 yields
| 16 |
which has the solution
| 17 |
corresponding to the original Wenzel model. At O(h), eq 12 simplifies to
| 18 |
Noting k0 = 0 from eq 16 and using the definition for k(θ) from eq 12 results in
| 19 |
as the leading-order correction to the Wenzel CA. Continuing through O(h3) leads to the following expression for the volume-corrected Wenzel CA, θW*, for a two-dimensional droplet
| 20 |
where R0 is given by 15. Using the expansion of θW* in eq 12, we may similarly express R as a power series in h to find
| 21 |
Interestingly, the O(h) correction to the interface curvature vanishes.
Finally, we use eq 20 to obtain the extended Wenzel equation
| 22 |
which constitutes one of the central results of this study. We note that the O(h2) correction to cos θW* vanishes and the leading-order correction is positive, which causes a reduction in the Wenzel CA. Higher-order corrections can be easily calculated using the Sage notebook21 provided in the Supporting Information.
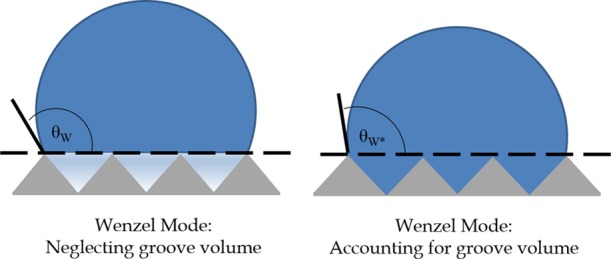
A simple physical interpretation for the O(h) correction to the CA in the Wenzel model can be provided by first considering a drop for which the liquid volume stored in the asperities under the drop has been neglected, as shown in Figure 1A. This corresponds to the prediction of the original Wenzel model, wherein the drop can be viewed as resting on a smooth flat surface (because the asperity volume has been neglected) with solid–liquid and solid–vapor interfacial energies amplified by the roughness factor. To account for the liquid volume stored in the asperities, consider the surface pattern to consist of one long asperity of depth h = Va/λ (i.e., with the volume equivalent to the total volume of the n asperities present on the patterned surface) extending across the base of the droplet, instead of consisting of individual asperities. The stored liquid volume can then be accounted for by shifting the droplet toward the substrate by a distance h while maintaining a constant radius of curvature, R0, as suggested by eq 22 rewritten as
| 23 |
to O(h2). This causes the CA to decrease to the corrected value, θW*, as shown in Figure 1B. Hence, the corrected CA can simply be viewed as the CA one would obtain by removing a layer of thickness h from the base of the drop to account for the volume stored in the asperities.
Figure 1.
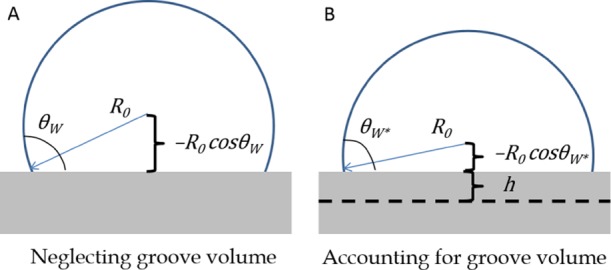
(A) Droplet in the Wenzel model for which the liquid volume in the asperities has been neglected. (B) Same droplet in the Wenzel mode, now accounting for the liquid volume in the asperities. The circular cap profile of the fixed radius of curvature is shifted toward the substrate by the average asperity depth h, thereby causing a reduction in CA, as visible in the sketch.
2.2. Three-Dimensional Model
2.2.1. Formulation
In the three-dimensional case, we again start with the expression for the dimensionless free energy of the droplet given by eq 4, where the expression is now made dimensionless with a2σlv and a is the spherical equivalent radius—that is, the radius of the spherical droplet before it comes into contact with the surface. Assuming a spherical cap shape for the droplet (which is again a valid assumption for negligible gravitational effects), we can write the dimensionless liquid–vapor and solid–liquid interfacial areas as
| 24 |
respectively, where R is the radius of curvature of the spherical cap and s now represents the total solid–liquid interfacial area per unit cell of the physical pattern. Again assuming that the drop is large relative to the surface features, we may approximate n as
| 25 |
where Aa represents the projected area of a unit cell in a plane parallel to the nominal surface. Substituting for Alv and Asl in eq 4 and recognizing s/Aa as the roughness factor r, we can write the dimensionless free energy of a three-dimensional droplet in the Wenzel model as
| 26 |
The constant volume condition may now be written as
| 27 |
where Va is the liquid volume stored in a single asperity and the RHS represents the dimensionless drop volume before coming into contact with the substrate. Using the approximation for n given by eq 25, this expression can be rewritten as
| 28 |
where h ≡ Va/Aa is again defined as a dimensionless average asperity depth. Although eq 28 could be solved analytically for R, the resulting expression is rather unwieldy and it will not be possible to obtain an explicit expression for the equilibrium CA via minimization of the free energy expression 26. Therefore, we will again use perturbation analysis to obtain an analytic expression for the equilibrium CA in the small-h limit.
2.2.2. Perturbation Analysis
For the three-dimensional
model, we follow the same procedure outlined earlier for the two-dimensional
case. Differentiating eqs 26 and 28 with respect to θ and
requiring 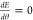 at equilibrium yields
at equilibrium yields
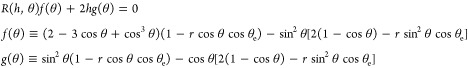 |
29 |
where R(h,θ) is given by eq 28. These expressions for f and g can be simplified to
| 30 |
which allows us to rewrite eq 29 as
| 31 |
We note that the factor of two in the second term of eq 31 was not present in the corresponding equation for the two-dimensional model (eq 12). Using perturbation expansions of the form given by eqs 13 and 14, we find the corrections to the Wenzel CA and radius of curvature of the drop to be
| 32 |
and
| 33 |
respectively, where
| 34 |
and once again
| 35 |
corresponding to the original Wenzel model. The extended Wenzel equation is thus given by
| 36 |
which represents another one of the central results of this study.
Here, we note again the factor of two appearing in the O(h) terms of eqs 32 and 36, which was not present in the corresponding expressions for the two-dimensional model given by eqs 20 and 22. This factor of two arises because of the appearance of an O(h) correction to the three-dimensional radius of curvature given by eq 33, in contrast to the O(h2) correction reported earlier for the two-dimensional model (eq 21). Essentially, in the three-dimensional model, an O(h) reduction in the CA occurs with a concomitant O(h) increase in the radius of curvature. As a result, the simple intuitive interpretation of the CA correction presented earlier for the two-dimensional model, which assumed a constant radius of curvature to O(h), does not hold in the three-dimensional model.
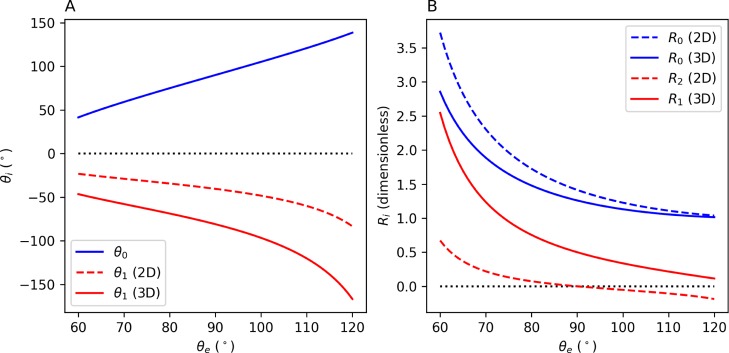
Figure 2 shows the first-order correction terms for the CA and radius of curvature as a function of intrinsic CA for a surface with the fixed roughness factor r = 1.5. The upper limit of θe ≈ 120° in this figure corresponds to the largest θe for known materials,22−25 while the lower limit of θe = 60° was set to probe a region of parameter space symmetric about θe = 90°. The leading-order CA term, θ0, in Figure 2A is the CA predicted by the original Wenzel model, for which it is well known that the surface roughness simply amplifies the intrinsic hydrophobicity or hydrophilicity of the surface. For the first-order correction to the CA (Figure 2A), we note that θ1 < 0 in both the 2D and 3D cases, causing the primary reduction in CA because of the volume correction in the extended Wenzel model. It is important to note that values of θ1 in this figure must be multiplied by the small dimensionless average asperity depth, h, to yield the correction to the CA. As shown in Figure 2B, the leading-order term for the radius of curvature, R0, is always greater than 1 for both 2D and 3D cases, which ensures that the first-order corrections to the CA in eqs 22 and 36 remain small (for small h). The first-order correction to the radius of curvature is always positive for the 3D case, indicating that drops become more flattened regardless of the intrinsic hydrophobicity or hydrophilicity of the surface. In the 2D case, on the other hand, R1 = 0 and the first non-zero correction to the radius of curvature, R2, is positive for θe < 90° and negative for θe > 90°, indicating that drops become less (more) flattened on intrinsically hydrophobic (hydrophilic) surfaces.
Figure 2.
Leading-order approximation and first non-zero correction terms for (A) CA and (B) radius of curvature of 2D and 3D droplets as a function of intrinsic CA, θe, for fixed roughness factor r = 1.5. For the 2D case, the first-order correction to the radius of curvature vanishes (R1 = 0). The dotted lines at θi = 0 and Ri = 0 are drawn to guide the eye.
2.3. Comparison with the Wenzel Model on Simple Surface Patterns
In this section, we explore and test the predictions of the extended Wenzel model on various physically patterned surfaces. For all surfaces considered below, we will set θe = 115°.
2.3.1. Two-Dimensional Rectangular Patterns
We first compare the predictions of the extended Wenzel model with those of the original Wenzel model by considering patterned surfaces with rectangular grooves of the form shown in Figure 3. Specifically, we consider self-similar surfaces with a fixed aspect ratio of H/W = 1.5. For such surfaces, the roughness factor may be written as
| 37 |
and the average groove depth may be written as
| 38 |
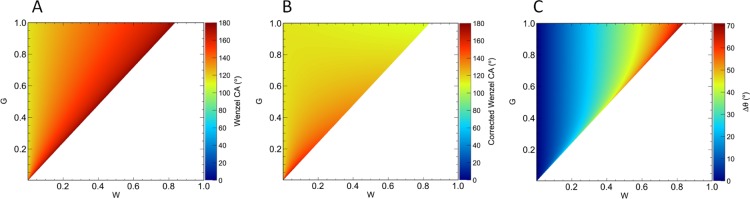
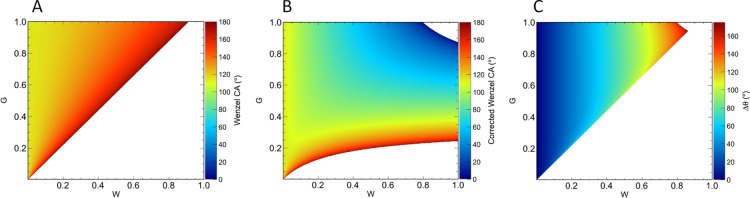
where α ≡ G/W. Substituting these expressions into eq 22, we can compute the CAs predicted by the extended and original Wenzel equations. The results are shown in Figure 4. We note significant differences in the CAs predicted by the two models for large surface features, with the differences becoming smaller for smaller surface feature sizes, as expected. The white region in the figure lies outside the domain of the Wenzel model given by r|cos θe| ≤ 1 which, for θe = 115°, holds when r ≲ 2.366.
Figure 3.
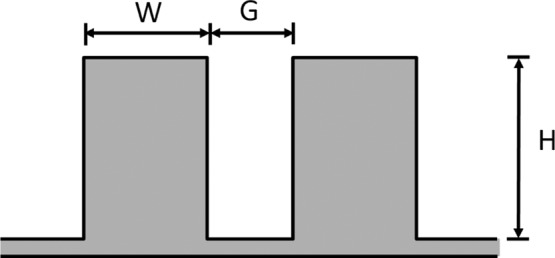
Two-dimensional periodic surface pattern consisting of rectangular grooves of width G, spacing W, and height H.
Figure 4.
Phase diagrams of the CA as a function of groove width, G, and groove spacing, W. The aspect ratio was fixed at H/W = 1.5. (A) CA predicted by the original Wenzel equation, θW. (B) CA predicted by the extended Wenzel model, θW*. (C) Difference between the predictions of the two models (θW – θW*). The white regions lie outside the domain of the Wenzel equation.
Figure 4C shows the difference between the CAs shown in Figure 4A,B. We note that the difference is positive everywhere because accounting for the liquid volume stored in the asperities causes a reduction in the predicted θW*.
2.3.2. Two-Dimensional Triangular Patterns
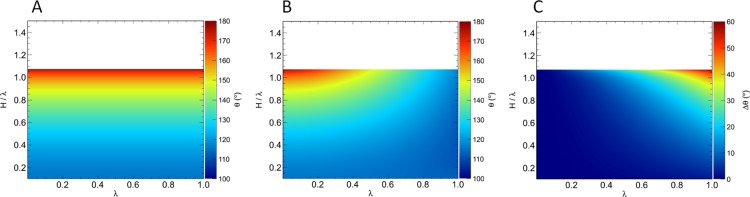
We next consider surface patterns consisting of periodic isosceles triangular grooves, such as the one illustrated in Figure 5. Such surfaces are fully specified by wavelength λ and height H. The roughness factor r and asperity volume Va for such surfaces are given by
| 39 |
which leads to an average
groove depth of 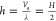 . The CAs predicted by the original and
extended Wenzel models using these values are shown in Figure 6A,B, respectively. In Figure 6A, we see that the
predictions of the original Wenzel model are independent of λ
and depend only on H/λ, which appears in the
expression for the roughness factor (eq 39). In Figure 6B, on the other hand, we observe an effect of λ
on the CA of the droplet, in addition to the effect of H/λ, namely, increasing λ causes a reduction in the CA
because of the larger volume of the asperities.
. The CAs predicted by the original and
extended Wenzel models using these values are shown in Figure 6A,B, respectively. In Figure 6A, we see that the
predictions of the original Wenzel model are independent of λ
and depend only on H/λ, which appears in the
expression for the roughness factor (eq 39). In Figure 6B, on the other hand, we observe an effect of λ
on the CA of the droplet, in addition to the effect of H/λ, namely, increasing λ causes a reduction in the CA
because of the larger volume of the asperities.
Figure 5.

Periodic surface pattern consisting of isosceles triangular asperities defined by wavelength λ and height H.
Figure 6.
(A) CA predicted by the original Wenzel equation, θW, for the triangular surface pattern as a function of wavelength, λ, and structure aspect ratio, H/λ. (B) CA predicted by the extended Wenzel model, θW*, as a function of λ and H/λ. (C) θW – θW* for the patterned surface. The white regions lie outside the domain of the Wenzel equation.
Figure 6C shows the difference in CAs predicted by the original and extended Wenzel models for the triangular grooved surface. Clearly, the correction term in the extended Wenzel model is negligible for very small surface features but can cause a significant change in the predicted CA for larger feature sizes. We again note that the difference in the CA is positive, indicating that by not accounting for the liquid volume stored in the asperities under the droplet, the original Wenzel model overestimates the CA.
2.3.3. General Two-Dimensional Surface Patterns
Finally, we consider two-dimensional surfaces with general periodic patterns that can be characterized by roughness factor r and average groove depth h, where h is the asperity volume per wavelength of the roughness pattern, as defined earlier. Figure 7A shows the predictions of the original Wenzel model (eq 2) for such a surface as a function of r and h. Clearly, the predictions of the original Wenzel model are a function of r only.
Figure 7.
(A) CA predicted by the original Wenzel equation, θW, on a general two-dimensional surface pattern characterized by roughness factor r and average asperity depth h, where h is defined as the volume of an asperity divided by the wavelength of the roughness pattern. (B) CA predicted by the extended Wenzel model, θW*, as a function of r and h. (C) θW – θW* for a general surface pattern. The white regions lie outside the domain of the Wenzel equation. The maximum r for which the Wenzel equation is defined depends on θe.
The corresponding predictions based on the extended Wenzel model are presented in Figure 7B, where we observe a significant effect of h on the predicted CAs, in addition to the effect of r. In Figure 7C, we plot the difference between the predictions of the original Wenzel model and those of the extended Wenzel model on the same patterned surfaces. Here, we see that for patterned surfaces with h > 0.1, significant discrepancies in the CAs predicted by the two models arise with increasing r. For h = 0.3, discrepancies as large as about 40° may occur, indicating that for such surfaces, the liquid volume stored in the asperities is very important in determining the CA of the droplet.
2.3.4. Three-Dimensional Surface Patterns
To explore predictions of the three-dimensional model, we consider a three-dimensional surface pattern like the one shown in Figure 8, consisting of W × W square prisms of height H, separated by groove width G, and with unit cell area (G + W)2. Specifically, we consider self-similar surfaces for which H/W = 1.5 and θe = 115°, as in the case of the two-dimensional rectangular pattern. For such surfaces, the roughness factor and the average groove depth may be written as
| 40 |
and
| 41 |
respectively, where again α ≡ G/W.
Figure 8.
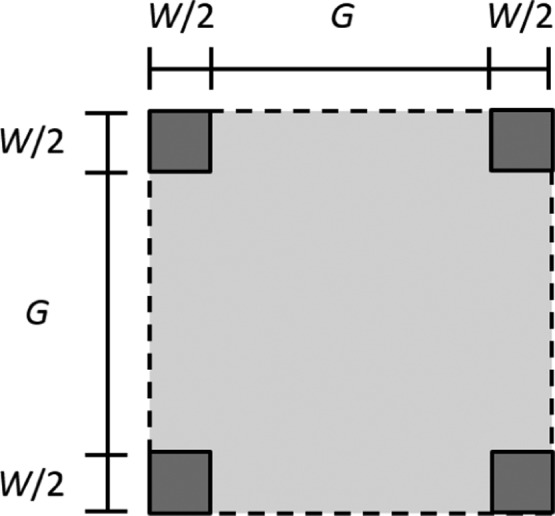
Top-down view of a unit cell for the three-dimensional surface pattern consisting of W × W right square prisms of height H separated by groove width G, with unit cell area (G + W)2.
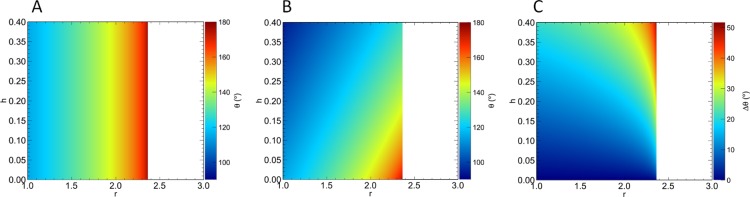
The predictions of the original Wenzel model for such surfaces are shown in Figure 9A. We note that here the predicted CA depends only on α (the ratio of G/W), as expected from the dependence of r on α in eq 40. The predictions of the extended Wenzel model are shown in Figure 9B. Interestingly, the domain of applicability of the extended Wenzel model has expanded significantly over the region of phase space represented in the diagram, whereas a similar effect was not observed for the two-dimensional model presented earlier. This difference arises from the dependence of the corrected CA on the leading-order radius of curvature R0 (which is obtained by setting h = 0 in eqs 9 and 28 in the two cases) via eqs 22 and 36. In the two-dimensional model, the value of R0 depends on θ0 = arccos(r cos θe), which becomes undefined when |r cos θe| > 1. In contrast, the three-dimensional model, for which R0 does not depend on θ0 (but, rather, depends on cos θ0), does not suffer from this limitation, thereby having an expanded region of validity. The difference between the predictions of the original and extended Wenzel models is shown in Figure 9C over the region of parameter space where both predictions are defined. It is clear that the correction to the Wenzel CA is significant over most of this region.
Figure 9.
Predictions for a three-dimensional self-similar surface pattern like the one depicted in Figure 8, with H/W = 1.5. (A) Predictions of the original Wenzel model. (B) Predictions of the extended Wenzel model to O(h). (C) Difference in the predictions of (A,B) (original Wenzel CA minus corrected Wenzel CA). The white regions lie outside the domains of one or both of the models.
2.4. Comparison to a Thermodynamic Model with Contact Line Pinning
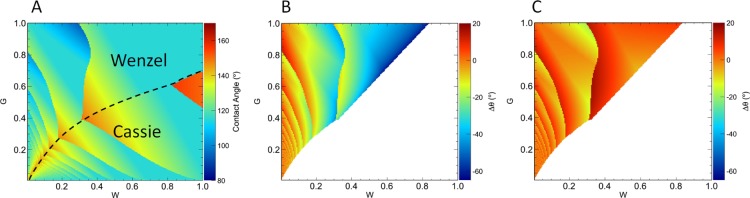
In Figure 10, we revisit the two-dimensional rectangular patterns to compare the asymptotic predictions of the extended Wenzel model (and those of the original Wenzel model) with numerical predictions of a computational thermodynamic model for the two-dimensional rectangular patterned surface described above. Details of the computational model have been described elsewhere.16,26,27 Briefly, the computational model involves placing a drop on the surface shown in Figure 3 and then performing a systematic search for the global minimum free energy configuration of the drop in terms of the wetting mode (Cassie or Wenzel) and the number of grooves spanned or filled by the drop and accounting for pinning effects at the three-phase contact line—effects that are not included in the original or extended Wenzel models. We note that in the small-drop limit considered here, where the effects of gravity are negligible, the predictions of the thermodynamic model are in agreement with molecular dynamics simulations.28
Figure 10.
Phase diagrams of the CA as a function of groove width, G, and groove spacing, W. The aspect ratio was fixed at H/W = 1.5. (A) Predictions for CA given by a computational model described elsewhere.26,27 (B) CA predicted by the computational model minus that predicted by the original Wenzel model. (C) CA predicted by the computational model minus that predicted by the extended Wenzel model. In both B and C, only the regions in which the computational model predicts a Wenzel equilibrium configuration are considered. The white areas either represent a Cassie equilibrium configuration or regions that lie outside the domain of the Wenzel equations.
Figure 10A shows the predictions of the computational thermodynamic model, with the dashed curve marking the division between regions of phase space in which the Wenzel model is preferred and those in which the Cassie model is preferred. Figure 10B shows the difference between the CAs predicted by the original Wenzel model and those predicted by the computational model in the region of phase space that lies within the domain of the Wenzel equation and for which the computational model predicts droplets in the Wenzel mode. Figure 10C shows the difference between CAs predicted by the extended Wenzel model and those predicted by the computational model. Here, we see that the differences become notably smaller when using the extended Wenzel model. The differences that remain between the extended Wenzel model and the computational model are primarily due to pinning effects arising from the finite size of the surface features being scanned over in the phase diagram, which are accounted for in the computational model but not in the extended Wenzel model. Despite the fact that the extended Wenzel equation was derived for the limit in which surface features are much smaller than the drop size (and hence does not account for pinning effects), the extended equation provides surprisingly good predictions for large surface features.
2.5. Comparison with Experiments
To validate the three-dimensional extended Wenzel model, we compare its predictions with experimental results reported by Barbieri et al.29 for the static CAs of droplets on periodic three-dimensional surface patterns consisting of various arrangements (hexagonal, square, and honeycomb) of cylindrical pillars. The surfaces are characterized by pitch p (representing the minimum spacing between surface features), disposition factor A (denoting the statistical number of pillars in area p2), diameter d, and height H. The disposition factor A depends on the geometrical arrangement, A = 0.770, 1, or 1.547 for the honeycomb, square, and hexagonal arrangements, respectively. In terms of these parameters, we can express the roughness factor and average asperity depth as
| 42 |
and
| 43 |
respectively. The 3 μL drops used in the experiments correspond to a spherical equivalent radius of a ≈ 895 μm.
We compare the predictions of the extended Wenzel model with the CA measurements reported by Barbieri et al.,29 as shown in their Figure 6A, for a system with θe = 110° and surface patterns characterized by d = 10 μm, H = 40 μm, and various pitch values. The resulting comparison is presented in Table 1. To make a valid comparison, we have restricted attention to surfaces with pitch values of p ≥ 100 μm, for which droplets were considered to be in the Wenzel wetting mode. Also, we note that for these surfaces, the feature sizes were sufficiently smaller than the drop size (namely, d/a = 0.011, H/a = 0.045, and 0.11 ≤ p/a ≤ 0.17) such that the Wenzel model may be reasonably expected to apply.
Table 1. Comparison of the Extended and Original Wenzel Model Predictions with Experimental Observations by Barbieri et al.29.
| arrangementa | Ab | pitch (μm)c | rd | hd | θobs (deg)e | θW (deg)f | θW* (deg)g |
|---|---|---|---|---|---|---|---|
| honeycomb | 0.770 | 100 | 1.10 | 0.0444 | 109 | 112 | 107 |
| 150 | 1.04 | 0.0446 | 106 | 111 | 106 | ||
| square | 1 | 110 | 1.10 | 0.0444 | 104 | 112 | 108 |
| 120 | 1.09 | 0.0444 | 102 | 112 | 107 | ||
| 150 | 1.06 | 0.0445 | 109 | 111 | 107 | ||
| hexagonal | 1.547 | 120 | 1.14 | 0.0443 | 110 | 113 | 108 |
| 150 | 1.09 | 0.0445 | 113 | 112 | 107 |
Represents the arrangement of cylindrical pillars on the surface.
The disposition factor A represents the statistical number of pillars per unit area.
The pitch p represents the smallest center-to-center pillar spacing for a particular surface pattern.
The roughness factor r and the average asperity depth h were calculated from eqs 42 and 43, respectively, for d = 10 μm and H = 40 μm. h was made dimensionless with a spherical equivalent radius of a = 895 μm.
The experimentally observed CA.
The original Wenzel prediction.
The extended Wenzel prediction.
As described by Barbieri et al., each of the observed CAs (θobs) reported in Table 1 corresponds to the average of at least six static CA measurements made on the two sides of at least three drop profiles at different locations on the substrate. In addition, all measured CAs were reported to lie within ±3° of the mean. From the data in Table 1, we note that for all but one CA measurement, the observed CA was overpredicted by the original Wenzel model. In most cases, the CA predicted by the corrected Wenzel model was closer to the experimentally observed value, which seems to indicate that the asperity volume had an effect on the observed CA consistent with the correction suggested by the extended Wenzel model. Despite the agreement of our model with the experiment, we note that there are examples of other experiments for which our model does not agree with the observed CAs. Presumably, this is due to the limited region of parameter space for which our model applies—namely, small wavelength roughness with a non-negligible asperity volume. In some studies, for example, the h factor is much too small (h ≲ 0.005) for our model to predict a significant difference in CA from that predicted by the original Wenzel model.30−36 In such cases, the observed discrepancies between observed CAs of droplets in the Wenzel mode and those predicted by the Wenzel model might be related to pinning effects at the three-phase contact line, causing the measured static CA to differ from the most stable CA,37 as neither the Wenzel model nor our correction accounts for pinning.8
2.6. Comparison with Molecular Dynamics Simulations
Molecular dynamics simulations have proven extremely useful in the study of wetting phenomena for probing regions of parameter space that are difficult to explore experimentally.28,38,39 Multiple studies have noted discrepancies between results of MD simulations and the predictions of the Wenzel model,40−44 presumably because of the fact that the MD drops are often similar in size to the surface features, in which case both contact line pinning and the volume of the liquid stored in the asperities become important. Here, we compare the predictions of our volume-corrected Wenzel model with the results of an MD study of wetting by Hirvi and Pakkanen,40 in which the authors observed CAs smaller than those predicted by the Wenzel model. In the study, the authors simulated the wetting of one-dimensional nanogrooved polyethylene (PE) and poly(vinyl chloride) (PVC) surfaces of various dimensions by nanodroplets of two different sizes, with surfaces characterized by step width ay, groove width by, and step height H, as described in Table 1 of their paper. The simulated droplets consisted of either 4000 or 13,500 molecules, which we refer to as small and large droplets, having radii of 30.6 and 45.8 Å, respectively.
In Table 2, we compare the observed CAs from the MD simulations (as reported in Tables 4 and 5 of their paper)40 with the CAs predicted by both the standard and the first-order-corrected Wenzel equation. Although the authors measured two CAs for each simulated droplet, with one measured in a plane parallel to the grooves and the other measured perpendicular to the grooves, we compare only with those measured perpendicular to the grooves. We note that in all but one case, θsim < θW and in many cases, θW* is closer to θsim than is θW because of the liquid volume stored in the asperities under the droplet.
Table 2. Comparison of the Extended and Original Wenzel Model Predictions with Molecular Dynamics Simulations by Hirvi and Pakkanen.40.
| materiala | drop sizeb | θec | ayd | bye | Hf | rg | hh | θsimi | θWj | θW*k |
|---|---|---|---|---|---|---|---|---|---|---|
| PE | small | 115.2 | 5.06 | 4.80 | 3.69 | 1.75 | 0.0588 | 118.8 | 138.1 | 129.0 |
| 9.99 | 9.73 | 3.69 | 1.37 | 0.0596 | 112.0 | 125.8 | 118.1 | |||
| 9.99 | 9.73 | 7.39 | 1.75 | 0.119 | 128.6 | 138.2 | 120.7 | |||
| large | 114.4 | 5.06 | 4.80 | 3.69 | 1.75 | 0.0392 | 118.7 | 136.2 | 130.2 | |
| 9.99 | 9.73 | 3.69 | 1.37 | 0.0397 | 119.0 | 124.6 | 119.4 | |||
| 9.99 | 9.73 | 7.39 | 1.75 | 0.0795 | 132.5 | 136.3 | 124.5 | |||
| PVC | small | 95.6 | 5.38 | 5.10 | 5.12 | 1.98 | 0.0815 | 88.5 | 101.1 | 93.0 |
| 10.62 | 10.34 | 5.12 | 1.49 | 0.0826 | 91.9 | 98.4 | 90.3 | |||
| 12.02 | 8.94 | 10.24 | 1.98 | 0.143 | 107.6 | 101.1 | 86.9 | |||
| 17.26 | 3.70 | 30.72 | 3.93 | 0.177 | 92.7 | 112.6 | 93.3 | |||
| 12.02 | 8.94 | 30.72 | 3.93 | 0.429 | 0 | 112.6 | 66.2 | |||
| large | 92.6 | 5.38 | 5.10 | 5.12 | 1.98 | 0.0543 | 88.7 | 95.1 | 90.0 | |
| 10.62 | 10.34 | 5.12 | 1.49 | 0.0551 | 90.3 | 93.9 | 88.7 | |||
| 12.02 | 8.94 | 10.24 | 1.98 | 0.0953 | 99.7 | 95.1 | 86.1 | |||
| 12.02 | 8.94 | 30.72 | 3.93 | 0.286 | 88.0 | 100.3 | 71.8 |
The material used to construct the substrate (PE = polyethylene, corresponding to Table 4 in ref (40), and PVC = poly(vinyl chloride), corresponding to Table 5 in ref (40)).
Small drops consisted of 4000 molecules and large drops consisted of 13,500 molecules, corresponding to spherical equivalent radii of a = 30:6 Å and a = 45:8 Å, respectively.
All angles in the table are reported in degrees.
Step width in Å.
Groove width in Å.
Step height in Å.
Roughness factor.
Average asperity depth made dimensionless with the spherical equivalent radius, a, specified inb.
CA observed in MD simulations.
Original Wenzel prediction.
Extended Wenzel prediction.
As with our comparison with experiments, examples exist for which the predictions of the extended Wenzel model do not agree with CAs observed in MD simulations. In some of these studies, the simulated CAs were larger than those predicted by the original Wenzel model, which may suggest that pinning effects were important.42,44
3. Conclusions
The Wenzel equation is often used to predict the CA for droplets in the Wenzel wetting mode on rough surfaces with surface features that are much smaller than the size of the droplet. The Wenzel model considers the roughness of the surface to amplify the solid–liquid and solid–vapor interfacial free energies but neglects the liquid volume stored in the asperities under the droplet. As such, it inherently overestimates the CA, particularly for larger asperities. In this work, we extended the Wenzel model by using a perturbation analysis to account for the liquid volume stored in the asperities of the surface pattern when they are small compared to the droplet size. By performing the analysis for two- and three-dimensional drops, we obtained the respective O(h) volume corrections to the Wenzel equation
| 44 |
| 45 |
which represent the central results of this paper. In the two-dimensional model, the radius of curvature of the cylindrical cap droplet remains unchanged to O(h) even as the CA is reduced. In the three-dimensional model, on the other hand, the O(h) reduction in the CA arising from the liquid volume stored in the asperities is accompanied by a concomitant O(h) increase in the radius of curvature of the spherical cap drop. The two-dimensional model was validated by comparison with the predictions of a computational model that has been previously shown to agree with the results from molecular dynamics simulations.26−28 The CA corrections advanced by the three-dimensional model help explain experimental observations of Barbieri et al.29 and results of MD simulations by Hirvi and Pakkanen,40 for which the observed or simulated CAs in the Wenzel model were mostly smaller than predictions of the original Wenzel model. By correcting the Wenzel CAs to account for the liquid volume stored in the asperities, the predicted CAs more closely match those observed in the experiments and simulations and help explain many of the commonly observed discrepancies between experimental results and predictions of the original Wenzel model.
Acknowledgments
M.B. is very grateful to Kelley Weber, Director of Library Services at Kansas Wesleyan University, for fulfilling the many interlibrary loan requests for reference articles related to this work.
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.0c00495.
The authors declare no competing financial interest.
Supplementary Material
References
- Cassie A. B. D.; Baxter S. Wettability of porous surfaces. Trans. Faraday Soc. 1944, 40, 546–551. 10.1039/tf9444000546. [DOI] [Google Scholar]
- Young T. An Essay on the Cohesion of Fluids. Philos. Trans. R. Soc. London 1805, 95, 65–87. 10.1098/rstl.1805.0005. [DOI] [Google Scholar]
- Wenzel R. N. Resistance of solid surfaces to wetting by water. Ind. Eng. Chem. 1936, 28, 988–994. 10.1021/ie50320a024. [DOI] [Google Scholar]
- Bartell F. E.; Shepard J. W. Surface roughness as related to hysteresis of contact angles II. The systems paraffin-3 molar calcium chloride solution-air and paraffin-glycerol-air. J. Phys. Chem. 1953, 57, 455–458. 10.1021/j150505a015. [DOI] [Google Scholar]
- Lundgren M.; Allan N. L.; Cosgrove T. Modeling of wetting: A study of nanowetting at rough and heterogeneous surfaces. Langmuir 2007, 23, 1187–1194. 10.1021/la060712o. [DOI] [PubMed] [Google Scholar]
- Erbil H. Y.; Cansoy C. E. Range of applicability of the Wenzel and Cassie-Baxter equations for superhydrophobic surfaces. Langmuir 2009, 25, 14135–14145. 10.1021/la902098a. [DOI] [PubMed] [Google Scholar]
- Koch B. M. L.; Amirfazli A.; Elliott J. A. W. Wetting of rough surfaces by a low surface tension liquid. J. Phys. Chem. C 2014, 118, 23777–23782. 10.1021/jp5071117. [DOI] [Google Scholar]
- Suzuki S.; Ueno K. Apparent contact angle calculated from a water repellent model with pinning effect. Langmuir 2016, 33, 138–143. 10.1021/acs.langmuir.6b03832. [DOI] [PubMed] [Google Scholar]
- Gao L.; McCarthy T. J. How Wenzel and Cassie were wrong. Langmuir 2007, 23, 3762–3765. 10.1021/la062634a. [DOI] [PubMed] [Google Scholar]
- Marmur A.; Bittoun E. When Wenzel and Cassie are right: reconciling local and global considerations. Langmuir 2009, 25, 1277–1281. 10.1021/la802667b. [DOI] [PubMed] [Google Scholar]
- McHale G. Cassie and Wenzel: were they really so wrong?. Langmuir 2007, 23, 8200–8205. 10.1021/la7011167. [DOI] [PubMed] [Google Scholar]
- Nosonovsky M. On the range of applicability of the Wenzel and Cassie equations. Langmuir 2007, 23, 9919–9920. 10.1021/la701324m. [DOI] [PubMed] [Google Scholar]
- Wolansky G.; Marmur A. Apparent contact angles on rough surfaces: the Wenzel equation revisited. Colloids Surf., A 1999, 156, 381–388. 10.1016/s0927-7757(99)00098-9. [DOI] [Google Scholar]
- Jopp J.; Grüll H.; Yerushalmi-Rozen R. Wetting behavior of water droplets on hydrophobic microtextures of comparable size. Langmuir 2004, 20, 10015–10019. 10.1021/la0497651. [DOI] [PubMed] [Google Scholar]
- Milne A. J. B.; Amirfazli A. The Cassie equation: How it is meant to be used. Adv. Colloid Interface Sci. 2012, 170, 48–55. 10.1016/j.cis.2011.12.001. [DOI] [PubMed] [Google Scholar]
- Bell M. S.; Fichthorn K. A.; Borhan A. Effect of gravity on the configuration of droplets on two-dimensional physically patterned surfaces. Langmuir 2016, 32, 3858–3866. 10.1021/acs.langmuir.6b01156. [DOI] [PubMed] [Google Scholar]
- Zeng Q. Size matching effect on Wenzel wetting on fractal surfaces. Results Phys. 2018, 10, 588–593. 10.1016/j.rinp.2018.07.010. [DOI] [Google Scholar]
- Hejazi V.; Moghadam A. D.; Rohatgi P.; Nosonovsky M. Beyond Wenzel and Cassie-Baxter: Second-order effects on the wetting of rough surfaces. Langmuir 2014, 30, 9423–9429. 10.1021/la502143v. [DOI] [PubMed] [Google Scholar]
- Grzelak E. M.; Errington J. R. Nanoscale limit to the applicability of Wenzel’s Equation. Langmuir 2010, 26, 13297–13304. 10.1021/la1016164. [DOI] [PubMed] [Google Scholar]
- Swain P. S.; Lipowsky R. Contact angles on heterogeneous surfaces: A new look at Cassie’s and Wenzel’s laws. Langmuir 1998, 14, 6772–6780. 10.1021/la980602k. [DOI] [Google Scholar]
- The Sage Developers . SageMath, the Sage Mathematics Software System. version 8.7, 2019, https://www.sagemath.org.
- Tuteja A.; Choi W.; Mabry J. M.; McKinley G. H.; Cohen R. E. Robust omniphobic surfaces. Proc. Natl. Acad. Sci. U.S.A. 2008, 105, 18200–18205. 10.1073/pnas.0804872105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nishino T.; Meguro M.; Nakamae K.; Matsushita M.; Ueda Y. The lowest surface free energy based on −CF3 alignment. Langmuir 1999, 15, 4321–4323. 10.1021/la981727s. [DOI] [Google Scholar]
- Hare E. F.; Shafrin E. G.; Zisman W. A. Properties of films of adsorbed fluorinated acids. J. Phys. Chem. 1954, 58, 236–239. 10.1021/j150513a011. [DOI] [Google Scholar]
- Cui X. S.; Li W. On the possibility of superhydrophobic behavior for hydrophilic materials. J. Colloid Interface Sci. 2010, 347, 156–162. 10.1016/j.jcis.2010.03.065. [DOI] [PubMed] [Google Scholar]
- Shahraz A.; Borhan A.; Fichthorn K. A. A theory for the morphological dependence of wetting on a physically patterned surface. Langmuir 2012, 28, 14227–14237. 10.1021/la3026304. [DOI] [PubMed] [Google Scholar]
- Bell M. S.; Shahraz A.; Fichthorn K. A.; Borhan A. Effects of hierarchical surface roughness on droplet contact angle. Langmuir 2015, 31, 6752–6762. 10.1021/acs.langmuir.5b01051. [DOI] [PubMed] [Google Scholar]
- Shahraz A.; Borhan A.; Fichthorn K. A. Wetting on physically patterned solid surfaces: The relevance of molecular-dynamics simulations to macroscopic systems. Langmuir 2013, 29, 11632–11639. 10.1021/la4023618. [DOI] [PubMed] [Google Scholar]
- Barbieri L.; Wagner E.; Hoffmann P. Water wetting transition parameters of perfluorinated substrates with periodically distributed flat-top microscale obstacles. Langmuir 2007, 23, 1723–1734. 10.1021/la0617964. [DOI] [PubMed] [Google Scholar]
- Murakami D.; Jinnai H.; Takahara A. Wetting transition from the Cassie-Baxter state to the Wenzel state on textured polymer surfaces. Langmuir 2014, 30, 2061–2067. 10.1021/la4049067. [DOI] [PubMed] [Google Scholar]
- Ebert D.; Bhushan B. Durable lotus-effect surfaces with hierarchical structure using micro- and nanosized hydrophobic silica particles. J. Colloid Interface Sci. 2012, 368, 584–591. 10.1016/j.jcis.2011.09.049. [DOI] [PubMed] [Google Scholar]
- Bico J.; Marzolin C.; Quéré D. Pearl drops. Europhys. Lett. 1999, 47, 220–226. 10.1209/epl/i1999-00548-y. [DOI] [Google Scholar]
- Zhao Y.; Lu Q.; Li M.; Li X. Anisotropic wetting characteristics on submicrometer-scale periodic grooved surface. Langmuir 2007, 23, 6212–6217. 10.1021/la0702077. [DOI] [PubMed] [Google Scholar]
- Fürstner R.; Barthlott W.; Neinhuis C.; Walzel P. Wetting and self-cleaning properties of artificial superhydrophobic surfaces. Langmuir 2005, 21, 956–961. 10.1021/la0401011. [DOI] [PubMed] [Google Scholar]
- Rahmawan Y.; Moon M.-W.; Kim K.-S.; Lee K.-R.; Suh K.-Y. Wrinkled, dual-scale structures of diamond-like carbon (DLC) for superhydrophobicity. Langmuir 2010, 26, 484–491. 10.1021/la902129k. [DOI] [PubMed] [Google Scholar]
- Puukilainen E.; Rasilainen T.; Suvanto M.; Pakkanen T. A. Superhydrophobic polyolefin surfaces: Controlled micro- and nanostructures. Langmuir 2007, 23, 7263–7268. 10.1021/la063588h. [DOI] [PubMed] [Google Scholar]
- Cwikel D.; Zhao Q.; Liu C.; Su X.; Marmur A. Comparing contact angle measurements and surface tension assessments of solid surfaces. Langmuir 2010, 26, 15289–15294. 10.1021/la1020252. [DOI] [PubMed] [Google Scholar]
- Hong S. D.; Ha M. Y.; Balachandar S. Static and dynamic contact angles of water dropled on a solid surface using molecular dynamics simulation. J. Colloid Interface Sci. 2009, 339, 187–195. 10.1016/j.jcis.2009.07.048. [DOI] [PubMed] [Google Scholar]
- Wang F.-C.; Zhao Y.-P. Contact angle hysteresis at the nanoscale: A molecular dynamics simulation study. Colloid Polym. Sci. 2013, 291, 307–315. 10.1007/s00396-012-2747-2. [DOI] [Google Scholar]
- Hirvi J. T.; Pakkanen T. A. Wetting of nanogrooved polymer surfaces. Langmuir 2007, 23, 7724–7729. 10.1021/la700558v. [DOI] [PubMed] [Google Scholar]
- Hirvi J. T.; Pakkanen T. A. Enhanced hydrophobicity of rough polymer surfaces. J. Phys. Chem. B 2007, 111, 3336–3341. 10.1021/jp067399j. [DOI] [PubMed] [Google Scholar]
- Yong X.; Zhang L. T. Nanoscale wetting on groove-patterned surfaces. Langmuir 2009, 25, 5045–5053. 10.1021/la804025h. [DOI] [PubMed] [Google Scholar]
- Gao S.; Liao Q.; Liu W.; Liu Z. Effects of solid fraction on droplet wetting and vapor condensation: A molecular dyanamic simulation study. Langmuir 2017, 33, 12379–12388. 10.1021/acs.langmuir.7b03193. [DOI] [PubMed] [Google Scholar]
- Ambrosia M. S.; Ha M. Y. A molecular dynamics study of Wenzel state water droplets on anisotropic surfaces. Comput. Fluids 2018, 163, 1–6. 10.1016/j.compfluid.2017.12.013. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.