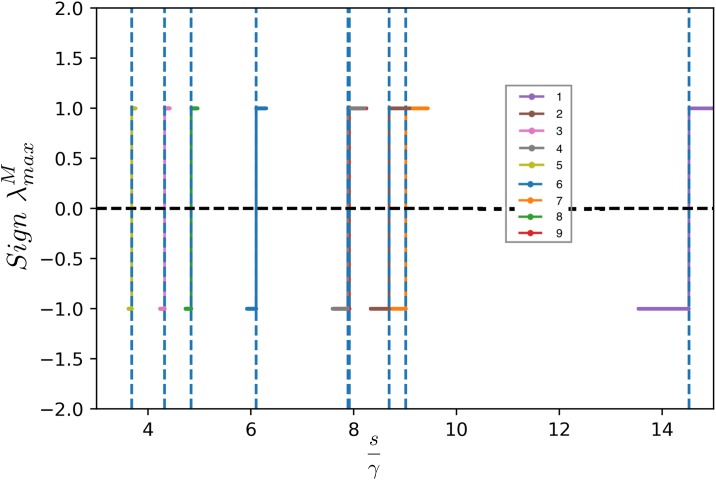
Fig 2. Plot of the sign of the maximum eigenvalue ${\lambda }_{max}^M$ of $\widehat{M}$ as a function of the interaction for real networks and constant value of the self limitation term s.

The inset of the figure indicates the number of the real network (1-9) shown in Table 1. The sign of the maximum eigenvalue ${\lambda }_{max}^M$ of $\widehat{M}$ changes as a function of $\frac{s}{\gamma }$ where γ is the coupling term and this change of sign occurs at μ_max = s where μ_max is the maximum eigenvalue of the matrix Γ of the corresponding network. This is represented by the dotted line in this figure, therefore the value of γ for which $Re\left({\lambda }_{max}^M\right)=0$ coincides with the condition of the singularity obtained with the solution to the fixed point equation discussed in Section, i.e. γ for which Re(μ_max) = 0 where $\Gamma =\gamma \widehat{A}$, for $\widehat{A}$ being the adjacency matrix. The networks analyzed are labeled according to the references in Table 1. (Notice that networks 4 and 8 are overlapping).