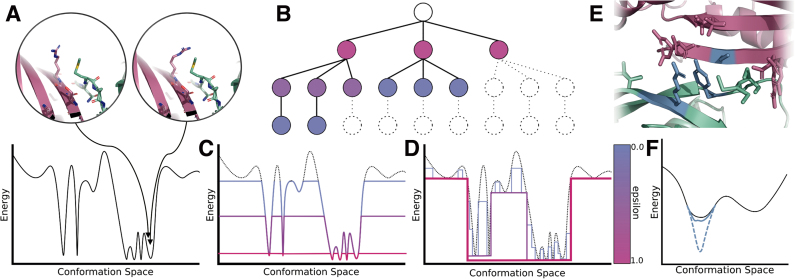
FIG. 2.

RK* and MAE exploit positive correlation between conformation and energy to efficiently bound the partition function. (A) Structurally similar conformations within the same energy well often have similar energies, shown as two points in the black energy landscape. (B) When the conformation space is represented as a conformation tree, some conformations (white leaf nodes) may be tightly bounded by computing bounds on their parent nodes (colored internal nodes). (C) Previous provable partition function approximation algorithms tightly bounded all conformations within some energy window of the GMEC. To decrease the error bound ɛ (colored by the scale beside D), these algorithms incrementally increased the energy window, computing exact energies for more and more conformations (colored curves). (D) RK* instead exploits the correspondence between conformation and energy to more efficiently bound similar conformations with bounds on regions of the energy landscape. As the error bound ɛ decreases and the approximation becomes more accurate (colored step curves), RK* iteratively tightens bounds on loosely bounded (and often low-entropy) regions of the landscape, rather than tightly bounding low-energy conformations. (E) Loosely-bounded pairwise-minimized bounds can affect a combinatorial number of conformations, shown as an ensemble of conformations that share the same sidechain assignments at the blue residues. Although the blue residues have favorable pairwise-minimized lower bounds, when all three are minimized in concert, their post-minimized energy is higher. (F) By computing a tighter bound on the three blue residues, MAE tightens the bounds on the combinatorial number of conformations containing the sidechain assignments at the blue residues. Thus, a loosely bounded energy well (black curve vs. dotted blue curve) may be bounded more tightly (solid blue curve) without minimizing all conformations in the well.