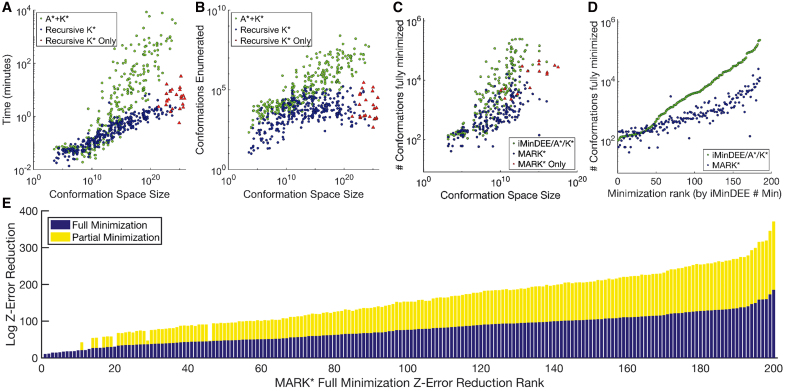
FIG. 4.

RK* and MAE both significantly improve efficiency over iMinDEE-A*-K*. (A, B) Times and conformations enumerated by MARK* (blue, red) and iMinDEE-A*-K* (green) plotted against conformation space size. When computing wildtype K* scores with rigid backbones and rigid rotamers, MARK* not only computes ɛ-approximate scores up to 3 orders of magnitude faster and 5 orders of magnitude more efficiently, it also completes design problems larger than was possible with iMinDEE-A*-K* (red triangles). (C, D) Number of conformations minimized by MARK* (blue, red) and iMinDEE-A*-K* (green) is shown, plotted against conformation space size (C) or full minimizations computed by iMinDEE-A*-K* (D, ranks for designs given in Table 1 of the Supplementary Information in Jou et al., 2019). MARK* completes 15 challenging design problems (size larger than 10¹⁰ conformations, red triangles) that iMinDEE-A*-K* cannot. MARK* minimizes up to 685-fold fewer conformations than iMinDEE-A*-K*, and is more efficient on the problems for which iMinDEE-A*-K* minimizes the most conformations. (E) Log Z-uncertainty reduction achieved by full minimization (blue) and corrections from partial minimizations (yellow) are shown as stacked bar charts. x-Axis shows design problems, sorted by Z-uncertainty reduction attributable to full minimization (ranks for designs given in Table 1 of the Supplementary Information in Jou et al., 2019). As the number of full minimizations increases, MAE efficiency increases, reducing Z-uncertainty by up to 3 orders of magnitude more than full minimization does.