Electronic Conductance Resonance in non-Redox Proteins

Abstract

Bioelectronics research has mainly focused on redox-active proteins because of their role in biological charge transport. In these proteins, electronic conductance is a maximum when electrons are injected at the known redox potential of the protein. It has been shown recently that many non-redox active proteins are good electronic conductors, though the mechanism of conduction is not yet understood. Here, we report single-molecule measurements of the conductance of three non-redox active proteins, maintained under potential control in solution, as a function of electron injection energy. All three proteins show a conductance resonance at a potential ~0.7V removed from the nearest oxidation potential of their constituent amino acids. If this shift reflects a reduction of reorganization energy in the interior of the protein, it would account for the long range conductance observed when carriers are injected into the interior of a protein.

Graphical Abstract

INTRODUCTION

Proteins are generally believed to be insulators, practically, because of the need to sustain high external electric fields,¹ and theoretically, because of strong vibronic coupling that traps carriers.² Nonetheless, there is ample evidence of long range electronic transport in proteins,^3–5 although almost all of these prior studies have focused on proteins that contain redox centers, because of their role in biological charge transport and because a considerable body of evidence suggests that optimal electron-tunneling pathways have evolved in these particular proteins.⁶ Motivated by a recent theoretical proposal⁷ that suggested unusual electrical properties might be a feature of all functional proteins (and not just proteins involved in electron transfer) we measured the electronic conductance of a series of non-redox active proteins. These proteins were maintained under potential control in solution, in conditions that preclude ion currents.^8–9 Their conductance was high and showed little decay with distance¹⁰, so long as charge is injected into the protein interior via ligands or other good chemical contacts. This property has important technological consequences. For example, protein molecular wires^8,11–12 are self-assembing and transport charge over longer distances¹⁰ than synthetic molecular wires.¹³ This conductance has been shown to depend on the conformation of a protein, so that enzymatic processes, such as DNA synthesis, can be followed dynamically with a direct electrical read-out.¹⁴ However, the mechanism of long-range charge transport in non-redox active proteins is unknown at present. The role that redox centers play in charge-transfer proteins has been demonstrated by electrochemical gating experiments,¹⁵ in which conductance is measured as a function of the electrochemical potential of the surface to which the protein is bound. In redox proteins, the peak conductance coincides with the known redox potential of the active site.^16–22 As first shown by Marcus,²³ solvent reorganization energy contributes significantly to the redox potential, and this depends strongly on the solvating medium. Here, we show the existence of a conductance maximum in three non-redox active proteins. The peak potential is almost the same in all three proteins studied, indicating a common transport mechanism. It occurs at a potential that is about 0.7 V less than the redox potential of aromatic amino acids in solution, suggesting that the effective Marcus reorganization energy is reduced by this amount when these same amino acid residues are enclosed in the interior of a protein.

RESULTS AND DISCUSSION

Controlling electron injection energy by changing the electrode metal

The calculated HOMO-LUMO gaps²⁴ of most proteins are large, so that the Fermi energy of a metal electrode should be far from that of molecular orbital energies if the Fermi level was located at mid-gap. However, interfacial polarization (and hence the location of molecular orbitals relative to metal Fermi energies) is difficult to calculate, so a robust method is needed to measure these energies. The energy of molecular states responsible for transport can be probed by measuring the conductance of molecules with different electrode metals.^25–26 In these prior studies, the metal work function served as a measure of the electronic injection energy. This approximation should not hold generally, because the surface potential of an electrode is extremely sensitive to chemical modification. Accordingly, the measurements reported here are carried out under electrochemical potential control, so that the rest potentials of modified surfaces can be used to quantify the changes in potential as surfaces are chemically modified.

The experimental arrangement is illustrated schematically in Figure 1a. A first electrode (Metal 1) is held at a potential V_r with respect to the reference electrode. A second electrode (Metal 2) is held at a potential V_b with respect to Metal 1. The molecule (M) sits in a nanoscale gap between Metal 1 and Metal 2. What is the potential of an electron when it passes on to the molecule from one of the electrodes? To begin with, we consider the case where both the reference bias, V_r, and the molecular juntion bias, V_b, are zero. The Fermi level of the reference electrode is pinned at the redox potential of the redox couple in solution, μ_REF by Faradaic processes that maintain constant polarization of the reference electrode surface. The reference, in turn, supplies or withdraws carriers from each of the metal electrodes (via low impedance connections) so as to move their Fermi levels, E_F1 and E_F2 into alignment at the energy μ_REF. The work function is defined by²⁷Ф = ϕ − E_F where ϕ is the rise in mean electrostatic potential across the metal surface, generated by the surface dipole (energies are expressed in eV). Accordingly, when the bulk electrochemical potential is changed from E_F to that of the reference, μ_REF, the change in ϕ is Δϕ = μ_REF − E_F. The potential difference seen by a carrier passing from the electrode to a molecule outside the electrode is given by Δϕ + ϕ_ads where ϕ_ads is the potential difference across an adlayer (which is assumed to be the same for both electrodes here). If the two electrode metals are not the same, then the net potential difference between the electrodes is Δϕ₁ − Δϕ₂ = μ_REF −E_F1 − (μ_REF − E_F2) = E_F2 − E_F1. If the molecule is assumed to sit in the middle of the electric field generated by this difference, then the total potential difference that a carrier experiences in moving from electrode 1 to the molecule is:

$$\Delta V=E_{F1}+{\varphi }_{ads}-\frac{E_{F1}-E_{F2}}{2}=\frac{E_{F2}+E_{F1}}{2}+{\varphi }_{ads}$$ (1)

with an identical expression for the case of a carrier moving from electrode 2 to the molecule. When only one electrode material is used, equation 1 becomes

$$\Delta V_1=E_{F1}+{\varphi }_{ads}$$ (2)

Figure 1:

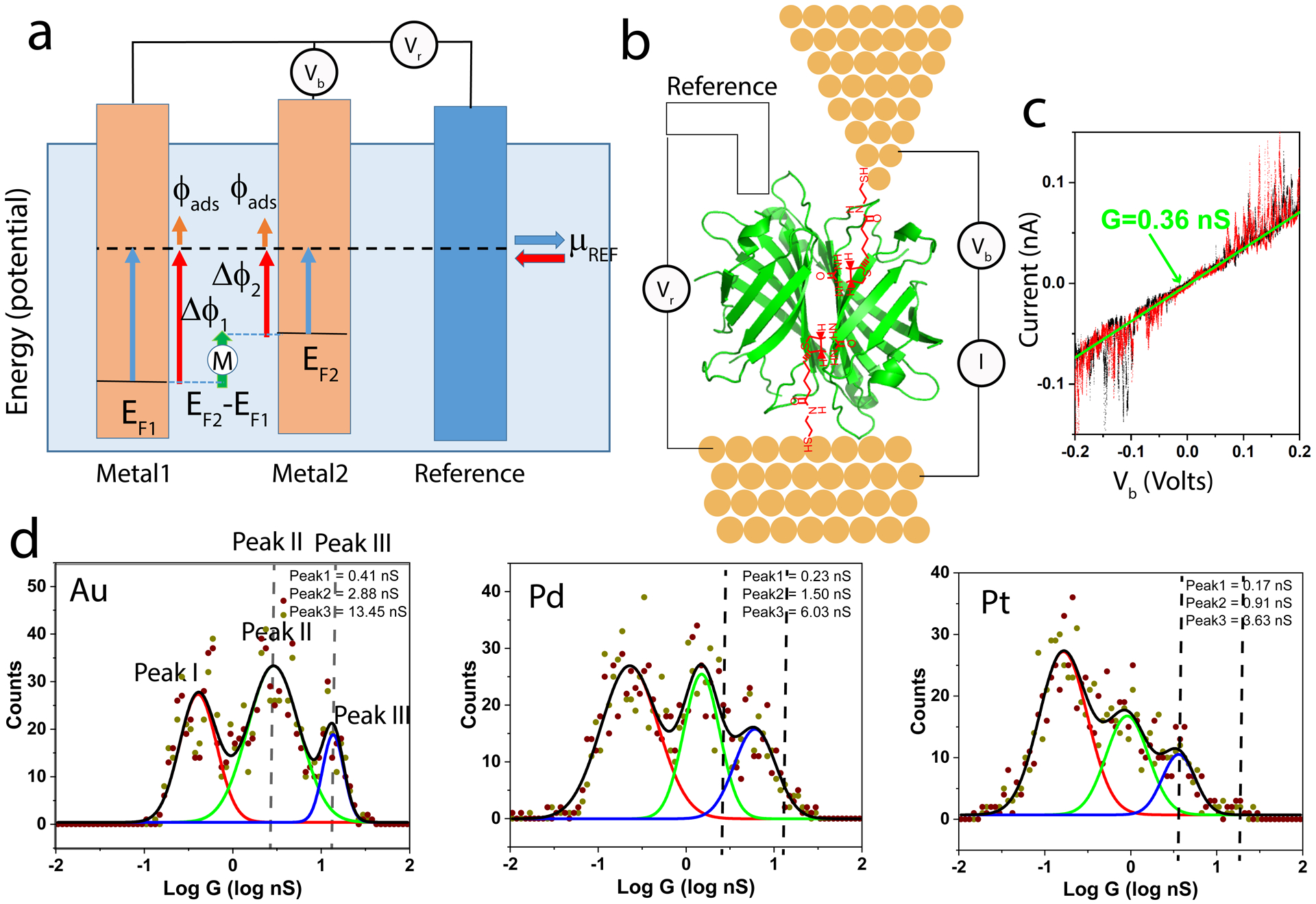
Measuring protein conductance under potential control. (a) Illustrating the surface potentials generated when two metals with different work functions are connected to a reference electrode. The molecule, M, is assumed to sit in the middle of of the potential gradient generated by the difference in surface potentials of the two metals. (b) STM measurement of protein conductance illustrating streptavidin protein (green) bound to electrodes by thiolated biotin molecules (red). The substrate is held at a potential V_r with respect to a salt-bridged reference electrode. For conductance measurements, a low (10mM) KCl concentration is used in the bridge, leading to a 360 mV difference with respect to the NHE. (c) Typical current-voltage (IV) curve for a single streptavidin molecule. Black data points are scanning up, red data points are scanning down. The green line is a linear fit yielding the conductance for this particular contact geometry. (d) Conductance distributions derived from many such IV curves for biotin/streptavidin on Au, Pd and Pt electrodes as marked. The dashed lines indicate the positions of peaks II and III in the distribution for the case of Au electrodes.

This quantity is the rest potential - the potential difference between the modified metal and the reference measured at infinite impedance (we translate these potentials to those refered to the Normal Hydrogen Electrode, NHE). For two different electrode metals, the average of the two rest potentials yields the right hand side of equation 1, and thus the potential difference experienced as a carrier moves from either electrode to the middle of the gap. For the case of two identical metal electrodes, this difference is given by equation 2.

Rest potentials were measured relative to a 3M Ag/AgCl reference (Figure 2a) using a high impedance voltmeter. Substrates were prepared by sputtering 205±5 nm of Pt, Pd and Au onto a silicon substrate coated with a 10 nm Cr adhesion layer. Ultraviolet Photoemission Spectroscopy (UPS - Figure S1, Table S1) was used to determine the work functions as 5.32 eV (Au), 5.02 eV (Pd) and 5.06 eV (Pt), values that are shown on Figure 2b as the points labeled UHV (Ultra High Vacuum). They have been converted to mV vs. NHE using the value of 4.625±0.125 eV²⁸ for the work function of the NHE (measurements were accurate to within a few percent - the error bars show the uncertainty in the NHE work function). These values change dramatically on contact with the 1 mM phosphate buffer used for conductance measurements (labeled ‘bare 1’ and ‘bare 2’, where two measurements on different samples are shown to illustrate the ±5% reproducibility). Subsequent modifications (Table 1, Figure 2b) have little effect on Pt, a small effect on Pd and a large effect on Au surfaces.

Figure 2:

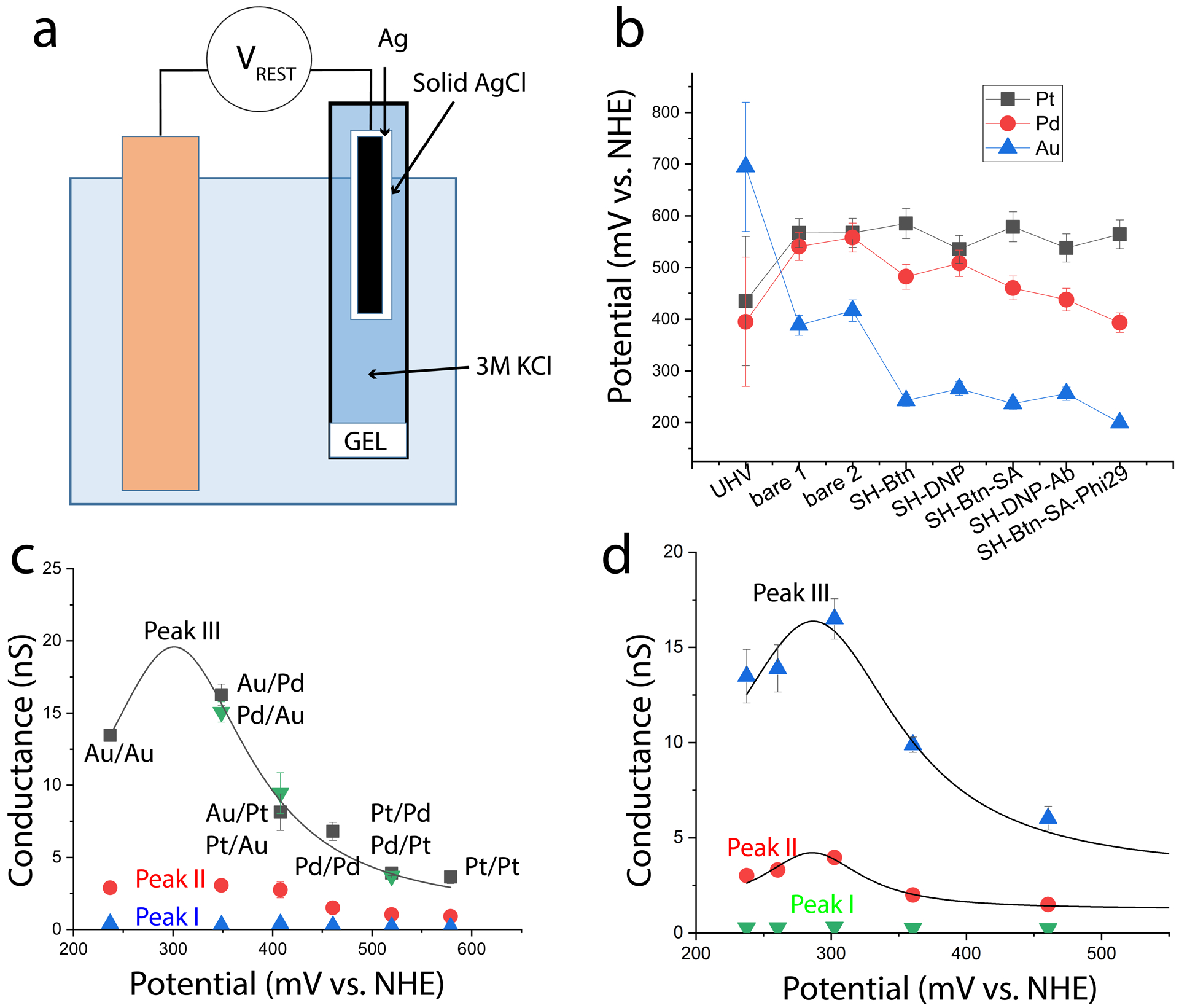
Streptavidin conductance depends on potential. (a) Rest potentials are measured using a high-impedance voltmeter (V_REST) connected between the electrode and a salt-bridged reference electrode. In this case the KCl concentration is 3M, corresponding to a 210 mV shift relative to the NHE scale. (b) Change in rest potentials with surface functionalization as decribed in Table I. Points from UHV are translated to the NHE scale using the work function of the NHE. (c) Conductance peak values for a streptavidin molecule as a function of electrode material (as marked, the first listed material is the STM tip, the second the substrate). Green triangles are for reversed combinations for the tip and substrate materials. (d) Conductance peaks measured as a function of potential (V_r in Fig. 1a) for streptavidin on Pd electrodes. Error bars in c and d are uncertainties in fits to the conductance distributions.

Table 1:

Rest potentials measured vs an Ag/AgCl reference with a 3M KCl bridge, converted to NHE by adding 210 mV.

	Description	Pt (mV vs NHE)	Pd(mV vs NHE)	Au(mV vs NHE)
UHV1	Plasma-cleaned films in UHV	435±1251	395±125	695±125
Bare chip 1 mM PB	Films under 1 mM phosphate buffer	566.8±3.82	540.7±17	388.4±4.3
Chip/SH-btn	Functionalized with thiolated biotin	585.3±0.2	482.3±0.1	242.5±0.7
Chip/SH-btn/SA	As above bound by streptavidin	578.9±0.4	460.5±1.9	236.8±0.6
Chip/SH-btn/SA/ϕ29	As above bound by a doubly-biotinylated ϕ29 polymerase	564.4±2.8	393.4±0.2	199.8±2.8
Bare chip (repeat)	Films under 1 mM phosphate buffer	567.6±3.3	558.5±1.8	417.2±1.8
Chip/SH-DNP	Functionalized with thiolated DNP	534.0±4.1	508.3±0.7	266.4±1.0
Chip/SH-DNP/Ab	As above + anti-DNP IgE	537.8±0.7	438.1±0.3	256.1±0.2

¹UHV data were measured to ±4 meV: the error quoted here (125 meV) represents the spread of values currently accepted for the work function of the NHE.

²Errors reflect stability of rest potential measurement. Repeat measurement (see bare chip repeat) indicates a run-to-run variation of ±5% (the error bars used in Figure 2b).

Conductance measurements were made by recording IV curves using an STM with a fixed gap and electrodes functionalized with ligands to trap the target proteins.⁹ The first system studied was streptavidin bound to electrodes functionalized with a thiol-terminated biotin⁹ (Figure 1b) for which the gap was set to 2.5 nm. Trapped proteins gave perfectly linear current-voltage curves, displaying characteristic telegraph noise above ± 100 mV (Figure 1c). Many repeated measurements of the gradient of these curves yield conductance distributions for all the contact geometries sampled, examples of which are shown for the three metals in Figure 1d. Contact resistance is smallest for the two higher conductance peaks (labeled peaks II and III) so we assume that these are the most sensitive to the internal electronic properties of the molecule. Both peaks move to lower conductance in going from Au to Pd electrodes, and to even lower conductance in going from Pd to Pt, illustrating the sensitivity of the conductance to electron energy, even in this non-redox active protein. We repeated these measurements with mixed electrode combinations (Au/Pd, Pd/Pt, Au/Pt) to obtain data points at three additional potentials (using potentials calculated with equation 1). We also reversed the metals used for the tip and substrate, finding that the conductance peak values were unaltered (though the height of peaks II and III changed a little, probably because of the more facile and mobile thiol bonding on Au substrates). Conductance distributions for all experiments are given in Figs. S2–S7 and the parameters extracted from Gaussian fits to these distributions are given in Tables S2 to S6. Results for the biotin-streptavidin junctions are summarized in Figure 2c. The data points for peak III have been fitted with a Lorentzian (as described in the discussion) to yield a peak at a potential of 301±3 mV vs NHE (with a full width at half maximum, FWHM, of 183±43 mV).

Controlling electron injection energy by changing the electrode metal

In the case of Pd electrodes, the region of potential free of Faradaic currents is large enough⁹ to allow² us to explore the resonance curve by varying the electrode potential (V_r in Figure 1a) in which case the carrier energy is given by adding V_r to the rest potential given by equation 2. The results of these measurements are shown for the biotin-streptavidin system in Figure 2d. The resonance for Peak III is fitted by an essentially identical Lorentzian to that used in Figure 2c for the case of different metals, with a maximum at 287±8 mV vs. NHE and a FWHM of 154±28 mV. The agreement between the two methods validates the assumptions used in the model for the changes in potential experienced with the different electrode metals.

As a check of reversibility, we ran a separate set of experiments in which a sample was analyzed at V_r = 0V on the 10mM KCl- Ag/AgCl scale, then again at -223 mV on the same scale, and then returned to 0V and re-analyzed. The results (Fig. S8) duplicated those presented in Figure 2d, demonstrating the reversibility of these measurements.

Resonances in other non-redox active proteins

Bivalent antibodies make excellent electrical contacts to electrodes functionalized with small epitopes, so we repeated our measurements using electrodes coated with a thiolated dinitrophenol (DNP) molecules that captured anti-DNP IgE molecules.⁹ Another system of technological importance is a doubly-biotinylated Ф29 polymerase trapped between streptavidin-coated electrodes.¹⁴ The streptavidin is connected to the electrodes using thiolated biotin (as in the example above). In both of these larger systems, the gap size was set to 4.5 nm. The antibody conductance distribution consists of two peaks (Fig. S4). The lower conductance peak (peak I) arises from one specific and one non-specific contact¹⁰ and it is dominated by contact resistance. This peak is unaffected by the carrier potential (red and green points in Figure 3a). Peak II arises from two specific contacts and has a much smaller contribution from contact resistance. This second peak depends strongly on potential. The peak of a Lorentzian fit to this potential dependence is again near 300mV (Table II). The polymerase distributions contain three peaks (Fig. S6) of which peaks II and III are sensitive to conformational changes in the protein.¹⁴ These two peaks are both affected by carrier potential, as shown in Figure 3b. Once again, the conductance peaks at a potential near 300 mV vs NHE. Fitting paramters are given in Table II.

Figure 3:

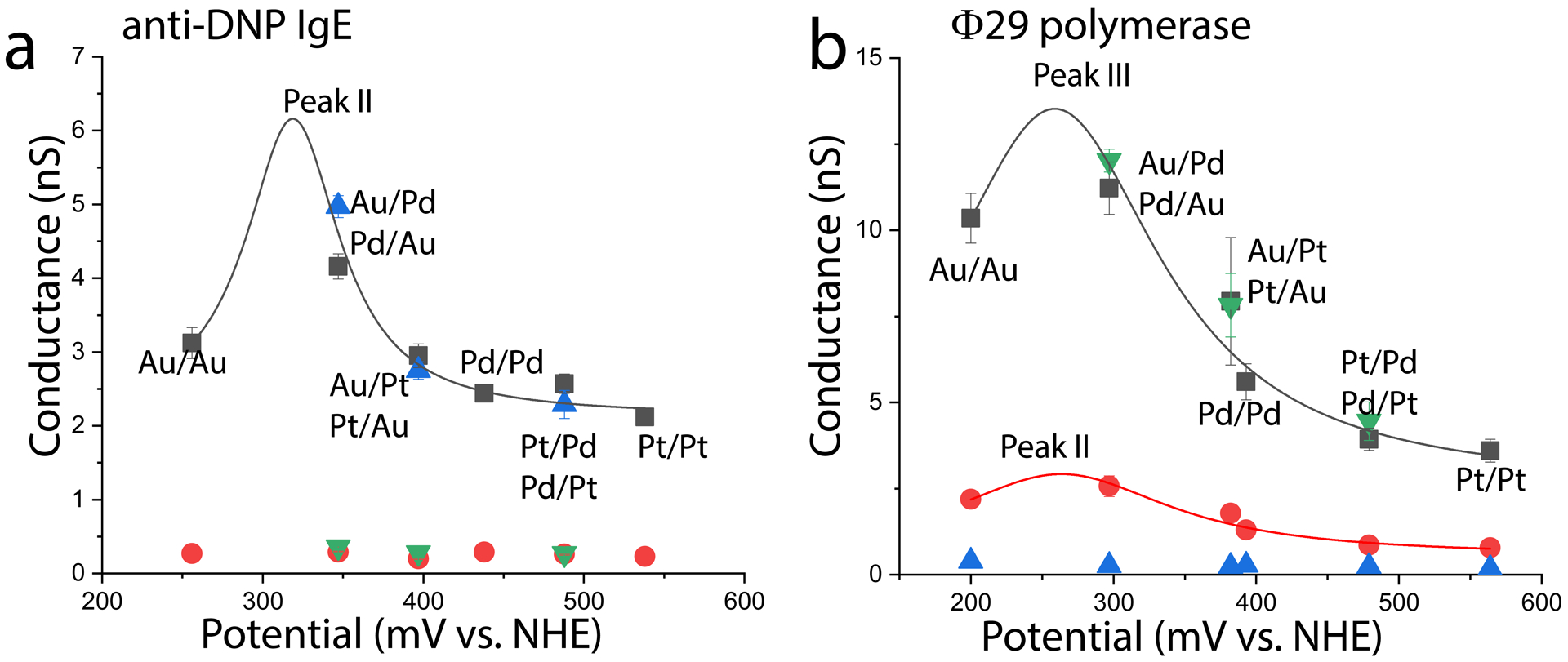
An antibody and a polymerase show similar dependence of conductance on potential. (a) Conductance of an anti-DNP IgE molecule for the electrode combinations shown (blue triangles are for reversed tip/substrate combinations). (b) A similar distribution for a doubly-biotinylated Ф29 polymerase trapped between streptavidin functionalized electrodes. Green triangles are reversed metal combinations. Parameters for the Lorentzian fits are given in Table II.

Table II:

Parameters of the Lorentzian resonance in 3 proteins. The peak width here is equal to 2Γ in equation 3.

Sample	Peak Energy (mV vs NHE)	Peak Width (mV)	R2
SH-biotin/SA - Electrochemical gating (Pk III)	287±8	154±28	0.991
SH-biotin/SA - Electrochemical gating (Pk II)	286±5	90 ± 16	0.984
SH-biotin/SA - different metals (Pk III)	301±3	183±43	0.994
SH-DNP/Ab - different metals (Pk II)	319±10	72±33	0.953
SH-biotin/SA/ϕ29 - different metals (Pk III)	259±6	183±33	0.989
SH-biotin/SA/ϕ29 - different metals (Pk II)	263±13	189 ± 64	0.962

CONCLUSIONS

Observation of a conductance resonance is unexpected in a non-redox active protein, if the redox potentials of amino acid residues are taken as a measure of the energy of molecular states in the protein. The observation of similar resonances in three electrochemically inert proteins strongly suggests that the same mechanism controls conductance in all three proteins, and that the energies of the molecular states responsible for transport are located at approximately +300 mV on the NHE scale. In the simplest model of resonant tunneling via a single electronic level, the dependence of conductance on electronic energy is described by the Breit-Wigner formula:

$$G\propto \frac{{\Gamma }^L{\Gamma }^R}{{\left(E_0-E\right)}^2+{\left({\Gamma }^L{\Gamma }^R\right)}^2/4}=\frac{{\Gamma }^2}{{\left(E_0-E\right)}^2+{\Gamma }^2}$$ (3)

The expression on the right-hand side is simplified by assuming that the coupling to the left electrode Γ^L is equal to the coupling to the right electrode, Γ^R(=Γ), as should apply to the symmetrically-bonded molecule geometry that gives rise to the higher conductance peaks in the present work. This is the Lorentzian function that has been fitted to yield the parameters listed in Table II, where the listed full width at half maximum is equal to twice the value of Γ in equation 3. The R² values suggest that this choice of fitting function is reasonable.

What could be the origin of a molecular level at ~300mV vs NHE? Although the specific chemical nature of the linker molecules alters the contact resistance, and hence overall conductance of the system, cyclic voltammetry shows that the linkers are not electroactive (as is also the case for the proteins used here).^{9, 14} Furthermore, the diverse nature of the chemical linkers is not compatible with the universal nature of the resonance reported here. Thus the resonance is most likely an intrinsic common feature of the proteins. We know that the conduction path is through the protein: this is shown by experiments that compare the responses of IgG molecules with the corresponding Fab fragment,⁹ that measure the internal decay of conductance with distance,¹⁰ and that sense the changes in conductance as streptavidin binds biotin⁹ or as a polymerase binds a nucleotide triphosphate.¹⁴ The question then is what common feature of these proteins might account for the resonance? The closest redox potential among the amino acids are those for the oxidation of tyrosine and tryptophan at about 1000 to 1200 mV vs NHE^29–30 (though the value can be lower, ~ 500mV, in deprotonated complexes³¹). All three proteins contain many of these residues in their interiors (Figure S9). Thus, the reduction of the Marcus reorganization energy barrier inside the protein (arising from non-ergodic sampling of electrostatic fluctuations proposed by Matyushov³²) could account for discrepancy between the redox potentials of these amino acids in solution and the conduction maximum energy in an intact protein. Similar reductions in reorganization energy have been reported for accessible redox centers that are at least partially embedded in protein or where charge transfer is rapid. For example, the redox potential of transition metal aqua-ions is reduced significantly if these same ions are incorporated into a protein³³ and the energy loss for rapid electron transport for primary charge separation in bacterial photsynthesis is reduced to 0.25 eV compared to the equilibrium value of 1.4eV.³⁴ Although the values of the peak-conductance potentials are nearly the same in all three proteins (Table II) one might expect the exact amount of reorganization energy to depend on atomic scale details, so the small differences observed may be significant. Deeper understanding of these effects requires detailed molecular modeling, and the streptavidin protein may be small enough to allow for calculations.

The observation of resonant tunneling (in the form of a resonance that fits the Breit-Wigner formula), and, in some proteins at least, long decay lengths¹⁰ and temperature independent conductance³⁵ might appear to be consistent with conduction bands as proposed by Szent-Gyorgyi,³⁶ but the possibility of long-lived quantum-coherence in proteins is controversial.³⁷ However, theories that extend the Landauer formula to finite temperatures can explain all of these features without invoking coherent transport.^38–39 In this modified Landauer approach, the Γ ‘s in equation 3 represent coupling between the electrodes and the nearest energetically-available molecular orbital. In a simple single-tunneling barrier model⁸ the electronic coupling is exponentially related to a bond lifetime, so stronger coupling (i.e., larger Γ) should correlate with stronger bonding (or equivalently a smaller dissociation constant, K_D). K_D for the DNP-anti-DNP IgE bond is 65 nM (Γ = 72 meV), and ~ 10 fM for streptavidin-biotin (Γ = 180 meV), qualitatively consistent with a relationship between bonding strength and electronic coupling (Table II).

Solvent-dependent reorganization would also explain another puzzle: why intact proteins can be excellent conductors, while hydrated peptide chains are excellent insulators.⁴⁰ The same mechanism might play a role in enhancing transport in the protein-clad stacked-heme molecular wire in geobacter sulfurreducens filaments.¹¹ However, we also note that any theory based on the Marcus approach is inconsistent with reports of temperature-independent conductivity.³⁵

EXPERIMENTAL SECTION

200 nm of Pd, Au or Pt were deposited onto a 10 nm Cr adhesion layer on one inch p-type Si wafers using an e-beam evaporator (Lesker PVD 75). Samples were cleaned in an electron cyclotron resonance microwave plasma chemical vapor deposition (ECR-CVD) system using mixture of H₂ (20 sccm) and Ar (2.5 sccm). Samples were transported via an UHV transfer line (5·10⁻⁹ Torr) from the ECR-CVD to a photoelectron spectroscopy chamber equipped with a differentially pumped helium discharge lamp (21.2 eV) for ultraviolet photoemission spectroscopy (UPS) with a working pressure of ~4–8·10⁻⁹ Torr. An Omicron Scientia R3000 hemispherical analyzer operated with a pass energy of 2 eV corresponding to an energy resolution of 3meV. A sample bias of 1.5V and energy offset of 2.7eV is programmed into the data acquisition software to compensate for the detector work function (4.2eV). Fits to the UPS spectra are shown in Figure S1 and a summary of work functions measured before and after cleaning is given in Table S1.

For the electrochemical measurements, salt-bridged electrodes were constructed as described previously⁹ using 3M KCl for the rest potential measurements (210mV on the NHE scale) and 10 mM KCl for the conductance measurements (360 mV on the NHE scale). Rest potentials were measured with a Fluke 177 meter (input impedance > 10⁷Ω) and potentials were stable to within ±5 mV over a period of hours. Sample to sample variation was ±5%.

High density polyethylene-coated Pd and Au probes were prepared as described previously.^{9, 41} For Pt probe preparation, a home-made etching controller was used, outputting an AC voltage of 30 V with a frequency of about 250 Hz. The etching solution for Pt probes was freshly prepared 10 M NaOH.⁴²

Substrates were prepared as described above, and functionalized as previously described.^{9, 14} Conductance measurements were made in 1 mM phosphate buffer, pH 7.4, using a PicoSPM (Agilent) following the procedure described elsewhere.⁹ Samples and solutions were prepared as described earlier for biotin-strptavidin⁹ and for the biotin-streptavidin-polymerase Ф29 system, using a doubly-biotinylated engineered polymerase.¹⁴ The preparation of all solutions, and characterization of substrate surfaces is also described in these earlier publications. FTIR spectra taken from all three metal substrates are given in Figure S10.