Figure 17.

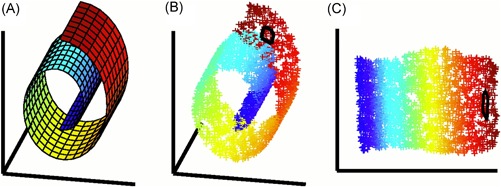
Example of nonlinear dimensionality reduction. Original caption: The problem of nonlinear dimensionality reduction, as illustrated for three‐dimensional data (b) sampled from a two‐dimensional manifold (a). An unsupervised learning algorithm must discover the global internal coordinates of the manifold without signals that explicitly indicate how the data should be embedded in two dimensions. The color coding illustrates the neighborhood preserving mapping discovered by LLE; black outlines in (b) and (c) show the neighborhood of a single point. Unlike LLE, projections of the data by principal component analysis (PCA) or classical MDS map faraway data points to nearby points in the plane, failing to identify the underlying structure of the manifold. Note that mixture models for local dimensionality reduction, which cluster the data and perform PCA within each cluster, do not address the problem considered here: namely, how to map high‐dimensional data into a single global coordinate system of lower dimensionality. Source: Roweis and Saul, 2000, Figure 1. Reprinted with permission from AAAS. [Color figure can be viewed at wileyonlinelibrary.com]