Automatic, Age Consistent Reconstruction of the Corpus Callosum Guided by Coherency from In Utero Diffusion-Weighted MRI

Abstract

Reconstruction of white matter connectivity in the fetal brain from in utero diffusion-weighted MRI faces many challenges, including subject motion, small anatomical scale, and limited image resolution and signal. These issues are compounded by the need to track significant changes in structural connectivity throughout development. We present an automated method for improved reliability and completeness of tract extraction across a wide range of gestational ages, based on the geometry of coherent patterns in streamline tractography, and apply it to the reconstruction of the corpus callosum. This method, focused specifically at addressing the challenges of fetal brain imaging, avoids depending on a tractography atlas and handles variations in size, shape, and tissue properties of developing brains, both between subjects and across ages. Although tractography from in utero MRI generally suffers from a significant number of misleading and missing pathways, we demonstrate the feasibility of extracting the coherent bundle of the corpus callosum while avoiding inappropriate diversions into other tracts.

I. Introduction

WHITE matter structural connectivity develops significantly throughout gestation, with critical transitions observable with magnetic resonance imaging (MRI) around 20 weeks gestational age (GA). Because of the challenges of imaging in utero and of producing accurate, long-range associations in structure, there is a need to establish robust protocols to determine connectivity patterns and their properties. Addressing these challenges through our proposed method can lead to a better understanding of healthy growth and the basic role that the structure of white matter (WM) plays in the functioning of the brain, as well as aid in clinical assessments from non-invasive MRI concerning how WM behaves in cases of atypical development compared to normal development [1]–[6]. In particular, the development of the corpus callosum may provide additional insight into a tract that is commonly the focus of intense study.

One of the more difficult challenges is motion [7], [8] from fetal mobility and maternal respiration. Techniques have been developed to iteratively correct for movement and reconstruct diffusion-weighted images (DWIs) from organizing subject orientations into a standard volume [9], [10]. While offering significant improvements in the motion-corrected images, the reproducibility of diffusion measures and tractography still poses more problems for in utero data [11]–[14] than postnatal or adult imaging. Other challenges are common to any imaging modality and for any subject, such as limitations to resolution and signal. Resolution limits are especially burdensome for fetal imaging because of the small length scales of the anatomy.¹ Scan time is limited to respect the comfort of the mother, which contends with the need to acquire more slices to accommodate potentially larger fetal movements. In addition, a larger within-slice field of view is required to encompass maternal anatomy in order to avoid fold-over artifacts, which both increases the required scan time and reduces the signal to noise ratio for the fetal brain.

Even with improved signal, changes in tissue response [15] pose additional challenges along the processing pipeline. For example, the anisotropy of the diffusion profile changes with the organization and myelination of connections [16], both locally within early-established WM tracts (as well as the cortex [17]) and on the scale of the whole brain as a richer architecture develops [18], [19]. Even with ideal DWIs, producing tractography for long-range connections faces several challenges. A well-established pitfall is that true structure is overwhelmed by false positives, at both the individual and bundled streamline (“fiber”) levels [20]. Such cases arise when a fiber continues along a path that is not associated with its original bundle, which can occur because of partial volume effects [21], [22] or simply the proximity of distinct, but transiently matching tracts. Other sources of diversions include radial glia and transient laminar zones [23], [24]. Not only do diverted fibers imply incorrect paths between regions, they obscure connections that should be stronger, especially when no fiber spans the entire tract.²

Ultimately, the challenges from in utero imaging necessitate corrective procedures to treat diverted fibers. Manual filtrations suffer from operator biases and errors, in addition to being labor intensive. For the spatial resolution, anatomical scale, and image quality available in MRI of adult brains, diverted fibers are commonly ignored entirely. In MRI of fetal brains, because partial voluming can be on the same scale as the width of the tracts themselves, omitting the diverted fibers that agree with the trajectory of the target tract for only a portion of their length would miss large tract sections and yield discontinuities.

Previous methods in adolescents and adults have shown success in extracting tracts by clustering fibers or regions of high fractional anisotropy (FA) to an atlas or common space [25]–[32]. However, building an accurate, age consistent fetal tractography atlas is difficult given the imaging challenges and developmental changes. Our proposed method would be a crucial step in constructing and refining such an atlas.

Similarly, fiber clustering shows promise in delineating distinct regions of postnatal and adult tractography [33]–[35], but is susceptible to errors in the presence of coherent diversions common in fetal tractography. For tracts like the corpus callosum (CC), with high curvature and branching diversions in fetuses, clustering approaches produce fragmented tracts.³ These fragments require additional geometric fitting (such as the method in Sec. II) and matching between fragments. Current approaches consider fibers as indivisible entities, but since the size of the anatomy already strains what can be resolved from in utero imaging, sections of a fiber may belong to separate tracts and should be treated accordingly.

Once tracts are properly identified and reconstructed, one can begin to probe developmental trends of scalar quantities, general tract shape, and refine interpretations of long-range connectivity. The development of diffusion properties in utero (e.g., FA and apparent diffusion coefficient) have been investigated both at the level of individual subjects and generalized scalar atlas-based regressions [16], [36]–[38]. A natural extension of the shape parametrization that we use to reconstruct a tract is to analyze the shape and the distribution of diffusion quantities, i.e. tract profiles. Such analyses have characterized tract properties in adults [28], [39–42], as well as infants [43]–[45]. We propose a new utilization of such a parametrization to adaptively extract and refine a coherent tract core. This approach reduces susceptibility to diversions and provides the benefit of inferring the shape of missing sections of tracts where many fibers are diverted out of the target tract, e.g. around the isthmus for the CC. This is difficult for methods that do not consider tract geometry both on the scale of local correspondences between fibers or the overall coherent shape.

To reliably identify an appropriate tract center, we propose a general algorithm for determining the medial line for a tract slice (described in Sec. II-B). Previous automatic methods, some specific to the midsagittal slice of the CC in adolescents and adults, can generate a medial line. The method from [46] uses radial lines emanating from the midsagittal slice centroid of the CC to “unwrap” tract within the planar slice, but this strategy is not applicable to tracts that do not wrap around their centroid. Alternatively, one could define two endpoints manually or by building a statistical model and associate points between the resulting two boundary segments [47], [48]. To avoid manual intervention or establishing a tract-specific model from a tractography atlas, we define corresponding points on opposite sides of a tract boundary.

We propose basic techniques to identify coherent portions in tractography that are based on the similar geometry present in local collections of fibers. These techniques are not sensitive to age and capture the variability between subjects of the same age without mapping to a tractography atlas. A more comprehensive exploration of other tracts is reserved for future studies, but the same fundamental principles of extracting bundles by modeling tract geometry still apply.

We demonstrate the effectiveness of the proposed method by reconstructing the CC, which can be verified with simple landmarks (although the method in general requires no landmarks). For the present study, we focus on the half-pipe shape of the CC for geometric simplicity and observe its development in the fetal brain from ≈ 20 – 36 weeks GA. While the general shape of the CC is assumed, tract shape and coherency is specific to each subject and does not rely on a tractography atlas, although the tissue and lobe segmentations are generated using established methods for label atlases (Sec. III-C).

Given an initial set of fibers from whole brain tractography, our method proceeds as shown in Fig. 1, detailed in Sec. II. First, we define a diffusion-parallel parametrization. Next, we remove inappropriate fibers and parametrize the remaining set to improve the parametrization quality. This cycle yields a conservative, coherent core. Finally, we produce an expanded reconstruction by iteratively refining the parametric surface that best describes the appropriate fibers.

Fig. 1.

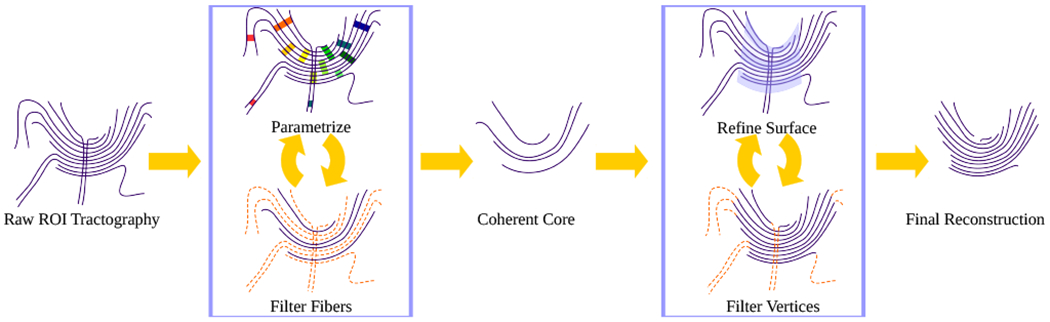
General flow of the proposed method on a simplified set of fibers: from raw tractography, through aggressive whole-fiber filtering for a coherent core, then by vertex-wise expansion for refinement of the reconstructed tract. Removed portions of the fibers are indicated by orange broken lines. Fibers have been drawn to show a clear projection in 2D, although the actual space is 3D.

II. Geometry-based tract building method

Our proposed method builds and refines a spatial model for a coherent fiber bundle, mapping fibers from physical locations to a normalized, tract-specific 3D parametrization p = (p₀,p₁,p₂). The parameter p₀ follows the diffusion-parallel direction of the fibers, from one end of the tract to the other. Both the width of the tract (i.e., the longest extent perpendicular to diffusion), p₁, and the thickness of the tract, p₂, are locally orthogonal to p₀.

A parametric volume is defined by a fourth-order regression for each coordinate having the form r(p) = (x(p), y(p), z(p)). The 2D core is the surface at the middle of the tract thickness (p₂ = 0.5). This geometric representation is similar to the cores considered by [28], [42] in children, but our specific approach and utilization differ, as described below. In building such a model, the reconstructed tract depends only on the quality of the tractography, not on the age or health of the individual subject. In the following, we propose quantitative scores for fibers and vertices along with the thresholds we find to be most appropriate.

A. Diffusion-parallel parametrization

First, we define the parametrization p₀ along the fiber paths, parallel to the principal diffusion direction. Similarly to other parametrization schemes (e.g., [39], [41]), we define corresponding points between fibers based on spatial proximity. To construct such a local set, we choose a single vertex and find points where nearby fibers pass closest (within 4 mm) to the selected vertex (Fig. 2). Seeding subsequent sets proceeds by choosing fibers that have the fewest points connected with the largest connected component.

Fig. 2.

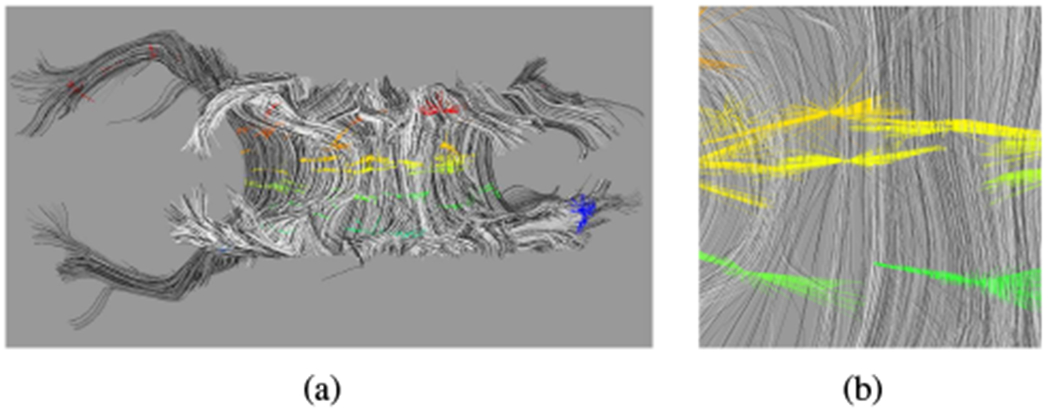
Intermediate step in parametrization for p₀ of a subject ≈ 32 weeks GA. (a) Sets of locally corresponding points. (b) Enlargement of (a). Colors correspond to the value of the parametrization of the set, from red at one extreme to blue at the other. Fibers are assigned a random grayscale shade for better distinguishability from neighbors.

The distance between sets is the average fiber length between the corresponding points for the shared fibers. The relative orientation of sets becomes a simple length comparison (Fig. 3(a)), which allows for a locally continuous parametrization p₀ to consistently span the connected component. The resulting parametrization is shifted and rescaled to the interval [0, 1], ignoring parametrization values more than one standard deviation from the mean to remove outliers.⁴

Fig. 3.

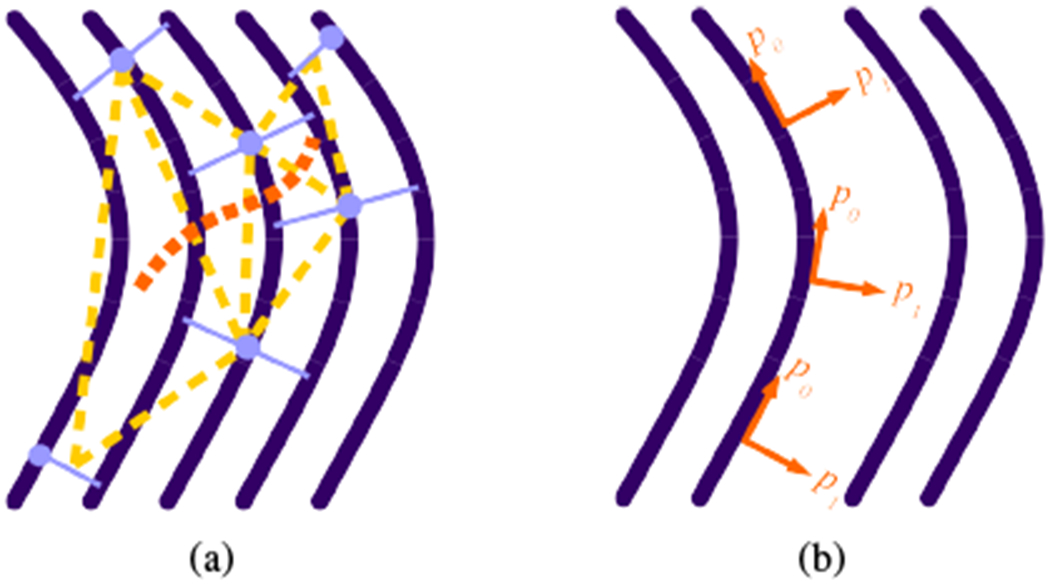
(a) Triangulation schematic. Dark purple solid curved lines are fibers; light purple solid straight lines are local correspondence sets; circles indicate the seed point for the set; light orange broken straight lines highlight a possible triangulation between the sets; the dark orange broken curved line follows a path through the triplets of sets to ensure a consistent tract-global parametrization. (b) Schematic of the local orientation of the direction of changing parametrization along a tract. While p₀ varies along the path of the fiber, p₁ only varies between fibers.

Diverging, converging, or drifting fibers can obscure an exact physical interpretation within parametrized space. However, the goal is to define a global, sequential relation between the paths of fibers that we can use to define a spatial model for the shape of the tract while highlighting portions of fibers that are not consistent with the general shape. Parametrizations based on arc length or some other landmarks may be applied once the final coherent bundle is successfully extracted.

B. Diffusion-orthogonal parametrizations

For our parametrization scheme, p₀ varies along a single fiber, but both diffusion-orthogonal parameters, p₁ for the width and p₂ for the thickness of a tract, are constant along a fiber, allowing the parametrization to spread or contract as necessary. Internal twisting (e.g., vortices along the tract, which can occur for nonplanar tracts like the cingulum where orientations of p₁ and p₂ vary along the tract) does not influence the endpoints of connectivity so is not considered.

Both p₁ and p₂ depend on the established p₀, as shown in Fig. 3(b). First, we project fibers into voxels at the resolution of the reconstructed DWI to create a boundary surface. Choosing a constant value for p₀ yields a nearly planar set of points, which we regress to a strictly planar 2D projection and associated boundary Ω from the intersection with the boundary surface. The problem of a spatially-sequential parametrization of the points within the boundary then reduces to defining a medial line to represent the core of the tract slice.

Our approach is based on the ratio R = ℓ/|a − b| of the path length ℓ between points between points a and b along the boundary Ω to their Euclidean separation. The maximum ratio R over all pairs of points on a boundary defines the first pairing of points that correspond on opposite sides of the tract. The original boundary curve splits into two closed curves at this opposing pair. The procedure repeats to iteratively bisect the boundary and define more pairs on opposing sides (Fig. 4). When tract shape leads to conditions where a new unique pairing cannot be produced (e.g., at a sharp turn) then vertices on the longer arc are associated with vertices on the shorter arc according to the fraction of the length between the previously established pairs that border the unpaired portion.

Fig. 4.

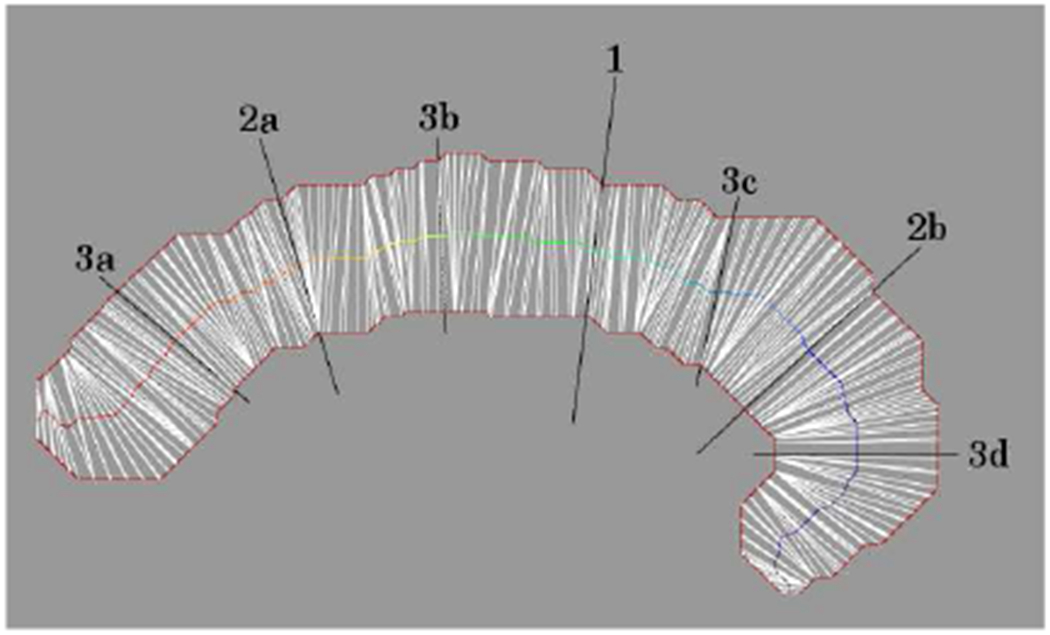
Medial line for a tract slice by pairing points (white lines) on opposite sides of the boundary (solid red outline). Extended black lines are pairings from the first three iterations. Numbers denote the iteration; letters label the distinct boundary segments when there is more than one.

A sequence naturally arises from the adjacency of points along the boundary from one tip to the other, with the midpoints of each pairing defining a medial line. The position of a fiber along the length of the medial line defines p₁, while a fiber’s distance from the medial line and its position relative to the trajectory of the medial line defines p₂. This approach produces a parametrization along the tract width (p₁) that is robust to misleading boundary segments.⁴

C. Coherent core extraction

The initial topology of the tractography with diversions can obscure the dominant coherent bundle. For a preliminary configuration, we construct multiple (25) p₀ for the raw ROI fibers. These initial trials vary based on the selection of the subset of fibers used in the sparsification step and the base vertices that define local correspondence sets. We assign each a numerical score and choose the best quality parametrization to initialize the extraction of the coherent core.

This vertex-wise parametrization quality q_i(p₀) is sampled at a finite number of p₀ values to evaluate the appropriateness of associating the parametrized point f_i(p₀) on fiber i to the other fibers in the bundle with the same value of p₀. The final fiber measure of quality is the average over the other fibers that have a point with parametrization p₀ at f_j according to

$$q_{ij}\left(p_0\right)=\frac{1}{N\left(p_0\right)}{\sum _j\left[\frac{\min \left\{d_i\left({\mathit{f}}_j\left(p_0\right)\right),d_j({\mathit{f}}_i\left(p_0\right)\right\}}{\left|{\mathit{f}}_i\left(p_0\right)-{\mathit{f}}_j\left(p_0\right)\right|}\right]}^2$$ (1)

where N(p₀) is the number of fibers that have been assigned a parametrization at p₀, and d_k(x) is the separation at the closest approach of fiber k to point x. The ratio is maximized when the pair of parametrized points match perfectly in local correspondence, and decreases as the points are shifted away from this matching. After establishing a reasonable parametrization p₀, we proceed by removing fibers that disagree with the dominating tract shape until a coherent core is established.

One indicator for a possible inappropriate diversion is when fibers extend beyond the parametrization limits of the dominant tract. Such cases are easily identified as a consequence of the choice of rescaling (Sec. II-A) by extremal parametrization values (0 or 1) for a significant portion of a fiber’s path. We empirically find a suitable threshold across subjects to be when about 40% of a fiber’s length is parametrized beyond the bulk of the core.⁴ A second indicator of a diversion is when the trajectory and parametrization of a fiber does not agree with the dominating path of the tract. Agreement is quantified by sampling each fiber at points (we chose five, evenly spaced) f_i along its length and comparing the difference in trajectory Δθ_ij(p₀) and difference in diffusion-parallel parametrization Δp_0,ij from that of the closest point f_j(f_i(p₀)) to f_i(p₀) in a representative subset of the current core. The agreement score has the form

$$A_i\left(p_0\right)=\frac{1}{W_i\left(p_0\right)}\sum _j{w}_{ij}\left(p_0\right)\left|\cos \left(\Delta {\theta }_{ij}\left(p_0\right)\right)\right|\left(1-\left|\Delta p_{0,ij}\right|\right)$$ (2)

where W_i(p₀) = ∑_j w_ij(p₀) is the sum over weights of other fibers, and the weights w_ij(p₀) are taken from the normal distribution at ||f_i(p₀) − f_j(f_i(p₀))|| with a standard deviation of 4 mm. We exclude a fiber if the agreement score falls below 0.2 at any sampled point along the fiber.

These two indicators are similar to those previously employed in filtering incompatible fibers from tracts in [28], but our treatment is more applicable to fetal data in that it does not require that fibers completely span the tract, and we do not rely on manual ROI definitions or construction of a tractography atlas. The fibers that these measures select for removal and the final set in combining these selections are highlighted in Fig. 5. Cleaning halts when no additional fibers are removed or upon reaching the maximum number of iterations.⁴

Fig. 5.

For the same ≈ 32 weeks GA subject from Fig. 2: (a) initial raw ROI parametrization p₀ from red at one extreme to blue at the other; (b) identification of fibers with extreme parametrizations; (c) identification of fibers which disagree with the mean direction; (d) combined filtering of fibers. For (b)-(d), fibers to keep are green; those that to excluded are red.

With this reasonably coherent core, the diffusion-orthogonal parametrization is applied to refine the tract based on its dominant geometry. Tracking the sign of $\widehat{\mathit{n}}\left(p_0,p_1\right)\cdot \ddot{\mathit{r}}\left(p_0,p_1\right)$ indicates the curvature of the fibers relative to the parametrization, where $\widehat{\mathit{n}}\left(p_0,p_1\right)$ is the surface normal at (p₀, p₁). This approach has two beneficial applications: (1) detecting flips in p₀ from confusing fiber trajectories and (2) detecting changes in curvature, which in the case of the CC corresponds to either the tapetum or inferior diversions into other tracts.

The former case arises when the initial topology is unclear or large gaps separate regions of the tract, identified by a change in sign along a curve of constant p₀ on the tract core surface. We correct such cases by reassigning p₀ of the smaller flipped fragments according to an extension of the surface from the largest self-consistent fragment. The latter case arises when other pathways dominate the desired simple tract geometry, and can be identified by a change in sign along a fiber, i.e., a curve of constant p₁ and p₂. In these cases, we truncate the tips of the fibers to keep only the central section over which the sign agrees with tract shape. Strongly corrugated tracts yield isolated ridges or grooves.

D. Expanding the coherent bundle

Given a reasonably coherent and geometrically accurate core, we proceed to expanding the coherent segment to fill gaps and to span the entire tract. We assign a score B_i to each vertex f_i of a fiber that penalizes greater distances from the surface and larger disagreements in the diffusion direction, having the form

$$B_i=\exp \left(-\frac{\Vert {\mathit{r}}_i\left({\mathit{f}}_i\right)-{\mathit{f}}_i\Vert }{\lambda }\right){\cos }^2\left(\Delta \theta \right)$$ (3)

where r_i(f_i) is the corresponding point on the regressed surface (the nearest point to f_i), λ is the length scale, and Δθ is the angular difference between the trajectory of the fiber at f_i and on the surface at r_i(f_i). We find a suitable exclusion threshold to be $B_i^{*}<0.15$.

This approach diverges from a similar method in [28] in that we utilize local direction information, as well as spatial proximity to the regressed p₀p₁-surface instead of an averaged sampling of points along fiber bundles. The vertex-specific nature allows us to retain sections of fibers that agree with the coherent core instead of excluding entire fibers.⁴

After expanding the coherent core, we evaluate the extracted tract for completeness. For conspicuously incomplete tracts, e.g., those that have too few fibers or spatial extent, the method is repeated from the initial p₀ parametrization with a new random seed, which may yield a more complete reconstruction. It is also possible to recover more complete tracts by repeating the entire cycle shown in Fig. 1 by supplying the previously extracted tract as the initial set of fibers to be parametrized for the coherent core; the expansion of the new coherent core proceeds as before, using the complete set of tractography fibers.

III. Data collection and preprocessing

A. Subjects and image acquisition

To evaluate the method over a range of GA, we use a set of scans collected as part of the University of Washington Fetal Brain Database, approved by the University of Washington Institutional Review Board (ID 00001931). Depending on recruitment timing, a subject was scanned in up to three separate sessions on different dates. Each scan has been screened for pathological development. We apply our method to a test set of 124 scans (70 male; 85 unique subjects, 45 male) of healthy subjects with GA ≈ 20 – 36 weeks for visual inspection to evaluate general performance. From this set, we focus on 34 scans (17 male; 30 unique subjects, 15 male) that span the 16-week range at roughly uniform density of one per week GA. The selected subjects are representative of the performance of the method with a typical frequency of cases that show small regions missing from the final structure where it is not supported by the tractography.

In utero DWIs were acquired using a 16-channel body coil in a 1.5 T Philips Achieva dStream scanner (software version R5) using multi-slice single shot EPI with SENSE factor 2. We set the resolution of a raw DWI volume to be 2.5 mm × 2.5 mm × 4 mm. Slices were planned to be approximately in the three anatomical planes (axial, coronal, sagittal) of the fetal brain, each time collecting three sets of one b = 0 and 15 b = 600 s/mm² (with the b-vectors distributed on the half-shell) and TE/TR = 125/5405 ms for a total of at least 3 · 3 · (15 + 1) = 144 volumes (135 sensitive to diffusion direction). Additional 48-volume (i.e., 3 · (15 + 1)) sets were acquired in the rare cases ( < 15%) of surplus scan time. Three additional b = 0 volumes were collected prior to each of the axial, coronal, and sagittal orientations to aid distortion correction, for a total of nine additional volumes. These reference volumes had not yet been included in imaging protocol for earlier scans (44 of 124).

B. Image volume reconstruction

Similar to [49], each of the three EPI-based DWI sets are non-rigidly aligned to a geometrically accurate and motion corrected T₂-weighted structural image to correct for susceptibility-induced geometric distortions. The relative signal level in each slice is normalized using a polynomial model to account for differences in scanner gain, coil sensitivity, and motion-induced slice-specific signal variations. Each DWI volume is co-aligned to a common anatomical coordinate system accounting for motion and manually inspected. Motion between individual slices is corrected using a diffusion-specific model-based alignment framework derived from [10].

Iterative 3D spatial deconvolution of the 3D reconstruction to combine information collected in different anatomical orientations is achieved using a model-based framework. This spatial deconvolution is combined with a simultaneous deconvolution in the space of diffusion directions. This process incorporates robust intensity rejection to address slices significantly impacted by through-plane motion induced spin history artifacts. The final reconstructed DWI has a 1.5 mm cubic voxel size and organizes the diffusion profile within a voxel into 64 directions. This 64-direction orientation map ensures oversampling of the three sets of 15 diffusion directions (one for each of the planned three slice planes), which together with fetal motion distributes measurements across more directions than a single axial-plane 15-direction gradient table.

C. Tractography and callosal ROI

As is common practice when considering voxel-level attributes, we infer coherent WM structure where a clear anisotropic diffusion profile exists. Water diffuses more readily in directions that are parallel to tracts and less readily orthogonally to tracts [50]. That a voxel’s diffusion profile corresponds to a coherent bundle is reinforced by reconstructing a consistent diffusion path across several voxels.

Our deterministic streamline tractography algorithm follows the principal direction from the ellipsoid fit to each voxel’s diffusion profile. We navigate this 3D field to produce tractography by integrating interpolated directions with an adaptive step size according to the Runge-Kutta-Fehlberg method (RKF45). Once fully traced, a fiber is downsampled to a constant step size. A fiber terminates upon encountering a voxel that either is not labeled as WM, or has FA less than 0.1, or by turning more sharply than π/2 rad/mm.

Whole brain tractography begins by seeding a fixed number of points (240) within the WM volume and associating the resulting fibers with the dominant peaks at each voxel along its path. The next iteration of seed points are chosen so that they will pass near local diffusion peaks that are not yet associated with any fiber. This yields comprehensive tractography that avoids the computational burden of identifying coherent regions within an unnecessarily dense volume of fibers.

Standard procedure for studying a particular tract involves a preliminary ROI and necessitates further filtering to exclude fibers that are not part of the target bundle. This can be accomplished using a second ROI, to be used as either an “and,” “or,” or “not” filter [51]. While using multiple inclusion ROIs has had some success for the CC [52], it can be problematic [53], and the additional challenges of imaging in utero compound the problems of misleading or incomplete fibers. Many fibers that intersect one ROI divert or terminate before intersecting with the second ROI. Removing whole fibers that are inappropriately diverted can leave gaps.

We automatically generate a midsagittal seed ROI from the intersection of WM tissue label with the boundaries between the left and right hemispheres of the frontal and parietal lobes. The callosal ROI is the largest connected component of these intersections (not necessarily strictly planar). We automatically generate the subject-specific tissue segmentations, as well as the hemisphere and lobe labels, from the T₂-weighted MRI reconstructions using an age specific fetal multi-atlas segmentation through a non-local patch-based labeling scheme (derived from [54]). While this segmentation differentiates WM from non-WM, it does not distinguish tracts within the WM, i.e. it is not a tractography atlas.

IV. Results

We observe improved performance from our proposed method over manually filtered tractography, shown in Fig. 6 with the initial ROI and preliminary filtering for a single subject. The raw ROI tractography in Fig. 6(a) shows prominent diversions from the CC into the cingulum and corticospinal tracts. This raw set of fibers was manually divided into two groups: (1) diversions into adjacent tracts to be removed (Fig. 6(b)), and (2) those that are mostly contained in the target CC bundle to be retained (Fig. 6(c)). This filtering represents the best performance from any current method that treats fibers as indivisible. Many of the diverted fibers in Fig. 6(b) include significant portions of the CC, and excluding them leaves gaps. For comparison, the automatic extraction of fibers using Eq. (2) shows in Fig. 6(d) the desired removal of diverted fibers, providing a more complete core for reconstructing the tract.

Fig. 6.

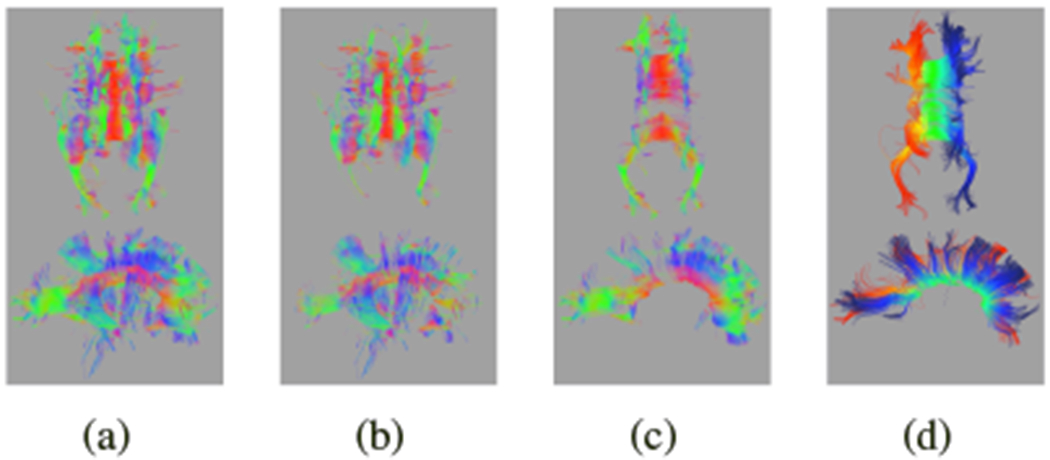
For the same ≈ 32 weeks GA subject from Fig. 2: (a) raw tractography that intersects the automatically generated ROI; (b) fibers removed after manual filtering; (c) fibers remaining after manual filtering. Colors indicate the primary direction of diffusion at each vertex. (d) Fibers remaining after automated filtering. Colors indicate the value of p₀ from red at one extreme to blue at the other.

In Fig. 7(a), we show the measure for each vertex [Eq. (3)] on the raw ROI tractography. Vertices with a high score that should be included are red, while vertices with a low score that should be excluded are blue. We show the full parametrization from the best reconstructed tract in Fig. 7(b)–(d). Figure 7(e) shows the noncallosal connections if we include all fibers from whole brain tractography that pass through voxels associated with the reconstructed tract.

Fig. 7.

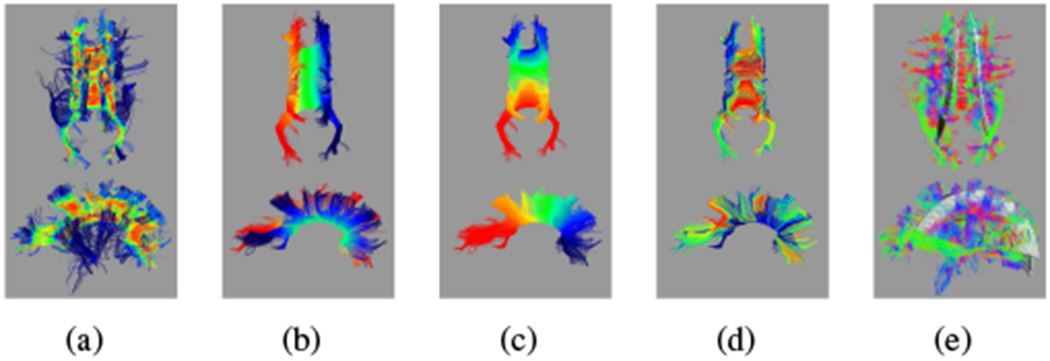
For the same ≈ 32 weeks GA subject from Fig. 2: (a) vertex scores [Eq. (3)]; red is a high score, blue is a low score. Middle panels show the refined tract with (b) p₀, (c) p₁, and (d) p₂. Colors show the value of the parametrization from red at one extreme to blue at the other. (e) Including all fibers that pass through voxels associated with the refined tract introduces connectivity not associated with the CC. Colors indicate the primary direction of diffusion.

Of the 124 usable DWI reconstructions from the broader set, 117 include a complete midsagittal cross section, including the isthmus, with only minor omissions at the tract extremities — commonly one of the posterior extensions of the forceps major (examples in Fig. 8).⁵ Of these 117 subjects, 96 show most callosal landmarks, with most of the remainder missing one half of the forceps major. Most importantly, all extracted tracts are free from diversions into adjacent tracts and map one side of the full tract to the other. Since the geometric model is specific to each subject, the reconstructed tract can adapt to variability in the orientation of the brain that arises from the initial alignment of the raw DWI or from drift during the DWI reconstruction.

Fig. 8.

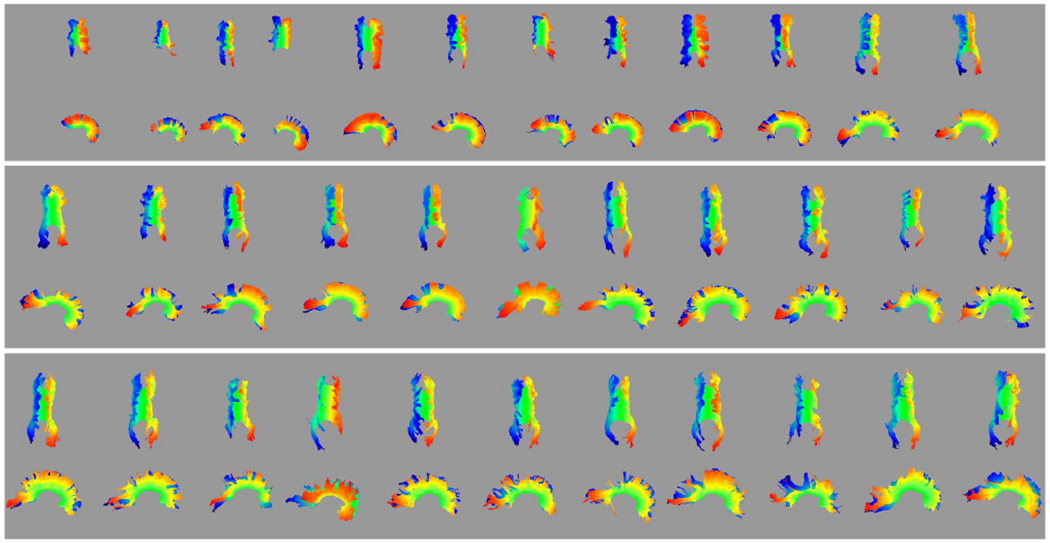
Automated reconstruction of the CC for individual subjects, ordered by age (youngest ≈ 20 weeks GA in the upper left to oldest ≈ 36 weeks GA in the lower right). Colors indicate the value of p₀ from red at one extreme to blue at the other.

On average, initial parametrizations of the 124 subjects produce a quality [Eq. (1)] of 0.61. Subsequent refinements produce average qualities of 0.78 for the coherent core and final reconstructed tract. Identifying the core removes an average of 55% of the sum of fiber lengths in the raw ROI. The removed portions would contribute to misleading connectivity. In expanding the coherent core to the final reconstruction, an average of 19% of the original length is recovered to offer a more complete representation of the tract.

While it is not the focus of this paper to comprehensively survey callosal properties, we can further verify the success of extraction by comparing diffusion measures between subjects using the reconstructed cores. Plots in Fig. 9 show trends for the change of FA with age. A solid circle represents the volume mean for each subject, while bars indicate the standard deviation within the volume of interest. For comparison, we show one trend for the voxels associated with the midsagittal boundary between lobes and another trend for the voxels associated with the reconstructed tract. We observe FA increasing approximately 1.0% per week within the medial ROI and 0.3% per week averaged over the reconstructed tract. These percentages are relative to the FA at 32 weeks GA (0.38 for the medial ROI and 0.23 for the tract average).

Fig. 9.

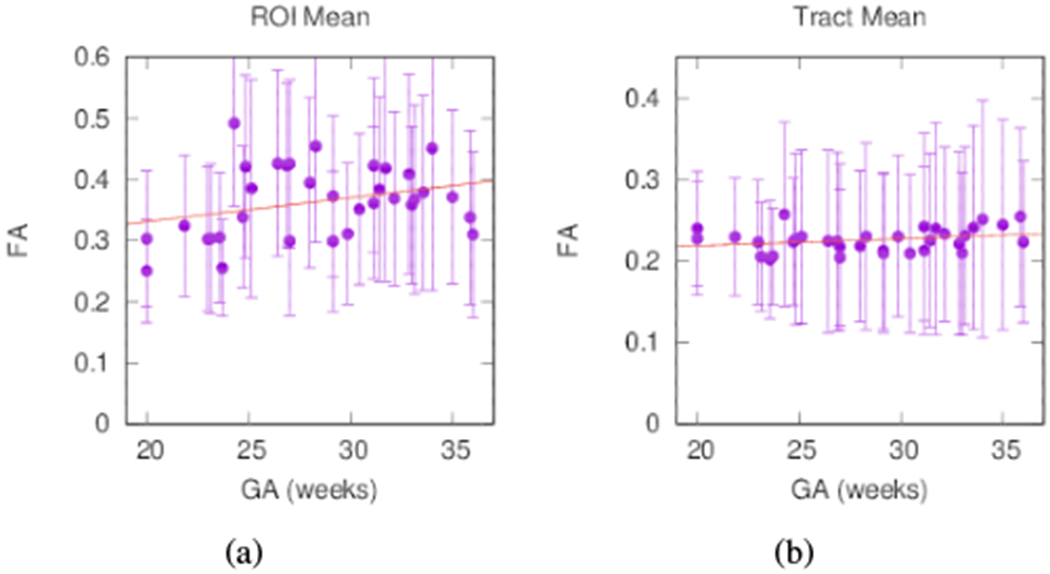
FA averages for individual subjects from (a) the midsagittal ROI with trend FA = 0.004 · GA + 0.252 (R² = 0.09) and (b) averaged over the reconstructed tract with trend FA = 0.008 · GA + 0.202 (R² = 0.07). Bars indicate the standard deviation within the volume of interest.

Measured FA varies along fiber paths (Fig. 10). To compare the properties of the CC between subjects, we transform the parametrization p that guides refinement of the reconstructed tract. Using the boundary between lobes to define the center of the CC, we measure the average FA across the width of the tract (p₁) at constant arc length in both directions. A pattern emerges in which the medial peak grows with subject age and stabilizes around 25 weeks GA.

Fig. 10.

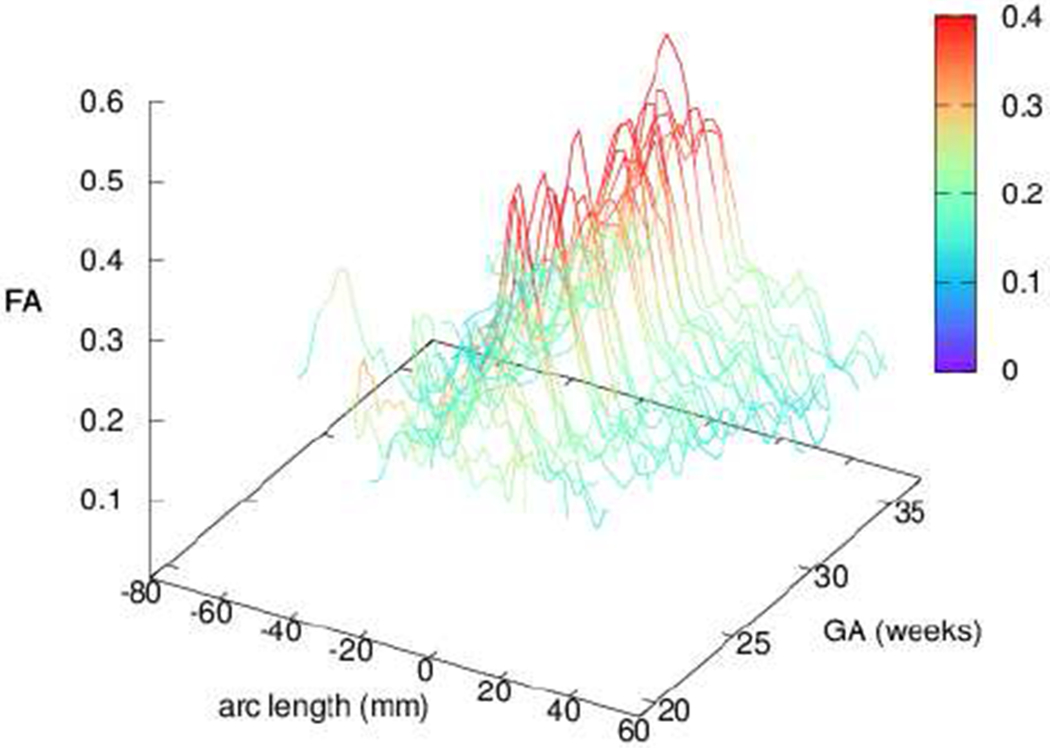
FA profiles of individual subjects along the principal direction of diffusion for the CC, averaged over the width of the tract. Profiles demonstrate a strong medial peak in agreement with [28], [37], [38]. Color is added for clarity in the profile height.

V. Discussion

The strength of our method is that it is based on the subject-specific geometry of coherent fibers, using a parametrization to model tract shape. This allows automated refinement of the tract, which we demonstrate over a range of 20–36 weeks GA, as well as further analysis of the tract’s diffusion measures and shape, including its context in general structural connectivity of WM. Because of its geometric foundation, the method does not require manual input or a tractography atlas, which for fetal studies would have to be age specific and contain enough examples to capture rapid changes in brain shape and contrast. This allows our method to be utilized as a basis for building a developmental tractography atlas for WM.

Tract cores that are reconstructed from DTI, as we present here, can also be used as a preliminary structural skeleton when considering multiple-peak or global registration approaches. With the ability to extrapolate tract shape into regions that are problematic to DTI tractography, one may be able to more precisely characterize the behavior of “unsuccessful fibers” [55] that can result from real developmental processes or reconstruction artifacts. Refinements to WM structure can be applied to further improve developing connectomes, explored in neonatal [56]–[60] and in utero [12] studies. Our method for refining coherent bundles is also appropriate for postnatal and adult data.

Building connectivity maps directly from fibers treats all fibers as equally valid; yet there can be significant systematic biases that lead to misleading bundles, particularly for tractography from images in utero. In general, whole brain connectivity studies do not consider the validity of a fiber in the context of major tracts, although there has been some success reducing false positives [61]. As a consequence of reconstructing major tracts to a fuller extent by respecting basic geometric constraints for fiber pathways, refinements to representations can be leveraged to reduce the contribution of false positives in identifying bundles and building connectomes.

Using more complete bundle shape also allows for alternative connectivity measurements (e.g. the direct measurement of strongly coherent bundles, or more accurate mappings between cortical regions and the shapes of these regions themselves) instead of relying entirely or in part on fiber count or average bundle quantities like FA [62]. Our method builds a more accurate and complete representation of the WM architecture, but it is beyond the scope of this paper to infer specific connectivity strengths or schemes (i.e., node choice, as explored in [63]–[66]. While the prevalent strategies for connectivity strengths intentionally avoid bundling tracts, there can be great benefit to utilizing the information from a complete tract to identify the large set of misleading fibers, which is more appropriate for the resolution limitations of in utero imaging.

The observed diversions from the CC into other tracts include the cingulum, corona radiata, fornix, optic radiation, inferior longitudinal fasciculus (entering from both anterior and posterior ends), and uncinate fasciculus. Lateral transcallosal projections [67] are observed occasionally in DTI tractography and can be much more readily observed when multiple directions are considered within a voxel, e.g. with constrained spherical deconvolution [68], [69]. We observe temporal projections via the tapetum (e.g., see [52], [70]) in the majority of fetal subjects; in some cases this pathway dominates so completely that all fibers from a midsagittal seed region of interest (ROI) are diverted away from the parietal cortex.

In addition to its geometric simplicity, opportunity to identify as early as 20 weeks GA, and previous studies with which to compare, we focus on the CC because of its central location in the brain and proximity to many other tracts. An application of the benefit of a complete, accurate reconstruction of the CC applied to a different tract is given in the supplementary materials.⁶ The coherent geometry of fibers is not directly considered in studies of whole brain connectivity via tractography, resulting in many diverted streamlines (Fig. 7(e)), which contribute to errors in the connectivity matrix. To verify the categorization of these fibers as erroneous diversions, future studies could investigate the prevalence of pathways that begin, e.g., in either the CC or the cingulum and end in the other.

Most previous studies have strongly anisotropic voxels from differences in dimensions for slice thickness and within-slice resolution, which biases measurements differently at different points along a tract. We reduce the effect of such a bias in our motion-corrected images by reconstructing cubic voxels using a deconvolution-based combination of multiple DWI slice orientations. However, cubic voxels are not required for to extract coherent bundles from tractography. While non-cubic voxels may introduce artifacts that depend on the path relative to the voxel grid, or affect measurements like FA along fibers from partial voluming, the local coherency in nearby fibers on which the method depends would remain.

Our observations of FA profiles of the CC show a medial peak, in agreement with previously reports. Reports of callosal FA in utero for a medial ROI span 0.3 [37] and 0.2 – 0.5 [38], while the tract average (including extremes) is lower, around 0.2 [16]. For neonates, callosal FA for a medial ROI is in a similar range, including reports of 0.38 [71], 0.4 [45], 0.34 – 0.47 [43], and 0.5 [44]; the tract average is again lower because of the lower FA at the tract extremities, from 0.1 [45] to 0.2 [44] and 0.22 [71].

Average trends for FA with age in utero, from 1.2% [36] to 1.6 – 3.5% [38], are also comparable to those of neonates 1.9 – 2.9% [43]. These rates of increase in FA, higher than the 1.0% that we observe, could be a result of partial volume effects at younger ages which can obscure the CC and result in lower FA measurements; however, verification would require additional analysis of the interaction with the adjacent WM volume and tracts. [28] reported similar FA profiles with a medial peak for adults, although FA values were higher (0.7 medially and 0.3 approaching the tract extremities).

Future studies could investigate the surrounding WM volume and nearby tracts to more accurately determine the role of partial voluming on FA profiles and trends with age. Other studies could investigate the intricacies of the spatial distribution of FA and other quantities across the tract as it is straightforward to adapt the parametrization p for a more detailed spatial analysis. However, obtaining correspondence between subjects would still require identification of landmarks to map locations between individual scans.

Some alternatives to diffusion tensor streamline tractography account for multiple orientations within a voxel, such as probabilistic tractography [72], [73] or spherical deconvolution [68]. However, streamlines can divert more often by introducing more than one diffusion direction in these higher order methods. Other alternatives focus on the global connectivity of the tract, e.g., through minimization of energy [74], [75], genetic approaches [76], or paths of least resistance for flows [77], [78]. Still, the particular challenges of in utero imaging can lead to inappropriate connectivity, and tract geometry is not addressed through these methods alone. While such methods offer improved tractography in some cases, the complications of crossing fibers obscure the local coherency in major bundles. Consequently, we have focused on a single tensor model for one diffusion direction per voxel to establish coherent tract cores. A subsequent application of our extracted tracts could be as a skeleton of dominant structures to explore more elaborate, higher order tractography.

VI. Conclusion

We present a method to automatically extract and reconstruct the CC from DTI tractography of in utero subjects from 20 – 30 weeks GA. Based on the geometry of the dominant coherent bundle, this method does not rely on the construction of a tractography atlas, or on manual definitions for seed regions or for fiber and vertex filtering. The reconstructed tract excludes diversions and avoids implying inaccurate connectivity, while providing a means to infer the full path of a tract. Both spatial profiles, which exhibit a strong medial peak, and general ranges for FA in the CC agree with previous observations for fetal and neonate subjects.

Our method is motivated by the challenges of imaging in utero, but its approach is also suitable for neonatal through adult brains because of its intentional feature of analyzing WM at different ages. This reconstruction method can serve as the foundation for future studies on general tract properties and structural connectivity in the developing brain, as well as a diagnostic aid in clinical settings. In extending the scope of our method’s application to other tracts, the basic techniques will still be a valuable tool for reliable extraction since the same rules for coherency apply.