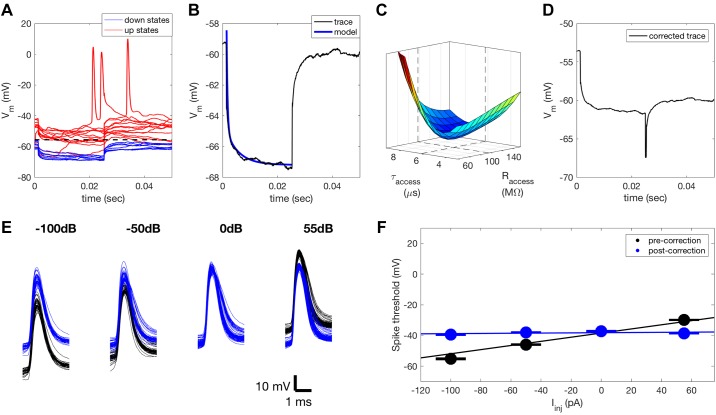
Fig. 1.
Compensation for access resistance. A: we injected a series of 40-pA current pulses into each neuron before each sweep. This allowed us to estimate both Raccess and Rinput from the change in Vm. Cycles of current injection that included an up state (red traces) were identified by crossing a threshold corresponding to the mean of the Vm distribution. These traces were excluded and the remaining traces (blue) were used to compute the mean Vm response to the current pulses. B: the mean Vm (blue trace) consists of fast and slow exponential components that correspond to Raccess and Rinput, respectively. A double exponential model was fitted to the mean Vm response to quantify the contribution of Raccess so that it could subsequently be compensated for. C: each fit showed a clear minimum in the error function for a range of resistance, Raccess, and time constant, τaccess, values. D: estimate of the true Vm in response to Iinj following compensation for Raccess. E: an estimate of the remaining Raccess following compensation was also obtained for each neuron by quantifying the change in spike threshold under different levels of Iinj. Spikes before (black) and after (blue) correction for Raccess using these two methods. F: a linear fit (black line) to mean spike threshold for different levels of Iinj (black circles, standard errors indicated by black lines) can be used to quantify Raccess. Error bars appear as a single line due to the minimal variation in threshold between spikes. After correction for Raccess, spike threshold is impacted far less by Iinj (blue), demonstrating that Raccess has successfully been compensated for. Iinj, injected current; Raccess, access resistance; Rinput, input resistance; Vm, membrane potential.