Abstract
The seismocardiogram (SCG) is a noninvasively-obtained cardiovascular bio-signal that has gained traction in recent years, however is limited by its susceptibility to noise and motion artifacts. Because of this, signal quality must be assured before data is used to inform clinical care. Common methods of signal quality assurance include signal classification or assignment of a numerical quality index. Such tasks are difficult with SCG because there is no accepted standard for signal morphology. In this work, we propose a unified method of quality indexing and classification that uses multi-subject-based methods to overcome this challenge. Dynamic-time feature matching (DTFM) is introduced as a novel method of obtaining the distance between a signal and reference template; with this metric, the signal quality index (SQI) is defined as a function of the inverse distance between the SCG and a large set of template signals. We demonstrate that this method is able to stratify SCG signals on held-out subjects based on their level of motion-artifact corruption. This method is extended, using the SQI as a feature for classification by ensembled quadratic discriminant analysis (QDA). Classification is validated by demonstrating, for the first time, both detection and localization of SCG sensor misplacement, achieving an F1 score of 0.83 on held-out subjects. This work may provide a necessary step towards automating the analysis of SCG signals, addressing many of the key limitations and concerns precluding the method from being widely used in clinical and physiological sensing applications.
Keywords: seismocardiography, cardiac monitoring, signal quality, time warping, ensemble voting
I. Introduction
THE gold standard for assessing bio-signal quality is an expert determination of whether the captured waveform is usable for its intended purpose. This already subjective task has been complicated by the proliferation of robust signal processing algorithms, which are able to extract data in the presence of noise. Consequently, clinical decision-makers now face a dilemma: how can we be certain that a bio-signal is of sufficiently high quality to be processed before this information is used to inform patient care?
One field that is substantially impacted by this problem is seismocardiography. Seismocardiogram (SCG) signals are waveforms captured with accelerometers and gyroscopes measuring vibrations of the chest wall in response to cardiac cycle events [1]. The contraction of heart musculature and subsequent blood flow yields signal features that correlate strongly with hemodynamic indicators such as pre-ejection period (PEP) [2], [3]. Because of this, SCG has shown potential to play an important role in outpatient cardiovascular monitoring [4], [5].
A major limitation of SCG for outpatient continuous monitoring is its sensitivity to noise due to motion artifacts [6]. Furthermore, the patient-specific nature of SCG due to physiological variability has made it difficult to identify a prototypical waveform [7]. This factor in particular makes it difficult to determine waveform quality before processing.
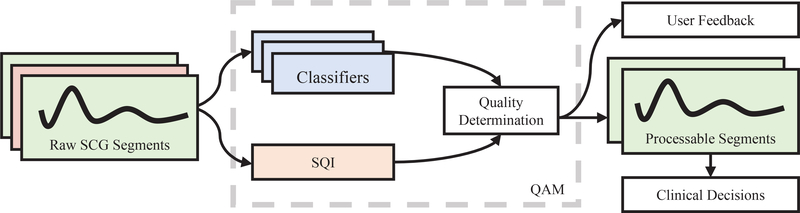
The ultimate goal of this work is to develop a flexible method for quality assurance of SCG signals that may be applied early in the processing pipeline to characterize the signal and obtain a beat-by-beat quality assessment. The concept of the proposed signal quality assessment module (QAM) is shown in Figure 1. The module is composed of two subparts: (1) a set of classifiers which identify categorical properties of the signal and (2) a signal quality index (SQI), which is a numeric indicator of general signal quality. The purpose of the classifiers is to identify properties of the source distribution of the signal, which are factors such as the patient’s activity or physiological state that may influence the SCG signal. This also includes factors external to the patient such as the environment or sensing system configuration, as will be explored in this work. By including a diverse set of such classifiers, one can obtain a holistic view of the signal, using it to determine whether processing should continue based on the error tolerance of the system. Since changes in the source distribution may not manifest as changes in general signal quality, and vice versa, the SQI is obtained as an additional metric on which to base a decision of whether or not to use the signal. Notably, this method would allow an investigator to fully tailor the QAM to their needs by selecting the most suitable classifiers and signal quality cutoffs.
Fig. 1.
Proposed quality assessment module. A set of signal classifiers identify properties of the SCG’s source distribution, while a SQI computes general signal quality. This information is synthesized to determine whether a signal can be processed, with high-quality segments being used to inform clinical decisions, and information about the signal’s source distribution used to deliver feedback to the patient, such as a warning of sensor misplacement.
In this work, we demonstrate the feasibility of such a QAM by presenting a novel, unified method for performing both quality indexing and classification of SCG signals from healthy subjects, even in the absence of a prototypical reference standard. To do so, we first define the SQI as a function of the inverse distance between the signal and a diverse set of reference templates, demonstrating its ability to stratify SCG signals based on their level of corruption with motion artifacts. As the performance of this SQI fully depends on the distance metric used, we introduce dynamic-time feature matching (DTFM) as a novel method of distance estimation, characterizing its improved performance for SCG quality indexing and classification compared to dynamic time warping (DTW), a ubiquitous method for bio-signal distance estimation. This SQI is compared against visual scoring, the current gold-standard. To perform signal classification, we extend this method by obtaining the SQI of a signal against diverse sets of reference signals, using the SQI as a feature for classification with ensembled quadtratic discriminant classifiers. To validate this method, we demonstrate the ability to both detect and localize SCG sensor misplacement on held-out cross-validation, a difficult classification task that had not yet been achieved. Together, these results support the potential for a unified, generalizable method of SCG quality assessment.
Prior work in SCG processing has focused on identifying and extracting fiducial points in the signal in the presence of noise, and thus few methods of signal quality assessment have been proposed. Because of this, manual annotation remains the gold-standard when validating signal analysis algorithms such as in [8]. Both [9] and [10] use feature extraction and outlier removal to eliminate low-quality signals, however such methods rely on accurate and consistent feature extraction to begin with, which may be intractable in noisy environments. In contrast, [11] proposes a SQI based on the relative signal power during the first and second heart sounds (S1 and S2). While the time-frequency characteristics of SCG are well-defined [12], they may not be informative about changes in waveform morphology. Notably, there has been significant work in pre-processing SCG to obtain valid signals, including signal decomposition [13], sensor fusion [14], [15], and averaging several beats to smooth noise [6]. Signal quality assessment is intended to supplement these methods, working synergistically to improve the quality of data.
The contributions of this work to current research include:
Introducing DTFM as a robust alternative to traditional DTW for SCG quality indexing and classification
Achieving consistent signal quality determination when the prototypical signal is poorly-defined
Detecting and localizing SCG sensor misplacement with ensembled quadratic discriminant classifiers
Unifying SCG quality indexing and classification to enable robust, generalizable QAMs.
II. Methods
A. Experimental Protocols
Data from two experimental studies were used in this paper, both conducted under a protocol approved by the Georgia Institute of Technology Institutional Review Board.
1). Protocol 1
The first study — which will be used to assess the proposed SQI in the presence of motion artifacts — is described in detail in [16]. This study was intended to identify changes in SCG signals corresponding to changes in PEP and included 17 healthy subjects (10 male, 7 female; age 26.1 ± 4.1 years; weight 66.1 ± 13.6 kg; height 168.2 ± 8.9 cm) with no known history of heart disease. Along with a reference electrocardiogram (ECG) and impedance cardiogram (ICG), a three-axis accelerometer and gyroscope were placed on the subject’s sternum to collect SCG waveforms. (Note that in the literature, the gyroscope-based measurements from the sternum may also be referred to as gyrocardiography, or GCG, signals [17].) The study consisted of four parts, in sequence. First, the subject stood upright and motionless for a five-minute rest period. This was followed by three minutes of walking at 4.83 kilometers per hour on a treadmill and 90 seconds of a squatting exercise. The exercise period was followed by a five-minute recovery period during which the subject again stood upright and motionless. Since the reference ECG for one of the subjects was corrupted, data from the remaining 16 subjects was used.
2). Protocol 2
The second study — which will be used to assess detection and localization of sensor misplacement — is described in detail in [18]. The study included 10 healthy subjects (5 male, 5 female; age 24.7 ± 2.3 years; weight 70 ± 10.5 kg; height 170 ± 11.6 cm) and was performed on two consecutive days. On the first day, accelerometers were placed in each of three locations: mid-sternum, 7.5 cm to the right, and 7.5 cm to the left. The subject stood motionless for 60 seconds followed by 60 seconds of a stepping exercise, after which there was a five-minute recovery period during which the subject again stood motionless. This method was repeated on the second day, with the sensors instead being placed on the mid-sternum, 5 cm above, and 5 cm below. ECG and ICG reference signals were also collected.
B. Signal Pre-Processing
Data from both studies were processed in the same manner. ECG and SCG signals were filtered with a finite impulse response (FIR) band-pass filter with Kaiser window, both in the forward and reverse directions to offset phase shift. Cutoff frequencies were 1–40 Hz for SCG and 0.5–40Hz for ECG. SCG signals were then segmented into separate intervals for each heartbeat by using thresholded peak detection to detect R-peaks on the reference ECG.
C. Generating Reference Templates
Much of this study relies on creating representative examples — called “templates” — of SCG signals based on sets of heartbeat-segmented waveforms. A standard method of generating templates is “Woody’s algorithm” [19], which builds on simple ensemble averaging by iteratively aligning and averaging signals in a set to produce a template t as shown in Algorithm 1. This property of Algorithm 1 is a clear benefit over ensemble averaging. With ensemble averaging, transient changes — and resulting nonuniformity — in signal morphology may reduce the quality of the resulting template.
The primary factor affecting the performance of a template is the quality of signals used to create it. For this reason, only SCG signals collected during resting periods were used to generate templates. In contrast, the value of m in Algorithm 1 does not greatly affect template performance; therefore, all available resting period segments were used to generate templates for each subject.
D. Overview of the DTW Algorithm
DTW is a method of estimating the distance between two signals that may be stretched or compressed relative to one another in time [20]. This property makes DTW well-suited to compare cardiac bio-signals, which may be compressed in time due to changes in heart rate and other hemodynamic factors. Prior work has utilized the DTW distance between ECG signals and reference templates as a feature for classifying ECG segments [21]–[23]. The principle behind such methods is that a signal from a certain source distribution will have a lower DTW distance to templates from the same source distribution than from others. Beyond ECG, DTW has also been used in motion analysis, including gait classification [24] and small gesture recognition [25]. As SCG is a cardiac signal describing mechanical motion, there exists precedent for applying DTW to SCG [13].
Algorithm 1.
SCG Template Generation
| 1: | procedure generateTemplate |
| 2: | t ← s1 ▹ Set first signal segment as template |
| 3: | for si ∈ {s2 . . . sm} do ▹ For each signal segment |
| 4: | Compute offset of maximum cross correlation: |
| 5: | |
| 6: | s* ← si(n – τ*) ▹ Align signals |
| 7: | t ← mean(t, s*) ▹ Update template |
In general, DTW stretches and compresses the two signals in time such that the Euclidean distance between the resultant signals is minimized [26]. It does this by identifying a mapping of points in one signal to corresponding points in the other, as shown in Figure 2(a). In the example, when a point in the signal is mapped to several points in the template (shown by blue shaded points in the matrix), this represents stretching of the signal relative to the template. Alternatively, when several points in the signal are mapped to a single point in the template, this represents relative compression of the signal. By extension, if points have a 1:1 mapping, no stretching or compression occurs. The resultant mapping is known as the “warp path”, as it describes the warping of the signals in time.
Fig. 2.
(a) The traditional DTW algorithm, showing the warp path (blue), 1:1 correspondence path (gray), and required points (black). Blue dotted lines show features brought into alignment after warping. (b) The DTFM algorithm. Square shading indicates candidate points (black), prohibited points (crossed), locations of time-series features (gray), selected path (green), and path from normal DTW (blue). Valid warp paths are shown as solid lines, blue for sub-optimal and green for optimal. In this example, the third maximum in the signal is determined to be aberrant, and the third minimum in the signal is mapped to the second minimum in the template.
The DTW warp path is subject to several fundamental constraints [27]. These include:
Boundary Conditions: The path must begin and end at opposite diagonal corners of the matrix.
Continuity: Given a point in the warp path, valid points for continuing the path include only adjacent (and diagonally-adjacent) cells in the matrix.
Monotonicity: The warp path must proceed between the diagonal boundary points without doubling back on itself, either vertically or horizontally.
In most applications, the warp path is subject to additional constraints, the most common being limiting the warping path’s allowable deviation from the diagonal (illustrated as the gray shaded squares in Figure 2(a)). Together, these constraints help prevent the generation of absurd mappings.
E. Overview of the DTFM Algorithm
Implicit in the mapping generated by DTW are assumptions about time-series feature correspondence — namely, local minima and maxima — as shown in Figure 2(a). Since SCG waveforms are highly prone to motion-artifact noise, the assumptions made by DTW in order to minimize the Euclidean distance may distort the true relationships between these features and ultimately underestimate the true distance between the signals.
To correct this limitation, we begin from the assumption that any valid mapping between an SCG signal and a template will necessarily match each feature in the template to a corresponding feature in the signal whenever possible. Because SCG is highly prone to motion artifacts in ambulant subjects, the number of features in the signal will exceed the template in the vast majority of cases. Figure 2(b) illustrates the DTFM method, which modifies the DTW algorithm to meet this assumption by imposing additional constraints on the warp path, supplementing the fundamental constraints. The algorithm performs the following:
Feature Identification: All local minima and maxima in the signal and reference template are identified. In the example, the rows and columns of the warping matrix corresponding to timestamps of the signal and template features respectively are shaded in gray. Points lying at the intersection of these rows and columns are referred to as “intersection” points; passing the warp path through intersection points results in matching a feature in the signal to a feature in the template.
Point Restriction: Next, prohibited intersection points in the warping matrix are identified, as shown with crossed squares in the example. A point in the grid is prohibited when passing the warping path through that point would result in either (1) matching a local minimum to a local maximum or (2) stretching the feature in the signal or template beyond some predefined limit.
Path Selection: Once all prohibited points are removed, remaining intersection points are denoted as “candidate” points, shaded in black in the example. As aforementioned, DTFM seeks to match all template features with a signal feature whenever possible; thus, valid warp paths are those that pass through a candidate point associated with each template feature whenever it is possible to do so — namely, whenever (1) the feature has corresponding candidate points and (2) doing so would not violate pre-existing constraints. The optimal path is then chosen as the valid path that minimizes the Euclidean distance between the warped signals.
Since there generally exists only one optimal warp path between any two points in the matrix — as defined by minimizing Euclidean distance — the set of valid warp paths is small in number. Therefore, it is possible to implement rapid, efficient methods of identifying all valid paths. An example pseudocode implementation is shown in Algorithm 2. In this procedure, the DTW warp path segments between each pair of valid candidate points (points between which valid paths exist) are recorded. Subsequently, all resulting continuous, grid-spanning paths composed of these individual segments are returned as valid warp paths. This is the DTFM procedure used to generate the results in following sections.
Algorithm 2.
Identifying Valid Warp Paths
| 1: | procedure validPaths | ||
| 2: | ≜ set of all template features | ||
| 3: | ≜ set of initial points of warp path segment | ||
| 4: | ≜ set of valid warp path segments | ||
| 5: | ← starting grid point p0 | ||
| 6: | for do | ||
| 7: | ← candidate points for fk | ||
| 8: | if then | ||
| 9: | for all valid pairs do | ||
| 10: | Get path between grid points with DTW | ||
| 11: | ∪ {DTW(bi,cj)} | ||
| 12: | ← valid candidate points, | ||
| 13: | ▹ Update segment starting points | ||
| 14: | Get paths between candidates and ending point pe | ||
| 15: | for do | ||
| 16: | ∪ {DTW(bi,pe)} | ||
| 17: | ← continuous paths in ▹ Valid warp paths | ||
Time-domain feature matching in DTW is a byproduct of Euclidian distance minimization rather than an explicit goal of the algorithm as with DTFM. In the following sections, we will show that this property of DTFM improves its performance for quality indexing and signal classification.
F. SQI using Distance from Reference Template
The proposed SQI in this work is a function of the inverse distance between a captured signal and a reference template, shown in Equation 1. Though any of myriad distance estimation methods can be used for this purpose — the quality of which determines the performance of the SQI — in this study we use either the DTFM or DTW distance.
| (1) |
where s and t are the captured signal and reference template respectively, D(·) is the distance function, L is the length of the warped signal, and λ is an optional distance penalty. This definition of a SQI matches intuition: unit SQI is achieved when there is no distance between the signals, and it approaches zero exponentially as the sample-averaged distance increases. Since the length of signals after warping may vary, L is intended to normalize the D by the length of the signal, yielding a distance-per-datapoint. λ determines the decay rate of the exponential term and thus only influences the range in [0, 1] in which scores commonly fall. In this study, we arbitrarily fix λ to 25 for all trials — as long as this value is chosen consistently, its effect on SQI stratification for different distance metrics is otherwise negligible.
Note that the reliability of the SQI is highly dependent on the quality of the template — since there is no reference standard for SCG, using a single template may not yield a valid SQI for all patients. Consider instead the set of templates . We can then define the SQI over the template set as
| (2) |
where is the number of elements in set . By increasing the size and diversity of the template set, Equation 2 becomes a more reliable SQI, as will be shown in the following sections.
Using a population approach addresses the problem of determining the quality of the templates themselves. This task may be intractable both due to the lack of an objective reference standard and because template quality may vary situationally. As the number and diversity of templates increase, the influence of low-quality templates is averaged and thereby diminished, while representative templates may drive the overall SQI higher or lower. This improves SQI stability without incorporating subjective assumptions about template quality. Notably, scaling the score of each template by a static value — related to its quality, for instance — would not change SQI performance; though the final value may change, relative scores assigned to the signals would remain consistent, as all scores are equally affected by scalar weights.
G. Evaluation of Proposed SQI
Evaluation of the SQI of Equation 2 will be performed both qualitatively and quantitatively.
1). Qualitative
As a visual example of how the SQI stratifies signals based on quality, we will show that the DTFM-based SQI visibly stratifies signal segments taken from the subjects’ different activity levels in Protocol 1, namely rest, exercise-recovery, squatting, and walking. These activities are listed in increasing order of typical SCG corruption; a valid SQI should therefore stratify scores for these levels such that an investigator may accurately discern signal corruption.
SQI scores were calculated using a held-out method. 16 templates were first generated from the resting period segments of each of the 16 subjects. For each held-out subject S, the template set was generated using the 15 templates from held-in subjects: . For each signal segment si belonging to subject S from all activity types, the SQI was then calculated as per Equation 2 using template set .
Once SQIs were obtained, the top 2%, bottom 2% and middle 50th percentiles of SCG segments were identified according to the DTFM-based SQI for one of the subjects in Protocol 1 during each of the rest, exercise, and exercise-recovery periods. These results will demonstrate that the SQI goes beyond simple activity recognition by identifying high- and low- quality segments during each activity type.
2). Quantitative
To analyze the performance of the SQI with increasing template set size, we perform the following method for each set size n, n ∈ [1,15]. For each subject S, we first chose n template sets at random from the 15 held-out sets to form the truncated set . This set was then used to compute the SQI of Equation 2 for all segments si belonging to subject S. Once this process was repeated for all 16 subjects, the scores for all subjects were combined into four vectors, one for each activity level.
To determine whether there was significant stratification present between SQIs for the four activity levels, and to what extent, the Friedman test was used [28]. The Friedman test is a non-parameteric test for determining the separation amongst data from different classes. Generally, a larger Friedman test statistic denotes higher separation between the levels, however it does not give insight into pairwise separation. To obtain this insight, we applied post-hoc analysis by using a Wilcoxon rank-sum test. As described in [28], this test returns the probability (p-value) that the separation between each pair of levels was achieved by chance. In this study, a p-value of less than 0.05 indicates statistical significance.
Since there may be numerous ways to select a subset of the 16 templates for each set size n, many combinations of templates were sampled at each step, up to 1000 combinations (not all set sizes had a large number of available combinations). This yielded up to 1000 trials for each n, with the Friedman and pairwise test results recorded for each trial. The process was performed twice, once using each distance metric.
H. Visual Scoring of SCG Segments
Visual scoring of the SCG segments was performed to compare against the SQI. To do so, 10 annotators with experience processing SCG signals were asked to assign signal segments a score of 0 (worst) to 1 (best) based on their quality. To aid in consistency, the following heuristics were provided:
If the impulses likely corresponding to both AO and AC are clearly visible, score greater than 0.75.
Otherwise, if either impulse is clearly visible, score greater than 0.5 but less than 0.75.
Otherwise, if either impulse is somewhat visible, score greater than 0.25 but less than 0.5.
Otherwise, score less than 0.25.
Annotators were encouraged to supplement these heuristics with their own judgment to determine the precise score. The annotators were assigned 1000 randomly-selected signal segments from the dataset, evenly-selected from each activity level. The final score for each segment was the sample mean of the available annotators’ scores, as before.
These scores were analyzed using the same method as described in the previous section; specifically, the Friedman test with Wilcoxon rank-sum post-hoc testing was used to determine overall and pairwise score stratification. To visualize the effect of the number of human annotators on score stratification — as with the SQI — this analysis was performed using subsets of the annotators with increasing size, from 1 to 10. For each set size, the test statistics were computed using scores from all possible combinations of annotators.
Finally, to assess whether the above heuristics for manual annotation were reflected by the automated SQI, the SQI assigned to each segment using all 15 template sets was plotted against the average score given to each segment by the 10 annotators. Using linear regression, a single best-fit line was generated for this data, and the R2 value of the linear fit was determined for each activity level. As detailed in [28], R2 is the ratio of the variance explained by the linear fit relative to the total variance; a higher R2 thereby indicates a stronger relationship between the two scores.
I. Signal Classification with Ensemble Voting
To determine an appropriate classifier for SCG signals, we start with the assumption that signals drawn from a source distribution — or class — will generally receive a higher SQI from templates created from the same class compared to others. If this assumption always held true, classification would be quite simple: given N classes, we define a template set where ti is a template created from signals from the ith class. Classifying the input signal s could be determined by
| (3) |
where is the class of s predicted by template set . The selected class is therefore the value of the argument i which maximizes the SQI. In reality, since there is no known prototypical SCG signal, the classifier may not generalize well due to its high dependence on template quality.
One way to compensate for template quality variability is to determine the prior likelihood of the template to give a certain SQI to signals from each class. To do this, we re-frame the classification problem in Equation 3 as
| (4) |
PY |X is the probability that the true class of s is Y given the vector x of SQIs assigned to the signal by the template set. Using Bayes’ rule, Equation 4 is equivalent to
| (5) |
since we are given x, and we assume that all classes are equiprobable. This probability distribution may be learned based on training data, a technique called Bayes estimation. The learning process may be greatly accelerated by imposing assumptions on the probability distribution; among the most common types are linear discriminant analysis (LDA), in which the distributions are assumed to be Gaussian with fixed covariance across classes; and quadratic discriminant analysis (QDA), in which the covariance restriction is lifted [29]. In this work, we utilize QDA in order to model potential relationships between templates in a set.
Even with Bayesian methods, accurate classification with Equation 5 still relies on the quality of the template set, and thus is a weak classifier. However, predictive performance of this method may improve by using ensemble prediction. Ensemble prediction is a robust technique whereby several weak classifiers act in unison to generate stronger predictions [30]. Ensemble methods have long been applied to cardiac signal processing, especially ECG [31]–[35]. As predictive performance of an ensemble classifier relies on diversity of its members, methods such as bagging and boosting are often employed during training. In this work, diversity was induced by increasing the number of template sets, and thus no boosting or bagging methods were used. Once the classifiers are trained, their individual predictions are combined to produce one prediction from the ensemble [30].
To apply ensemble prediction to this method, consider the superset M composed of unique template sets such that where |M| is the number of template sets. After training each classifier as per Equation 5, we can obtain a majority vote from the superset M on signal s as
| (6) |
which returns the most common prediction across all templates in set M. An overview of this method is shown in Figure 3. By selecting diverse template sets — such as by constructing each template set from a different subject’s data — the generalizability of this model improves, becoming less sensitive to the quality of any individual template. This property is valuable in SCG processing, as quality templates are difficult to identify.
Fig. 3.
Overview of ensemble voting with template sets. A template set is composed of a group of templates, each derived from SCG signals belonging to a different class. Each template assigns the incoming signal a SQI. For each set, the SQI values are mapped to the most likely classification (accounting for variability in template quality), which represents the vote of the template set. The final prediction is the mode class of all template set votes.
J. Evaluation of DTFM and DTW Algorithms
We will contrast the DTFM and DTW algorithms using both qualitative and quantitative methods.
1). Qualitative
We will provide an example of how the DTFM and DTW warp paths differ for a SCG signal segment taken from the resting period of a subject in Protocol 1. The optimal warp paths will be contrasted, along with the resultant warped signals, showing differences in assumptions of feature correspondence between the two methods.
2). Quantitative
We will show that the DTFM has a more consistent, predictable response to added signal noise than DTW. This gives DTFM the benefit of predictability — akin to the ℓ2-norm — while still being able to compare SCG signals with varying phase. To do so, we begin by representing the SCG signal as a windowed Fourier series. This offers a method of modeling signal noise as a linear combination of windowed sinusoids while still accurately modeling the SCG waveform.
Consider the template signal and raw signal defined along a time interval τ, which is divided into L non-overlapping, continuous windows such that . In this interval, t and s may be projected into Φ, the subspace of defined by the Fourier series:
| (7) |
where
| (8) |
Thus, any vector x ∈ Φ in interval τ can be expressed as:
| (9) |
where H is the maximum harmonic order and x is parameterized by . For simplicity, no offset term is included in the Fourier series, without loss of generality. In this study, both L and H are fixed to 8; that is, the signal is divided into 8 windows of length 100 ms, and the maximum sinusoidal frequency is 8 cycles per window. Note that this corresponds to a frequency range of 10Hz - 80Hz. Though in this study, SCG signals were low-pass filtered with a 40Hz cutoff, prior work has opted for cutoffs as high as 100Hz [12], [36]. These values of L and H were chosen to sufficiently illustrate patterns that span the typical SCG frequency spectrum.
Upon projecting t and s into Φ to obtain tΦ and sΦ respectively, the raw signal may be constructed by adding an error vector, also in Φ, to the template. Therefore, sΦ= tΦ + eΦ, where eΦ is an error vector in subspace Φ. As per (9), eΦ can be understood as a linear combination of windowed sinusoids added to the template to obtain the raw signal.
It is shown in Appendix A that the ℓ2-norm distance has the desirable property that noise components at different time windows and frequencies are equally-weighted in their contribution to overall distance. However, since DTW is not a linear operator, it does not share this property; rather, we will demonstrate experimentally that the DTW operator demonstrates time-frequency dependence. In contrast, we will also show that DTFM approximates the time-frequency independence of the ℓ2-norm, making it a more predictable method.
To model this dependence, 16 separate SCG templates were generated according to Algorithm 1, using data from the resting period of each of the 16 subjects in Protocol 1. These subject-specific templates were projected in to the subspace Φ such that each template was parameterized by coefficients θi, i ∈ [1, 16]. Synthetic signals were formed by first adding a random vector of error parameters θe to θi such that
| (10) |
Each element in θe was generated by a uniform distribution in range [0, 1]. The updated coefficients were then reconstructed using the Fourier series to obtain a synthetic signal as follows:
| (11) |
where is the Fourier series operator. After generating R = 160,000 synthetic signals (10,000 from each of the 16 templates), the parameterizations {θe}R for the synthetic signals were used to construct the row matrix where P is the number of parameters. These parameters were mapped to the corresponding distance between the synthetic signal and its respective template, given by . The mapping x is the least-squares estimate that satisfies
| (12) |
This mapping represents the contribution of each error parameter to the overall computed distance. After performing this method for both DTW and DTFM distance metrics, the coefficients in each window and frequency were averaged (corresponding to the sine and cosine components).
K. Evaluation of Ensemble Classifier
The classifier of Figure 3 was used to detect and localize sensor misplacement using the dataset from Protocol 2. This task was attempted in [18] using random forest classification on extracted features to detect, but not localize, SCG misplacement. Since the SCG sensor was placed in five different locations, this is a five-class classification problem. We denote these locations as C (center), L (left), R (right), T (top), and B (bottom). As described in [18], a sensor is misplaced whenever it is not located in C.
To demonstrate the performance of the classifier of Figure 3 on held-out subjects, we began by constructing 10 subject-specific template sets, one for each subject in Protocol 2. Each template set was composed of five templates, generated with Algorithm 1 from the subject’s resting-period segments from each of the five accelerometer positions. Note that because the center position in the protocol was tested on two separate days for each subject, data from both days was combined for template generation and validation. Thus, the template set for each subject S was . These template sets were then combined into a superset .
Next, the following was performed for each held-out subject S. A new superset MS was defined, composed of only held-in subjects, such that . To use this superset for classification purposes, we first characterized the prior distributions of each of the 9 held-in sets as per Equation 5. This distribution was modeled as a multivariate Gaussian such that the ith template set had a 5×5 matrix of means μi and one 5×5 covariance matrix per class . This setup is analagous to treating each set as a separate QDA classifier [29].
For each set in MS, these parameters were learned by obtaining the SQI for each template , j ∈ {C,L,R,T,B}, against all resting-period segments from held-in subjects using Equation 1. μi was then calculated as the mean score of each template for each class; each element in Σi was calculated as the covariance of SQIs between the five templates in for each class, respectively. Once the prior distributions were estimated, predictions were generated for all segments for subject S using superset MS as per Equation 6. This process was performed twice, once using DTW and once using DTFM as distance metrics. Note that because diversity in the model is driven by template variation, methods of selecting training data such as bagging and boosting were not used in this study. The prediction and target values for each subject were combined into a confusion matrix to show held-out predictive performance across the 10 subjects.
The nature of this task allows for multiple observations to be considered for each prediction. Intuitively, if the classifier predicts the correct location more often than any single incorrect location, incorporating more data into each decision increases the likelihood of correct prediction. Extending this intuition, given a column-normalized confusion matrix, where columns represent the true class and rows represent the predicted class, classification error will converge to 0 as datapoints per prediction increase if the mode of each column is located on the matrix diagonal.
To model this heuristic and determine the number of observations necessary to assure high performance, we upper-bound the probability of prediction error Pe given the confusion matrix of the classifier as a function of the number of observations per prediction B. Appendix B describes the formulation of this upper-bound, which will be used to evaluate the relative performance of each classifier.
Predictive performance was analyzed as a function of the number of template sets (n = [1, 9]) and number of signal segments per prediction (m = [1, 9]). The former was achieved by limiting the size of MS, selecting a random subset of size n on which to perform the analysis. The latter was achieved by selecting m segments at random from a random class for the held-out subject, predicting the class by returning the most common prediction over the m segments. For each subject, this process was performed 100 times for each of 81 pairs of values (m, n).
To compare results with [18], F1 scores were obtained for binary detection. Namely, the five-class problem was reduced to a two-class problem, where predictions and targets took the form C and , where . The F1 score was then calculated as
| (13) |
where P is precision, R is recall, TP are true positives, FP are false positives, and FN are false negatives. The F1 scores were calculated and recorded for each pair (m, n) across all trials and held-out subjects. The average F1 score was obtained for each pair (m, n) by averaging all recorded scores corresponding to each pair.
III. Results and Discussion
A. Qualitative Evaluation of DTFM and DTW
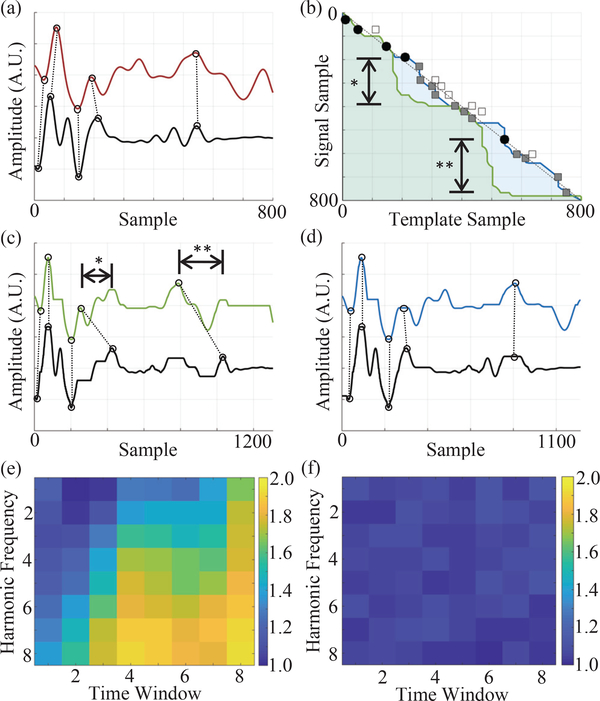
The time-warping results for a resting-period segment in Protocol 1 are shown in Figure 4(a)–(d). Most notably, there are two deviations in the DTW warp path — indicated with dimension lines in Figure 4(b) — that bring two major peaks of the SCG signal out of alignment with the template, as shown in Figure 4(c). DTW instead brings the original signal peaks into alignment with different peaks in the template, as this configuration minimizes the overall Euclidean distance. In contrast, restrictions on the DTFM warp path reduce the likelihood of peak misalignment by prioritizing feature matching over distance minimization. As shown in Figure 4(d), DTFM aligns corresponding peaks in the warped signal.
Fig. 4.
(a) Template signal (black) and raw signal (red) before warping. Five peaks from each signal that likely correspond were chosen by visual inspection and are connected by dashed lines. (b) Warping paths from DTW (green) and DTFM (blue) plotted against 1:1 correspondence line (black, dashed). Sub-optimal (square, empty) and optimal (square, shaded) candidate points are indicated, with the candidate points corresponding to the five features in (a) being indicated by black circles. (c) Template signal (black) and raw signal (green) after DTW. The new locations of the five corresponding points from (a) are connected by dashed lines. (d) Template signal (black) and raw signal (blue) after DTFM. The new locations of the five corresponding points from (a) are connected by dashed lines. Peak mismatches caused by DTW are indicated by the dimension lines in (b) and (c). Relative importance of noise components in predicting distance estimation by DTW (e) and DTFM (f). Harmonic frequency refers to the number of periods per window of the sinusoidal noise.
Notably, there are many restrictions that may be placed on the DTW warp path to reduce the likelihood of aberrant feature matching, including strictly limiting the acceptable warp path deviation from the straight-line fit. However, such restrictions in turn minimize the benefit of using DTW over simpler distance metrics such as the ℓ2-norm, as it decreases the ability of DTW to re-align off-set peaks. This property of DTW is essential when there is appreciable heart rate variability, as peak locations may shift with each subsequent sample. Besides requiring the warp path to match features whenever possible, no additional constraints are imposed by DTFM, maintaining the generalizability of the method.
B. Quantitative Evaluation of DTFM and DTW
The responses of DTFM and DTW to noise modeled as windowed sinusoids are shown in Figures 4(e) and (f). These signals were generated and analyzed using Equations 10–12. Note that these values were normalized by performing element-wise division of each point with the minimum value in the grid. Figure 4(e) demonstrates that the DTW distance is more sensitive to noise components at higher frequencies and at later intervals of the SCG signal. This is likely because most of the SCG signal energy is concentrated at lower frequencies early in the signal, corresponding to aortic opening (AO) and subsequent systolic ejection. Thus, noise in this region is less likely to encourage DTW to re-align peaks to minimize error. In contrast, Figure 4(f) shows that DTFM distance is equally affected by noise in any signal segment and at any frequency, much like the ℓ2-norm.
This property of DTW is undesirable in two ways. First, significant work in processing SCG signals focuses on AO point identification, but the effect of noise in this region on the SQI is relatively attenuated by DTW. Secondly, the response of DTW to signal noise is difficult to predict since the change in DTW distance with respect to individual noise components in non-uniform. In contrast, the response of DTFM to noise components is uniform, indicating that DTFM retains the predictability of the ℓ2-norm while having the additional benefit of aligning corresponding features.
C. Qualitative Evaluation of SQI
Selected segments from one of the subjects in Protocol 1 are shown in Figure 5(a). This result demonstrates that the SQI as defined in Equation 2 is able to identify high- and low- quality SCG segments when the subject is performing different activities. Compared to the top 2%, signals in the 50th percentile contain more noise in the first and second signal minima, which are often extracted as AO point correlates. Though there is no absolute reference standard for SCG, segments with higher SQI appear more uniform than those with lower SQI, and the high-energy oscillation in the first half of the signal — often associated with the AO point and systolic ejection — is more clearly distinguishable.
Fig. 5.
(a) Stratification of SCG signals using the DTFM-based SQI for a single subject. The columns from left to right show SCG intervals taken from rest, recovery, and exercise respectively. The top row corresponds to the top 2% of signals in each category based on their SQI; the middle rows correspond to the 50th percentile; and the bottom row corresponds to the bottom 2%. The correlation between scores assigned by manual annotation and the DTFM-based SQI are shown for the (b) rest, (c) recovery, (d) squatting, and (e) walking activity levels. The best-fit line for these scores is shown (black, dotted), with the corresponding R2 of the fit overlaid. For visual purposes, SQI scores were normalized to the range [0, 1].
This stratification of signal segments by SQI is an essential component of the overall QAM system. Improving stratification between activity levels better enables tailoring the quality threshold based on the tolerance of processing algorithms.
D. Quantitative Evaluation of SQI
Figure 5(b)–(d) show the relationship between DTFM-based SQI scores and those from visual manual annotation. Positive linear relationships are apparent at all activity levels, though this correlation is somewhat lower during walking. The results of this figure suggest that the heuristics by which human annotators scored the signal — including relative quality of features related to AO and AC — were reflected by the DTFM-based SQI. This follows intuition: since AO and AC generally yield high-energy features in the signal, distance minimization algorithms would incur a large penalty if these features were not identified and matched between the signal and template.
The ability of the different quality indexing methods to distinguish signals from different activity levels is shown in Figure 6(a). As shown in the figure, DTFM more effectively stratifies SCG segments taken during different activity levels based on their SQI compared to DTW. This is especially apparent between the rest and recovery periods, which DTW ranks as higher quality, in opposition to the visual scoring gold-standard. For this reason, the DTFM-based SQI produces a stratification that is more congruent with visual scoring.
Fig. 6.
(a) SQI scores for different activity levels using DTFM (blue) and DTW (green) as distance metrics and a template set size of 15. Scores from visual scoring with 10 annotators are included (red). Scores from each method were normalized to the range [0, 1] for comparison of score stratification. The boxes denote the 25th - 75th percentile range and the whiskers denote the 5th - 95th percentiles. (b) The test statistic from performing the Friedman test on template sets of increasing size for DTFM (blue) and DTW (green). Standard deviation error bars are shown. These are compared against the test statistic from visual scoring (red, dashed) with an increasing number of human annotators. (c) Pairwise test results versus number of template sets used. Categories include rest (Rs), recovery (Rc), squatting (S), and walking (W). Shading indicates statistically-significant separation (p <0.05) with DTFM (blue), DTW (green), or both (yellow) as determined by the Wilcoxon rank-sum test. These are compared against the pairwise results for visual scoring (red, dashed).
These results are reflected in Figure 6(b). Notably, all scoring methods produce test statistics which are relatively high compared to the chi-square critical value of 7.82 for 3 degrees of freedom. Since the relative value of the test statistic is due to differences in variance and not necessarily the validity of the scores assigned by each method, Figure 6(b) does not suggest that one method is better than the other. Rather, the result of interest is that, for DTFM-based SQI, increasing the number of reference templates or annotators increases score stratification. This suggests that, though there is no reference standard SCG, there are patterns on the population level which may be synthesized to effectively assess a signal. Furthermore, the relative separation when using DTFM increases compared to DTW as more templates are used, indicating that the addition of templates has a greater marginal benefit for DTFM.
Figure 6(c) shows the results of Wilcoxon rank-sum testing on the SQI scores across the four activity levels as the number of template sets is increased. Notably, using DTFM-based SQI typically requires fewer template sets to achieve significant separation between the pairs of activity levels compared to DTW. As expected from Figure 6(a), separating scores from rest and recovery periods was more difficult than distinguishing rest from exercise period scores for all methods, with visual scoring not achieving significant separation at all. DTW-based SQI and visual scoring were also unable to significantly distinguish signals captured from different exercise levels, though DTFM-based SQI achieved this with relatively few template sets. Though this does not serve as an indictment of DTW or visual scoring, it does suggest that DTFM may be a more appropriate SQI metric than DTW for identifying nuanced differences in the SCG signal, supporting the observations shown in Figure 7.
Fig. 7.
Confusion matrices for ensemble classification of signal misplacement using (a) DTW and (b) DTFM. Placement locations are center (C), left (L), right (R), top (T), and bottom (B). The matrices are column-normalized to highlight accuracy of predictions. The F1 scores for binary classification (center or off-center) using (c) DTW and (d) DTFM are shown below.
E. Evaluation of Ensemble Classifier
Performance of the ensembled QDA classifier for SCG misplacement detection is shown in Figure 7. Notably, the DTW-based classifiers had lower performance in correctly classifying centrally-placed SCG sensors, leading to lower precision in detection. This is likely due to the fact that, for each subject, data for centrally-placed sensors was taken across two separate days, as opposed to the other locations which were obtained on a single day. This introduced variability in sensor placement — and possibly the subject’s physiological state — within the class. In contrast to DTW, DTFM-based classifiers were better able to handle this variability.
SCG waveforms are, by nature, both transient and subject-specific. This means that, across patients and across recording sessions, subjects’ baseline SCG morphology may change. Performing held-out cross validation addresses this factor; with this method, predictions of sensor position did not incorporate knowledge of the subjects’ baseline, prototypical SCG waveform. An implication of these results is that, even with such diverse waveforms in the training set, stereotyped changes in morphology existed with each sensor position.
Figures 7(c) and (d) show the F1 scores for misplacement detection as a function of the number of template sets used by the classifier and number of SCG segments used for each prediction. For DTFM-based classifiers, performance improved with more template sets and segments per prediction. The former is because, as previously demonstrated, SQI performance generally improves with the number of reference templates; the latter is because, as long as the classifier predicts the correct location more often than any single incorrect location, incorporating more data into each prediction increases the likelihood of correct prediction. Performing the analysis from Equation 20 on the confusion matrices of Figure 7(a) and (b) yields the results in Figure 8. Since the probability of prediction error for DTW is bounded away from 0 due to misclassification of centrally-placed SCGs, overall performance does not improve despite improvements when predicting the remaining classes.
Fig. 8.
Probability of prediction error given the confusion matrices in Figure 7 (a) and (b). The error probability using the DTW distance metric is shown in green, with the shaded area representing the error range across all sensor locations and green lines representing the error for individual locations. The error probability using DTFM is shown in blue, with the shaded area representing the error range and blue lines showing location-specific error. The black dotted lines correspond to the mean error probability across locations. The outlier green line is associated with detection of correct sensor placement.
The error-bounding of Figure 8 is significant because the use-case of misplacement detection allows for the assumption that more than one segment may be used per prediction. Thus, if the confusion matrix for a given classifier is generalizable to held-out subjects, one may obtain a reasonable upper-bounded prediction error for each class, using this to determine how many segments to obtain. For binary classification, DTFM-based classifiers achieved an F1 score of 0.83; these results are comparable to the F1 score of 0.82 achieved in [18] for the same task, though held-out validation was not used in [18]. Furthermore, these results extend prior work by demonstrating the ability to localize SCG misplacement as well, with diminishing error.
IV. Conclusion and Future Work
In this work, we proposed a method of SCG signal quality assurance based on quality indexing and classification. By using population-based methods, these tasks were accomplished despite having no standard baseline for SCG. Furthermore, the fact that the results of this study were obtained using held-out validation has significant implications for using the proposed QAM in ambulatory environments where there may not be an opportunity for subject-specific sensor calibration, or on low-power devices where such learning is not possible.
Notably, the SQI and ensemble classifier presented in this work derive from a unified method. Namely, the SQI of Equation 2 can be viewed as a special case of the ensemble classifier of Figure 3, where each template set contains a single resting-period template and the mean SQI is returned as a result. Unification of the traditionally disparate tasks of quality indexing and signal classification is a key result of this work.
A driving force in biomedical informatics is the use of feature-mining coupled with often highly-nonlinear models to perform classification and regression tasks. For instance [18] extracted 26 signal features coupled with XGBoost classification to perform SCG misplacement detection. In this work, the SQI is used as the sole feature type in a linear QDA classifier, yielding a method that is effective for this task while remaining intuitive and interpretable. This result is essential because it not only illustrates the broader potential of the SQI but also demonstrates that robustness and interpretability are not necessarily incongruent. For informatics as a whole, developing intuitive and interpretive models as opposed to black-box systems is an important component in the eventual acceptance of these models by the medical community.
Finally, an important implication of this work is the observation of population-level behavior of SCG morphology. While the SCG is considered both patient-specific and transient, the ability to classify sensor placement without user calibration suggests that there exist high-level patterns in these waveforms despite their stochastic nature. Future work should explore this result, as it may eventually lead to more robust and generalizable methods of analysis.
Regarding SQI assessment, this study only explored four noise levels; to further validate generalizability of this method, more noise levels should be tested, namely those encountered in outpatient monitoring scenarios, for example noise due to clothing interference, speaking, and upper body movements. For sensor misplacement, the dataset used in this study featured larger displacements (5–7.5cm) than may typically be encountered in at-home settings, and only tested the four cardinal directions. Future work should demonstrate the efficacy of this method for more minute displacements and in different directions. A key limitation of the ensemble classifier is that misplacement is detected only during the resting period. While held-out validation shows that this approach generalizes well, classification during the resting period only is a limitation compared to prior work. Future work should build on these results by validating this classification method against other source distributions of interest in SCG processing.
ACKNOWLEDGMENT
We would like to thank Dr. Hazar Ashouri for her work in collecting and making available the data used in this study regarding SCG sensor misplacement.
This material is based on work supported by the National Institutes of Health under Grant 1R01HL130619-A1 and the National Center for Advancing Translational Sciences of the National Institutes of Health under Award Number UL1TR002378.
Appendix A
Proof of Time-Frequency Independence of ℓ2-norm
Consider the functions and defined as where and where c, d ∈ Φ, the subspace defined by the Fourier series. The true ℓ2-norm η* between the template t and raw signal s can thus be found as
| (14) |
The true distance between the vectors may be estimated by finding the ℓ2-norm of the projections in Φ of the template and raw signal.
| (15) |
It can be shown that and η* converge as the order number H is increased. Since the norm operator is linearly separable for orthogonal vectors, the estimated norm may be expressed as the sum of its individual components.
| (16) |
where 0Φ is the zero vector in Φ and eΦ is the difference between the raw signal and template. This shows that the ℓ2-norm can be expressed as an unweighted sum of individual noise components at each time-window and frequency.
Appendix B
Derivation of Upper-Bound for Prediction Error
Consider a column-normalized confusion matrix , where each column represents the true class and each row represents the predicted class. Thus, each element in C represents the probability pij of predicting class i when the true class is j. Assuming all classes are equally likely to occur, we express the probability of prediction error as
| (17) |
where X is the predicted class and Y is the true class. This is the probability that the predicted class is different than the true class. Since the final prediction is defined as the mode of predictions on each batch of observations, an error occurs if any false class iis predicted more than any of the other classes. In other words,
| (18) |
where Sij(B) is the number of times the event X = i, Y= j occurs over the course of B observations. This is an upper-bound because the constraint that the number of observed events must total B has been lifted. We further simplify this expression by noting that each term in the product has a value in [0,1]. By definition, the result can never exceed the smallest term in the product. In this case, the smallest term in the product is where . Thus, we further upper-bound the probability of error by
| (19) |
Finally, we observe that the probability of selecting a certain class k times across B observations can be modeled as a binomial distribution parameterized by the probability of selecting the class X given the true class Y. We thus replace the probability terms in the previous equation with the binomial probability density function:
| (20) |
where β(k,B,p) is the binomial PDF evaluated at k event occurrences over B observations with event probability p, and .
REFERENCES
- [1].Inan OT, Migeotte PF, Park KS, Etemadi M, Tavakolian K, Casanella R, Zanetti J, Tank J, Funtova I, Prisk GK, and Di Rienzo M, “Ballistocardiography and seismocardiography: a review of recent advances,” IEEE J Biomed Health Inform, vol. 19, no. 4, pp. 1414–27, 2015. [DOI] [PubMed] [Google Scholar]
- [2].Crow R, Hannan PJ, Jr DRJ, Hedquist L, and Salerno D, “Relationship between seismocardiogram and echocardiogram for events in the cardiac cycle,” American Journal of Noninvasive Cardiology, vol. 8, no. 1, pp. 39–46, 1994. [Google Scholar]
- [3].Gurev V, Tavakolian K, Constantino J, Kaminska B, Blaber AP, and Trayanova NA, “Mechanisms underlying isovolumetric contraction and ejection peaks in seismocardiogram morphology,” Journal of Medical and Biological Engineering, vol. 32, no. 2, pp. 103–110, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Zanetti JM and Tavakolian K, “Seismocardiography: Past, present and future,” in 2013 35th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC) IEEE, 2013, pp. 7004–7007. [DOI] [PubMed] [Google Scholar]
- [5].Inan OT, Baran Pouyan M, Javaid AQ, Dowling S, Etemadi M, Dorier A, Heller JA, Bicen AO, Roy S, De Marco T, and Klein L, “Novel wearable seismocardiography and machine learning algorithms can assess clinical status of heart failure patients,” Circ Heart Fail, vol. 11, no. 1, p. e004313, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Di Rienzo M, Vaini E, Castiglioni P, Merati G, Meriggi P, Parati G, Faini A, and Rizzo F, “Wearable seismocardiography: towards a beat-by-beat assessment of cardiac mechanics in ambulant subjects,” Autonomic Neuroscience, vol. 178, pp. 50–59, 2013. [DOI] [PubMed] [Google Scholar]
- [7].Taebi A, Solar B, Bomar A, Sandler R, and Mansy H, “Recent advances in seismocardiography,” Vibration, vol. 2, no. 1, pp. 64–86, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Khosrow-Khavar F, Tavakolian K, Blaber A, and Menon C, “Automatic and robust delineation of the fiducial points of the seismocardiogram signal for non-invasive estimation of cardiac time intervals,” IEEE Trans Biomed Eng, vol. 64, no. 8, pp. 1701–1710, 2017. [DOI] [PubMed] [Google Scholar]
- [9].Zakeri V, Khosrow-Khavar F, and Tavakolian K, “Automatic detection of low-quality seismocardiogram cycles using the outlier approach,” in World Congress on Medical Physics and Biomedical Engineering, June 7–12, 2015, Toronto, Canada: Springer, 2015, pp. 1014–1017. [Google Scholar]
- [10].Sahoo PK, Thakkar HK, Lin WY, Chang PC, and Lee MY, “On the design of an efficient cardiac health monitoring system through combined analysis of ecg and scg signals,” Sensors, vol. 18, no. 2, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Jain PK, Tiwari AK, and Chourasia VS, “Performance analysis of seismocardiography for heart sound signal recording in noisy scenarios,” J Med Eng Technol, vol. 40, no. 3, pp. 106–18, 2016. [DOI] [PubMed] [Google Scholar]
- [12].Taebi A and Mansy HA, “Time-frequency distribution of seismocardiographic signals: A comparative study,” Bioengineering (Basel), vol. 4, no. 2, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Javaid AQ, Ashouri H, Dorier A, Etemadi M, Heller JA, Roy S, and Inan OT, “Quantifying and reducing motion artifacts in wearable seismocardiogram measurements during walking to assess left ventricular health,” IEEE Transactions on Biomedical Engineering, vol. 64, no. 6, pp. 1277–1286, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].Yang C and Tavassolian N, “Combined seismo- and gyro-cardiography: A more comprehensive evaluation of heart-induced chest vibrations,” IEEE Journal of Biomedical and Health Informatics, vol. 22, no. 5, pp. 1466–1475, 2018. [DOI] [PubMed] [Google Scholar]
- [15].Luu L and Anh D, “Artifact noise removal techniques on seismocardiogram using two tri-axial accelerometers,” Sensors, vol. 18, no. 4, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16].Shandhi MMH, Semiz B, Hersek S, Goller N, Ayazi F, and Inan O, “Performance analysis of gyroscope and accelerometer sensors for seismocardiography-based wearable pre-ejection period estimation,” IEEE J Biomed Health Inform, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17].Tadi MJ, Lehtonen E, Saraste A, Tuominen J, Koskinen J, Teräs M, Airaksinen J, Pankäälä M, and Koivisto T, “Gyrocardiography: A new¨ non-invasive monitoring method for the assessment of cardiac mechanics and the estimation of hemodynamic variables,” Scientific reports, vol. 7, no. 1, p. 6823, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].Ashouri H and Inan OT, “Automatic detection of seismocardiogram sensor misplacement for robust pre-ejection period estimation in unsupervised settings,” IEEE Sensors Journal, vol. 17, no. 12, pp. 3805–3813, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19].Woody CD, “Characteristics of an adaptive filler for the analysis of variable latency neuroelectric signals,” Medical and Biological Engineering and Computing, vol. 5, no. 6, pp. 539–554, 1967. [Google Scholar]
- [20].Berndt DJ and Clifford J, “Using dynamic time warping to find patterns in time series” in KDD workshop, vol. 10, no. 16. Seattle, WA, 1994, pp. 359–370. [Google Scholar]
- [21].Huang B and Kinsner W, “Ecg frame classification using dynamic time warping,” in IEEE CCECE 2002. Canadian Conference on Electrical and Computer Engineering, vol. 2 IEEE, 2002, pp. 1105–1110. [Google Scholar]
- [22].Raghavendra B, Bera D, Bopardikar AS, and Narayanan R, “Cardiac arrhythmia detection using dynamic time warping of ecg beats in ehealthcare systems,” in 2011 IEEE International Symposium on a World of Wireless, Mobile and Multimedia Networks. IEEE, 2011, pp. 1–6. [Google Scholar]
- [23].Li Q and Clifford GD, “Dynamic time warping and machine learning for signal quality assessment of pulsatile signals,” Physiological Measurement, vol. 33, no. 9, pp. 1491–1501, 2012. [DOI] [PubMed] [Google Scholar]
- [24].Boulgouris NV, Plataniotis KN, and Hatzinakos D, “Gait recognition using dynamic time warping,” in IEEE 6th Workshop on Multimedia Signal Processing, 2004. IEEE, 2004, pp. 263–266. [Google Scholar]
- [25].Corradini A, “Dynamic time warping for off-line recognition of a small gesture vocabulary,” in Proceedings IEEE ICCV workshop on recognition, analysis, and tracking of faces and gestures in real-time systems. IEEE, 2001, pp. 82–89. [Google Scholar]
- [26].Senin P, “Dynamic time warping algorithm review,” Information and Computer Science Department University of Hawaii at Manoa Honolulu, USA, vol. 855, pp. 1–23, 2008. [Google Scholar]
- [27].Keogh E and Ratanamahatana CA, “Exact indexing of dynamic time warping,” Knowledge and Information Systems, vol. 7, no. 3, pp. 358–386, 2005. [Google Scholar]
- [28].Vincent WJ and Weir JP, Statistics in Kinesiology, 4th ed. Human Kinetics, 2012. [Google Scholar]
- [29].Hastie T, Tibshirani R, and Friedman J, The Elements of Statistical Learning, 2nd ed. Springer, 2009. [Google Scholar]
- [30].Polikar R, “Ensemble based systems in decision making,” IEEE Circuits and Systems Magazine, pp. 21–45, 2006. [Google Scholar]
- [31].Romero D, Calvo M, Béhar N, Mabo P, and Hernández A, “Ensemble classifier based on linear discriminant analysis for distinguishing brugada syndrome patients according to symptomatology,” in 2016 Computing in Cardiology Conference (CinC) IEEE, 2016, pp. 205–208. [Google Scholar]
- [32].Ozcift A, “Random forests ensemble classifier trained with data resampling strategy to improve cardiac arrhythmia diagnosis,” Computers in Biology and Medicine, vol. 41, no. 5, pp. 265–271, 2011. [DOI] [PubMed] [Google Scholar]
- [33].Plawiak P, “Novel genetic ensembles of classifiers applied to myocardium dysfunction recognition based on ecg signals,” Swarm and Evolutionary Computation, vol. 39, pp. 192–208, 2018. [Google Scholar]
- [34].Das R, Turkoglu I, and Sengur A, “Effective diagnosis of heart disease through neural networks ensembles,” Expert Systems with Applications, vol. 36, no. 4, pp. 7675–7680, 2009. [DOI] [PubMed] [Google Scholar]
- [35].Hong S, Wu M, Zhou Y, Wang Q, Shang J, Li H, and Xie J, “Encase: An ensemble classifier for ecg classification using expert features and deep neural networks,” in 2017 Computing in Cardiology (CinC). IEEE, 2017, pp. 1–4. [Google Scholar]
- [36].Pandia K, Inan OT, and Kovacs GTA, “A frequency domain analysis of respiratory variations in the seismocardiogram signal,” in IEEE EMBC 2013. IEEE Engineering in Medicine and Biology Society Conference IEEE, 2013, pp. 6881–6884. [DOI] [PubMed] [Google Scholar]