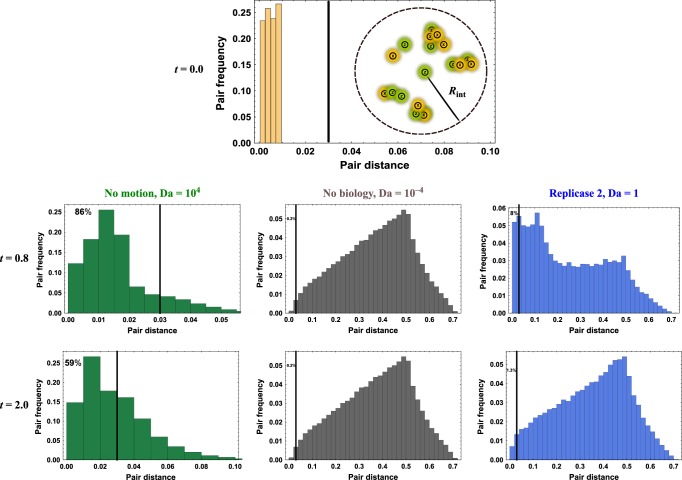
Fig. 3. The relative value of the fluid velocity and metabolic timescales is critical for cooperation.

The importance of the Damköhler number, and of flows in general, can be understood via the pair covariance G(|x₁ − x₂|), which gives the probability of finding a pair with interparticle separation |x₁ − x₂|. Starting from an initial condition of many particles in close proximity (so G(|x₁ − x₂|) can be approximated by a delta function at G(0)), the evolution of pair covariance is governed by competition between flow and biology. Histograms show an average over 1000 simulations. Times are measured in the expected lifetime of a single biological particle. When particles reproduce, we use the interaction radius R_int = 0.03, and the fraction of interacting particles (left of black bar) is given at the top-left. In the absence of flow (green histograms), the initial condition will slowly spread into a large colony, with most particles within the interaction radius, leaving the susceptible to parasites. On the other hand, passive tracers in a turbulent flow (gray histograms) obey a known power law⁸⁴, in which the interparticle distance increases on average, here quickly reaching a limiting distribution due to the doubly periodic nature of our spatial domain. In this situation, so few pairs are within the interaction radius that most lineages should be expected to die out and the population on average goes extinct. A replicating population in a flow at $Da=\mathcal{O}\left(1\right)$ (blue histogram), however, can combine the advantages of both situations, creating rich structure (G(x₁, x₂) having broad support) while also having a higher number of interacting pairs than in the case of no biology.