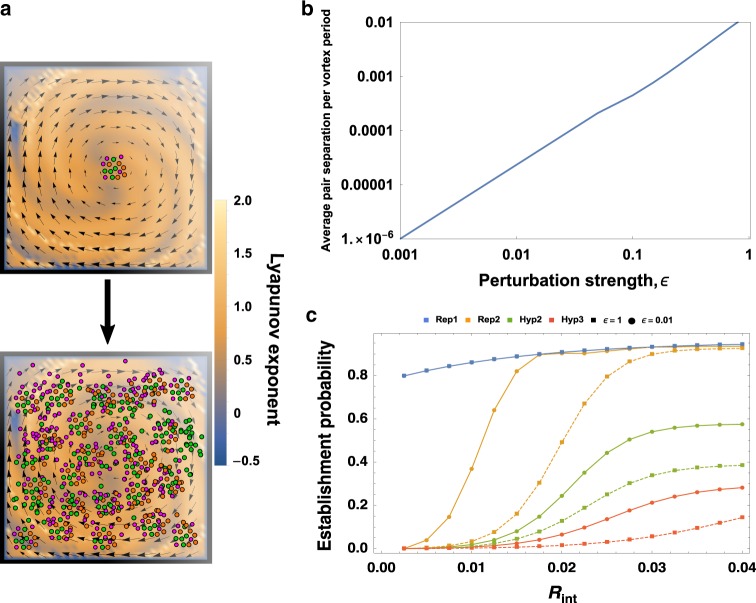
Fig. 4. Coherent structures collocalize replicating particles.
a A sample velocity field consisting of a circular flow perturbed by an unsteady oscillation of amplitude ε = 0.1 atop a plot of the finite-time Lyapunov exponent, a common measure of the local “chaoticity” in a flow. As ε increases, particles (colored dots, schematizing different species) become more likely to cross onto the unstable manifold and separate from nearby neighbors. We define “establishment” as a hundredfold increase in the population size starting from a very small initial condition, where continuum limits previously described32,33,36 begin to be applicable. b The average particle separation (per flow period) of an initially adjacent pair of particles, versus the strength ε of the perturbation, in logarithmic scale. c Results of numerical simulations of various metabolisms (colors) for varying distances Rint at which particles can cooperate with one another. Square markers indicate the likelihood that the population increases 1000-fold starting from an inoculum of five particles of each species injected into a chaotic field (no coherent structure, ε = 1), whereas circular markers indicate the same likelihood for an identical inoculum injected into a nearly pure coherent structure (ε = 0.01). Note that for Replicase R1 (blue), the establishment probability is equal for both ε = 1 and ε = 0.01, so that only the solid line is shown.