TABLE 1:

Traditional critical concentration definitions used in the literature.

Classical CC definition	Abbreviation	Experimental measurement of CC as applied to MT systems
Minimal concentration of total subunits (e.g., tubulin dimers) necessary for polymer assembly ( Oosawa, 1970; Johnson and Borisy, 1975)	CCPolAssem	CCPolAssem is determined by measuring steady-state [polymerized tubulin] at different [total tubulin] in a competing system and extrapolating back to [polymerized tubulin] = 0. See Q1 in Figure 1A (also Figures 3, A and B, and 4).
Concentration of free subunits left in solution once equilibrium or steady-state assembly has been achieved ( Oosawa, 1970; Johnson and Borisy, 1975)a	CCSubSoln	CCSubSoln is determined by measuring [free tubulin] left in solution at steady state for different [total tubulin] in a competing system and determining the position of the plateau reached by [free tubulin]. See Q2 in Figure 1A (also Figures 3, A and B, and 4).
Dissociation equilibrium constant for the binding of subunit to polymer, i.e., CC = KD = koff/kon ( Oosawa and Asakura, 1975)b	CCKD	CCKD can be determined by separate experimental measurement of kon and koff for addition/loss of tubulin subunits to/from MT polymer, respectively, and then calculating the ratio koff/kon.
Concentration of free subunit at which the rate of association equals the rate of dissociation during the elongation phase (called Sce in Walker et al., 1988; similar to c1 in Hill and Chen, 1984)c	CCElongation	CCElongation is determined by measuring the growth rate during the growth state (Vg) at various values of [free tubulin] and extrapolating back to the [free tubulin] at which Vg = 0. See Q3 in Figure 1B (also Figure 7, A and B).
Concentration of free subunit at which the fluxes of subunits into and out of polymer are balanced, that is, where the net flux is zero (called c0 in Hill and Chen, 1984)	CCFlux	CCFlux is determined by growing MTs to steady state at very high [total tubulin], then rapidly diluting to a new [free tubulin] and measuring the initial rate of change in [polymerized tubulin] (i.e., measuring [polymerized tubulin] flux). CCFlux is the value of [free tubulin] where [polymerized tubulin] flux = 0. See Q4 in Figure 1C (also Figure 6).
Concentration of free subunit at which polymers transition from “bounded growth” to “unbounded growth” (called ccr in Dogterom and Leibler, 1993)	CCUnbounded	CCUnbounded is the [free tubulin] at which the rate of change in average MT length transitions from equaling zero to being positive (Q5 in Figure 5). CCUnbounded can be identified by measuring DI parameters from MT length histories (Figure 1, E and F) across a range of different [free tubulin] and determining the [free tubulin] at which VgFres = |Vs|Fcat.

These definitions of CC are interchangeable for equilibrium polymers, but have not all been compared in a single analysis for DI polymers. For each CC definition, we have assigned a specific abbreviation and provided an example of an early publication where that definition was used. The terms CC_PolAssem, CC_SubSoln, etc., refer to theoretical values (concepts), and Q1, Q2, etc., refer to experimentally measurable quantities (i.e., values obtained through experimental approaches as indicated in the figures). All definitions except CC_KD can be applied to both equilibrium and steady-state polymers (CC_KD assumes that the system is at equilibrium and therefore can be applied to only equilibrium polymers). The traditional framework outlined here will be revised in Results, where we will show that these definitions are not all equivalent for DI polymers (see Tables 3 and 4 for a summary).

^aAssuming that assembly starts from a state with no polymer, maximal polymer assembly will occur at equilibrium for equilibrium polymers, and at polymer-mass steady state for steady-state polymers. Steady-state polymers will be (mostly) disassembled at thermodynamic equilibrium because the nucleotides in the system will be (effectively) entirely hydrolyzed.

^bThe idea that CC = K_D for simple equilibrium polymers is derived as follows. The net rate of polymer length change at a single filament tip = rate of addition – rate of loss. The rate of addition is assumed to be k_on[free subunit], and the rate of loss is assumed to be k_off. Therefore, the rate at which new subunits add to a population of n polymers is n × k_on[free subunit], and the rate at which subunits detach from a population of n polymers is n × k_off. At equilibrium, rate of polymerization = rate of depolymerization, so n × k_on[free subunit] = n × k_{off .} Therefore, at equilibrium, [free subunit] = k_off/k_on = K_D = CC_KD.

^cCC_Elongation has been interpreted as the minimal concentration of free subunit needed to elongate from a growing polymer. The derivation of CC_Elongation is similar to that for CC_KD, but considers the behavior of a single filament, not a population, and can apply to steady-state polymers because it does not require equilibrium. For polymers displaying DI, measurements of CC_Elongation are performed during the growth state of DI. The derivation of CC_Elongation assumes that V_g is a linear function of [free subunit], i.e., , where and are observed rate constants during growth. Thus, the [free subunit] at which V_g = 0 is 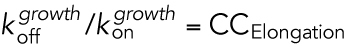.