Abstract
Multivariate Hawkes processes (MHPs) are a class of point processes where an arrival in one dimension can affect the future arrivals in all dimensions. Existing MHPs are associated with homogeneous link functions. However, in reality, different dimensions may exhibit different temporal characteristics. In this paper, we augment MHPs by incorporating heterogeneous link functions, referred to as hybrid MHPs, to capture the temporal characteristics in different dimensions. Since the branching structure can be utilized to equivalently represent MHPs, we propose a novel model called BRUNCH via intensity-driven Chinese Restaurant Processes (intCRP) to identify the optimal branching structure of hybrid MHPs. Furthermore, we relax the constraint on the shapes of triggering kernels in MHPs. We develop a Monte Carlo-based inference algorithm called MEDIA to infer the branching structure. Experiments on real-world datasets demonstrate the superior performance of BRUNCH and its usefulness in social media applications.
Keywords: Branching structure, Hawkes process, Heterogeneous link functions, Social media
Introduction
Multivariate Hawkes processes (MHPs) are a class of point processes with mutually exciting components to model sequences of discrete events in continuous time, where an arrival in one dimension can affect future arrivals in all dimensions [5, 6]. Recently, MHPs have emerged in multiple fields to capture mutual excitation between dimensions, including high frequency trading [1], social influence analysis [16] and computational biology [13]. However, these MHPs are limited to a specific scenario where a past arrival can only excite the occurrence of future arrivals, and the corresponding link functions1 are linear (i.e., linear MHPs). However, in reality, inhibitory arrivals and non-additive aggregation of effects from past arrivals are present in several application domains [10]. For instance, negative feedbacks of online consumers may inhibit others’ purchasing behaviours. Consequently, MHPs associated with nonlinear link functions, namely nonlinear MHPs [10], have been proposed where effects from past events encompass both excitation and inhibition.
Prior work on MHPs also assume that all dimensions take the same link function i.e., either linear or nonlinear MHPs (homogeneous MHPs). That is, all dimensions follow roughly the same temporal characteristics. Note that a dimension may record actions of a user (e.g., tweet, retweet, comment, share) in social media, behavior of a customer (e.g., purchase, comment, return) in online shopping websites, and so on. In reality, different dimensions may exhibit different temporal characteristics. For example, in Twitter, one individual (i.e., dimension) may be extremely interested in a popular topic and interact with her followers frequently whereas another individual may take little interest in that topic and seldom respond to his followers. In such scenario, the cumulative influence from recent events on the former individual is clearly different from the one on the latter. Hence, homogeneous MHPs are insufficient to capture such diverse temporal characteristics. To address this problem, in this paper we augment MHPs by incorporating heterogeneous link functions, referred to as hybrid MHPs, allowing us to cope with diverse impact of past events on future events in different dimensions.
The cluster Poisson process interpretation [7] of MHPs separates the events into two categories, namely, immigrants and offspring. The offspring events are triggered by past events, while the immigrants arrive independently and thus do not have a existing parent event. Offsprings are structured into clusters associated with each immigrant event. This is called the branching structure [8], which is an useful representation of MHPs in various applications. For example, in social influence analysis it can construct the narrative of information diffusion to pave the way for strategies to encourage or limit individual behaviors [14]. Additionally, the branching structure is widely utilized as a strategy in the maximum likelihood estimation of MHPs [16]. Unfortunately, such cluster Poisson process representation can only be applied to linear MHPs due to the mutually exciting assumption. Nonlinear MHPs cover both mutual excitation and mutual inhibition stochastically. Consequently, existing approaches based on the cluster Poisson process representation cannot be adopted to infer the branching structure of hybrid MHPs. In this paper, we infer the branching structure of hybrid MHPs regardless of the shapes of the triggering kernel functions2.
We propose a novel probabilistic model called BRUNCH (Branching stRUcture iNferenCe of Hybrid multivariate Hawkes processes) to reveal the branching structure of hybrid MHPs without assuming homogeneity of link functions or shapes of triggering kernel functions (Sect. 3). It is important for our probabilistic model to emphasize the following two features mirrored by the event sequences in MHPs: (a) the chronological order of events is nonexchangeable; and (b) the triggering relations could distribute within or across dimensions stochastically. To this end, we propose intensity-driven Chinese Restaurant Process (intCRP), a novel extension of classical CRP [3] in which the random seating assignment of the customers depends on the triggering kernels between them. In particular, intCRP has a nested structure – inner intCRP to explore the possible triggering relations among events occurring in one dimension (i.e., event links), and outer intCRP to identify the collection of triggering relations between all events and their parents (if any) across dimensions (i.e., cluster links). Obviously, the changes to the triggering relations within and across dimensions are highly coupled, i.e., the inner intCRP and outer outCRP are strongly interlaced. Since there are countably infinite sets of triggering relations, we propose a novel inference approach called MEDIA (MontE Carlo-baseD Inference Approach) that leverages the triggering nature of MHPs to sample event links and cluster links alternatively (Sect. 4). Finally, we apply BRUNCH on real-world social media datasets, and the experimental study in Sect. 5 demonstrates its superior performance and usefulness. Formal algorithms and proofs of theorems and lemmas appear in [9]. List of key symbols used in this paper is given in Table 1.
Table 1.
Key notations.
| Notation | Definition | Notation | Definition |
|---|---|---|---|
 |
Event sequences |  |
k-th arrival in i-th dimension |
 |
i-th event sequence |  |
Event number until t in i-th dimension |
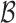 |
Collection of event links |  |
Event link from event  to event to event 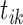
|
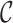 |
Collection of cluster links | 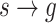 |
Cluster link from cluster s to cluster g |
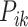 |
Events triggered by 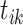
|
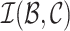 |
Collection of cascades |
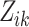 |
Parent event of 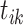
|
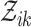 |
The cascade the event 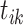 belongs to belongs to |
Preliminaries
In this section, we introduce relevant concepts for understanding this paper.
Multivariate Hawkes Processes (MHPs)
The conditional intensity function of the i-th dimension for an M-dimensional MHP takes the following form [10]:
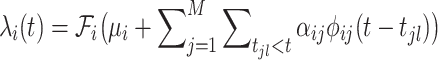 |
2.1 |
where 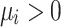 is the base intensity capturing the arrival rate of exogenous events independent of historical events. The term
is the base intensity capturing the arrival rate of exogenous events independent of historical events. The term  represents the accumulation of endogenous intensity caused by history [4]. The coefficient
represents the accumulation of endogenous intensity caused by history [4]. The coefficient 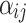 measures the influence from the j-th dimension to the i-th dimension, allowing mutual excitation (
measures the influence from the j-th dimension to the i-th dimension, allowing mutual excitation (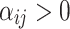 ) and mutual inhibition (
) and mutual inhibition ( ). The triggering kernel function
). The triggering kernel function
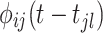 quantifies the triggering effect from the event
quantifies the triggering effect from the event 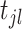 (i.e.,
(i.e.,
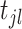 denotes the l-th arrival occurring in the j-th dimension) to the occurrence rate of the i-th dimension. Most of the existing work use predefined kernel functions with unknown parameters, such as the exponential kernels [16] and the power-law kernels [15]. The link function
denotes the l-th arrival occurring in the j-th dimension) to the occurrence rate of the i-th dimension. Most of the existing work use predefined kernel functions with unknown parameters, such as the exponential kernels [16] and the power-law kernels [15]. The link function
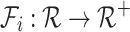 , recognizes the triggering pattern of the i-th dimension over the historical events. The linear MHPs [6] is the case
, recognizes the triggering pattern of the i-th dimension over the historical events. The linear MHPs [6] is the case 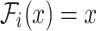 with nonnegative
with nonnegative 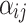 for each dimension, while nonlinear MHPs apply various
for each dimension, while nonlinear MHPs apply various 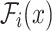 to guarantee the positive intensities. In hybrid MHPs, we allow each dimension to take a personalized link function to capture diverse temporal characteristics in real-world scenarios.
to guarantee the positive intensities. In hybrid MHPs, we allow each dimension to take a personalized link function to capture diverse temporal characteristics in real-world scenarios.
Branching Structure
Recall that the events in MHPs are classified as either immigrants or offsprings. An immigrant event arrives independently of other events, while an offspring event is triggered by a previous event. In the sequel, we refer to an immigrant together with its offsprings as a cascade. The collection of triggering relations in cascades is called the branching structure [8]. The cluster Poisson processes [7] could equivalently represent the branching structure of linear MHPs. Briefly, each immigrant starts one cascade, which consists of offspring events of the 1 , 2
, 2 , 3
, 3 ,
, 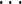 generations, controlled by the endogenous intensity in Eq. 2.1 [11]. Due to the non-linear link functions, the above branching structure representation based on the cluster Poisson processes is inapplicable for nonlinear MHPs and hybrid MHPs.
generations, controlled by the endogenous intensity in Eq. 2.1 [11]. Due to the non-linear link functions, the above branching structure representation based on the cluster Poisson processes is inapplicable for nonlinear MHPs and hybrid MHPs.
Suppose that 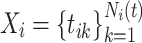 denotes the i-th event sequence during a time window [0, t]. Then
denotes the i-th event sequence during a time window [0, t]. Then 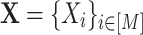 is the collection of events from M dimensions during [0, t]. While modeling the sequences
is the collection of events from M dimensions during [0, t]. While modeling the sequences 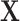 via hybrid MHPs, the corresponding branching structure could be represented by the variable set
via hybrid MHPs, the corresponding branching structure could be represented by the variable set 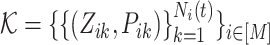 mathematically, such that
mathematically, such that
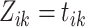 if
if 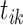 is an immigrant; and
is an immigrant; and 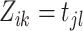 if event
if event 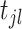 triggers
triggers 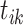 ; and
; and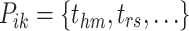 if there are some events
if there are some events 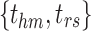 triggered by
triggered by 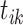 ; otherwise,
; otherwise, 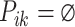 .
.
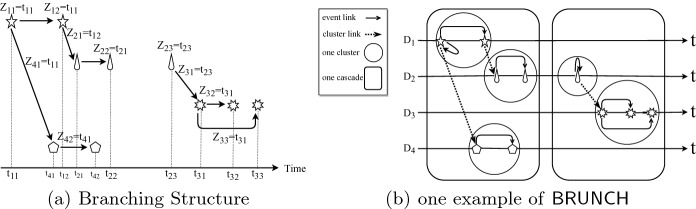
Our objective is to infer 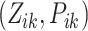 for each event. Consider Fig. 1(a). Directed links sketch an example of branching structure.
for each event. Consider Fig. 1(a). Directed links sketch an example of branching structure. 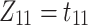 indicates the event
indicates the event 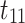 is an immigrant, and
is an immigrant, and 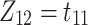 shows
shows 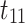 triggers
triggers 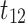 .
.  and
and 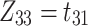 leads to
leads to 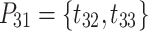 , denoting that
, denoting that  triggers
triggers 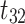 and
and 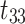 successively.
successively.
Fig. 1.
(a) An example of branching structure of MHPs and the events on the time axis; (b) Branching structure construction using BRUNCH.
The BRUNCH Model
While modeling the asynchronous time-stamped event sequences via hybrid MHPs, we aim to reveal the underlying branching structure. Although the traditional Chinese Restaurant Process (CRP) [3] provides a flexible class of distributions that is amenable for modeling dependencies between elements, the exchangeability assumption here is problematic for elements with temporal dependencies. This is because events in MHPs occur at different time points, and are nonexchangeable. In addition, in our problem setting the influence that determines the pairwise dependencies between events is not homogeneous within and across different sequences. Intuitively, it is natural to quantify the influence via the triggering kernels in Eq. 2.1. In order to tackle these issues, we present the BRUNCH model, which is based on intensity-driven Chinese restaurant processes (intCRP), a new variant of CRP that allows a number of intensity-driven distributions as priors on triggering relations between events.
The events in one cascade could stem from different dimensions. So, beyond the triggering relations obtained from single-sequence intCRP, we need to capture the cross-sequence triggering relations among events. To this end, BRUNCH allows us to identify the possible dependencies among multi-dimensional event sequences in hybrid MHPs. Specifically, it presents a class of prior distributions over branching structure according to intCRP, which has nested structure, inner intCRP and outer intCRP. Briefly, the inner intCRP identifies the possible triggering relations in each sequence independently, which are referred to as event links. Linked events in each sequence form one cluster. Subsequently, outer intCRP captures the potential cross-sequence triggering relations, referred to as cluster links, which connects parent events with children from cross-sequence clusters.
We resort to the Chinese Restaurant metaphor to describe the generative process of event links and cluster links in BRUNCH. Imagine a collection of event sequences as a collection of restaurants, and the events in each sequence as customers entering a restaurant. The linked events in each sequence compose one cluster, and such clusters correspond to tables. Figure 1(b) illustrates the process. Note that in traditional CRP, the probability of a customer sitting at a table is computed from the number of other customers already sitting at that table.
Event Link Construction
In each sequence, if one event is an immigrant, there exists one self-link with itself; otherwise, there exists a triggering dependency for the event. That is, if event  generates event
generates event 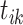 , the link from
, the link from  to
to 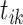 is created spontaneously. The inner intCRP assigns event link
is created spontaneously. The inner intCRP assigns event link 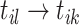 in a biased way, according to the following cluster-specific distribution:
in a biased way, according to the following cluster-specific distribution:
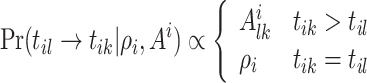 |
3.1 |
where self-affinity 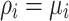 yields new immigrant events, and larger self-affinity favors more cascades.
yields new immigrant events, and larger self-affinity favors more cascades. 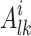 describes how the affinity between a pair of events affects the probability for
describes how the affinity between a pair of events affects the probability for  triggering
triggering 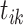 . In accordance with the propagation characteristics described by hybrid MHPs, child events tend to be generated by preceding events with stronger triggering effect. We define
. In accordance with the propagation characteristics described by hybrid MHPs, child events tend to be generated by preceding events with stronger triggering effect. We define 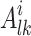 as the product of two parts:
as the product of two parts: 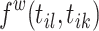 and
and 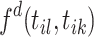 . For a window size W, we set the decay function
. For a window size W, we set the decay function 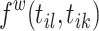 such that for
such that for 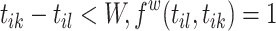 , and zero otherwise. It determines the probability to link with events that are at most W timespan away, and disregards the historical events as time progresses. Intuitively, the possible links existing between events that are far away from each other are negligibly rare. For
, and zero otherwise. It determines the probability to link with events that are at most W timespan away, and disregards the historical events as time progresses. Intuitively, the possible links existing between events that are far away from each other are negligibly rare. For 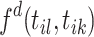 , we apply the self-triggering kernel
, we apply the self-triggering kernel 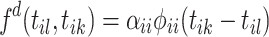 which decays the probability of connecting events along with the timespan to the current one. Consequently, the event links
which decays the probability of connecting events along with the timespan to the current one. Consequently, the event links 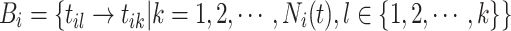 in i-th dimensional sequence assign events into clusters, where two events are assigned to the same cluster if one is reachable from the other by traversing the directed links. Once the event link
in i-th dimensional sequence assign events into clusters, where two events are assigned to the same cluster if one is reachable from the other by traversing the directed links. Once the event link 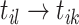 is confirmed, we can obtain the branching structure
is confirmed, we can obtain the branching structure  within sequences.
within sequences.
Cluster Link Construction
Accordingly, the collection of event links 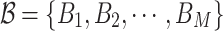 will divide the event sequences
will divide the event sequences 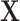 into clusters, denoted by
into clusters, denoted by 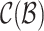 . By involving the mutual-triggering kernels, we could measure the pairwise affinity between cross-sequence events. Hence, given two clusters, s and g, the outer intCRP assigns the cluster link
. By involving the mutual-triggering kernels, we could measure the pairwise affinity between cross-sequence events. Hence, given two clusters, s and g, the outer intCRP assigns the cluster link 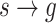 according to the following cascade-specific distribution:
according to the following cascade-specific distribution:
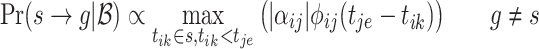 |
3.2 |
where 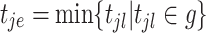 . Only if one event (i.e.,
. Only if one event (i.e.,
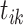 ) in cluster s generates the earliest event in cluster g, there exists a cluster link
) in cluster s generates the earliest event in cluster g, there exists a cluster link 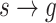 . In particular, self-loop cluster link is non-existent. Once the cluster link
. In particular, self-loop cluster link is non-existent. Once the cluster link 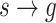 is determined, we could construct the equivalent branching structure
is determined, we could construct the equivalent branching structure  . In summary, we construct the complete branching structure
. In summary, we construct the complete branching structure 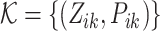 via scanning the obtained event links
via scanning the obtained event links 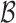 and cluster links
and cluster links 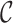 .
.
Intuitively, a collection of cluster links will divide clusters into cascades. We represent one cascade as one set of events. Let 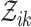 denote the cascade associated with event
denote the cascade associated with event 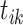 , and
, and 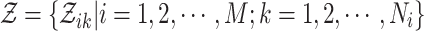 records the final cascade assignments. Notice that events
records the final cascade assignments. Notice that events 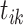 and
and 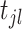 belong to one cascade (i.e.,
belong to one cascade (i.e.,
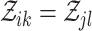 ) if and only if they are reachable via combinations of event links and cluster links. Given the collection of event links
) if and only if they are reachable via combinations of event links and cluster links. Given the collection of event links 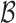 and cluster links
and cluster links 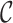 , we denote
, we denote 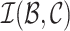 as the final collection of cascades. We initialize the Hawkes likelihood parameters
as the final collection of cascades. We initialize the Hawkes likelihood parameters 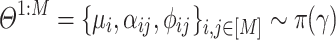 where
where 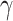 are the hyper-parameters, and
are the hyper-parameters, and 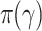 is the collection of distributions.
is the collection of distributions.
The central goal of BRUNCH is to infer the posterior distribution of the latent links 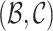 , given a collection of time-stamped events. It places a prior distribution over a combinatorial number of possible event links and cluster links, according to inner intCRP (Eq. 3.1) and outer intCRP (Eq. 3.2), respectively. Intuitively, applying Bayes’s Theorem, the posterior distribution takes the form
, given a collection of time-stamped events. It places a prior distribution over a combinatorial number of possible event links and cluster links, according to inner intCRP (Eq. 3.1) and outer intCRP (Eq. 3.2), respectively. Intuitively, applying Bayes’s Theorem, the posterior distribution takes the form 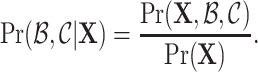 Unfortunately, we cannot compute
Unfortunately, we cannot compute  . Hence, the posterior inference of links is intractable. To address this, in the following section we present a strategy that approximately infers the posterior distribution.
. Hence, the posterior inference of links is intractable. To address this, in the following section we present a strategy that approximately infers the posterior distribution.
Model Inference
As the number of event links and cluster links varies with the observed events, we need to undertake Bayesian inference over a link set of unknown cardinality. Moreover, changes over event links may induce subsequent changes to other event links and current cluster links. To this end, we propose the Monte Carlo-based inference approach (MEDIA) that leverages the triggering nature of hybrid MHPs to sample event links and cluster links.
We aim to construct a Markov chain whose stationary distribution is the target posterior distribution 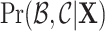 . The state of the chain is represented by
. The state of the chain is represented by  , a collection of links over event sequences. Furthermore, event links
, a collection of links over event sequences. Furthermore, event links 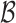 and cluster links
and cluster links 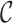 are strongly coupled, that is, sampling event links could trigger a chain of merges and splits to the current structure, as shown in Fig. 2. In view of this, we design the Monte Carlo-based inference approach, which involves two key phases: (a) sampling event links
are strongly coupled, that is, sampling event links could trigger a chain of merges and splits to the current structure, as shown in Fig. 2. In view of this, we design the Monte Carlo-based inference approach, which involves two key phases: (a) sampling event links 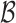 via a Metropolis-Hastings rule, which could possibly bring changes to current cluster links
via a Metropolis-Hastings rule, which could possibly bring changes to current cluster links 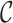 , and then (b) update cluster links
, and then (b) update cluster links 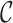 via a Gibbs sampler. We elaborate on them in turn.
via a Gibbs sampler. We elaborate on them in turn.
Fig. 2.
Sampling event links in Panel (a) leads a chain of changes to current branching structure, and constructs new one in Panel (b).
Sampling Event Links. Let current links be 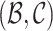 . After sampling one event link, the reconstructed links are denoted as
. After sampling one event link, the reconstructed links are denoted as 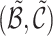 . The iterative procedure runs until approaching the stationary distribution as follows:
. The iterative procedure runs until approaching the stationary distribution as follows:
Using the current links
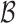 , sample a candidate link set
, sample a candidate link set 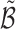 from the transition probability
from the transition probability 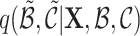 ;
;- Sampled
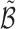 leads to cluster links
leads to cluster links 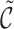 . Calculate the acceptance probability
. Calculate the acceptance probability 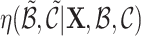 for the candidate set
for the candidate set  ,
,
Notice that we are considering the ratio of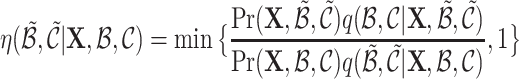
 under two different structures, so the denominator
under two different structures, so the denominator 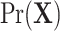 is eliminated.
is eliminated.
Theorem 4.1
The above Metropolis-Hastings rule satisfies detailed balance.
Based on Theorem 4.1, we can guarantee the resulting Markov chain converges to a stationary distribution uniquely [2]. BRUNCH provides a joint distribution for a collection of events and current links as following:
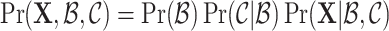 |
4.1 |
If one event is an offspring, it has only one parent event. So once the affinity functions in inner intCRP are predefined, the generated event links are conditionally independent. Furthermore, event links divide all events into clusters. Hence, once the event links and the affinity functions in outer intCRP are predefined, the generated cluster links are conditionally independent. That is to say, event links 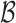 are conditionally independent given
are conditionally independent given 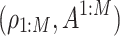 , and cluster links
, and cluster links 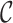 are conditionally independent given
are conditionally independent given 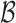 , thereby causing the independent cascades. As a consequence, the joint distribution on events and links equals to:
, thereby causing the independent cascades. As a consequence, the joint distribution on events and links equals to:
 |
4.2 |
The activities belonging to cascade I are represented as 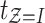 , hence,
, hence,
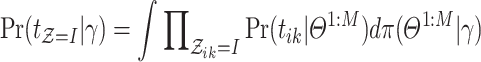 |
4.3 |
where the parameter set 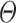 could be drawn from pre-determined distributions associated with the hyper-parameters
could be drawn from pre-determined distributions associated with the hyper-parameters 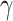 . Hence, the above integral is tractable. Based on the hybrid MHPs associated with conditional intensity (Eq. 2.1), we derive the conditional probability density [8] that an event occurs at time
. Hence, the above integral is tractable. Based on the hybrid MHPs associated with conditional intensity (Eq. 2.1), we derive the conditional probability density [8] that an event occurs at time 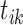 is:
is:
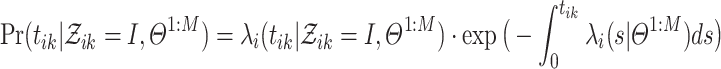 |
4.4 |
where the integral  is not always analytically integrable w.r.t. various link functions of hybrid MHPs. To address the issue, we propose the approximation:
is not always analytically integrable w.r.t. various link functions of hybrid MHPs. To address the issue, we propose the approximation: 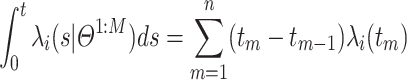 .
.
We describe how replacing an event link affects the current links  , and there are four cases:
, and there are four cases:
1. Split. If adding event link  breaks the existing link
breaks the existing link  and divides
and divides 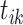 and
and  into two clusters, it shows that event
into two clusters, it shows that event 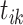 is an offspring. Moreover, there are no existing clusters to be merged after sampling event link
is an offspring. Moreover, there are no existing clusters to be merged after sampling event link 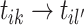 . Thus, the new cluster including
. Thus, the new cluster including  has the same incoming cluster links as the previous cluster containing both
has the same incoming cluster links as the previous cluster containing both 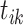 and
and  . We assume that the incoming links are independently linked to the new cluster with equal probability. New cluster s including
. We assume that the incoming links are independently linked to the new cluster with equal probability. New cluster s including 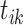 collects its outgoing cluster links
collects its outgoing cluster links  according to the distribution
according to the distribution 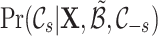 where
where 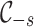 represents the set of cluster links excluding the ones
represents the set of cluster links excluding the ones 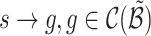 . Then, the transition probability is:
. Then, the transition probability is:
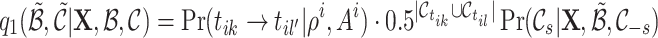 |
4.5 |
where 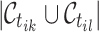 records the number of incoming cluster links for the old cluster containing both
records the number of incoming cluster links for the old cluster containing both 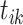 and
and  . Calculate
. Calculate 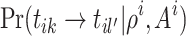 according to Eq. 3.1.
according to Eq. 3.1.
2. Split and Merge. Adding event link  breaks existing link
breaks existing link 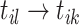 . Moreover, the cluster including event
. Moreover, the cluster including event  and the cluster including event
and the cluster including event  are merged after sampling event link
are merged after sampling event link 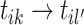 . Thus, the outgoing cluster links of new cluster retain the outgoing cluster links of the old cluster including
. Thus, the outgoing cluster links of new cluster retain the outgoing cluster links of the old cluster including 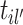 , and the incoming cluster links of new cluster combine the incoming cluster links connecting to the cluster including
, and the incoming cluster links of new cluster combine the incoming cluster links connecting to the cluster including 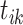 and the cluster including
and the cluster including 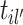 . The transition probability is:
. The transition probability is:
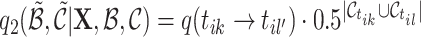 |
4.6 |
Also, the incoming cluster links are assumed to be assigned to the new merged cluster equally. When the sampling link 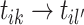 merges two clusters from one cascade,
merges two clusters from one cascade, 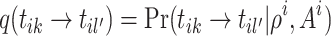 . Otherwise, when
. Otherwise, when 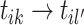 merges two clusters from different cascades, it combines the two cascades. Hence,
merges two clusters from different cascades, it combines the two cascades. Hence,
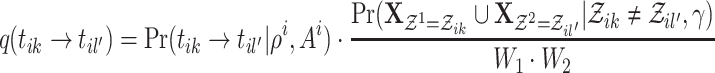 |
4.7 |
wherein 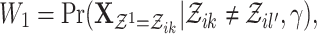 and
and 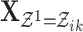 represents the events in the cascade
represents the events in the cascade 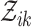 excluding the events in the cascade
excluding the events in the cascade 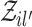 . Similarly,
. Similarly, 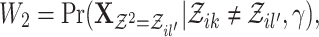 and
and 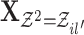 denotes the events in the cascade
denotes the events in the cascade 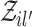 excluding the events in the cascade
excluding the events in the cascade 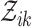 .
.
3. Merge. After adding event link 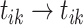 , if there is no new cluster to appear, it shows that event
, if there is no new cluster to appear, it shows that event 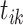 is an immigrant. Moreover, sampling event link
is an immigrant. Moreover, sampling event link 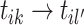 causes two existing clusters to be merged. Hence, the transition probability is:
causes two existing clusters to be merged. Hence, the transition probability is:
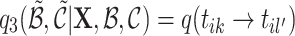 |
4.8 |
Considering the two merged clusters come from one cascade or two cascades,  is analogous to the analysis of
is analogous to the analysis of  .
.
4. No Change. There is no new cluster after setting 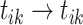 , and also no merge after sampling event link
, and also no merge after sampling event link 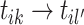 . In this case, the corresponding transition probability is:
. In this case, the corresponding transition probability is: 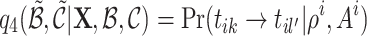 .
.
Obviously, after sampling each event link, the resulting split (i.e., case 1) and merge (i.e., case 3) are inverse of each other, meanwhile, the other two cases (i.e., split and merge vs. no change) are inverse transform. Accordingly, by taking the inverse pairs, we derive the corresponding acceptance ratios 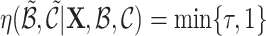 , where the Hastings ratio
, where the Hastings ratio 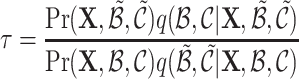 .
.
As aforementioned, sampling an event link may lead four possible changes to current links  . Hence, the corresponding Hastings ratio is:
. Hence, the corresponding Hastings ratio is:
- A single offspring event becomes an immigrant and the previous cluster is split into two clusters. Thus the candidate partition structure
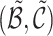 is generated. The transitions corresponding to
is generated. The transitions corresponding to 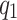 and
and 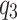 are the inverse of each other. Substituting Eq. 4.1, 4.5 and 4.8, the Hastings ratio works out to be
are the inverse of each other. Substituting Eq. 4.1, 4.5 and 4.8, the Hastings ratio works out to be
When the offspring event changes its parent event from one cluster to another cluster under the condition that the two clusters locate in different cascades, the reverse transition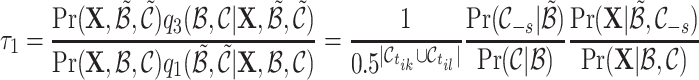
4.9  leads to the merger of two cascades. Consequently, the transition probability is:
leads to the merger of two cascades. Consequently, the transition probability is:
Similarly,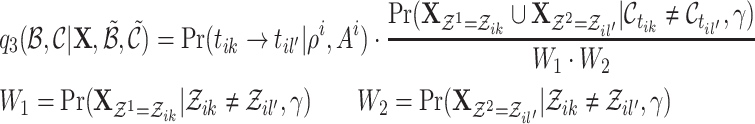
. The corresponding transition probability becomes:
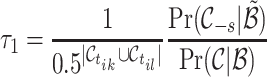
- A single offspring event switches to an immigrant, and sampling a new event link leads to the combination of two local clusters. In this case, the transitions corresponding to
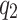 and
and 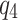 are the inverse of each other. If the two merged clusters come from one cascade,
are the inverse of each other. If the two merged clusters come from one cascade,
If the sampling new event link causes two cascades to be merged, we obtain
4.10  .
. Sampling
 leads the immigrant event
leads the immigrant event 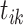 to trigger new offspring. Similar to
to trigger new offspring. Similar to 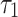 , we can calculate the Hastings ratios:
, we can calculate the Hastings ratios: 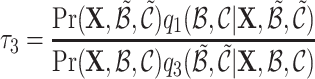 .
.Samplings which change event links but cause no change to the cluster links always have
 .
.
Sampling Cluster Links. Once the event links 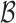 are sampled via the aforementioned Metropolis-Hasting rule, we update the cluster links
are sampled via the aforementioned Metropolis-Hasting rule, we update the cluster links  again via Gibbs sampler as follows: [i)] Scan each cluster
again via Gibbs sampler as follows: [i)] Scan each cluster 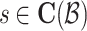 ; [ii)] Draw
; [ii)] Draw  Repeat the above steps until convergence.
Repeat the above steps until convergence.  represents the outgoing cluster links for cluster s, and
represents the outgoing cluster links for cluster s, and  records the set of cluster links excluding the ones
records the set of cluster links excluding the ones  . We calculate
. We calculate 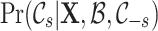 according to Eq. 3.2.
according to Eq. 3.2.
We keep all event links in an adjacency matrix 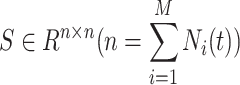 , wherein rows and columns are indexed by ordered events from all sequences, value 1 or 0 is recorded in entry
, wherein rows and columns are indexed by ordered events from all sequences, value 1 or 0 is recorded in entry 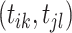 according to whether
according to whether 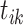 triggers
triggers 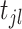 or not. The formal description of MEDIA, is given in [9]. The time complexity of MEDIA is
or not. The formal description of MEDIA, is given in [9]. The time complexity of MEDIA is 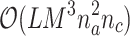 [9].
[9].
Experiments
In this section, we investigate the performance of our model and inference algorithm and report the key results. All experiments are performed on a machine with 16 GB RAM with Intel(R) Core(TM) E5-1620V2 CPU@3.70 GHz processor running on Windows 8.1 Pro.
Competitors. Recall that there is no existing work that infers the branching structure of nonlinear MHPs. Hence, we are confined to compare our proposed frameworks to techniques that infer the branching structure of linear MHPs in [12, 17]. In particular, we consider the following strategies for our study. (a) Cluster-L: Based on the alternative representation of the linear Hawkes process in terms of cluster Poisson processes, [12, 17] propose the cluster-based method. (b) MEDIA-L: Use MEDIA to infer the branching structure of linear MHPs. (c) MEDIA-E: Apply MEDIA to infer the branching structure of exponential MHPs (i.e., the corresponding link function 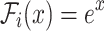 ). (d) MEDIA-H: The odd dimensions of MHPs take linear link function, and the even dimensions adopt exponential one. Then we use MEDIA to infer the branching structure of hybrid MHPs.
). (d) MEDIA-H: The odd dimensions of MHPs take linear link function, and the even dimensions adopt exponential one. Then we use MEDIA to infer the branching structure of hybrid MHPs.
As mentioned earlier, BRUNCH is not sensitive to shapes of the triggering kernel functions in hybrid MHPs. Hence, we adopt an exponential kernel function 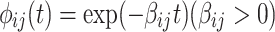 in the experiments (see [9] for the performance associated with other kernel functions). For each dimension, the hyper-parameter
in the experiments (see [9] for the performance associated with other kernel functions). For each dimension, the hyper-parameter  is sampled by a uniform distribution
is sampled by a uniform distribution 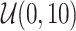 . The base intensity
. The base intensity 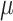 is set varying over dimensions and is sampled from
is set varying over dimensions and is sampled from 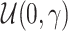 , then the coefficient
, then the coefficient  is sampled from
is sampled from  , and the decay parameter
, and the decay parameter 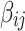 has the form of
has the form of 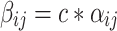 where c is sampled from
where c is sampled from 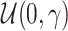 . The initial parameters
. The initial parameters 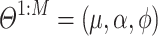 need satisfy the stability and uniqueness conditions (see details in [9]). Additionally, we set the time window size to
need satisfy the stability and uniqueness conditions (see details in [9]). Additionally, we set the time window size to 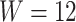 h.
h.
Datasets and Ground Truth. We fit the aforementioned models on two real-world social media datasets: (1) Facebook (Fa): 43, 679, 231 events from 109, 211 individuals during March 2018 to May 2018; (2) Twitter (Tw): 51, 622, 139 events from 123, 972 individuals from March 2018 to May 2018. While crawling the triggering relations of events (i.e., which event triggers which events) as ground truth via Facebook Graph API and Twitter Streaming API, we crawl the social network structure in advance. For each immigrant event in each individual’s sequence, we grab the triggered events (i.e., offsprings) starting from the individual’s followers via a depth-first search algorithm. Then, while modeling the observed timestamped events via MHPs, we aim to infer the branching structure without the knowledge of social network structure.
Inferring Branching Structure. We convert the branching structure to a binary matrix S as mentioned in Sect. 4. Given the estimated links 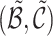 , we update
, we update  according to
according to  , and then derive the across-dimensional branching structure
, and then derive the across-dimensional branching structure  from
from 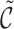 before filling in the final
before filling in the final 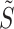 . Afterwards, comparing the estimated matrix
. Afterwards, comparing the estimated matrix 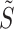 with the ground truth S, we evaluate the effectiveness for all the aforementioned strategies in terms of F1-Score.
with the ground truth S, we evaluate the effectiveness for all the aforementioned strategies in terms of F1-Score.
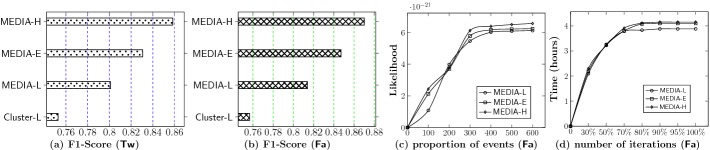
Figures 3(a) and 3(b) plot the results. Clearly, our proposed model BRUNCH with MEDIA outperforms the baseline Cluster-L, obtaining higher inference F1-Score. That is, the triggering relations among events (i.e., branching structure of MHPs) identified by the MEDIA approach are more reliable. While applying the same inferring procedure MEDIA, hybrid MHPs (mixing exponential MHPs and linear MHPs) show superior inference performance compared to other alternatives. In particular, MEDIA-H is superior to MEDIA-L and MEDIA-E. This further verifies the justifiability of our proposed hybrid MHPs.
Fig. 3.
Experimental results.
Convergence. We compare the convergence rate of our proposed techniques in Fig. 3(c) on Facebook data. The results on Twitter are qualitatively similar (see [9]). Clearly, MEDIA-H is of higher likelihood than MEDIA-L and MEDIA-E. This further validates the usefulness of our hybrid MHPs.
Scalability. Figures 3(d) plots the scalability of our algorithms with increasing events on Facebook data. The results are qualitatively similar on Twitter (see [9]). We run the inference methods on different sizes of datasets (i.e., slice different percentages of events in datasets as input data for BRUNCH). Observe that the average inference time of MEDIA stabilizes with increasing number of events. Since the number of event links and cluster links grows significantly as events increases, we expect the average runtime of MEDIA becomes relatively stable when more than 70% input data are utilized.
Conclusions
In this paper, we propose a novel probabilistic model called BRUNCH to infer the branching structure of hybrid MHPs. It bridges a significant chasm between hybrid MHPs (nonlinear MHPs as well) and branching structure inference. We handle the inferencing procedure via the MEDIA method, which provides a heuristic to make coordinated changes to both event links within clusters and cluster links within cascades. Empirically, our model demonstrates good performance and application potential in the real world.
Acknowledgments
This work is partly supported by the National Natural Science Foundation of China (No. 61672408, 61972309) and National Engineering Laboratory of China for Public Safety Risk Perception and Control by Big Data (PSRPC).
Footnotes
Link functions describe the dynamics of the comprehensive effects from previous events.
Triggering kernel functions describe the dynamics of how previous events trigger future events and may vary widely across different applications, e.g., the triggering patterns in social media can be very different from the ones in high frequency trading.
Contributor Information
Hady W. Lauw, Email: hadywlauw@smu.edu.sg
Raymond Chi-Wing Wong, Email: raywong@cse.ust.hk.
Alexandros Ntoulas, Email: antoulas@di.uoa.gr.
Ee-Peng Lim, Email: eplim@smu.edu.sg.
See-Kiong Ng, Email: seekiong@nus.edu.sg.
Sinno Jialin Pan, Email: sinnopan@ntu.edu.sg.
Hui Li, Email: HLI019@e.ntu.edu.sg.
Hui Li, Email: hli@xidian.edu.cn.
Sourav S. Bhowmick, Email: assourav@ntu.edu.sg
References
- 1.Bacry E, Muzy JF. Hawkes model for price and trades high-frequency dynamics. Quant. Finance. 2014;14:1147–1166. doi: 10.1080/14697688.2014.897000. [DOI] [Google Scholar]
- 2.Bishop CM. Pattern Recognition and Machine Learning. Heidelberg: Springer; 2006. [Google Scholar]
- 3.Blei DM, Frazier PI. Distance dependent Chinese restaurant processes. JMLR. 2011;12:2461–2488. [Google Scholar]
- 4.Farajtabar, M., Du, N., Rodriguez, M.G., Valera, I., Zha, H., Song, L.: Shaping social activity by incentivizing users. In: NIPS (2014) [PMC free article] [PubMed]
- 5.Hawkes AG. Point spectra of some mutually exciting point processes. J. Roy. Stat. Soc.: Ser. B (Methodol.) 1971;33:438–443. [Google Scholar]
- 6.Hawkes AG. Spectra of some self-exciting and mutually exciting point processes. Biometrika. 1971;58:83–90. doi: 10.1093/biomet/58.1.83. [DOI] [Google Scholar]
- 7.Hawkes AG, Oakes D. A cluster process representation of a self-exciting process. J. Appl. Probab. 1974;11:493–503. doi: 10.2307/3212693. [DOI] [Google Scholar]
- 8.Lee, Y., Lim, K.W., Ong, C.S.: Hawkes processes with stochastic excitations. In: ICML (2016)
- 9.Li, H., Li, H., Bhowmick, S.S.: Brunch: branching structure inference of hybrid multivariate Hawkes processes with application to social media. Technical report http://www.ntu.edu.sg/home/assourav/TechReports/BRUNCH-TR.pdf
- 10.Mei, H., Eisner, J.M.: The neural Hawkes process: A neurally self-modulating multivariate point process. In: NIPS (2017)
- 11.Møller J, Rasmussen JG. Perfect simulation of Hawkes processes. Adv. Appl. Probab. 2005;37:629–646. doi: 10.1239/aap/1127483739. [DOI] [Google Scholar]
- 12.Rasmussen JG. Bayesian inference for Hawkes processes. Methodol. Comput. Appl. Probab. 2013;15:623–642. doi: 10.1007/s11009-011-9272-5. [DOI] [Google Scholar]
- 13.Reynaud-Bouret P, Rivoirard V, Grammont F, Tuleau-Malot C. Goodness-of-fit tests and nonparametric adaptive estimation for spike train analysis. J. Math. Neurosci. (JMN) 2014;4(1):1–41. doi: 10.1186/2190-8567-4-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Wang, Y., Theodorou, E., Verma, A., Song, L.: A stochastic differential equation framework for guiding online user activities in closed loop. In: AISTATS (2018)
- 15.Zhang C. Modeling high frequency data using hawkes processes with power-law kernels. Procedia Comput. Sci. 2016;80:762–771. doi: 10.1016/j.procs.2016.05.366. [DOI] [Google Scholar]
- 16.Zhou, K., Zha, H., Song, L.: Learning social infectivity in sparse low-rank networks using multi-dimensional Hawkes processes. In: AISTATS (2013)
- 17.Zhou, K., Zha, H., Song, L.: Learning triggering kernels for multi-dimensional Hawkes processes. In: ICML (2013)