Computational DFT data related to the redox behaviour of tris(β-diketonato)ruthenium(III) compounds

Abstract

The data presented in this paper are related to the research article titled “Redox Behaviour of [Ru(β-diketonato)₃] Compounds” [1]. This paper presents structural and energy data obtained from the density functional theory (DFT) computations. The energy data is related to experimentally obtained redox potential values. Various relationships are presented for the Ru^III/II and Ru^III/IV redox couples, involving both their experimental redox data as well as DFT calculated data, such as frontier orbital energies (E_HOMO and E_LUMO) and calculated Mulliken electronegativity values.

Specifications Table

Subject	Chemistry
Specific subject area	Computational chemistry
Type of data	Table Graph Figure
How data were acquired	Electronic structure calculations, using the Amsterdam Density Functional (ADF) 2018 and Gaussian 16 programmes.
Data format	Raw Analyzed
Parameters for data collection	Input coordinates were constructed manually, using ChemCraft
Description of data collection	Computational DFT data was obtained with the ADF 2018 and Gaussian 16 programmes on the High Performance Computing facility of the University of the Free State
Data source location	Department of Chemistry, University of the Free State, Nelson Mandela Street, Bloemfontein, South Africa
Data accessibility	Data is included with article and in the supplementary file
Related research article	J. Conradie, Redox Behaviour of [Ru(β-diketonato)3] Compounds. Electrochim. Acta. 337 (2020) 135801. https://doi:10.1016/j.electacta.2020.135801.

Value of the Data

• •Density functional theory (DFT) calculated optimized xyz-data (coordinates) for a series of 14 tris(β-diketonato)ruthenium(III) compounds are provided
• •DFT optimized geometrical data (coordinates) can be used to visualize the DFT calculated structures of a series of 14 tris(β-diketonato)ruthenium(III) compounds
• •This data provides highest occupied molecular orbital (HOMO) and lowest unoccupied molecular orbital (LUMO) energies (E_HOMO and E_LUMO) of different tris(β-diketonato)ruthenium(III) compounds
• •Relationships between experimental redox data and DFT calculated frontier orbital energies and calculated Mulliken electronegativity (χ) for tris(β-diketonato)ruthenium(III) compounds containing different electron donating and electron withdrawing substituents, obtained by different DFT methods, all produced similar R² values
• •E_HOMO, E_LUMO and χ_calc data obtained by the different DFT methods show the same trend, namely [Ru(β-diketonato)₃] compounds containing electron withdrawing substituents on the β-diketonato ligand have lower E_HOMO and E_LUMO, and higher χ_calc values than [Ru(β-diketonato)₃] compounds containing electron donating substituents on the β-diketonato ligand
• •Electronic energy data of different spin states of neutral, oxidized and reduced tris(acetylacetonato)ruthenium(III) provide the lowest energy spin state of the neutral, oxidized and reduced tris(acetylacetonato)ruthenium(III)
• •Linear relationships obtained from this data enable further prediction of the properties of novel complexes prior to synthesis, to be confirmed by laboratory tests

1. Data Description

This data article provides data related to Ru(III) compounds 1 – 14 (Fig. 1). A summary of the Hammett meta-substituent sigma constants, σ_R [2], of both the R and Rꞌ substituents on the β-diketonato ligand of the [Ru(β-diketonato)₃] compounds 1 – 14, is provided in Table 1. The σ_R values provide an indication of the electron donating (smaller value) and electron withdrawing (larger value) property of the individual substituents R and Rꞌ on the β-diketonato ligand of the [Ru(β-diketonato)₃] compounds 1 – 14. On the other hand, the data of the sum (σ_R + σ_R') provides an indication of the electron donating (smaller value) and electron withdrawing (larger value) property of the β-diketonato ligand with its two substituents.

Fig. 1.

Structure of the fourteen [Ru(β-diketonato)₃] compounds 1 – 14.

Table 1.

Hammett meta-substituent sigma constants, σ_R, of the individual R and Rꞌ groups [2] substituted on the β-diketonato ligand of the [Ru(β-diketonato)₃] compounds 1 – 14, with the R and Rꞌ substituents as shown in Fig. 1. (σ_R+ σ_Rꞌ) gives the combined electronic effect of each ligand containing two substituents.

Compound no	R	R'	σR	σR'	(σR + σR')
1	CF3	CF3	0.43	0.43	0.86
2	CF3	C4H3O	0.43	0.06	0.49
3	CF3	C4H3S	0.43	0.09	0.52
4	CF3	Ph	0.43	0.06	0.49
5	CF3	CH3	0.43	-0.069	0.36
6	CF3	C(CH3)3	0.43	-0.1	0.33
7	Ph	Ph	0.06	0.06	0.12
8	CH3	Ph	-0.069	0.06	-0.01
9	CH3	CH3	-0.069	-0.069	-0.14
10	C(CH3)3	C(CH3)3	-0.10	-0.10	-0.20
11	Et	Et	-0.07	-0.07	-0.14
12	Pr	Pr	-0.06	-0.06	-0.12
13	Bu	Bu	-0.08	-0.08	-0.16
14	iPr	iPr	-0.04	-0.04	-0.08

Ru(III) compounds 1 – 14 (Fig. 1) were optimized by different density functional theory (DFT) methods in the solvent phase (CH₃CN). Table 2 and Table 3 lists the DFT solvent phase (CH₃CN) computed data, namely the highest occupied molecular orbital (HOMO) and lowest unoccupied molecular orbital (LUMO) energies (E_HOMO and E_LUMO) and Mulliken electronegativity (χ_calc, a measure of the tendency of an atom or molecule to attract electrons [3]) of the series of tris(β-diketonato)ruthenium(III) compounds 1 – 14 (Fig. 1). Experimental electrochemical data (potential E vs Fc/Fc⁺) of compounds 1 – 14, obtained from literature [4,5], are also given in Table 2. Different E_HOMO, E_LUMO and χ_calc values are obtained by the different DFT methods, though all methods show the same trend, namely [Ru(β-diketonato)₃] compounds containing electron withdrawing substituents on the β-diketonato ligand (e.g. complexes 1 – 6 containing a CF₃ group) have lower E_HOMO and E_LUMO, and higher χ_calc values than [Ru(β-diketonato)₃] compounds containing electron donating substituents on the β-diketonato ligand (e.g. complexes 9 – 14), see Table 2 and Table 3.

Table 2.

DFT calculated data from this data article, as well as experimental electrochemical data (E vs Fc/Fc⁺) obtained from literature [4,5], of the [Ru(β-diketonato)₃] compounds 1 – 14. Where β-diketonato ligand = (RCOCHCORꞌ)^— with the R and Rꞌ substituents as shown in Fig. 1. DFT data was computed using two different gga functionals PW91 and OLYP.

	R	R'	E (RuIII/II)a	E (RuIII/IV)a	PW91/STO-TZ2P			OLYP/STO-TZ2P
					EHOMO (eV)	ELUMO (eV)	χcalc (eV)c	EHOMO (eV)	ELUMO (eV)	χcalc (eV)b
1	CF3	CF3	0.34		-5.856	-5.585	5.720	-5.573	-5.337	5.455
2	CF3	C4H3O	-0.34	1.20	-5.067	-4.744	4.906	-4.793	-4.522	4.657
3	CF3	C4H3S	-0.35	1.19	-5.014	-4.753	4.883	-4.766	-4.486	4.626
4	CF3	Ph	-0.35	1.26	-5.134	-4.838	4.986	-4.865	-4.606	4.736
5	CF3	CH3	-0.47	1.29	-5.132	-4.812	4.972	-4.869	-4.596	4.733
6	CF3	C(CH3)3	-0.55	1.30	-5.065	-4.777	4.921	-4.782	-4.513	4.648
7	Ph	Ph	-0.90	0.66	-4.622	-4.294	4.458	-4.339	-4.070	4.205
8	CH3	Ph	-1.04	0.64	-4.529	-4.193	4.361	-4.260	-3.969	4.114
9	CH3	CH3	-1.16	0.61	-4.437	-4.137	4.287	-4.176	-3.911	4.044
10	C(CH3)3	C(CH3)3	-1.46	0.44	-4.125	-3.843	3.984	-3.823	-3.581	3.702
11	Et	Et	-1.308	0.549	-4.335	-4.004	4.170	-4.056	-3.785	3.921
12	Pr	Pr	-1.324	0.547	-4.316	-4.001	4.158	-4.039	-3.768	3.903
13	Bu	Bu	-1.330	0.535	-4.307	-3.979	4.143	-4.024	-3.766	3.895
14	iPr	iPr	-1.392	0.509	-4.196	-3.930	4.063	-3.900	-3.682	3.791

^aExperimental values for E vs Fc/Fc⁺ from references [4,5]. In order to convert to potential vs Fc/Fc⁺ for comparative reasons, the following values have been used:

E°' (Fc/Fc⁺) = 0.66(5) V vs NHE in solvent [ⁿ(Bu₄)N][PF₆]/CH₃CN [9]; Saturated calomel (SCE) = 0.2444 V vs NHE; Ag/Ag⁺ = 0.400 V vs SCE [10].

^bχ = Electronegativity

Table 3.

DFT calculated data from this data article, as well as experimental electrochemical data (E vs Fc/Fc⁺) obtained from literature [4,5], of the [Ru(β-diketonato)₃] compounds 1 – 14. Where β-diketonato ligand = (RCOCHCORꞌ)^— with the R and Rꞌ substituents as shown in Fig. 1. DFT data was computed using two different hybrid functionals OPBE0 and B3LYP.

	R	R'	E (RuIII/II) a	E (RuIII/IV) a	OPBE0/STO-TZ2P			B3LYP/STO-TZ2P			B3LYP/STO-6-311G(d,p)/Lanl2dz
					EHOMO (eV)	ELUMO (eV)	χcalc (eV) c	EHOMO (eV)	ELUMO (eV)	χcalc (eV) c	EHOMO (eV)	ELUMO (eV)	χcalc (eV) c
1	CF3	CF3	0.34		-7.183	-4.200	5.692	-6.938	-4.558	5.748	-7.507	-3.272	5.389
2	CF3	C4H3O	-0.34	1.20	-6.404	-3.408	4.906	-6.103	-3.725	4.914	-6.607	-2.768	4.688
3	CF3	C4H3S	-0.35	1.19	-6.393	-3.410	4.901	-6.074	-3.707	4.890	-6.635	-2.822	4.729
4	CF3	Ph	-0.35	1.26	-6.528	-3.482	5.005	-6.168	-3.765	4.967	-6.777	-2.758	4.767
5	CF3	CH3	-0.47	1.29	-6.519	-3.413	4.966	-6.211	-3.792	5.001	-6.815	-2.414	4.615
6	CF3	C(CH3)3	-0.55	1.30	-6.420	-3.341	4.881	-6.165	-3.732	4.949	-6.745	-2.353	4.549
7	Ph	Ph	-0.90	0.66	-5.987	-2.978	4.483	-5.620	-3.211	4.415	-6.229	-2.405	4.317
8	CH3	Ph	-1.04	0.64	-5.922	-2.863	4.393	-5.595	-3.132	4.364	-6.216	-2.137	4.177
9	CH3	CH3	-1.16	0.61	-5.863	-2.719	4.291	-5.215	-2.785	4.000	-6.166	-1.634	3.900
10	C(CH3)3	C(CH3)3	-1.46	0.44	-5.467	-2.403	3.935	-5.215	-2.785	4.000	-6.021	-1.474	3.748
11	Et	Et	-1.308	0.549	-5.722	-2.588	4.155	-5.435	-2.962	4.199	-6.151	-1.648	3.900
12	Pr	Pr	-1.324	0.547	-5.703	-2.577	4.140	-5.415	-2.938	4.177	-6.136	-1.633	3.884
13	Bu	Bu	-1.330	0.535	-5.681	-2.565	4.123	-5.415	-2.946	4.180	-6.130	-1.619	3.874
14	iPr	iPr	-1.392	0.509	-5.523	-2.470	3.996	-5.289	-2.836	4.062	-6.123	-1.591	3.857

^aExperimental values for E vs Fc/Fc⁺ from references [4,5]. In order to convert to potential vs Fc/Fc⁺ for comparative reasons, the following values have been used:

E°' (Fc/Fc⁺) = 0.66(5) V vs NHE in solvent [ⁿ(Bu₄)N][PF₆]/CH₃CN [9]; Saturated calomel (SCE) = 0.2444 V vs NHE; Ag/Ag⁺ = 0.400 V vs SCE [10].

^bχ = Electronegativity

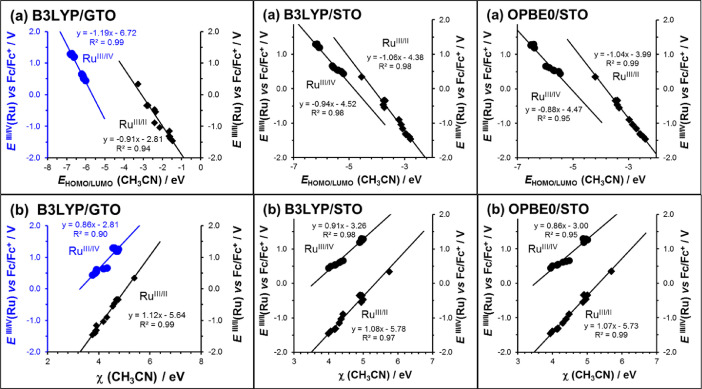
The relationships between the experimental values of the reduction (Ru^III/II) and oxidation (Ru^III/IV) couples [4,5] and the solvent (CH₃CN) phase calculated E_HOMO and E_LUMO energies and their χ_calc and ω_calc values, obtained via different DFT methods using generalized gradient approximations (gga) functionals, PW91/TZ2P and OLYP/TZ2P, are shown in Fig. 2 and obtained via different DFT methods using hybrid functionals, B3LYP/6-311G(d,p)/Lanl2dz, B3LYP/TZ2P and OPBE0/TZ2P, are shown in Fig. 3. The relationships obtained by these different solvent phase DFT methods, taking the experimental solvent (CH₃CN) used for electrochemical experiments [4,5] into account in the calculations, all produced similar R² values, comparable with the gas phase B3LYP/6-311G(d,p)/Lanl2dz calculated relationships obtained from reference [1]. The slopes of the experimental Ru^III/II and Ru^III/IV redox values versus the solvent (CH₃CN) phase calculated E_HOMO and E_LUMO energies, are steeper than the corresponding gas phase calculated slope and also closer to nearing a gradient of -1.

Fig. 2.

Relationships obtained between the experimental redox potential E°' (vs Fc/Fc⁺) of both the reduction (Ru^III/II) and the oxidation (Ru^III/IV) redox couples of the fourteen [Ru(β-diketonato)₃] compounds 1 – 14 of this data article, with the DFT calculated data, namely (a) the LUMO (Ru^III/II) and HOMO (Ru^III/IV) energies E_HOMO/LUMO, (b) calculated Mulliken electronegativity χ. All calculations were conducted in CH₃CN as solvent, using the indicated gga functionals.

Fig. 3.

Relationships obtained between the experimental redox potential E°' (vs Fc/Fc⁺) of both the reduction (Ru^III/II) and the oxidation (Ru^III/IV) redox couples of the fourteen [Ru(β-diketonato)₃] compounds 1 – 14 of this data article, with the DFT calculated data, namely (a) the LUMO (Ru^III/II) and HOMO (Ru^III/IV) energies E_HOMO/LUMO and (b) calculated Mulliken electronegativity χ. All calculations were conducted in CH₃CN as solvent, using the indicated hybrid functionals.

Redox potentials and frontier orbital energies

Oxidation redox couple Ru^III/IV:

E°'(RuIII/IV) = -0.80 EHOMO(RuIII) – 4.00	R2 = 0.98	(gas phase B3LYP/6-311G(d,p)/Lanl2dz) [1]
E°'(RuIII/IV) = -1.19 EHOMO(RuIII) – 6.72	R2 = 0.99	(CH3CN phase B3LYP/6-311G(d,p)/Lanl2dz)
E°'(RuIII/IV) = -0.94 EHOMO(RuIII) – 4.52	R2 = 0.98	(CH3CN phase B3LYP/TZ2P)
E°'(RuIII/IV) = -0.88 EHOMO(RuIII) – 4.47	R2 = 0.95	(CH3CN phase OPBE0/TZ2P)
E°'(RuIII/IV) = -0.90 EHOMO(RuIII) – 3.33	R2 = 0.96	(CH3CN phase PW91/TZ2P)
E°'(RuIII/IV) = -0.87 EHOMO(RuIII) – 2.98	R2 = 0.96	(CH3CN phase OLYP/TZ2P)

Reduction redox couple Ru^III/II:

E°'(RuIII/II) = -0.72 ELUMO(RuIII) – 2.21	R2 = 0.98	(gas phase B3LYP/6-311G(d,p)/Lanl2dz) [1]
E°'(RuIII/II) = -0.91 ELUMO(RuIII) – 2.81	R2 = 0.94	(CH3CN phase B3LYP/6-311G(d,p)/Lanl2dz)
E°'(RuIII/II) = -1.06 ELUMO(RuIII) – 4.38	R2 = 0.98	(CH3CN phase B3LYP/TZ2P)
E°'(RuIII/II) = -1.04 ELUMO(RuIII) – 3.99	R2 = 0.99	(CH3CN phase OPBE0/TZ2P)
E°'(RuIII/II) = -1.08 ELUMO(RuIII) – 5.59	R2 = 0.98	(CH3CN phase PW91/TZ2P)
E°'(RuIII/II) = -1.08 ELUMO(RuIII) – 5.36	R2 = 0.98	(CH3CN phase OLYP/TZ2P)

HOMO (LUMO) energies are directly related to the absolute oxidation potential since the product of the HOMO (LUMO) energies (in eV) and the electron charge (-1) gives absolute oxidation potential in eV [6]. The nearer the slope of the graph of oxidation (reduction) potential versus HOMO (LUMO) energies is to -1, the more accurate the DFT method used to calculate the HOMO (LUMO) energies. The intercept of the graph should be equal to the absolute potential of reference used, namely the Fc⁺/Fc couple in acetonitrile for which benchmark values varies between +4.97 V (SMDB3LYP-D2/def2-QZVPPD//B3LYP/LanL2TZf/6-31G(d)) [7] and 4.988 V (G3(MP2)-RAD-Full-TZ using gas-phase energies and COSMO-RS solvation energies) [8]. In this study slopes of 0.7 – 1.2 and intercepts of 2.21 – 6.71 are obtained.

Redox potentials and global Mulliken electronegativity:

Oxidation redox couple Ru^III/IV:

E°'(RuIII/IV) = 0.67 χcalc – 1.80	R2 = 0.96	(gas phase B3LYP/6-311G(d,p)/Lanl2dz) [1]
E°'(RuIII/IV) = 0.86 χcalc – 2.81	R2 = 0.90	(CH3CN phase B3LYP/6-311G(d,p)/Lanl2dz)
E°'(RuIII/IV) = 0.91 χcalc – 3.26	R2 = 0.98	(CH3CN phase B3LYP/TZ2P)
E°'(RuIII/IV) = 0.86 χcalc – 3.00	R2 = 0.95	(CH3CN phase OPBE0/TZ2P)
E°'(RuIII/IV) = 0.90 χcalc – 3.19	R2 = 0.97	(CH3CN phase PW91/TZ2P)
E°'(RuIII/IV) = 0.89 χcalc – 2.91	R2 = 0.96	(CH3CN phase OLYP/TZ2P)

Reduction redox couple Ru^III/II:

E°'(RuIII/II) = 0.81 χcalc – 4.09	R2 = 0.98	(gas phase B3LYP/6-311G(d,p)/Lanl2dz) [1]
E°'(RuIII/II) = 1.12 χcalc – 5.64	R2 = 0.99	(CH3CN phase B3LYP/6-311G(d,p)/Lanl2dz)
E°'(RuIII/II) = 1.08 χcalc – 5.78	R2 = 0.97	(CH3CN phase B3LYP/TZ2P)
E°'(RuIII/II) = 1.07 χcalc – 5.93	R2 = 0.99	(CH3CN phase OPBE0/TZ2P)
E°'(RuIII/II) = 1.09 χcalc – 5.79	R2 = 0.98	(CH3CN phase PW91/TZ2P)
E°'(RuIII/II) = 1.08 χcalc – 5.51	R2 = 0.98	(CH3CN phase OLYP/TZ2P)

The energies relative to the ground state energy for the different possible spin states of the neutral, oxidized and reduced [Ru(acetylacetonato)₃] compound 9 are provided in Table 4. The lowest energy value for each spin state showed that the neutral compound is low spin, S = ½ (doublet, one unpaired electron), in agreement with experiment [11]. The anion is diamagnetic with S = 0 (singlet), and the cation is paramagnetic with S = 1 (triplet, two unpaired electrons).

Table 4.

DFT calculated relative energy (eV) data obtained from this data article, for the different possible spin states of the neutral, oxidized and reduced [Ru(acetylacetonato)₃], complex 9. The lowest energy value for each of the neutral, oxidized and reduced states, is taken as 0.

	Spin	B3LYP	PW91
anion	0	0.00	0.00
	1	1.27	1.51
	2	-	2.41
neutral	1/2	0.00	0.00
	3/2	1.42	1.61
	5/3	2.15	3.84
cation	0	0.40	0.27
	1	0.00	0.00
	2	0.00	1.79

2. Experimental Design, Materials, and Methods

DFT calculations on all fourteen [Ru(β-diketonato)₃] compounds were performed in the CH₃CN solvent phase, using the following DFT methods:

• (i)B3LYP/GTO-6-311G(d,p)/Lanl2dz: The hybrid functional B3LYP, which is composed of the Becke 88 exchange functional was applied in combination with the LYP correlation functional, as implemented in the Gaussian 16 package [12], applying the GTO (Gaussian type orbital) triple-ζ basis set 6-311G(d,p) for the lighter atoms (C, H, N, O, F) and the Lanl2dz (Los Alamos National Laboratory 2-double-ζ) basis set for the heavier Ru metal. The optimization is performed using Berny algorithm using GEDIIS [13] as implemented in the Gaussian 16 suite of programs [12]. The convergence is reached when the root mean square force, the maximum force, the root mean square displacement and the maximum displacement are within the threshold of 0.00030, 0.00045, 0.0012 and 0.0018 atomic units, respectively. The requested convergence on energy is 1.0D-6 atomic unit. The solvation model density (SMD) of the polarizable continuum model (PCM) was used, which also solved the non-homogeneous Poisson equation, by applying the integral equation formalism variant (IEF-PCM), as implemented in the Gaussian 16 package [12].
• (ii)PW91/STO-TZ2P: Scalar-relativistic DFT using the gga PW91 (Perdew-Wang 1991) functional with the all-electron STO (Slater-Type Orbitals) triple ζ basis set with two polarization functions (TZ2P) was applied, as implemented in the ADF 2018 package [14]. The geometry optimizations procedure in ADF is based on a quasi Newton approach, with an approximate Hessian. The Hessian is updated in the process of optimization. By default delocalized coordinates are used. The default convergence criteria were used, namely 10⁻³ Hartree for the energy and 10⁻³ Hartree/Angstrom for the nuclear gradients. Solvent effects were taken into account for selected structures reported here, using the COSMO (Conductor like Screening Model) model of solvation, as implemented [15] in ADF. The type of cavity used was Esurf and the solvent used was CH₃CN (ε₀ = 37.5).
• (iii)OLYP/STO-TZ2P: The gga OLYP functional was applied, with the TZ2P basis set and COSMO solvent model, as implemented in the ADF 2018 package [14].
• (iv)OPBE0/STO-TZ2P: The hybrid OPBE0 functional was applied, with the TZ2P basis set and COSMO solvent model, as implemented in the ADF 2018 package [14].
• (v)B3LYP/STO-TZ2P: The hybrid B3LYP functional was applied, with the TZ2P basis set and COSMO solvent model, as implemented in the ADF 2018 package [14].

The [Ru(β-diketonato)₃] compounds were calculated as doublets (with S = ½) [11]. The input coordinates for the compounds were constructed using the program ChemCraft [16], and ChemCraft was also used to visualize the output files. The optimized coordinates, as well as an example input file, are provided in the supplementary information.

The DFT highest occupied molecular orbital (HOMO) and lowest unoccupied molecular orbital (LUMO) energies (E_HOMO and E_LUMO) were obtained from the output file of the DFT computations. These energies were used to further calculate both the electron affinity (EA) and ionization potential (IP) of each of the fourteen compounds, according to Koopman's theorem [17,18]:

$$\text{IP}=-E_{\text{HOMO}}$$

and

$$\text{EA}=-E_{\text{LUMO}}$$

The Mulliken electronegativity (χ) [19] [20] was computed for each compound, by application of the following formulae:

$$\chi =\left(\text{IP}+\text{EA}\right)/2$$

For the unsymmetrically substituted compounds 2 – 6 and 8 where R ≠ Rꞌ, an effective calculated energy (E_HOMO and E_LUMO) was determined by using the ratio of the relative population of the fac and mer isomers (n_i or n_j), as determined by the Boltzmann equation at T = 298.15 K:

$$\ln \frac{n_j}{n_i}=-\frac{\left(E_j-E_i\right)}{kT}$$

where n_i is the number of molecules with energy E_i (fac or mer in this case), with the Boltzmann's constant, k = 1.38066 × 10²³ JK⁻¹. E_i are provided in the supplementary information.