An Advanced Two-Step DNN-Based Framework for Arrhythmia Detection

Abstract

Heart arrhythmia is a severe heart problem. Automated heartbeat classification provides a cost-effective screening for heart arrhythmia and allows at-risk patients to receive timely treatments, which is a highly demanded but challenging task. Recent works have brought visible improvements to this area, but to identify the problematic supraventricular ectopic (S-type) heartbeats is still a bottleneck in most existing studies. This paper presents a two-step DNN-based framework to identify arrhythmia-related heartbeats. In the first step, a deep dual-channel convolutional neural network (DDCNN) is proposed to classify all heartbeat classes, except for the normal and S-type heartbeats. In the second stage, a central-towards LSTM supportive model (CLSM) is specially designed to distinguish S-type heartbeats from the normal ones. By processing heart rhythms in central-towards directions, CLSM learns and abstracts hidden temporal information between a heartbeat and its neighbors to reveal the deep differences between the two heartbeat types. As an improvement, we also propose a rule-based data augmentation method to solve the training data imbalance problem. The proposed framework is evaluated over three real-world ECG databases. The results show that our method outperforms the baselines in most evaluation metrics.

Introduction

Heart arrhythmia is known as abnormal heart rhythms, which threatens people’s lives by preventing their hearts from pumping enough blood into vital organs. It has been a major worldwide health problem for years, accounting for nearly of global deaths every year [13]. Early detection and timely treatment are the keys to survival from arrhythmia. The electrocardiogram (ECG) plays a pivotal role in arrhythmia diagnosis since it captures heart rate, rhythm, and vital information regarding the electrical heart activities and related conditions. However, the manual interpretation of ECG recordings is time-consuming and error-prone, especially for the long-term ECG recording which is essential to capture the sporadically occurred arrhythmia [17]. Therefore, an automated method to assist clinicians in detecting arrhythmia heartbeats from ECG is highly demanded.

Heartbeat classification on ECG is a core step towards identifying arrhythmia. As reported by the Association for Advancement of Medical Instrumentation (AAMI) [2], heartbeats can be categorized into five super classes: Normal (N), Supraventricular (S) ectopic, Ventricular (V) ectopic, Fusion (F) and Unknown (Q). In particular, problematic arrhythmias are mostly found in S-type and V-type heartbeats [6]. Figure 1 shows several ECG samples of different heartbeat types. We can see that the V-type heartbeat exhibits a huge morphological difference against other heartbeats, while the normal and the S-type heartbeats are similar in shape. It is less likely to accurately identify S-type heartbeats from normal ones merely based on morphology. In clinical practice, special rhythm information between two heartbeats, known as the RR-interval, is needed to help identify S-type heartbeats because S-type heartbeats are premature and they normally have shorter previous-RR-intervals than normal heartbeats. However, the inter- and intra-patients variations existing in the heart rhythms still impose great challenges to detection tasks. Besides, the sporadic occurrence of S-type heartbeats can also be an issue that tends to bias an automated heartbeat classification method.

Fig. 1.

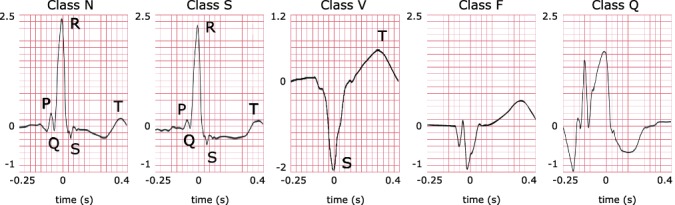
Examples of different types of heartbeats. Letters indicate the P-waves, R-peaks, QRS-complexes and T-waves, corresponding to their references in the medical literature. Time gap between two successive R peaks is known as RR-interval. Specifically, previous-RR-interval denotes the interval between the current R peak and the previous R peak. In comparison to the normal heartbeat (class N), the S-type heartbeat has a less obvious P-wave which is due to junctional premature beating. The V-type heartbeat exhibits a deep and capacious S-wave caused by left bundle branch block. Class F is a fusion of paced and normal heartbeats. The unclassifiable beat is denoted as class Q.

Existing solutions for the heartbeat classification problem mostly follow a traditional pattern recognition paradigm [4, 6, 14, 17], in which the fluctuations of the raw ECG signals are modeled by a set of carefully extracted features, such as RR-intervals, wavelet coefficients, and morphological amplitudes. However, pattern-based classification models often experience difficulties in achieving satisfactory performance on abnormal heartbeat detection, especially when S-type arrhythmia heartbeats are involved. Besides, the effectiveness of extracted features, the mutual-influences among features, and the compatibility between the feature distribution and the classifiers [5] are three major factors that lead to a solid upper-bound on model performance.

Recent advances in heartbeat classification are largely driven by deep neural networks (DNNs). In consideration of the sporadic occurrence of S-type heartbeats, which imposes a great challenge to DNN training, many DNN-based studies use synthetic heartbeats for model training and evaluation [1, 8, 9, 15, 16]. However, these efforts suffer from data leakage because, after augmentation, data is not partitioned patient-wise into training and test sets. So that beats from the same patient may appear in both training and test data. The deep learning algorithms may learn patient-specific characteristics during training and gain a nearly-perfect classification performance on test data. Additionally, the over-optimistic results obtained from data leakage have hided a potential limitation of these DNN models in which only the ECG segmented heartbeats are accepted as inputs. The inter-heartbeat rhythm information, like RR-intervals, is not well considered in these models. Without such information, a high misclassification rate is probably obtained on S-type heartbeats. The problem is still open.

Contributions: In this work, we propose a two-step deep neural network-based heartbeat classification framework. Due to the observed difficulty of detecting S-type heartbeats from N-type heartbeats, the proposed framework trains a deep dual-channel convolutional neural network (DDCNN) which accepts segmented heartbeats as input in the first step to classify V-type, F-type and Q-type heartbeats. At this stage, S-type and N-type heartbeats are not the targets, so they are put into one bundle to be studied in the next step. In the second step, a central-towards LSTM supportive model (CLSM) is specially designed to distinguish S-type heartbeats from N-type ones. The RR-intervals of a heartbeat and its neighbors are arranged in sequence form, serving as the input to CLSM. In particular, CLSM learns and extracts hidden temporal dependency between heartbeats by processing the input RR-interval sequence in central-towards directions. Instead of using raw individual RR-intervals, the abstractive, mutual-connected temporal information provides stronger and more stable support for identifying the problematic S-type heartbeats. Besides, as an improvement as well as a necessary driver for activating the CLSM, a rule-based data augmentation method is also proposed to supply high-quality synthetic samples for the under-represented S-type RR-interval sequences. To avoid data leakage, the benchmark dataset is split into training and test sets at patient level following the well-recognized inter-patient division paradigm proposed in [6]. The synthetic training samples are generated from the training set only.

The Proposed Framework for Arrhythmia Detection

The proposed framework consists of DDCNN and CLSM. DDCNN is used to capture the morphological patterns of heartbeats, and CLSM is specially designed to handle the temporal information between heartbeats. Details of these two models and the proposed data augmentation for driving CLSM are presented in this section.

Deep Dual-Channel Convolutional Neural Network

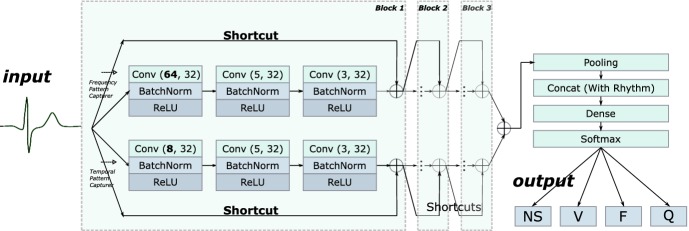
The architecture of DDCNN is presented in Fig. 2. The network accepts segmented ECG heartbeats (modified limb lead II, sampled at 360 Hz) as input, and outputs a prediction of probabilities of the N&S-bundle, V, F and Q classes. DDCNN is designed as a dual-channel convolutional neural network, with the small filter channel Conv(8, 32) capturing subtle fluctuations and the larger filter channel Conv(64, 32) handling wave patterns in ECG heartbeats. Information from the two channels are added together before the pooling operation. The entire DDCNN contains 18 convolutional layers, a pooling layer, a concat layer, a dense layer, and a softmax output layer. Specifically, the concat layer is designed to concatenate rhythm information (RR-intervals) to assist heartbeat classification. Each convolution operation is followed by a batch normalization and a ReLU activation. Every three convolutional layers of each channel are packed into a residual block and bypassed by a shortcut connection. The stacked residual blocks design reduces the network degradation risk and accelerate the training process.

Fig. 2.

Architecture of DDCNN, where Conv(x, y) denotes a convolutional layer with a kernel in size x and an output of y feature maps.

Central-Towards LSTM Supportive Model

The proposed CLSM consists of two specially designed central-towards LSTM layers and one softmax output layer. The term ‘central-towards’ means that information in an LSTM chain flows from farthermost units in both sides towards the central units, without crossing over with each other. A graphical representation of our model is provided in Fig. 3.

Fig. 3.

Central-towards LSTM Supportive Model architecture.

CLSM accepts heartbeats’ previous-RR-interval sequences as inputs. A previous-RR-interval sequence of the heartbeat 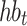is defined as

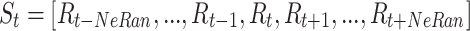1

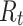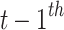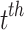where denotes the RR-interval between the and heartbeats, and NeRan defines the range of a heartbeat’s neighborhood. The default value of NeRan is 25. A previous-RR-interval sequence 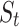is labeled as the same label of the central heartbeat 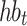, which is N-type or S-type.

Each central-toward LSTM layer contains 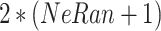common LSTM units. Particularly, the two central units receive and process the learned temporal dependencies from the previous and the posterior heartbeats, respectively.

Given an input sequence , update equations of a unit in the proposed central-toward LSTM layer depend on the unit’s position n at the layer, where . Let 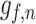, , 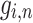, 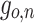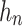denotes the forget gate, input gate, output gate, and the output of the unit, respectively.

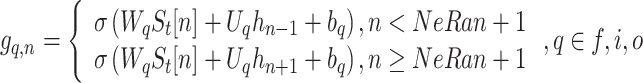2

where W and U are the weight matrix of inputs and recurrent connections, respectively, and b denotes the bias. We define the change of the memory as:

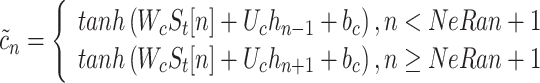3

Then the cell state is determined by the following equation:

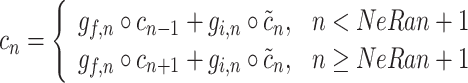4

The output of the unit depends on the cell state, which is given by:

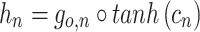5

In the central-toward LSTM layer, the central units output 32 feature maps in size 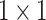. The feature maps are flattened before being processed by a softmax function for classification. The model outputs probabilities of the central heartbeat being normal and S-type.

Rule-Based Data Augmentation

The sporadic occurrence of the S-type heartbeats has resulted in a serious class imbalance problem in the benchmark training heartbeat data, which puts an obstacle to the successful training of CLSM. To generate synthetic samples for the under-represented S-type heartbeats becomes necessary and critical. Many oversampling techniques, such as SMOTE [3], have been introduced for data augmentation purpose, but these techniques are mainly designed for data samples that are represented by extracted features. Elements in a heartbeat’s previous-RR-interval sequence 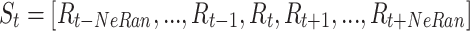have evident linear correlations, which are different from the mutual-independent features. Application of the existing oversampling methods will introduce invalid samples and make the training even worse.

To solve the problem, we propose a rule-based data augmentation method to generate synthetic previous-RR-sequences of the S-type heartbeats. Basically, a valid synthetic previous-RR-interval sequence subjects to 3 medical facts:

1. S-type heartbeats normally have shorter previous-RR-intervals than the normal ones. (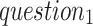: what is the valid range of distance between previous-RR-intervals of S-type and normal heartbeats?)

2. Heartbeats of the same type exhibit a limited variation in the previous-RR-intervals within a short period. (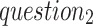: how much the variation is?)

3. Some normal heartbeats can be found within the neighborhood scope of a S-type beat. (: how many normal heartbeats can be found?)

The above medical facts provide a qualitative overview of what a valid synthetic sample should be. To synthesize a new valid sample, we still need to explicitly answer the questions following each medical fact.

The proposed method seeks for the answers via performing a statistical analysis on the benchmark training set (DS1 of MIT-BIH-AR [12]). We define three variables, gap, varPct and nAmt for questions 1, 2 and 3, respectively. Statistically, we have: ; ; 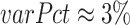and .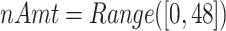

Let nVals and sVals be the collections of previous-RR-intervals of the normal and the S-type heartbeats in the training set, respectively. The proposed rule-based data augmentation method is detailedly illustrated in Algorithm 1.

By complying with the rules (line 3, 5, 8 & 11 in Algorithm 1) and creating new combinations (line 2, 4, 9 & 12 in Algorithm 1) from the existing data, our method is able to generate high-quality and diversified S-type training sequences.

Experimental Evaluation

Extensive experiments on three real-world ECG databases are implemented to evaluate the proposed framework and the rule-based data augmentation method. In this section, we introduce the databases and experiment settings, and then discuss the experimental results.

Arrhythmia Datasets

The real-world ECG datasets used in this study are: (1) MIT-BIH Arrhythmia database (MIT-BIH-AR); (2) MIT-BIH Supraventricular Arrhythmia database (MIT-BIH-SUP) and (3) St.-Petersburg Institute of Cardiological Technics 12-lead Arrhythmia database (INCART). The databases are all publicly available in the Physiobank [12].

MIT-BIH-AR is the benchmark database for arrhythmia detection, which is used in most published research [11]. To fairly compare against existing methods, we train and test our framework in this database following the well-recognized inter-patient evaluation paradigm [6]. MIT-BIH-SUP and INCART are used to demonstrate the generalizability of the proposed framework to external data.

• MIT-BIH-AR contains 48 two-lead ambulatory ECG recordings from 47 patients. The recordings were digitized at 360 Hz per second per channel with 11-bit resolution over a 10-mV range. For most of them, the first lead is modified limb lead II (except for the recording 114). The second lead is a pericardial lead. In this study, only the modified limb lead II is used.

• MIT-BIH-SUP consists of 78 two-leads recordings, with each of them approximately 30 min in length. The recordings are sampled at 128 Hz. They were chosen to supplement the examples of supraventricular arrhythmias in the MIT-BIH-AR database.

• INCART consists of 75 ECG recordings sampled at 257 Hz. Each recording contains 12 standard leads. Similarly, only the modified limb lead II is used in this study. Most of the recordings have ventricular ectopic heartbeats.

Experiment Setup

The experimental setup procedures are shown as follows.

• Benchmark Training and Test Datasets. We divide MIT-BIH-AR into a training and a test set at patient level following the well-recognized inter-patient evaluation scheme [6]. Table 1 presents the division in detail, where DS1 is the training set and DS2 in the test set.

• Heartbeats Segmentation. We segment each recording to heartbeats based on the R peak locations in notations. For each R peak, 70 samples (200-ms) before R peak and 100 samples (280-ms) after R peak were taken to represent a heartbeat. After segmentation, the heartbeat distributions of each dataset are shown in Table 2.

• Previous-RR-Interval Sequence Generation. For each segmented normal or S-type heartbeat 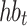, we generate a previous-RR-interval sequence 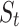correspondingly.

• Data Augmentation. We generate synthetic S-type previous-RR-interval sequences from the training set (DS1) using our rule-based data augmentation method. After data augmentation, the sequences for training CLSM are made up of 44738 normal and 45908 S-type sequences.

• Training Specification. Both the proposed DDCNN and CLSM are trained with a variant of the gradient decent algorithm named Adam [7]. The learning rate are set to 0.001 with no decay. The Categorical Cross-Entropy function is used to measure the loss.

• Evaluation Metrics. The evaluation metrics used in this study are accuracy (ACC), precision (PRE), recall (REC) and f1 score (F1).

Table 1.

The inter-patient division paradigm (for MIT-BIH-AR)

Dataset	Recordings
DS1	101, 106, 108, 109, 112, 114, 115, 116, 118, 119, 122, 124, 201, 203, 205, 207, 208, 209, 215, 220, 223, 230
DS2	100, 103, 105, 111, 113, 117, 121, 123, 200, 202, 210, 212, 213, 214, 219, 221, 222, 228, 231, 232, 233, 234

Recordings 102, 104, 107 and 217 containing paced beats are excluded [2].

Table 2.

Heartbeat distributions in MIT-BIH-AR, MIT-BIH-SUP and INCART

Database	N	S	V	F	Q
DS1	45808	943	3786	414	8
DS2	44198	1836	3219	388	7
MIT-BIH-SUP	158760	11976	9718	23	76
INCART	150210	1917	19621	218	6

: Overall Heartbeat Classification

In this section, we evaluate the heartbeat classification performance of the proposed framework on the benchmark database and compare the results against multiple baseline algorithms [1, 4, 6, 10, 14, 17] derived from literature. Table 3 summarizes the comparative results. The comparison focuses on normal, S-type and V-type heartbeats because, according to the AAMI standard [6], F-type and Q-type heartbeats are naturally unclassifiable and penalties should not be applied for the misclassification of these heartbeats. The proposed DDCNN + CLSM architecture performs significantly better than the baseline algorithms on the overall accuracy (95.1% vs 78.0%–93.1%), F1 score of normal heartbeats (97.6% vs 87.3%–96.9%), recall rate of S-type heartbeats (83.8% vs 29.5%–76.0%), precision rate of S-type heartbeats (59.4% vs 36.0%–52.3%), and F1 score of S-type heartbeats (69.5% vs 33.4%–56.3%). The performance on V-type beats is above the average, ranking the place of the listed works.

Table 3.

Performance comparison on DS2 of MIT-BIH-AR

Method	ACC	N			S			V
		REC	PRE	F1	REC	PRE	F1	REC	PRE	F1
DDCNN + CLSM	95.1	97.5	97.6	97.6	83.8	59.4	69.5	80.4	90.2	85.0
DDCNN Only	93.4	97.9	95.7	96.7	13.2	20.7	16.1	87.2	87.7	87.5
DDCNN Only (without Concat)	85.9	90.2	95.9	93.0	3.9	3.5	3.7	82.4	46.3	59.2
Acharya [1]	71.3	73.3	95.0	82.6	6.3	2.3	3.4	90.8	28.2	43.5
De Chazal [6]	81.9	86.9	99.2	92.6	75.9	38.5	51.1	77.7	81.9	80.0
Ye [14]	86.4	88.5	97.5	92.8	60.8	52.3	56.3	81.5	63.1	71.2
Zhang [17]	86.7	88.9	99.0	93.7	79.1	36.0	49.5	85.5	92.8	89.0
Shan [4]	93.1	98.4	95.4	96.9	29.5	38.4	33.4	70.8	85.1	77.3
Mariano [10]	78.0	78.0	99.1	87.3	76.0	41.0	53.3	83.0	88.0	85.4

Results in this table are presented in percentage (%), which are obtained on DS2 of MIT-BIH-AR following the same evaluation procedures.

It is apparent from Table 3 that most of the listed works struggle in the detection of S-type heartbeats. We re-implement the DNN model [1] and evaluate it following the inter-patient paradigm. The result confirms that, without considerations of heart rhythm, a DNN is less likely to identify S-type heartbeats. Zhang et al. [17] and Mariano et al. [10] achieve close recall rates of S-type heartbeats as our framework, but they sacrifice S-type heartbeats precision rates (36.0% and 41%, respectively) and normal heartbeats recall rates (88.9% and 78.0%, respectively). This implies that both these two works misclassify a large portion of normal heartbeats as S-type heartbeats. In clinical practice, the erroneous misclassification of normal heartbeats as disease heartbeats leads to unnecessary additional tests, unnecessary patient treatments, expensive costs, and risks for patients.

An ablative analysis is also performed. We remove CLSM from the proposed framework and use standalone DDCNN for overall classification of all five types of heartbeats. The result is shown as DDCNN Only in Table 3. To further investigate whether raw RR-intervals help to identify problematic heartbeats, we train a DDCNN without the concat layer for comparison. The result is denoted as DDCNN Only (without Concat). It is clear that, without the proposed CLSM, both standalone DDCNNs can hardly detect S-type heartbeats. The DDCNN with the concat layer performs better on both S-type and V-type heartbeats than the DDCNN without the concat layer. The outcome indicates that RR-intervals help to identify problematic heartbeats, especially for S-type heartbeats, but the assistance of raw RR-intervals is limited because they are likely to be influenced by the intra- and inter-patients variations. Therefore, having a consideration of neighbor heartbeats and performing an abstraction of the temporal dependency from the raw RR-intervals is necessary.

: Generalization of the Proposed Framework

We apply the proposed framework (trained in DS1) to MIT-BIH-SUP and INCART to demonstrate its generalizability. To be fitted, ECG recordings in these two databases are re-sampled to 360 Hz. Table 4 summarizes the results.

Table 4.

Generalization performances (%) on MIT-BIH-SUP and INCART

Method	Dataset	ACC	N		S		V
			REC	PRE	REC	PRE	REC	PRE
Proposed	MIT-BIH-SUP	88.2	90.6	97.8	72.6	53.5	70.0	43.0
Proposed	INCART	91.6	92.0	99.6	81.0	14.4	91.0	81.9
Mariano L [10]	INCART	91.0	92.0	99.0	85.0	11.0	82.0	88.0

To the best of our knowledge, this work is the first one to report heartbeat classification results on MIT-BIH-SUP. When being applied on MIT-BIH-SUP, the proposed framework experiences a slight performance drop on V-type heartbeats detection. However, this is mainly due to the low-resolutions of the source ECG recordings which are originally sampled at 128 Hz.

We compare the proposed framework to Mariano’s work [10] on INCART. Mariano’s work is one of the few works that conduct model evaluation on both MIT-BIH-AR and INCART. The results show that both works achieve promising performances, where the proposed framework slightly outperform Mariano’s work [10] in majority metrics. The commonly low precision rates of S-type heartbeats are mainly due to the extreme class imbalance of INCART.

: Rule-Based Data Augmentation Versus SMOTE

We investigate the effectiveness of our rule-based data augmentation method in this section. The SMOTE algorithm [3] is used as a baseline. We train individual CLSMs with the rule-based augmented sequences and the SMOTE augmented sequences, respectively, and evaluate their classification performances using all normal and S-type heartbeats in DS2. Table 5 summarizes the results.

Table 5.

The impact of data augmentation method on CLSM’s performance

Method	ACC()	N		S
		REC()	PRE()	REC()	PRE()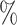
CLSM + Rule-based Method	97.7	98.2	99.4	85.6	65.7
CLSM + SMOTE	94.7	97.7	96.8	19.6	25.5

Apparently, SMOTE failed to generate valid previous-RR-interval sequences for training the proposed CLSM. The CLSM trained with SOMTE-generated samples couldn’t effectively identify S-type heartbeats, with both the recall and precision rates being lower than 30%. The poor result is not surprising because the SMOTE method is designed for featurized data oversampling. Thus, data like previous-RR-interval sequences with internal connections between elements will disable the SMOTE method. By contrast, using the medical rules as a guide, the proposed rule-based data augmentation method can generate high-quality synthetic sequences that reflect the true distribution of the real-world data to support the CLSM.

Discussion

Experimental results achieved on the three real-world ECG databases have proven the effectiveness and the robustness of the proposed framework and indicated that the proposed framework has the potential to make a substantial clinical impact. In particular, the proposed CLSM structure distinguishes our framework from the others. It provides a promising solution for separating S-type heartbeats from normal heartbeats which is one of the most problematic tasks for existing arrhythmia detection methods.

While CLSM has provided a novel idea of how to incorporate heart rhythm to help individual heartbeat classification, we have also implemented experiments to investigate how the input neighborhood range, NeRan, influence CLSM’s performance. The default value for NeRan is 25. In our experiment, we try different NeRan values from 2 to 35. The results show a growing trend of CLSM performance with NeRan increasing from 2 to 16. CLSM stably maintains in its optimal performance when NeRan is greater than 20. This means an input previous-RR-interval sequence of approximately 35 s is the minimum requirement for CLSM to accurately capture useful information from heart rhythm.

Although CLSM is initially designed as the second-step structure in the proposed framework, it is a general and flexible binary classifier. For those works suffering from the confusion of S-type and normal heartbeats, CLSM can be easily integrated as a complement without changing their original structures. This is why we define CLSM as a supportive model.

Conclusion

This work presents a two-step DNN-based classification framework to identify arrhythmia-related heartbeats from ECG recordings. The framework consists of a deep dual-channel convolutional neural network (DDCNN) and a central-towards LSTM supportive model (CLSM). In step-1, DDCNN incorporates both temporal and frequent patterns to identify V, F and Q-type heartbeats. In step-2, CLSM distinguishes S-type heartbeats from normal ones by taking advantage of the central-towards LSTMs to learn and abstract hidden temporal information of each heartbeat. The experimental results obtained on three real-world databases show that the proposed framework has the potential to make a substantial clinical impact.