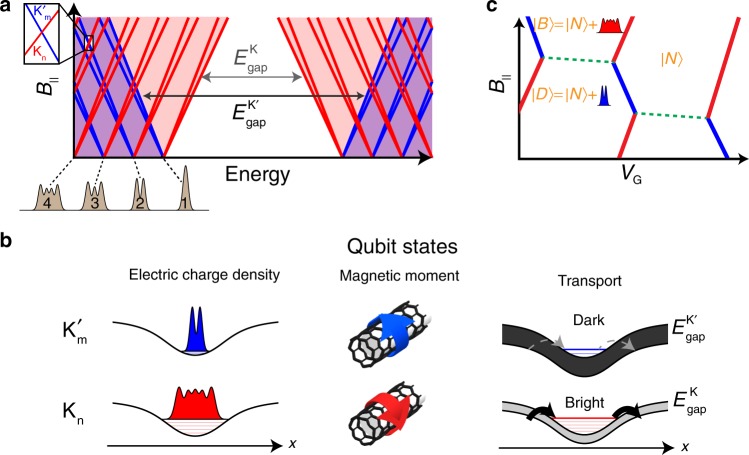
Fig. 1. A qubit based on the natural wavefunctions in a carbon nanotube.

a Single particle energy spectrum of a single quantum dot in a carbon nanotube, as a function of magnetic field parallel to the tube axis, B_||. Each spatial wavefunction (gray illustrations, bottom) has at B_|| = 0 a 4-fold spin (↑, ↓) and valley (K−red, K′−blue) degeneracy, which is lifted at finite B_|| with slopes given by the spin and orbital magnetic moments ±μ_spin ±μ_valley. B_|| also modifies the bandgap of the two valleys: $E_{\mathrm{gap}}^{\mathrm{K}}$ decreases and $E_{\mathrm{gap}}^{{\mathrm{K}}^{\prime }}$ increases with B_|| (gray arrows). The intersection of two levels at finite B_|| (inset) is used as the basis of our qubit. b The two intersecting levels (referred to as K_n, $K_{\mathrm{m}}^{\prime }$) differ in three quantities: Since the K_n state is a much higher bound state in the confinement potential than the $K_{\mathrm{m}}^{\prime }$ state, it is spread more along the nanotube (left). The K_n and $K_{\mathrm{m}}^{\prime }$ states originate from opposite valleys with opposite magnetic moments due to opposite directions of electron motion around the nanotube circumference (center). The barriers of the dot are formed by the nanotube bandgap, which at finite B_|| is different for the two valleys (see panel a), making the tunneling from the leads into the K_n state much faster than to the $K_{\mathrm{m}}^{\prime }$ state (bright/dark, right panel). c Charge stability diagram, obtained by adding the charging energy to the energy spectrum in the inset in panel a. Coulomb blockade peaks zig-zag between charging of the two valleys (red/blue). The triple point used in the experiment is between the $∣N⟩$ state, having N holes, and the $∣D⟩$ and $∣B⟩$ states, which are obtained by adding either a K_n hole (red) or a $K_{\mathrm{m}}^{\prime }$ hole (blue).